基于脉冲序列重构的雷达PRI调制类型智能识别算法研究

黄中瑞 唐 波

（国防科技大学电子对抗学院，安徽合肥 230037）

1 引言

雷达脉冲重复间隔（PRI）是雷达信号的关键参数，对于雷达性能发挥起着至关重要的作用［1-2］。不同工作场景下，雷达PRI的变化规律差异巨大，为了实现特定功能，通常需要对雷达PRI 的调制类型进行特殊设计，因此分析雷达PRI 的调制类型是电子对抗领域非常重要的研究内容［3-5］。与雷达工作频率、脉冲宽度等信号参数不同的是：雷达PRI变化范围广、调制类型多、受环境因素影响大，这给相应的分析工作带来了巨大挑战。目前，常用的PRI 调制类型分析方法有：直方图法、到达时间差（ΤDOA）分析法、特征提取分析法、人工智能分析法等，下面对几种比较经典的分析方法概述如下。

直方图法是雷达PRI 调制类型最早的分析方法，由于分析过程严重依赖人工介入，因此该方法的识别效率比较低，而且识别结果也因人而异。基于ΤDOA 矩阵分析的PRI 调制类型识别方法［6-7］，能够实现PRI 调制类型的自动识别，而且能够估算特定时间段少量脉冲的丢失数目和具体位置。但该方法的适用性比较差，目前仅能应用于PRI 固定、PRI 参差等特殊调制类型。基于特征提取的PRI调制类型识别方法［8-10］，主要根据PRI的具体变化规律提取典型值数目、标准差均值比、连续性参数、sp 曲线等特征，然后利用决策树、支持向量机等分类器完成PRI调制类型的识别。然而，这些方法仍然存在识别PRI调制类型少，对脉冲丢失率的稳健性差等问题。

传统方法在识别PRI 调制类型时，主要是以PRI 值为对象进行分析，开展异常值剔除、丢失PRI填补等处理，这些方法对PRI值的矫正能力有限，无法准确还原PRI 的真实变化规律，致使PRI 调制类型的识别性能下降。与具体PRI 值相比，雷达PRI的调制周期是一个显著特征，利用其开展PRI 变化规律挖掘将更有利于提升PRI调制类型的识别准确率［11-12］。文献［12］基于频繁ΤDOA 集的抽取和扩展，并结合脉宽信息实现了PRI周期样本图重构，为PRI调制类型识别提供了有利基础。然而该方法对于单个周期内存在多个相同PRI典型值的调制类型重构能力有限，因而在PRI 排定或者PRI 驻留等类型的分析上效果较差。

随着人工智能技术的不断发展，特别是深度学习技术在语音识别、图像分析等领域的成功应用，越来越多的学者尝试将深度学习技术迁移到电磁数据分析中，开展了基于卷积神经网络（CNN）、深度神经网络（DNN）等的PRI 调制类型识别算法研究［13-19］。这类方法无须人工提取特征，能够直接完成从数据到结果的一体化识别任务，而且对干扰脉冲、脉冲丢失具有很强的容忍性。但是基于深度学习技术的PRI 调制类型识别也存在一定的不足，比如对数据长度有严格要求，常用的数据长度规整处理容易破坏实际PRI 内在的调制规律，影响网络的识别效果。另外，这类方法对数据量有较为严格的要求，只有获得足够的数据才能避免具体环境对PRI调制类型识别结果的影响。

为解决上述方法的不足，本文提出了一种基于脉冲序列重构的雷达PRI 调制类型智能识别算法，主要包括两部分工作：首先，利用PRI调制周期估计完成脉冲样本序列的重构，由于PRI 调制类型（PRI抖动除外）具有周期重复性，因此该措施能够有效减弱干扰脉冲，特别是脉冲丢失的影响；其次，利用CNN 完成PRI 调制类型的端到端识别，该方法能够减弱人工提取特征的局限性，不仅可以获取PRI 序列的深层特征，而且具有更强的环境适用性。

2 PRI调制类型基础

随着雷达多功能技术的不断发展，其PRI 调制样式也越来越复杂。目前，常见的PRI 调制类型包括：固定、抖动、参差、排定、滑变、驻留、正弦7种，下面对其进行简要阐述。

PRI 固定是指雷达在一段工作时间内，其信号的PRI 保持不变，该调制方式是雷达最为基本的信号形式，几乎所有雷达都会采用此种工作方式。PRI 抖动是指雷达PRI 在一个较窄的范围内快速、随机变化，变化范围通常为中心值的5%～10%，PRI抖动不具周期性，可提升雷达对近距离多目标的探测性能。PRI参差是指雷达发射信号采用若干个顺序排列的PRI，排列顺序一般固定不变，并且这些PRI具有周期重复性，PRI参差主要用于运动目标的检测。通常来讲，一个重复周期内PRI 的数值各不相同，而且参差数目一般不超过8。PRI排定是指雷达信号PRI 的多个值周期性地变化，变化规律与PRI 参差类似。与PRI 参差的区别是：一、单个周期内允许PRI的部分值重复；二、单个周期内PRI值的数目一般大于8。PRI 滑变是指雷达信号的PRI 在两个极值之间周期性地连续变化，根据具体的变化规律不同，PRI 滑变包括单向单滑、单向双滑、双向单滑、双向双滑4 种类型，本文主要考虑单向单滑。PRI滑变最主要的特点是相邻PRI（除变化端点外的PRI）的差值固定不变。PRI滑变主要用于消除目标遮蔽以及对恒定高度目标的覆盖。PRI正弦是指雷达信号的PRI在两个极值之间呈正弦周期变化，PRI正弦可以避免目标遮蔽，通常用于导弹制导或者炮火瞄准等。PRI 驻留是指雷达PRI 在某个数值上工作一段时间后又转到另一个数值，PRI 驻留是脉冲多普勒雷达主要采用的信号形式，PRI 驻留可以有效解决目标的距离模糊和速度模糊问题。

备注：一、PRI调制类型的示意图如图1所示；二、关于PRI调制类型更为详细的描述，特别是关于应用场景和性能分析等方面的内容请参考文献［20］。

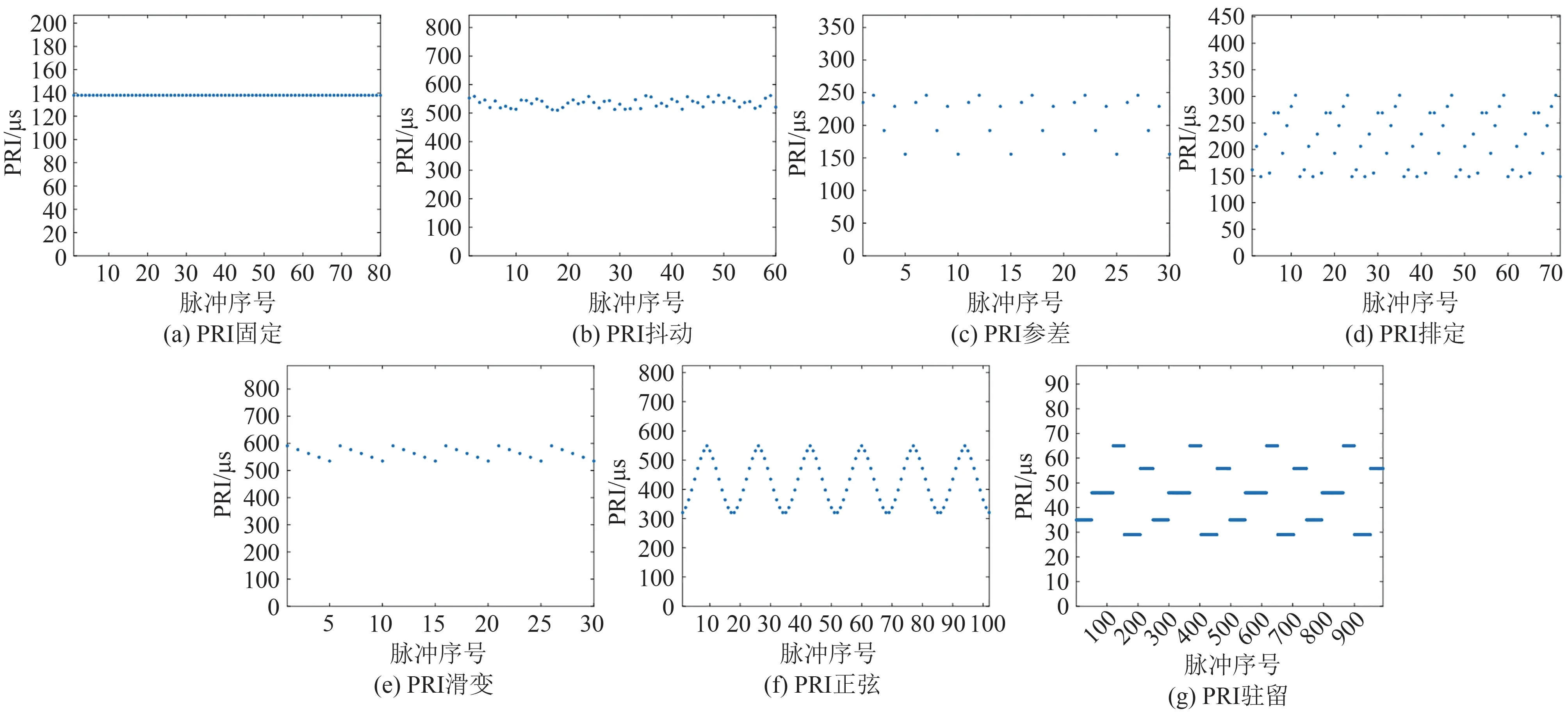
图1 PRI调制类型示意图Fig.1 Schematic diagrams of PRI modulation types

3 脉冲序列重构

由于环境干扰、装备性能、人为操作等各方面因素的影响，实际接收脉冲序列不可避免的会面临干扰脉冲、脉冲丢失、PRI 测量误差等问题。为提升PRI分析性能，需要对接收脉冲序列进行一定的预处理，关于干扰的预处理可以参考文献［10，18］，针对PRI丢失和PRI测量误差的处理，本文提出的脉冲序列重构算法能够进行很好地解决，主要包括：到达时间（ΤOA）多阶差分序列构造、基于直方图统计的PRI调制周期估计和脉冲序列构建三部分内容。

3.1 TOA多阶差分序列构造

假设接收脉冲序列的ΤOA为{tn}，n=1，2，…，N，则可以构造ΤOA的多阶差分序列如下：

其中，l表示ΤOA 的差分阶数。由于PRI 调制的周期性（PRI抖动除外），PRI调制周期及其各次谐波将会成为一个显著特征，并且对脉冲丢失具有较强的稳健性。

3.2 基于直方图统计的PRI调制周期估计

本部分在3.1节的基础上，对PRI调制周期或者是其谐波进行估计，为后续的脉冲序列构建提供支撑。需要说明的是：由于所提方法能够对脉冲序列进行重新构建，因此本部分并不需要解决PRI调制周期估算的模糊性问题，这将大大降低算法的计算复杂度。

首先，将原始多阶差分序列按照升序原则进行排列，并将新的序列定义为表示重排序列的最小值和最大值；其次，以为起点，ΔT为离散化间隔（一般设置为ΤOA 测量误差γ的倍数，本文设置为2 μs），在时间长度上划分K个间隔，每个间隔的时间起点记为，k=1，2，…，K，每个间隔为左闭右开，其中；最后，定义一个K×2维的特征矩阵C，第一列为各个统计区间DΤOA 的均值，第二列为各个统计区间DΤOA的数目，具体数学模型如下：

其中，dk为临时变量，M为DΤOA典型值的数目。

由于离散化统计和测量误差等因素的影响，部分属于同一区间的DΤOA 典型值会被强制的分隔在不同的统计区间，因此需要对特征矩阵进行C修正，具体方法为：如果两个区间的均值差小于0.7ΔT，则将两个区间的均值和数目进行合并处理，

根据式（4）可以获得PRI调制周期PRItotal为：

其中，K′为DΤOA 统计区间合并后的实际数目，PRItotal=0说明原始的PRI序列不具周期性。

3.3 脉冲序列构建

本部分主要完成脉冲序列的重构，令CNN所需的PRI 数目为N′，主要分为两种情况对脉冲序列的构建进行说明。

3.3.1 原始脉冲序列不具周期性

对于上文提到的7 种PRI 调制类型而言，只有PRI抖动不具调制周期性。如果采用简单的截断或者扩充方法对脉冲序列进行构建，无法解决脉冲丢失带来的谐波问题，从而造成PRI 抖动变化与PRI驻留变化特征类似，使得CNN 识别性能下降。为此，本部分利用PRI抖动的变化特性，对其脉冲序列进行重构，具体方法如下。

首先，利用PRI分布的高斯特征将部分非常规异常值进行剔除。计算原始PRI序列的均值和标准差，

其次，利用3.2 节的直方图统计方法对异常值剔除后的PRI进行统计分析，需要说明的是，考虑到抖动调制类型的PRI 值变化比较剧烈，此处的离散化间隔ΔT′=100γ。分析PRI 统计区间的典型值数目，将最大值区间内对应的原始PRI 序列挑选出来作为样本基序列，记为{PRI1，PRI2，…，PRIP}，P为该集合内PRI值的数目。

再次，根据样本基序列构建脉冲序列。判断样本基序列内所有PRI的数目P与CNN输入所需的N′之间的关系，如果P≥N′，则直接选取前N′个PRI 值送入网络进行训练或者识别。如果N′>P，则利用样本基序列的统计特性重构样本序列，具体方法如下：

计算样本基序列的均值和标准差，

最后，利用式（7）采用高斯随机序列产生方法，构造N′个均值和标准差符合式（7）的脉冲序列。

3.3.2 原始脉冲序列具有周期性

首先，将整个脉冲序列的ΤOA 以PRItotal为周期进行切分，构造调制周期ΤOA 集合{qn}，具体如式（8）所示：

其中，mod(·，·)表示求余运算。

然后，利用3.2节的思想对集合{qn}的值进行直方图统计分析，与3.2 节不同的是，此处需要对个别异常值进行删除处理，具体准则为：若某个统计区间内ΤOA的数量满足式（9）则将小该统计区间内所有的ΤOA值删除，

其中，K″为统计区间的数目，η为人工参数，一般设置为0.3，此处的C2，k代表的是脉冲ΤOA的数目。

最后，判断调制周期内所有PRI 的数目M′与CNN 输入所需的N′之间的关系，如果M′≥N′，则直接选取前N′个PRI 值送入网络进行训练或者识别。如果N′>M′，则将调制周期内的PRI 进行周期性填充，直至填充数目与N′相等即可。

4 基于CNN的PRI调制类型识别

CNN是深度神经网络的一种特殊网络，该网络在图像识别以及语音识别等领域得到了广泛应用，本文在现有CNN研究的基础上，构造一种适用于一维时序信号的网络结构，以期提升雷达PRI 调制类型的识别准确率。

数据预处理：为了避免数值的绝对大小对网络的影响，同时突显信号的差异性，本文的预处理操作主要是去均值，具体为：

CNN 网络设计：本文所设计的CNN 网络结构主要包括：卷积层、池化层、批规范化以及激活函数等，这里对主要的网络层和参数进行简要阐述，具体如下。

卷积层是CNN的基础操作，主要通过局部感受视野提取时域信号的短时特征，通过平移操作获得时域信号的全局特征（对应于下一层不同的神经元），相比于传统的全连接层，卷积层能够共享权值和偏置，大大减小了网络所需优化变量的数目，不仅能够减缓过拟合的风险，而且更有利于扩展网络的深度，提升网络的性能。本文所用的卷积核主要包括3种：20×1、15×1和10×1。

池化层实质上是一种“降采样”操作，通过池化操作将某个局部区域的压缩显著特征提取出来，本文主要采用最大池化，具体的池化视野为2×1。

批规范化操作是对每次批处理的样本进行规范化操作，具体包括四步：一、求解批处理数据的均值；二、求解批处理数据的方差；三、利用均值和方差对数据进行标准化处理；四、对标准化后的数据加入尺度因子和偏移，以还原初始数据的分布，保持网络的容量。批规范化操作能够减缓“梯度弥散”问题，提升网络的收敛速度。

激活函数是一种非线性变换，是增加网络表达能力的关键所在，目前常用的激活函数有：Sigmoid函数、tanh函数、修正线性单元（ReLU）、Leaky ReLU等，本文主要采用ReLU作为网络的激活函数。

Softmax 层主要用于将网络输出层的数值进行归一化处理，将输出值转化为概率值，为后续的信号分类提供基础。

目标函数是整个神经网络的“指挥棒”，是计算预测结果与真实标签之间误差的基本依据，也是反向更新网络权值和偏置的基础，本文主要采用交叉熵损失函数作为网络的目标函数。

本文设计的CNN网络结构如图2所示。

图2 CNN结构图Fig.2 Structural diagram of CNN

5 仿真分析

为说明所提方法的有效性，本部分以不同脉冲丢失率下的识别准确率为指标，对比分析本文算法、传统数据的CNN智能识别方法和文献［9］的具体性能。为了模拟仿真实际环境，设置干扰脉冲占比10%，脉冲丢失率为0%～80%，其中脉冲丢失率的离散化点数为9，直方图统计的PRI离散化间隔为2 μs，ΤOA测量误差γ为0.2 μs，数据模拟和网络训练均使用MAΤLAB完成，数据产生和网络参数设置如下。

（1）模拟数据产生

PRI 抖动：PRI 中心值在100～2000 μs 之间随机产生，每个PRI 值的抖动范围在10%以内，每次产生样本的长度为2000；PRI 正弦：幅度变化范围在120～200 μs 之间随机产生，均值在1.5 倍幅度范围-2000 μs 之间随机产生，每个周期内共有17 个PRI值，每次产生样本的周期数目为150；PRI 滑变：PRI变化间隔在4～50 μs 之间随机产生，均值在100～2000 μs 之间随机产生，一个周期内的PRI 数目在8～20 之间随机产生，每次产生样本的周期数目为200；PRI 固定：PRI 典型值在100～2000 μs 之间随机产生，每次产生样本的长度为2000；PRI参差：PRI差值在4～100 μs之间随机产生，均值在100～2000 μs之间随机产生，一个周期内的PRI 数目在2～7 之间随机产生，每次产生样本的周期数目为260；PRI驻留：PRI 差值在4～100 μs 之间随机产生，均值在300～400 μs 之间随机产生，PRI 典型值的数目在5～10 之间随机产生，单个周期内每个典型值的数目在60～70 之间随机产生，每次产生样本的周期数目为10；PRI 排定：PRI 差值在4～100 μs 之间随机产生，均值在100～2000 μs 之间随机产生，一个周期内的PRI数目在8～32之间随机产生，每次产生样本的周期数目为200。上述所有变化类型的模拟数据，每个丢失率下产生样本2000 个，共计18000 个，所有调制类型的样本总数为126000。

（2）CNN网络参数设置

输入样本长度为N′=1000 个PRI 值（即1001 个ΤOA），训练方法采用动量随机梯度下降方法，初始化学习率为0.001，每3 轮调整一次学习率，调整因子为0.5，批量样本规模为512，每20 次内部迭代验证一次训练准确率，最大训练轮数为10。总样本按照0.85 和0.15 的比例分为训练集和测试集，训练集按照0.85 和0.15 的比例分为训练数据和验证数据，每次训练都需对训练样本进行随机打乱操作。训练时采用脉冲丢失率0%～50%所含的样本构建训练集，测试采用脉冲丢失率0%～80%的样本对CNN的PRI调制类型识别准确率进行分析。

5.1 有效性验证

假设脉冲序列中存在的干扰脉冲数目占比为10%，脉冲丢失率为50%。

图3 为所提方法的CNN 训练过程，从中可知所设计网络在很少的迭代次数就能完成收敛，基本上在第一轮训练结束后就已经接近收敛，CNN的训练准确率为99.22%，验证准确率为99.21%，这说明整个训练过程中并没有出现过拟合现象，这一点在图3中也可以看出。

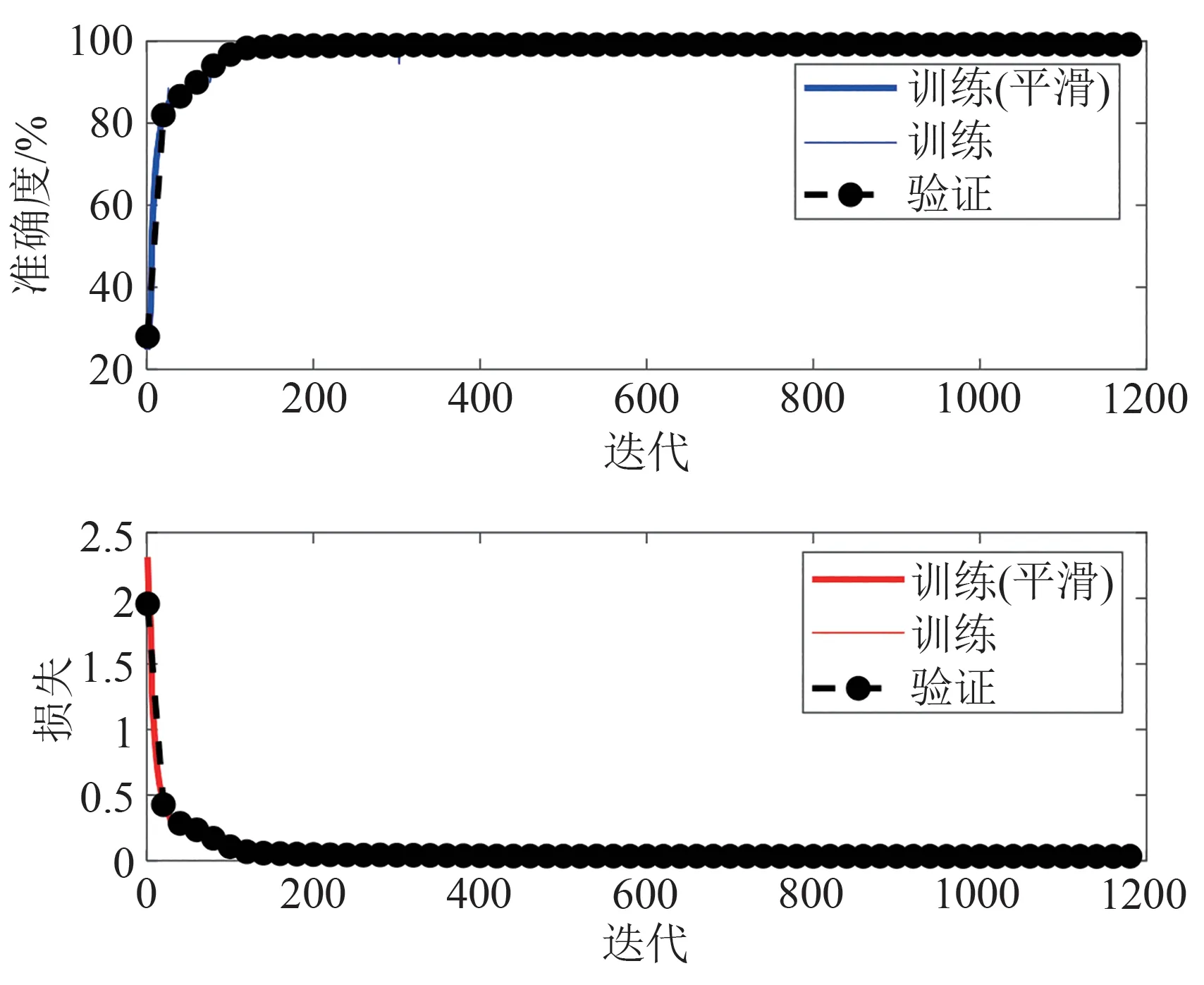
图3 网络的训练过程Fig.3 Network training process

表1 给出了PRI 调制类型的识别结果。从中可以看出，原始脉冲序列虽然受到了干扰脉冲、脉冲丢失（50%的丢失率）等非理想因素的影响，所提方法仍能实现PRI 调制类型的高精度识别，其中PRI排定的识别准确率最低为97.33%，其余调制类型的识别准确率均在99%附近。因此，所提方法对于PRI调制类型识别具有良好的优越性。

表1 PRI调制类型识别结果Tab.1 PRI modulation-type recognition results

5.2 稳健性验证

为了进一步说明本文方法的稳健性，分析PRI调制类型识别准确率随脉冲丢失率的变化，脉冲丢失率范围为[0，0.8]，离散化间隔为0.1，共计9 个点，其余仿真条件不变。为说明方法的有效性，将本文方法（简记为R-CNN）、文献［9］方法以及不对数据进行任何预处理直接对CNN 进行训练的识别方法（简记为CNN）进行对比分析。

图4 为PRI 调制类型识别准确率随脉冲丢失率的变化，在脉冲丢失率小于60%时，所提方法对于所有PRI 调制类型的识别准确率均在92%以上，平均识别准确率大于98%，在脉冲丢失率小于80%时，平均识别准确率在81%以上。文献［9］方法在脉冲丢失率小于40%时，PRI 调制类型的平均识别准确率为89%，在脉冲丢失率超过50%后，PRI调制类型的识别准确率急剧下降；另外，需要说明的是，文献［9］方法仅适用于PRI 抖动、PRI 滑变、PRI 固定、PRI 参差和PRI 驻留5 种变化类型，而本文所提方法适用于目前常见的7种变化类型。不对数据进行预处理，直接将其送入CNN 进行训练，获得的深度网络在PRI 调制类型识别上性能极差，几乎不可用。主要原因是：受干扰和脉冲丢失影响，PRI序列的变化特性出现了一定程度的“畸变”，要想提高CNN 性能，除了采用本文所提方法外，还可采用增大每种情况下的样本数量，让网络从海量数据中提取PRI 调制类型的“本质”特征，但是这种方法相比本文方法的性能仍有逊色。

图4 PRI调制类型识别准确率随脉冲丢失率的变化Fig.4 Recognition accuracy for PRI modulation type versus pulse missing rate

综上，所提方法在PRI 调制类型识别上具有综合的性能最优，分析原因：一方面，所提的基于CNN的PRI调制类型识别方法，无须人工提取特征，通过网络获取PRI 调制类型的“深度特征”，对环境具有更强的适应性；另一方面，本文所提的脉冲序列重构方法，较好地抑制了干扰脉冲，特别是脉冲丢失对PRI 调制规律的影响，精准的还原了PRI 序列变化特征的本貌，给CNN训练提供了高质量的样本数据，有效地提升CNN的识别性能。为说明本文所提脉冲序列重构的有效性，图5 和图6 给出了重构后的PRI序列和原始PRI序列。

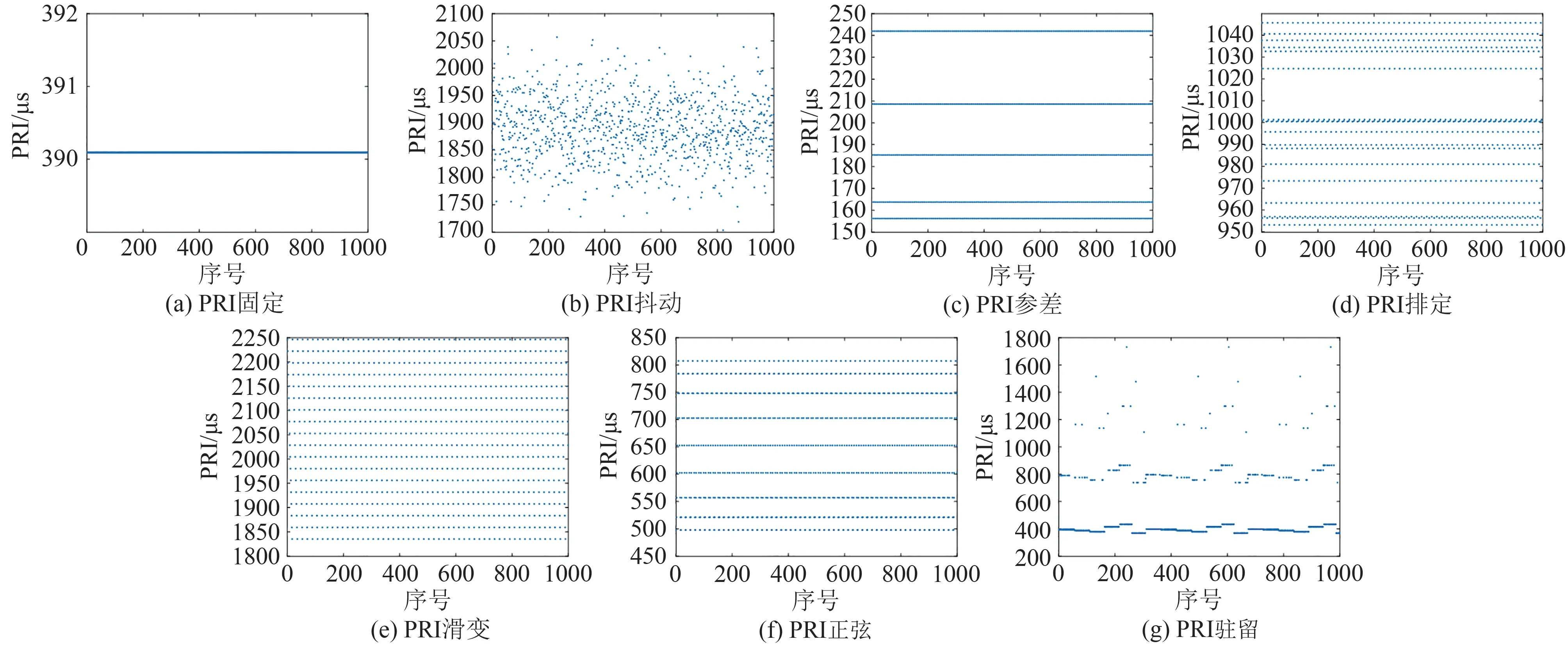
图5 重构的PRI序列Fig.5 Reconstruction of the PRI sequence

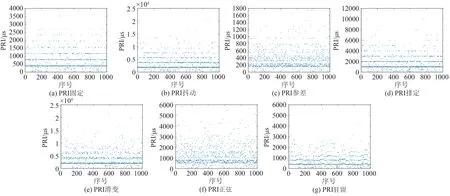
图6 原始的PRI序列Fig.6 Original PRI sequence

图5 和图6 给出了脉冲丢失率为50%时，重构后的PRI 序列和原始的PRI 序列。从中可以看出，采用所提方法进行重构，基本上能够消除脉冲丢失对PRI 调制规律的影响，快速获取PRI 的“本质”变化规律，这也是为什么R-CNN的识别性能要远优于CNN的原因。

另外需要说明的是，随着脉冲丢失率的不断增加，所有方法的PRI调制识别准确率都在不断下降，主要原因是：PRI 调制类型定义的基础是单个调制周期内（PRI抖动暂认定为调制周期为无限大）所有PRI数值的相对关系，随着脉冲丢失率的不断增大，单个周期内PRI 值的缺失也就越多，相对的变化关系也就越紊乱，最终导致PRI 调制类型的识别准确率不断下降。

6 结论

雷达PRI调制类型识别是雷达信号参数分析的重要组成部分，是提取雷达信号样式的基础，更是研判雷达型号甚至是雷达个体的重要支撑。为解决现有方法对于PRI 调制类型识别能力弱、受脉冲丢失影响大的不足，本文研究了一种基于脉冲序列重构的雷达PRI 调制类型智能识别算法。首先，区分PRI 调制是否具有周期性，提出了两种脉冲序列重构方法；然后，采用CNN 实现了PRI 调制类型的智能识别；最后，通过仿真分析表明了所提方法的有效性，在脉冲丢失率小于60%时，所提方法对于所有PRI 调制类型的识别准确率均在92%以上，平均识别准确率大于98%，在脉冲丢失率小于80%时，平均识别准确率在81%以上。然而，所提方法主要适用于单辐射源信号的PRI 分析，考虑到实际环境的复杂性，研究具备多源PRI 分选和调制类型识别的一体化智能分析方法将是后续研究的重点。