无线传感器网络节点定位算法优化研究

段林妍

四川省计算机研究院,四川 成都 610041

0 引言

无线传感器网络是一种分布式传感网络,它是可感知和检查外部世界的传感器。无线传感器网络中的传感器通过无线方式通信,因此网络设置灵活,设备位置可随时更改,还可与互联网进行有线或无线方式的连接,形成一个多跳自组织网络。

无线传感器网络中需要收集各网络节点传感器采集的数据,实现数据汇总和交互,因此,需要对节点的位置进行准确的描述,才能确保采集数据的准确性。

节点定位计算是无线传感器网络中的核心问题。现有的定位算法分为基于距离的定位算法和距离无关的定位算法[1]。基于距离的定位算法适用于定位精度要求较高的应用场景,对传感器节点的硬件要求较高。距离无关的定位算法适用于定位精度要求不高或者硬件功耗低等场景,常用的算法有DV-Hop定位算法、质心定位算法、APIT定位算法等[2]。

目前实际应用较多节点定位算法是DV-Hop算法。DV-Hop定位算法的核心思路是基于距离矢量路由计算,通过节点之间的跳数和平均跳距的乘积来表示节点之间的距离[3]。DV-Hop定位算法是目前应用最广泛的非测距定位算法,该算法在各向同性网络环境中可获得较好的定位效果,但在节点随机分布的网络环境中,由于平均跳距计算误差大、用直线路径代替实际路径等原因,存在较大的定位误差[4]。

本文针对DV-Hop算法中存在的不足,提出了改进优化思路和相应的算法,后续算例验证了改进算法的有效性。

1 现有节点定位算法存在的不足

现有DV-Hop算法的定位思路是采用传统网络中的距离向量路由机制,DV-Hop算法的整个定位过程分为3个部分。

1)计算未知节点到锚节点之间的最小跳数,使用距离矢量交换协议,使网络中所有节点均获得距各锚节点的最小跳数。

2)计算锚节点与未知节点之间的距离。单个锚节点依据来自其他锚节点的位置坐标以及与其自身之间的最小跳数,可计算出其平均每跳距离,即平均跳距。锚节点计算完自身的平均每跳距离后,利用洪泛法将其广播出去,网络中所有节点只接收距离自己最近锚节点的平均跳距,未知节点收到距离自身最近的锚节点的平均跳距后,将其乘以该锚节点到未知节点的最小跳数,即为未知节点到该锚节点的距离。

在DV-Hop算法中,采用锚节点与未知节点之间的最小平均跳距与跳数乘积进行计算,容易产生定位误差,现有的算法主要存在以下不足。

传统的DV-Hop算法中未知节点只将最近的锚节点的平均跳距值作为其平均跳距计算的估计值,而实际情况中,未知节点与多个信标节点间跳数值为1跳时,节点之间的实际距离不一致,传统节点定位算法将节点间估算距离均是按照1跳来处理,从而造成估算误差。由于无线传感器网络部署时因为地理因素会存在空洞现象,造成节点间最短通信距离发生曲折变化。因此,使用DV-Hop算法会带来较大的距离误差,需要根据实际场景进行调整,现有算法适应能力较弱。

2 DV-Hop算法的优化

2.1 优化思路

目前,DV-Hop定位算法的改进思路主要是通过对节点通信距离进行取样,例如锚节点和未知节点的通信距离为R,可将节点通信距离取1/4、1/2、3/4计算跳数,以提高跳数计数的精度。文献[5]中提出了一种基于双通信半径的DV-hop算法,未知节点使用通信半径R,而信标节点使用R和0.5R进行通信,仿真结果表明其定位精度有所提升,但这种改进算法需要依赖实际工程经验才能确定通信半径设置是否合理,能够适配的应用场景较为有限。

本文改进思路是在得到全网平均每跳距离的基础上,通过分析任意锚节点的平均每跳距离误差,修正全网平均每跳距离,使其能接近真实值,从而降低误差,提高精度。

一般来说,锚节点的平均每跳距离误差定义为[6]：

(1)

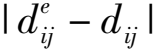
由式(1)可知,可从2个方面减少平均每跳距离误差,一是降低各锚节点计算本节点的平均每跳跳距误差,修正全网的平均每跳跳距值;二是提升节点之间的跳数hij,可将节点通信半径多次取样,以增加节点之间的跳数,逼近1跳的真实距离。

由于未设置准入门槛，“粮食银行”运营主体可能会冲破道德的约束，过分追求经济利益导致企业无法正常运转或破产，出现“跑路”风险，损害农民利益。江西省社科院农村经济研究所副所长尹小健表示，农民将粮食存入“粮食银行”，存在一定风险，粮食行情下行时，经营者的资金链一旦断裂或遭遇不可抗的自然灾害，无力支付利息或提供农资时，“跑路”就不足为奇。

根据现有文献可知,经过大量统计分析,无线传感器分布呈泊松分布[6]。根据参数估计理论,使用均方差比方差更有效[7]。在概率论中,方差是衡量随机变量或对一组数据离散程度的度量[8]。均方误差是各数据偏离真实值差值的平方和的平均数,也就是误差平方和的平均数[9]。

(2)

(3)

式中：dij为锚节点i和j之间的真实距离;ri为锚节点i的平均每跳距离估算值;hij为锚节点i和j之间的跳数;N为总的节点数。

整个无线传感器网络的整体误差为：

(4)

用最小二乘法求解,可得修正过后的平均每跳距离估算值为：

(5)

2.2 改进算法的工作流程

改进算法的工作流程步骤如下。①无线传感器网络初始化。②使用典型的距离矢量交换协议,锚节点在无线传感器网络中广播包含自身位置信息的数据包,使网络中所有节点获得锚节点之间的跳数。③锚节点i利用式(5)计算修正后的平均每跳距离,并广播带有跳数和平均跳距的分组,其他锚节点均需要广播相应的分组。④利用极大似然估计法估算其坐标,程序结束。

3 仿真分析

由于DV-Hop定位算法受网络拓扑结构的影响较大,对于不同的网络结构,定位算法的精度会发生变化。因此,为验证本文提出的优化DV-Hop定位算法的普适性,本文针对不同通信半径和锚节点情况分别多次进行了网络仿真试验。

无线传感器网络区域大小为300 m×300 m,随机布设150个节点,经过多次试验后,取平均值作为仿真的结果。使用MATLAB仿真经典DV-Hop定位算法与本文提出的改进DV-Hop定位算法的性能指标,并进行对比分析。

图1为通信半径为10 m时,本文提出的改进定位算法与传统DV-Hop算法在相对定位误差与锚节点数量之间的关系图。

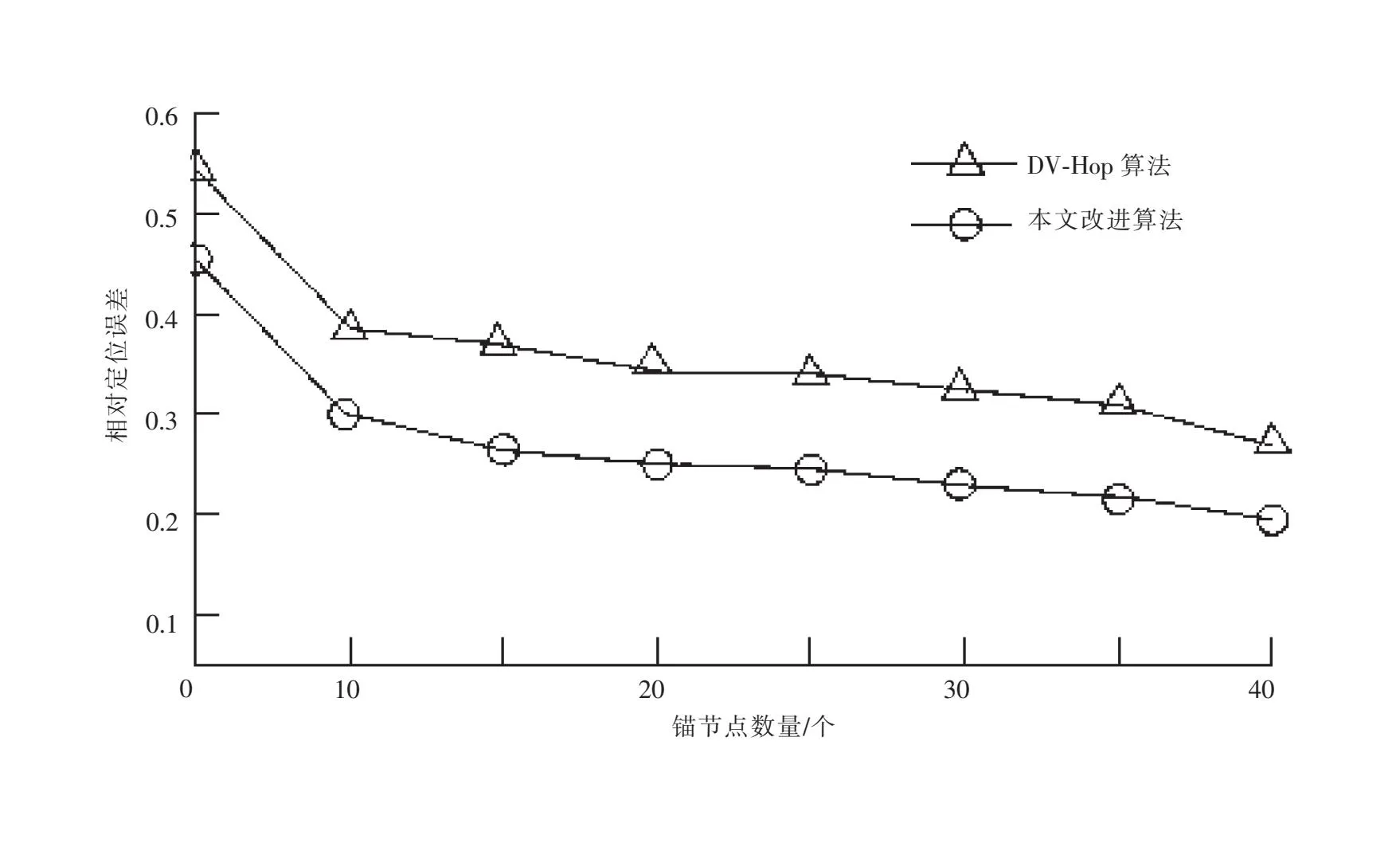
图1 通信半径为10 m时的相对定位误差比较

图2为通信半径增大到50 m时,本文提出的改进定位算法与传统DV-Hop算法在相对定位误差与锚节点数量之间的关系图。

图2 通信半径为50 m时的相对定位误差比较

从图1和图2变化可知：一是在锚节点数量依次递增且通信半径不变的情况下,相对定位误差逐渐变小;二是随着通信半径的增大,相对定位误差逐渐减小。究其原因,通信半径的提升意味着网络连通度的提升,相对误差会减小,说明本文提出算法符合无线传感器网络部署的实际情况。

本文提出的改进算法利用均方差的计算方法,从全网误差的角度进行优化,可有效降低整体误差,并且这种优化方式与无线传感器网络拓扑架构无关。因此,本文提出的改进算法相对于改进跳数计数的优化方法,应用场景更广,更具有普适性。

4 结束语

本文在DV-Hop算法基础上提出了一种改进算法,在得到全网平均每跳距离的基础上,通过分析任意锚节点的平均每跳距离误差,建立均方差优化模型,修正全网平均每跳距离,使其能接近真实值,从而减小误差,提高精度。仿真结果表明改进算法在减小误差和提高精度方面均有所提升。