面向稀疏奖励的机器人操作技能学习
吴培良 张 彦 毛秉毅陈雯柏高国伟
(1.燕山大学信息科学与工程学院,河北 秦皇岛 066004;2.河北省计算机虚拟技术与系统集成重点实验室,河北 秦皇岛 066004;3.北京信息科技大学自动化学院,北京 100192)
1 引言
强化学习与深度学习结合的研究已取得很大的进展,并被成功应用于诸如自动驾驶、游戏对战等领域以解决端到端的决策问题.在机器人操作技能学习领域中,深度强化学习被用于训练机器人打棒球[1]、开门[2]、抓取与放置物体[3]等.对于强化学习来说,智能体通过奖励来优化自己的决策[4],然而在较为复杂的机器人操作技能学习问题中,智能体难以获得正向奖励,稀疏的奖励信号会导致训练缓慢甚至失败[5],这种问题被称为稀疏奖励问题.
针对稀疏奖励问题的研究,根据是否需要引入外部信息可以划分为两类,即需要外部信息引导的方法和无需外部信息引导的方法.其中,需要外部信息引导的方法主要应用于特定的强化学习任务,由于相关知识的引入,该类算法具有实现简单、学习速度快的特点,主要方法包括: 奖励塑性[6]增加附加奖励函数来协助智能体完成目标任务;模仿学习[7]使用现有经验数据进行监督学习,减少了智能体探索环境和学习技能的时间;课程学习[8]将任务分解为不同难度的任务,逐步将学到的策略迁移到难度更高的任务中,降低了智能体在复杂任务中探索的难度.无需外部信息引导的方法一般较为复杂,主要通过挖掘模型或数据的潜在能力来解决稀疏奖励问题,具有较强的普适性,主要方法包括:事后经验回放(hindsight experience replay,HER)[9]用智能体实现的状态来代替训练的期望目标,通过构建虚拟的成功经验来丰富经验池数据,达到加速训练的效果;好奇心驱动[10]引入信息论来推导奖励并建立与好奇心的联系,引导智能体更高效地探索环境;分层强化学习[11]将复杂的强化学习任务分解为不同的子任务来降低任务的复杂度.其中HER算法因无需外部信息引导,鲁棒性强等特点成为解决稀疏奖励问题的主流方法,然而,由于确定性方法的脆弱性,HER通常面临欠稳定性和收敛慢的双重挑战,这会显著影响最终性能.
近年来,信息熵思想逐渐被应用于强化学习领域.Pitis等[12]将最大熵用于解决多目标强化学习任务,Eysenbach和Levine[13]证明了最大熵可以解决鲁棒性强化学习任务,Duan等[14]用最大熵解决值估计错误.在HER算法的基础上,He等[15]结合最大熵概率推理模型,提出软更新事后经验回放(soft HER,SHER)算法以提高算法的稳定性,SHER由温度参数来调节熵在优化目标中的重要程度,但仍存在网络冗余、需人为设置温度参数等问题.
在强化学习任务中,会随机从经验池中抽取批量经验数据来训练算法模型,这样做的目的是为了消除训练数据之间的相关性,然而数据之间的价值并不相同,为了提高数据的利用效率,优先经验回放方法通过计算时序差分误差来确定数据被抽取的优先级,但存在优先级计算复杂、需额外维护的数据结构等问题.在事后经验回放思想中,本文可以将经验数据简单分为采样数据与构建的虚拟数据,并根据两种数据的价值来调节二者被抽取的比例.
元学习又称学会学习,通过数据驱动的方式利用以往的经验来学习一些任务级别的信息[16],可以用于优化超参数,在已有“知识”的基础上快速学习设置超参数直至适合新任务.因此,本文在SHER中引入自适应和元学习经验回放分割思想,提出了基于双经验池的自适应软更新事后经验回放(double experience replay buffer adaptive soft,DAS-HER)算法,将其应用于稀疏奖励下的机器人操作技能学习问题,并在2个环境的8个任务中进行了实验验证.
2 DAS-HER
2.1 多目标强化学习
通用值函数逼近器(universal value function approximators,UVFA)[17]通过引入目标的概念,定义了关于目标g和状态s的广义值函数Vg(s),表达了局部目标的奖励,使机器人能够在一个强化学习环境下实现多个任务的训练.令G为所有目标可能的空间,通常需要不同的奖励函数和最优值函数去完成各种任务方案,UVFA提出将状态s∈S和目标g∈G整合为高维状态(s,g),价值函数V(s)与Q(s,a)则被表示为V(s,g)与Q(s,a,g),其中a表示动作.每一个目标g ∈G都对应一个奖励函数r.在整个回合中目标是固定值,在每一步中,智能体获得当前状态,通过策略π:S×G →A选择动作,获得环境反馈的奖励rt=r(st,at,g)及st+1,如此重复直至回合结束.在策略π下,Q函数不仅仅取决于状态和动作,还取决于目标,可被表示为Qπ(st,at,g)=E[Rt|st,at,g].
2.2 软更新事后经验回放(SHER)
在UVFA框架下,多目标强化学习优化的目标函数可以表示为
其中ϕ为策略π的参数.策略函数的梯度更新依赖于可变性的奖励,但在稀疏奖励环境下,智能体很难通过随机探索达到目标状态,无法收集到足够多可变性信息使训练收敛.为解决这一问题,HER算法通过转换采样获得的经验数据(st,at,st+1,rt,g)中的g,将其更新为未来时刻已达到的目标g′=sk,k≥t,重新计算获得的新奖励=r(st,at,g′),得到虚拟的经验数据(st,at,st+1).HER使得智能体可以获得足够多可变性的奖励信号来学习,做到从失败的经验中学到知识,从而有效解决了稀疏奖励训练难收敛的问题,并显著提高了样本采样效率.
在复杂的多任务强化学习环境中,使用HER算法训练的智能体在不同回合之间经常会陷入波动.为了提高HER算法的稳定性,SHER算法将其与最大熵概率推理模型结合,在原强化学习优化目标的基础上增加了熵项
通过温度参数α来决定熵在优化目标中的重要性,实现了更先进、更稳定的性能.但在使用SHER算法进行训练前,需要人为探索最优的温度参数以达到最优的训练效果.
2.3 自适应软更新事后经验回放
在自适应软更新事后经验回放(adaptive SHER,AS-HER)中,为了适应高维和连续的状态空间,使用函数逼近来求解动作价值函数Qsoft和策略函数π,参数分别表示为θ和ϕ,通过采样数据对动作价值Qsoft网络Qθ(st,at,g)和策略网络πϕ(st,g)进行梯度更新优化,其中策略π被建模为高斯模型,通过策略网络给出均值与方差.
在多目标强化学习中,整个回合的目标g是固定的.根据文献[15],在该前提下,可得贝尔曼方程为
SHER算法通过一个深度网络模型来近似逼近状态价值函数V(s,g).一般的强化学习框架中,状态价值函数V被表示为动作价值函数Q的期望,因此,在最大熵模型下可以使用下式来近似估计V(st,g):
为最小化贝尔曼残差,Qsoft网络的损失函数被定义为Qsoft网络对动作价值函数的估计与式(3)计算的价值之间的均方误差,该误差也被称为单步时序差分误差,如下式所示:
其中:D为重放经验缓冲池,用来存放采样得到的数据五元组(st∥g,at,rt,st+1∥g);θ′为目标Qsoft网络参数,结构与Qsoft网络参数θ一致,并定期通过参数θ进行更新,这样做的目的是基于价值(value based,VB)的方法,贪婪地更新值函数会带来过估计问题,增加目标Qsoft网络可以减少目标值与当前值的相关性.结合式(4)通过梯度下降对参数θ进行优化,即
对于策略网络π,本文希望动作价值函数越大的动作被选择的概率也越大,指数函数则可以很好满足该要求.因此策略π选择动作的概率可以被表示为如下的指数函数:
KL散度可以用来衡量两个概率分布之间的相似性,因此本文希望上式中策略π(at|st,g)与exp(×Qsoft(st,at,g))之间的KL散度足够小,其中KL散度定义为
故将策略网络的损失函数定义为二者的KL散度,即
同时在动作中加入高斯噪声,通过神经网络ϕ输出期望µ与方差σ,令网络的输出为εt,可得到at为
故式(8)中策略网络的目标可改写为
使用πϕ隐式定义fϕ,得到ϕ的梯度优化公式为
在SHER算法中,温度参数α为是固定的,α的值会影响到算法的效率,但确定最合适的α值并非易事,不同的强化学习环境及相同任务的不同时期,最佳α值并不相同.本文希望制定一个最大熵学习目标来动态调整α值,当策略探索到未知的状态时,智能体无法得知最优动作,这时应增大α值使智能体更有探索性,当策略基本确定时,应减小α值以减少探索,为此需要一个具有最大期望奖励且满足最小期望熵约束的随机策略,在文献[18]中,作者提出温度参数的最优解可以由下式求解:
通过函数近似和随机梯度下降的方法近似求解式(12),温度参数α的损失函数可表示为
对于连续状态空间的任务,无法简单的使用式(4)估计状态价值函数V(st,g),为此本文提出了一种精简值函数计算方法.使策略函数π选择每个动作的概率满足正态分布a ∼N(µ,σ2),选择动作的期望值为µ,同理结合式(7)可以得到
式(4)可通过式(15)计算,即
为进一步减少过估计问题带来的影响,本文分别采用参数为θ1,θ2的两个Qsoft网络,对应的目标Qsoft网络参数为,.在对式(5)和式(8)进行实现时,本文使用2个Qsoft网络输出价值较小的一个,并独立对其进行训练和优化.
2.4 基于元学习的经验回放分割
对于自适应软更新经验回放算法,可以将经验池中的数据划分为真实的采样数据和构建的虚拟数据两部分.面对奖励稀疏的强化学习任务,当智能体很难通过真实采样获得正向奖励时,采样得到的数据样本价值低,随着网络性能的提升,采样数据的价值也会得到提高.为了能够在经验回放时灵活地控制真实与虚拟数据之间的比例,本文提出了一种经验回放分割方法,将经验池分割为采样经验池D1与虚拟经验池D2两部分,分别用来存储真实的采样数据和构建的虚拟数据,假设每次采用Nbatch组数据作为训练样本训练网络,则从经验池D1,D2中分别随机抽取(1-δ)×Nbatch和δ×Nbatch组数据,其中参数δ取值在0到1之间.经验回放分割方法不仅打破了经验数据之间的相关性,使得网络在训练中更加稳定,同时还可以保证每次小批量训练时中真实的采样数据与构建的虚拟数据同时存在.
为了不需人为设置参数δ,且能适应任务的不同阶段,可以利用已有知识通过元学习思想学习参数δ使其适应不同任务.在自适应软更新经验回放算法中,收益与策略网络的损失是体现算法表现和策略网络的优化程度的重要指标,也是宝贵的已有知识,为此本文设计了一个深度神经网络对参数δ进行学习,其中网络的输入为收益和策略网络损失,为了最大化奖励,将网络的损失定义为-(δ×r).
完整的DAS-HER算法如算法1所示,智能体执行采样策略选择的动作来收集经验数据,并分别将采样数据和虚拟数据存储到不同的经验池中,通过元学习思想学习比例参数,并根据学得的比例从两个经验池中抽取数据交替对函数逼近器进行随机梯度下降.从失败的经验中学习,从而有效解决了稀疏奖励训练不收敛问题,并显著提高了样本采样效率.
DAS-HER算法在SHER的基础上精简了状态价值函数,并新增了较为简单的超参数网络,由于算法涉及的深度模型较为简单,以Mujoco仿真环境下经典的Fetch,Hand操作技能学习任务为例,3至4层全连接层便可完成任务.因此DAS-HER算法模型的参数数量相较其他算法变化不大,且与任务环境的维度有关.总之,DAS-HER算法的参数量和计算复杂度均与ASHER算法、SHER算法和HER算法持平.

表1 双经验池自适应软更新事后经验回放算法Table 1 Double experience buffer adaptive soft hindsight experience replay algorithm
3 基于AS-HER的机器人操作技能学习
3.1 Fetch和Hand环境的强化学习表示
智能体通过AS-HER 算法进行操作技能学习前,首先要把智能体从环境中分离出来,并将机器人及目标物体的信息符号化为强化环境的状态、目标与动作,常见的机器人操作技能学习Fetch与Hand环境可以符号化表示为
1)Fetch环境: 状态集合S包含抓手与目标物体的坐标位置、抓手的移动速度等信息,维度为25维;目标集合G为目标位置的三维坐标矢量,符号化表示为G={Xobj,Yobj,Zobj};动作集合A为四维矢量来表示机械臂抓手的三维坐标矢量及抓手状态(打开或关闭),可符号化表示为A={Xobj,Yobj,Zobj,grip}.
2)Hand环境: 状态集合S包含机器手24个关节的坐标位置与速度等信息,共61维;目标集合G为目标位置的三维坐标矢量与四维旋转角度;动作集合A为20个非耦合关节的绝对位置.
3.2 基于DAS-HER的机器人操作技能学习
将DAS-HER算法应用到机器人操作技能学习,首先需要构建机器人操作技能学习的强化学习环境,并初始化采样经验池D1、虚拟经验池D2、温度参数α、策略网络ϕ、Qsoft网络θi,i=1,2及超参数网络.策略网络输入层结点个数为状态和目标的维度之和,输出层共两个结点,输出策略高斯分布的期望与方差;两个Qsoft网络结构相同,输入层结点个数为状态、目标和动作的维度之和,输出层仅有一个结点,用来输出动作价值;超参数网络输入层的两个结点用来输入奖励与动作网络的损失,输出层输出数据为参数δ的值.各网络的结构如图1所示.
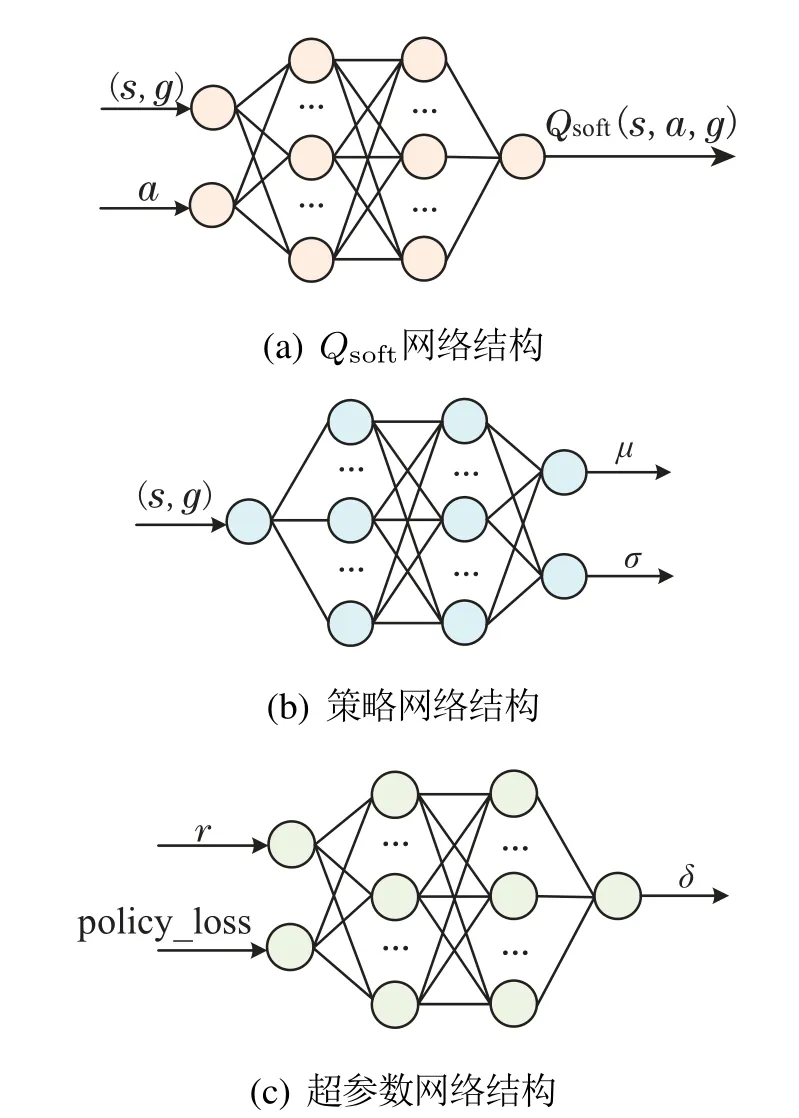
图1 网络结构图Fig.1 Network structure
同时还需制定一套选择动作的策略用来采集训练数据,AS-HER作为一种异步策略算法,学习过程中优化的策略与采集样本时选择动作的行为策略可以是不同的策略.在对数据进行采样时,为了让智能体更加全面地探索环境,在式(12)的基础上,每次选择动作时以概率ρ随机在动作集合A中选择一个动作
上述准备工作完成后,便可对训练所需要的数据进行采样.回合开始时,随机初始化机器人环境及需要完成的目标g,通过传感器获取环境状态st并根据式(16)选择动作at,环境反馈奖励值rt及新的状态st+1等信息,将经验数据(st∥g,at,rt,st+1∥g)保存至回合经验缓存区,奖励函数被定义为二元函数,即
如此重复,直至智能体完成目标或执行步数超过阈值.回合结束后从缓冲区选取经验数据(st∥g,at,rt,st+1∥g),使用本回合后序的n(n≥1)个状态替换目标g并重新计算收益,构造出虚拟数据(st∥g′,at,r′t,st+1∥g′),最后将真实数据保存到经验池D1,构建数据保存到经验池D2中.
网络训练阶段,首先,从经验池D1,D2中随机读取(1-δ)×Nbatch和δ×Nbatch组数据,然后两个Qsoft网络独立计算动作价值函数,选取价值较小的结果通过式(5)和式(10)计算出策略网络与Qsoft网络的损失,并通过式(13)对温度参数进行更新,其次,结合元学习思想,利用策略网络损失和奖励学习超参数δ,超参数网络的损失设置为-(δ×r),最后对Qsoft目标网络进行更新,更新公式如下:
完整的基于DAS-HER的机器人操作技能学习系统如图2所示.

图2 基于DAS-HER的机器人操作技能学习系统Fig.2 Robot manipulation skills learning system based on DAS-HER
4 实验
为评估DAS-HER 算法的性能,与HER,SHER 以及仅用本文自适应思想的AS-HER 算法进行对比实验.为了体现算法的泛化性,选择的任务为Mujoco模拟机器人环境下的Fetch任务与Hand任务,其中奖励策略采用二进制稀疏奖励,成功时奖励为0,其他情况奖励为-1,实验配置如表1所示.

表1 实验配置Table 1 Experimental configuration
4.1 Fetch环境及结果分析
首先,本文选择了Mujoco 环境下的Fetch 机械臂,该机械臂共有7个自由度,并有一个两指抓手.使用Fetch机械臂对以下4个任务进行了实验:
1)FetchReach: 寻找任务,机械臂要将抓手移动到目标位置.
2)FetchPush: 推动任务,机械臂要将桌子上的方块推动到目标位置,在任务过程中机械臂抓手被锁住不进行抓取操作.
3)FetchSlide: 滑动任务,机械臂要用不同的力气去击打桌子上的球体使其滑动,并在摩擦力的作用下最终停在目标位置.
4)FetchPickAndPlace: 抓取与放置任务,机械臂学习靠近桌子上的方块并用抓手将其抓起,然后将方块移动到目标位置,该任务中的目标位置是在空中.
在以上4个操作技能任务中,方块或球体每回合的初始位置与目标位置均是随机生成的,因此可以作为多目标强化学习的实验环境,具体实验环境如图3所示.

图3 Fetch实验环境Fig.3 Fetch experiment environment
在文献[15]中,作者指出在该实验环境下,当温度参数α固定为0.05时SHER算法在任务中效果表现最佳,因此,SHER算法的实验结果均是在α=0.05情况下所得.具体实验结果如图4所示.
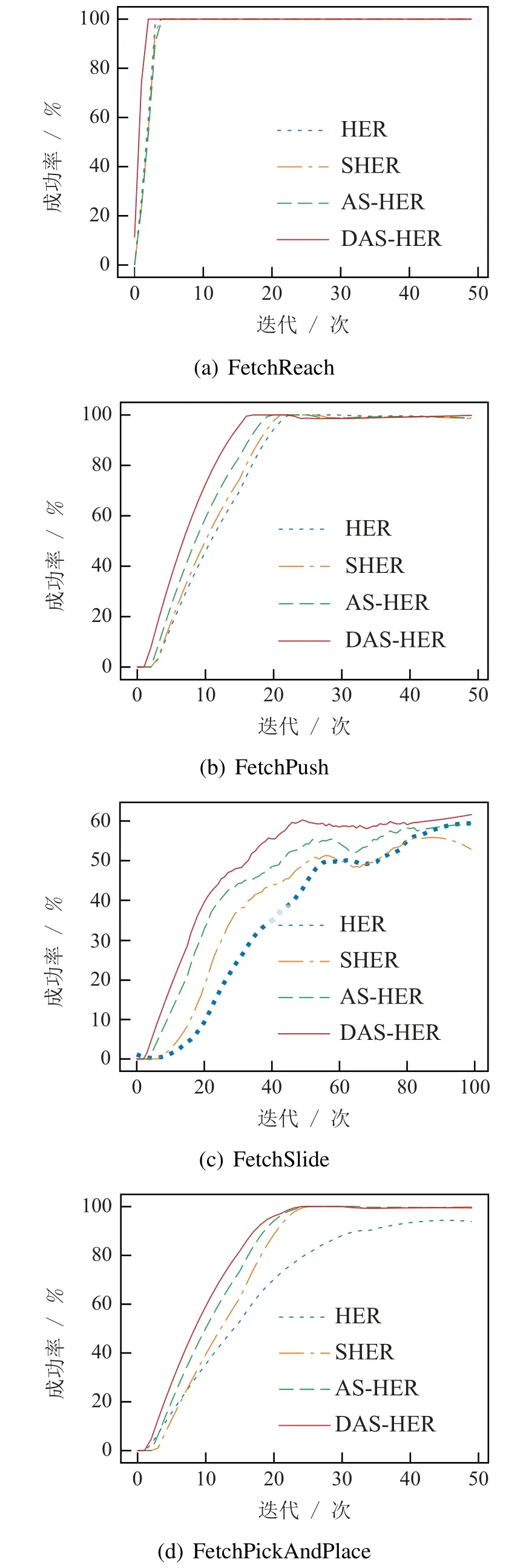
图4 Fetch环境下实验结果Fig.4 Experimental results in Fetch environment
在Fetch环境下的4个机械臂任务中,AS-HER算法的性能均优于SHE和SHER算法.训练前期经过相同的迭代次数,AS-HER相对其他算法能够取得更高的成功率.训练后期由于FetchSlide任务的未知性,3种算法的成功率均无法收敛到100%且会出现震荡,另外3个任务AS-HER可以通过较少的迭代次数使成功率收敛到100%.DAS-HER算法在AS-HER 的基础上引入经验回放分割思想,可以更好地发挥训练数据的价值,因此在4个任务中训练效率均优于AS-HER算法.实验结果证明了自适应温度参数及基于元学习的经验回放分割思想的有效性.
4.2 Hand环境及结果分析
其次选择更加复杂的Hand拟人机器手,该机器手共有24个自由度,其中有20个关节可以自由控制,其余为耦合关节.使用Hand对以下4个任务进行训练:
1)HandReach: 手指捏合任务,训练机器手控制大拇指和另一根手指在手掌上的目标位置接触.
2)HandManipulateBlock: 控制方块任务,训练机器手控制一个方块并将其移动到目标位置和方向.
3)HandManipulateEgg: 控制球体任务,训练机器手控制一个椭球并将其移动到目标位置和方向.
4)HandManipulatePen: 控制笔任务,训练机器手控制一支笔并将其移动到目标位置和方向.
在以上4个任务中,每回合目标物体的位置和方向同样是随机生成的,具体实验环境如图5所示.

图5 Hand实验环境Fig.5 Hand experiment environment
与Fetch环境相同,SHER算法的实验结果均是在α=0.05情况下所得,具体实验结果如图6所示.


图6 Hand环境下实验结果Fig.6 Experimental results in Hand environment
实验结果表明,AS-HER算法及DAS-HER算法在Hand环境下不仅拥有更高的训练效率,在最终成功率的表现上也优于其他算法.为验证算法在复杂任务中的有效性,本文统计了Hand环境下各算法的最终平均成功率,结果表明AS-HER及DAS-HER算法在复杂环境下表现更佳,如表2所示.

表2 Hand环境下平均成功率Table 2 Average success rate in Hand environment
当策略网络无法给出明确的动作时,AS-HER会增大温度参数α,使智能体有更强的探索性以提高探索到更优的动作的可能,当训练逐渐趋于稳定时ASHER算法会减小温度参数α,以削弱智能体的探索性.因此,AS-HER算法无论是在Fetch环境还是Hand环境中,表现都好于SHER 和HER 算法.DAS-HER在ASHER算法的基础上引入了基于元学习的经验回放分割,动态调整训练样本中采样数据与构建数据之间的比例,提高了训练样本的总体价值,使得DAS-HER算法的性能更加优秀.
4.3 精简值函数分析
式(15)提出了一种精简值函数计算方法来求解状态价值函数V(st,g),替代SHER中的V网络以提高算法训练效率.为验证这一改动不会影响算法训练收敛的速度,将AS-HER算法中的α固定为0.05,与SHER算法保持一致,在Fetch环境下进行了对比实验.实验结果证明使用式(15)可以在不影响算法收敛速度的情况下提高算法的效率,结果如图7所示.

图7 α=0.05条件下实验结果Fig.7 Experimental results when α=0.05
4.4 算法复杂度分析
为评估各算法的计算复杂度,本文实验记录了Fetch环境下各算法完成50轮次迭代训练所需要的时间,实验结果如表3所示.

表3 完成训练所需时间Table 3 Time required to complete training
AS-HER算法在SHER算法的基础上引入了自适应温度参数,并精简了状态价值函数的计算方法,实验结果表明AS-HER算法与SHER算法相比有更低的计算复杂度,高于结构简单的HER算法.DAS-HER算法的超参数网络较为简单,因此算法整体的复杂度略高于AS-HER算法,低于SHER算法.
为评估算法总体性能,本文记录了Fetch环境下各算法达到特定成功率所需要的时间,其中因Slide任务难度较大,4种算法的最终成功率只能收敛至60%,本次实验记录了该任务下的30%和60%两种情况,实验结果如表4所示.

表4 达到特定成功率所需时间Table 4 Time required to achieve a specific success rate
实验结果表明,到达相同的成功率,DAS-HER算法所用时间最短,AS-HER算法次之.虽然DAS-HER算法计算复杂度高于HER,AS-HER算法,但出色的性能使其需要的迭代次数更少,因此所用总时间更短.
5 结论
由于机器人操作技能学习问题的稀疏奖励性质,传统深度强化学习算法在求解时效率低下.本文在SHER中,引入自适应和双经验池元学习思想,提出了一种基于双经验池的自适应软更新事后经验回放算法,并将其应用于机器人操作技能学习.
目前关于机器人操作技能学习的研究,其验证实验大部分都是在Mujoco下的Fetch和Hand环境下进行,本文针对这两个不同环境下的8个任务进行了对比实验,表明本文算法较其他算法性能更优,一定程度上验证了算法的泛化性.下一步工作将聚焦在实物实验环境中,进一步验证算法的泛化性.

