动态内全潜结构投影的空间扩展故障检测方法
孔祥玉 陈雅琳 罗家宇 安秋生杨治艳
(1.火箭军工程大学导弹工程学院,陕西 西安 710025;2.航空工业成都凯天电子股份有限公司,四川 成都 610091;3.山西师范大学数学与计算机科学学院,山西 临汾 041000;4.工业和信息化部电子第五研究所,广东 广州 511370)
1 引言
为保证大型装备系统或复杂工业过程安全可靠地运行,对装备或工业过程的状态进行在线实时故障检测至关重要[1].由于系统集成化程度高且缺乏具体的机理知识,难以建立精确的机理模型.而数据驱动的多元统计过程监控方法(multivariate statistical process monitoring,MSPM)具有不需机理模型的优点,因此近年来得到广泛应用.常用MSPM方法有: 独立成分分析(independent component analysis,ICA)、主成分分析、偏最小二乘分析(潜结构投影)、规范变量分析(canonical variable analysis,CVA)等[2–4].这些方法通过将采集的大量高度相关的测量数据投影到低维潜在空间和残差子空间,在各子空间构造统计量实现过程数据的异常监测.上述方法能较早地发现故障隐患,且提高了过程数据的利用率使数据更易使用,因此被广泛应用于复杂系统的故障检测[5].
不同于ICA,主成分分析(principal component analysis,PCA)和CVA方法对全系统的无监督监测,潜结构投影(projection to latent structures,PLS)通过提取过程数据与质量数据的相关特征实现对质量变量的有监督监测.此外,PLS将海量数据投影到低维潜在空间,对质量相关故障进行线性回归,并通过选择较为合适的潜在变量个数,为模型预测方差和偏差提供了一种平衡方法,避免了潜在病态矩阵的直接反演[6],因此受到了广大学者的关注.但是传统的PLS方法在处理传感装置产生的海量数据时,由于当前时刻的样本数据受到历史时刻样本数据的影响,且数据间存在的相关性[7],会导致故障检测结果不可靠的问题.基于此,诸多学者提供了解决方法.Ricker[8]利用有限脉冲响应(finite impulse response,FIR)矩阵提出FIRPLS动态模型;Ku等人[9]提出了动态PCA方法;Li等人[10]提出了一个新的目标函数来获得一个新的动态外部模型,并将其扩展为动态全潜结构投影(total PLS,TPLS)模型,文献[11–14]均致力于消除历史时刻样本对当前时刻样本的影响.同时,Shang等人[15]也给出了另一种解决动态过程监测问题的思路,即在相邻的采样瞬间叠加测量变量来增加输入向量,并将增广矩阵思想应用于马氏距离作为检测指标,该方法提高了动态过程的故障检测效果.
更重要的是,由于现代工业过程通常采样间隔较短,采样数据间不可避免地存在序列相关性,如何有效地挖掘相关特征成为了实施动态过程监测的关键[5].Li等人[10]采用向量自回归(vector autoregressive model,VAR)模型监测动态过程中的异常情况,并用动态潜在变量(dynamic latent variable,DLV)模型对残差空间进行分解,去除变量间的共线性,从而构建了动态TPLS模型;然后,Dong和Qin[16]提出的动态内PLS算法和动态内PCA算法[17],在提取动态潜变量后,利用动态潜变量建立多变量自回归(autoregressive,AR)模型,剔除了动态潜变量间自相关性;Zhou等人[18]将DLV算法与Kalman滤波器相结合,提出了一种自回归的DLV算法并将其应用于动态过程监测;随后,Dong和Qin[6]通过对多维时间序列数据进行预测建模的动态潜变量方法进行综述,进一步揭示了潜变量分析的本质和目标.
针对基于动态内偏最小二乘(dynamic inner partial least aquares,DiPLS)算法由于未按降序提取主要成分,导致残差空间仍存在较大变异,动态和静态信息难以有效分离,影响故障检测性能的问题,本文提出了一种动态内模型的改进算法,即基于动态内全潜结构投影(dynamic inner total PLS,DiTPLS).本文首先将DiPLS算法应用到故障检测中,提取了输入输出间的动态信息和潜在得分间的自相关关系;同时分离了质量Y相关的信息和质量无关的信息;接着利用结构化动态PCA算法改进的DLV方法将含有较大差异的质量无关信息在DiPLS的残差空间进一步分解,将残差中的动静态信息和大小的差异信息进行有效分离,并构造合适的统计指标,建立了完整的过程监测策略.
2 DiPLS算法基础理论
标准PLS算法从输入数据中提取潜在变量来解释输出数据,并在输入和输出数据之间建立线性代数关系.对m个过程变量进行n次不同采样测量,形成输入矩阵X.对p个质量变量进行n次不同采样,形成输出矩阵Y.假设X的潜在变量为t=Xw,Y的潜在变量为u=Y c,w和c为权重向量,PLS的目标函数是寻求潜变量之间的协方差最大,即
显然,这个目标只描述了输入数据中与输出数据最相关的静态变化.但是,它不能提取输入输出数据之间的动态变化或关系.基于此,Dong和Qin[16]提出了一种用于动态数据建模的动态内PLS建模方法,使外部模型的潜在因素更易于解释.当前k时刻的输出潜变量uk与历史时刻输入潜变量tk之间动态关系的模型构造如下:
其中:rk为当前时刻残差;βi为输入得分t的权重系数,i=0,1,···,s,s为系统模型阶数.内部预测模型为
其中:β=[β0β1··· βs]T,β ⊗w为克罗内克积.由此,DiPLS的目标函数是寻找uk与之间的相关程度(或协方差)最大化,故目标函数可以被表述为
其中N=n-s.
给定训练集输入输出样本{Xxun,Yxun},采用归一化的预处理方法消除数据间差异的影响,得到数据{X,Y},xi和yi表示第i个采样点的数据,则X和Y表示如下:
利用增广数据矩阵的原理对输入输出矩阵进行数据扩充,可以得到
故DiPLS的目标函数可以被重新表述为
该目标通过搜索权重向量w和系数矩阵β来表示过程变量空间主要的质量相关的动态变化.这种动态扩展不增加w的维数,并从原始空间中提取动态相关的显式潜在变量.采用拉格朗日乘子法优化该目标函数,对β和w求偏导后可以得到q,w和β的具体计算公式.用提取的动态潜在分数对输入矩阵X进行压缩,循环迭代直到提取出所有的潜在信息.在附录1中总结了DiPLS算法的详细步骤.
由于输入X的得分矩阵T无法直接从Xxun计算得到,故引入权重矩阵R:R=[r1r2··· rA],rj=wj·()-1,j=1,2,···,A,A为主元个数.
由此,输入X的空间被DiPLS算法分解为
式中:P=[p1p2··· pA]为自变量X的负载矩阵;,Q=[q1q2··· qA]分别为Ys的得分矩阵和负载矩阵;Ed,Yd分别是数据矩阵X,Ys经过DiPLS处理后的动态残差.
3 动态内全潜结构投影的故障检测方法
DiPLS对于动态系统具有很好的预测能力,但是Dong和Qin[16]并没有将DiPLS算法应用到故障检测.因此本节首先基于DiPLS提出采用向量自回归的动态故障检测方法;此外,针对DiPLS的残差空间包含较大的变异,且动态静态信息尚未完全分离,提出了扩展DiTPLS算法,构造更加合理的统计量.
3.1 基于DiPLS算法的故障检测方法
文献[17]指出由于采样间隔较短,采集到的数据可能呈现出自相关或互相关关系,因此有必要将潜在得分变量进行动态扩展,以便使用过去的数据预测当前值.这样操作有以下优点: 1)当前时刻的得分分量可以作为已知信息从过去的数据中预测出来,因此不确定性只存在于预测误差上;2)可以构建更加合理的统计量和控制限,使得故障检测结果更加可靠.
为了方便统计监测[17],将得分矩阵ti=RTxi动态扩展为Ti=[ti ti+1···ti+N].建立Ts与T0,T1,···,Ts-1之间的动态关系为
通过对历史数据的预测,得分向量的预测误差为
此时输入X和输出Ys被压缩为
由于Ti在时域内是自相关的,采用T2统计量直接进行监测会导致高误报率.文献[11]表明,v几乎与之前的时刻无关且具有较大的变异性,因此适合用独立无关的v来反应Ts的变化.
3.2 扩展DiTPLS算法的模型
虽然DiPLS是一个动态模型,但它对X空间进行了静态分解,因此残差Ed中仍存在较大差异,如动态、静态的互相关关系,会导致仅使用Q统计量监测不合理.同时文献[12]也指出现有的动态建模方法没有区分动态关系和静态关系,且许多滞后变量在扩展向量中并不能保持原变量空间的结构.为了在动态模型中保持残差的空间结构,本文基于结构化动态主层次分析(dynamic principal component analysis,DPCA)算法提出一种改进的动态潜变量模型用于动态残差的分解,并描述了残差变量间的动、静态之间的相互关系,方便建立合适的统计指标进行监测.
对βd和wd求偏导,得到
根据克罗内克积的性质,可以得到
为了方便后续计算,定义下式
结合上述已知信息,式(19)–(20)可化简为
使式(25)中各项右乘和,结合式(17)中的约束条件和一阶偏导的性质,为了使目标函数最大化,可以得到以下结果:结构化DPCA算法空间分解与DiPLS算法十分相似,即
式中Eg,Pd分别为Ed的动态残差和动态负载矩阵.
同时潜在变量数据中包含的较多的动态特性,也需通过建立动态模型来体现其内部的自相关特性.于是用时间序列模型(或向量自回归模型,VAR)将当前时刻k的得分向量tdk描述如下:
在提取质量无关的动态因素后,Eg的自协方差很小,这为进一步提取静态相关的信息提供了条件.因此,有必要通过静态PCA算法进一步分解Eg,提取质量无关的静态信息,即Eg=Tg+Es,其中:Tg为静态得分矩阵,Pg为静态负载矩阵,Es为静态残差矩阵.在表1中总结了基于结构化动态PCA的改进DLV方法的回归建模流程的详细步骤.

表1 改进DLV模型的算法步骤Table 1 Algorithm steps of improving DLV model
本文所提扩展DiTPLS算法首先采用DiPLS算法提取质量相关的动态信息,随后采用改进的DLV模型进行残差分解.基于DiPLS的扩展算法提取了低维潜在空间和动态残差空间中的大部分动态变化和较大的静态变化,显式地表达了动态、静态关系;也明确地提取了自相关和互相关信息,并在动态模型中保持可变的空间结构,进而使动态模型具有清晰的数学描述.数据空间最终被分解为
所提算法DiTPLS在输入空间上进行了倾斜分解,不同的子空间中描述了不同变量之间的动态关系和各变量之间的自相关关系,如式(32)所示.
因此不同空间有不同的含义:SY表示质量相关的动态子空间;SD表示质量无关的动态子空间;SG表示质量无关的静态子空间;SE表示残差空间.
3.3 基于DiTPLS算法的过程监测策略
本文所提算法分别对质量相关部分采用DiPLS算法进行建模与监测,质量无关部分采用改进的DLV算法进行建模与监测.当给定一组新的测试样本{xce,yce},经预处理后得到{xnew,ynew},分别构造如下过程监测指标:
基于DiTPLS模型构建的统计指标总结如表2所示.对于T2统计量,控制限由主元个数A、样本数n以及置信度α确定,且服从F分布;Λ为得分向量t的协方差矩阵,由训练样本进行估计;对于Q统计量,g=S/(2µ),h=(2µ2)/S,µ为样本均值,S为样本方差,且服从χ2分布.这些检测指标对统计过程监控具有显著的意义.表示动态主潜变量中的统计独立信息,包含数据中的主要动态变化;表示残差的动态主潜变量中的统计独立信息,包含残差中与质量无关的动态变化;反映静态主变化,其中包含数据中的静态变化;Qs反应了正常未激发的或未建模子空间的变化.

表2 DiTPLS模型的统计指标Table 2 Statistical Indicators of DiTPLS model
综上所述,将所提DiTPLS算法的完整建模过程和过程监测步骤总结如下:
1)将训练样本数据经预处理、数据扩充后进行DiPLS动态建模,提取动态潜在变量,捕捉质量相关的动态变化,计算控制限Jth,T2y;
4 实验验证
4.1 数值仿真实验
为说明DiTPLS模型的有效性,用数值仿真案例验证.输入输出均由动态模型生成,如式(33)所示,其中矩阵A1,A1,P,C1,C2,B1,B2的参数参考文献[10]中的数值仿真案例,其中ek ∼N(0,0.12I5),vk ∼N(0,0.12I2),tk ∼N(0,12I3),(0,12I3).此次数值仿真中生成1000个数据点: 其中训练集的数据均为未注入故障的正常样本;而测试集的前200个数据点为正常样本,后800个数据点为故障样本,方便形成对比实验用于对比检测结果.本文所提DiTPLS模型通过交叉验证确定的最优参数为A=3,Ad=3,系统模型阶数为s=3.并选取动态总PLS(DTPLS)[10].DTPLS有着与本文所提算法DiTPLS相似的空间划分方式: 质量相关的动态子空间SY、质量无关的动态子空间SD、质量无关的静态子空间SS以及反应残差变化的子空间SE,通过交叉验证选取的主元个数为ADT=3,模型阶数sDT=3.
对于故障检测效果的验证,可以通过比较质量相关故障样本中实际检测到的故障个数与故障样本总数的比值即故障检测率(fault detection rate,FDR)来表现;由于质量无关故障对输出无影响,因此质量无关故障样本在实际检测时不应该检测到故障发生,若检测到故障发生则表明此时发生了误报警情况,即用故障误报率(false alarm rate,FAR)来表现.若前者越接近1,则表明所提算法对质量相关故障检测效果越好;若后者越接近0,则表明所提算法对质量无关故障的检测效果越好.
1)当tk=tk-1+[0,4,4]T,k≥200,质量相关子空间受到了明显影响,质量无关子空间未发生故障,此时表明发生了质量相关故障,如图1–2所示.经计算DiTPLS和DTPLS在质量相关动态子空间的故障检测率达到了99%以上,能较好的提取出质量相关的动态信息.在质量无关的动态子空间和质量无关的静态子空间,DiTPLS误报警情况出现的次数明显多于DTPLS.造成这样的原因可能是在采用改进DLV模型对残差进行动静态信息分离时,为保持残差的空间结构做出的牺牲.

图1 DTPLS对质量相关故障的检测结果Fig.1 DTPLS detection results for quality-related faults

图2 DiTPLS对质量相关故障的检测结果Fig.2 DiTPLS detection results for quality-related faults
从图中可以发现前200采样时刻都有少量统计量超过控制限的现象,但又会立马会恢复到控制限以下,使整体样本都保持着相同的趋势.造成这种现象的原因是T2统计量的控制限由主元个数A、样本数n以及置信度α决定,而一般选取的置信度α=0.99,故存在的少量噪声或微小变化会使得少量数据超过控制限.
2)当xk=xk-1+[3.70000]T,k≥200,质量无关空间受到明显影响,质量相关空间无变化.图3–4展示了质量无关故障发生时DTPLS和DiTPLS算法各子空间的监测效果,并给出了部分数据的放大图.经计算对于质量无关的故障,在质量相关的动态子空间DiTPLS发生故障误报警率为的故障为7.88%,而DTPLS的误报率为11.78%.在质量无关的静态子空间中,DiTPLS能检测到所有的质量无关故障样本,而DTPLS仅能检测到30.2%的故障.在质量无关的静态子空间和残差子空间,两种算法都有较好的检测效果,故障检测率均在98%以上.

图3 DTPLS对质量无关故障的检测结果Fig.3 DTPLS detection results for quality-independent faults
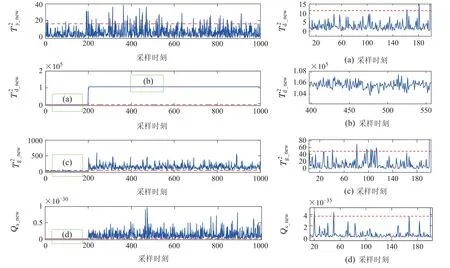
图4 DiTPLS对质量无关故障的检测结果Fig.4 DiTPLS detection results for quality-independent faults
通过数值仿真的实验表明: DiTPLS和DTPLS算法都能较好的提取质量相关的动态信息,对质量相关故障保持较好的故障检测效果;但对于质量无关的故障,本文所提DiTPLS算法具有明显的优势.
4.2 TE过程仿真实验
田纳西–伊斯曼(Tennessee-Eastman,TE)过程是一个典型的包含快速和缓慢动态混合特性的复杂过程,被广泛应用于动态过程的故障检测与故障诊断实验验证,文献[19–21]也表明该过程确实具有动态特性.因此,本节采用田纳西–伊斯曼实验仿真平台得到的公开数据集进行实验验证.
TE仿真平台在仿真时,通过对输入的进料量、浓度等的控制得到41个过程变量和11个操纵变量,共52个的观测变量,也可以模拟21种故障.获取的数据样本大致分为正常数据样本d00.dat和不同故障类型的样本d01.dat–d21.dat.正常数据样本是在25 h运行仿真下获得,观测数据总数为500.而对于故障样本,是在48 h的仿真下获得,获取960个样本,其中包含160个正常样本和800个故障样本.文献[22–23]指出区分质量无关故障与质量相关故障的标准是: 对于选定的质量输出过程变量或输出残差的统计量,如果能被包含故障的输入变量所影响(即超过控制限),且受影响的样本数占故障样本总数超过0.1,那么该输入变量为质量相关故障,反之则为质量无关故障.关于TE过程的故障描述,故障分类可参看文献[24–26].
本文选取的输入变量为过程变量(1–22)与控制变量(1–11),质量输出变量为过程变量(35).通过交叉验证选取主元个数:Ad=6,Ad=16,模型阶数sDiT=3.DTPLS通过交叉验证选取的主元个数为ADT=4,模型阶数sDT=3;DMPLS[27]将输入空间分解为质量相关动态空间和残差空间,选取的主元个数为ADM=1,模型阶数sDM=3.
对于质量相关部分,将3种算法的故障检测率结果总结如表3所示.由表中数据可以发现: 3种算法在提取质量相关的动态信息时,DMPLS对故障5和故障10有非常好的监测效果,检测率有较大幅度的提高,分别达到了99.38%和67.67%;DTPLS算法能监测到故障14的所有故障;而本文所提DiTPLS算法能更好的监测到故障1–2,7–8,13的发生,特别是对于故障7–8的故障检测率均提高了将近20%;在提取质量无关的动态信息时,DTPLS和DiTPLS对各个故障的误报警情况都较为严重,如故障1–2,6–8,12–14的误报率均在90%以上,部分故障的误报率率高达99%,几乎不能监测到质量无关的动态信息;在提取质量无关的静态信息时,DiTPLS算法对故障7的误报警情况有明显的降低,而DTPLS算法对故障5,10存在更少的误报警情况,特别是对于故障10的监测,故障误报率降低了70%.图5展示了故障7的质量相关动态子空间监测图和DMPLS算法部分测试数据的局部放大图,从图中可以看到: DMPLS算法仅在故障发生时刻附近能较好的监测到故障的发生;与DiTPLS算法相比,DTPLS算法能监测到部分故障,故障漏报的情况较为严重;DiTPLS算法能监测到大部分的故障,但也存在少量故障漏报的现象.
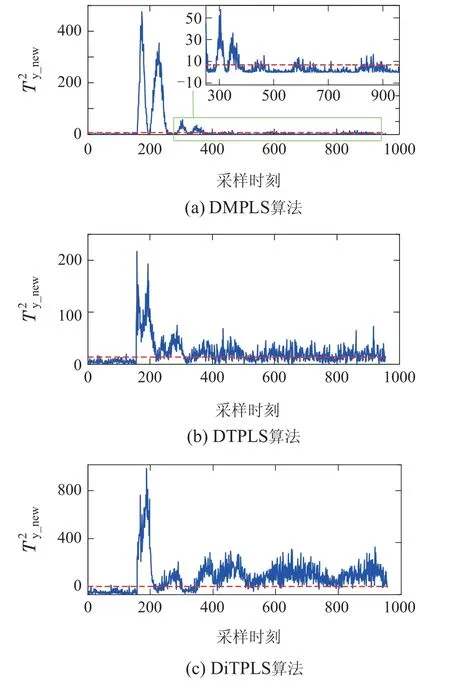
图5 故障7的质量相关动态子空间监测图Fig.5 Quality-dependent dynamic subspace monitoring diagram of fault 7

表3 质量相关故障检测率(%)Table 3 Quality-related fault detection rate(%)
对于质量无关的部分,将3种算法的故障检测率结果总结如表4所示.由表中数据可以发现: 对于质量相关的动态子空间,DMPLS的故障误报率较大,对故障4,11的误报率达到了将近30%;DTPLS算法对故障4误报率较低;而DiTPLS算法对故障3,9,15的误报率较低,仅有不到3%;但是3种算法对故障11都有较高的误报率;对于质量无关的动态子空间,DTPLS和DiTPLS算法的故障检测情况基本相似,对故障4,11检测率情况较好,对微小故障3,9,15检测率情况较低,但两者中DiTPLS算法具有更好的故障检测效果;对于质量无关的静态子空间,DTPLS和DiTPLS算法对故障3,9,15的检测结果基本类似,检测率不到5%;对于故障4,11,DiTPLS的检测率较低,漏报警的情况较为严重.总的来说,在质量相关的动态子空间,DiTPLS算法具有更少的误报警;在质量无关的动态子空间,DiTPLS算法具有更好的故障检测效果;但在质量无关的静态子空间里,DTPLS算法有更好的故障检测效果.
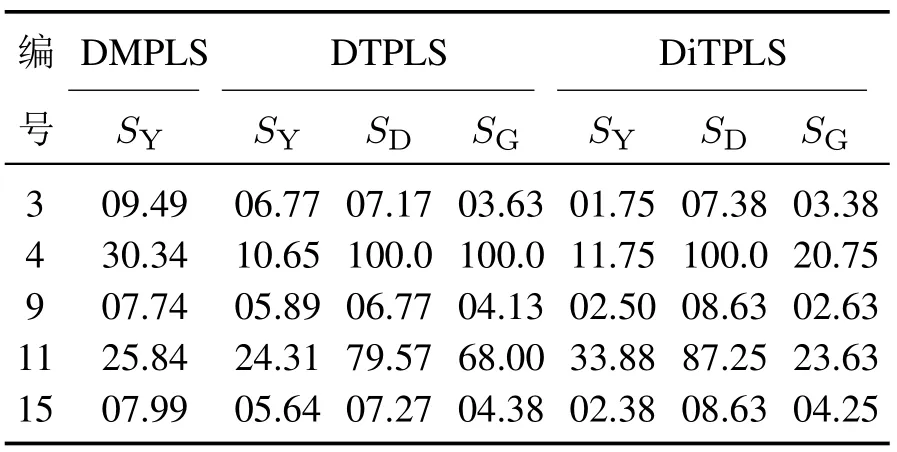
表4 质量无关故障误报率(%)Table 4 False alarm rate of quality-independent faults(%)
在图6中展示了故障15在质量相关动态子空间的监测结果图,横坐标为采样时刻,纵坐标为计算的统计量值,从图中可以明显看出DiTPLS算法有更少的故障误报情况.在图7中展示了故障15在质量无关子空间的监测结果图,2种算法的故障检测情况相差不大,比较明显的是2种算法对动态部分的检测效果都比静态部分的检测效果要好,说明2种算法都能更好地提取质量无关的动态信息.
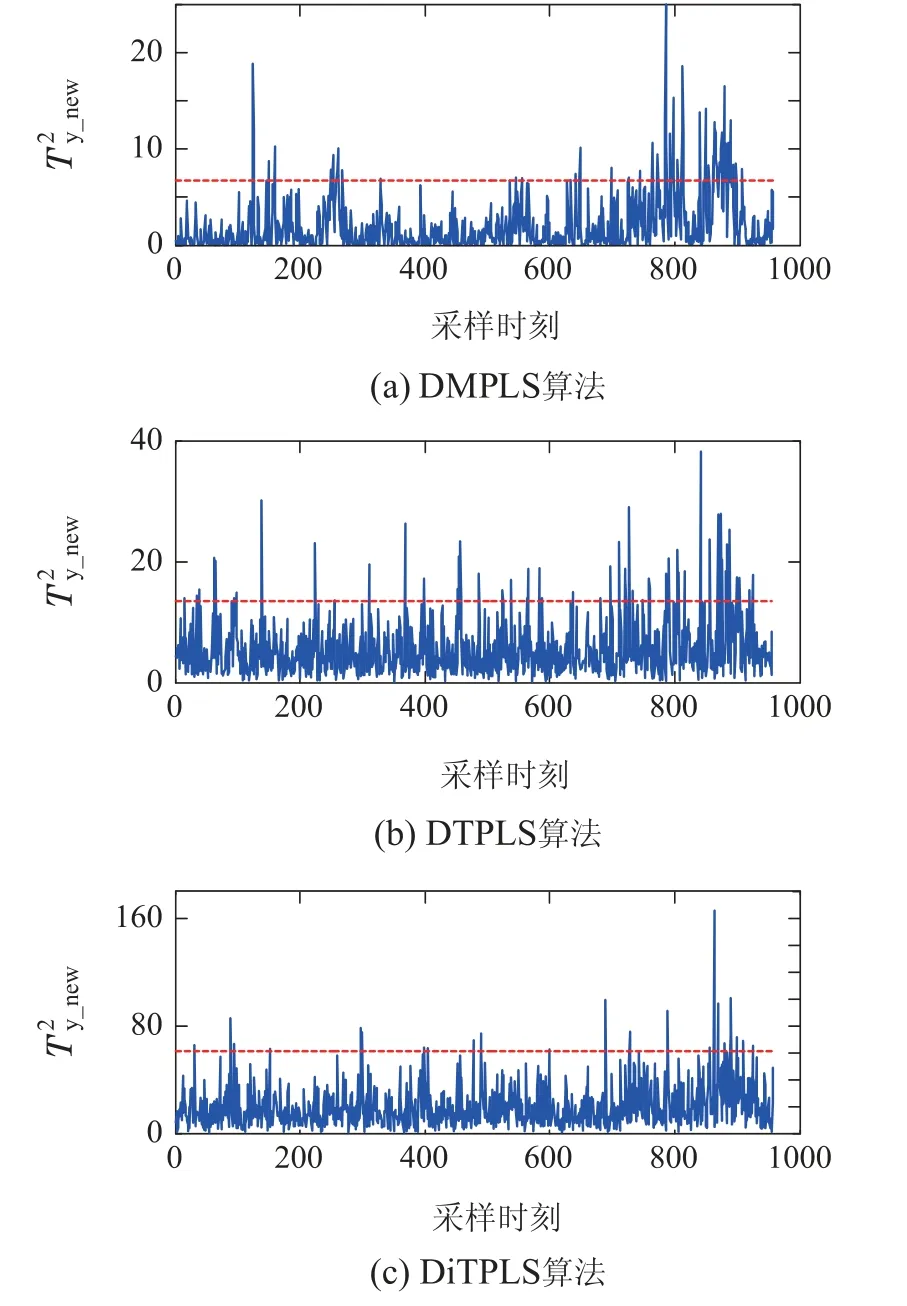
图6 故障15的质量相关动态空间监测图Fig.6 Quality-dependent dynamic space monitoring diagram of fault 15

图7 故障15的质量无关空间监测图Fig.7 Quality-independent space monitoring diagram of fault 15
实验结果表明: 1)该模型是DiPLS模型的动态扩展,可有效地检测与质量相关的异常情况;2)DiTPLS模型没有改变对输出Y的预测能力,但它分解了输入X的残差空间;3)该算法捕获了质量数据块和测量数据块之间的动态关系以及残差中的相关性信息,并将测量数据块分解成4个子空间分别构造各自的统计量,建立了一套完整的故障监测策略,提高了故障检测性能.
综上所述,DiTPLS算法能更好的监测到质量相关故障的发生,能较好的提取动态信息;对质量无关故障有更少的误报警.但是对于质量无关的静态信息,DTPLS 算法对于质量相关的故障有更少的误报警情况,对于质量无关的故障有更好的检测效果.
5 结论
本文提出了一种基于DiPLS的扩展方法,该算法采用DiPLS算法提取主要的动态变化,并基于结构化动态PCA算法构建的潜在变量模型提取残差空间的动态特征.所提取的动态信息和残差中的协方差信息使模型有清晰的数学描述,提高了质量相关空间的过程监测性能,也提高了一些微小故障的检测灵敏度.与DTPLS和DMPLS方法相比,DiTPLS提高了质量相关故障的检测效果,又能很好地提取质量无关空间的动态信息.并通过数值仿真和TE过程的数据,验证了所提算法的有效性.
本文所提算法在质量无关静态子空间对质量相关故障的误报率漏报率轻微上升,对质量无关故障的检测率有较大下降,因此如何更好的提取质量无关的静态信息和基于该方法的故障诊断方法是在以后的研究中急需要解决的问题.
附录1 DiPLS算法的详细步骤
建立外部模型:

