基于改进MPC的重载铁路移动闭塞系统下列车编队控制方法研究
林正南,俞花珍,邰国璇,郭 玮,石 竹,余立伟,黄友能,4
(1.北京交通大学 电子信息工程学院,北京 100044;2.国能朔黄铁路发展有限责任公司,河北 肃宁 062350;3.交控科技股份有限公司,北京 100070;4.北京交通大学 轨道交通运行控制系统国家工程研究中心,北京 100044)
重载列车在大宗货物的运输方面具有运能大、效率高、成本低等方面的显著优势[1]。为提升重载线路运输能力,既有线可以采取的措施有提高列车的速度、密度及重量。列车速度、重量的提升受到线路环境、设备条件等因素的限制不易实现[2],但通过提高列车运行密度是满足运能提升的主要手段之一[3]。当前,编队控制技术正在北京地铁11号线工程示范应用[4],它能够大幅缩短追踪间隔,提高运输能力。相比城市轨道交通列车,重载列车载重大、编组长、操控难度大,且对平稳性要求高,目前国内外针对重载列车的编队运行控制方法研究还较少。
编队运行技术是一种基于现有移动闭塞系统[5]实现列车协同控制的列车控制技术。编队运行技术是欧洲“Shift2Rail”计划的关键组成部分,编队运行技术能够提升既有线资源配置、提高线路容量和运营灵活性[6]。Aoun等[7]分析了编队运行的可行性和适用性,研究表明编队运行对市域和货运市场客户的吸引力很大。
现有研究建立了几种以高速列车和城轨列车为对象的编队控制方法。Pan等[8]采用非线性追踪策略,提出一种动态跟踪控制方法实现了高速列车编队控制。Liu等[9]采取多智能体的控制方法去控制高速铁路列车达到一致的状态。Chen等[10]提出一种基于集中式模型预测控制(model predictive control,MPC)的列车协调碰撞抑制方法,该方法研究了高速列车编队的紧急停车问题。另一些研究以城市轨道交通为对象,提出编队协同控制方法。Félez等[11]建立了采用分布式的MPC框架,对参与编队的每列列车进行控制,该方法提前通过动态规划方法为列车编队中各列车确定最优运行曲线。Wu等[12]结合惰行策略使用MPC方法对城轨列车编队进行了控制,并改善了控制器的输出抖动。She等[13]对城轨列车编队协同控制问题提出MPC控制器的优化目标和约束条件,并用李亚普诺夫稳定性理论验证了稳定性。
但这些研究将被控对象视作单一质点,并且对控制方法中的非线性问题和平稳性问题研究较少。重载列车的编组方式和行车特点与中短编组客运列车存在较大差异,因此现有研究成果不能直接应用于重载列车。在重载列车中使用单质点模型会导致整个列车的受力分布不合理。因此本研究建立多质点模型以描述重载列车编队,更贴合实际运行情况,并将模型参考自适应控制思想引入MPC方法中,增加自适应反馈环节。通过引入0-1指标变量的方式,求解重载列车非线性和平稳性特点的优化问题。
本文主要提出一种重载列车编队运行控制方法,首先基于多质点模型和戴维斯方程,建立考虑运行阻力的列车动力学模型。引入0-1指标变量,将非线性约束转化为线性约束问题,并求解了混合整数的二次优化问题,通过增加自适应反馈环节,设计MPC控制器。最后,采用朔黄铁路重载移动闭塞系统[14]下的实际线路数据和列车数据,在该系统的仿真平台上进行了仿真,通过仿真结果数据说明所提方法的有效性。
1 基于多质点的列车动力学建模
在实际铁路线路中,重载列车由机车和车辆组成,机车负责为列车运行提供动力,车辆负责承载货物。因此,可将每一台机车或车辆看成一个质点,建立列车纵向动力学模型,见图1。

图1 列车纵向动力学模型
图1中,将单元列车中的机车或每一节车辆分别视为一个质点,对每一个质点进行受力分析,有
miai=Ft/b+Fi-Fi+1-Fri-Fgi-Fpi
(1)
式中:n为质点的数量;i为质点的编号,i=1,…,n;mi为质点i的质量;ai为质点i的加速度;Fri,Fgi,Fpi分别为质点i所受的曲率附加阻力、坡度附加阻力和基本阻力;Ft/b为牵引和制动力,仅作用于机车。
曲率附加阻力、坡度附加阻力、基本阻力的表达式为

(2)
式中:Ri为曲率半径;Ii为质点i处的坡度千分数;c0i、c1i、c2i分别为戴维斯方程的经验系数,由TB/T1407.1—2018[15]《列车牵引计算第一部分:机车牵引式列车》通过实验得到的经验数值;vi为质点i的速度。
Ri和Ii由线路位置决定,没有明确的解析式,只能以分段函数的形式表达,以wi为附加阻力的和,则wi=Fri+Fgi。
设Fi为列车内部的受力,用si表示质点i的位移,当si+1-si>0时,车钩被拉长,车钩力作为牵引力产生,有助于保持列车车厢的协同运行。否则,车钩将被压缩,列车内的力将作为制动力产生。此处,文献[16]中车钩力Fi可以表示为两辆相邻车厢的相对位移和相对速度的线性函数
Fi=d(vi+1-vi)+k(si+1-si)
(3)
式中:k为车钩刚度系数;d为车钩阻尼系数。
牵引力和制动力受限于机车的最大功率,HXD1型机车的最大电牵引特性曲线可表示为

(4)
制动特性曲线可表示为

(5)
式中:v为机车运行速度。

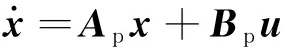
(6)

Ac=diag[c11c12…c1n]
上述连续时域状态空间方程可通过欧拉法离散,采样周期为Ts,离散形式的状态方程为
x(k+1)=Ax(k)+Bu(k)
(7)
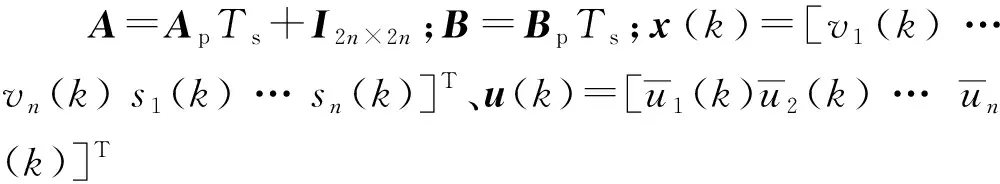
2 基于改进MPC的控制方法设计
重载列车控制器结构见图2,线路限速vline和当前列车的期望速度vdes作为控制器的输入,上位控制器输出控制量udes为当前列车期望牵引制动力,下位控制器根据udes输出牵引制动电流,由牵引制动执行机构输出实际牵引制动力Ft/b。本文提出的控制方法应用于编队中各列车的上位控制器,并将下位控制器和牵引制动执行机构视作动力系统。

图2 列车控制器结构
2.1 列车编队描述
考虑一个多列重载列车组成的重载列车编队,编队头部的第一列重载列车,称为首车。在编队运行中,列车i=i-1是列车i的前车,列车i是列车i-1的后车。本文假设在编队运行过程中,前车和后车之间存在通信链路,在每一时刻,前车都能将本车的速度v、位置s等信息传递给后车,见图3。

图3 重载列车编队
首车的任务是尽可能带领列车编队跟踪既有的目标速度曲线,而后车的任务是保持和前车的间隔,并使相对速度最小。图3中下标f表示为后车,下标l表示前车。在编队运行过程中,控制目标可描述为

(8)
对于编队中的任何相邻的两列车,在任何时刻间隔都必须大于最小安全距离Dsafe。
2.2 自适应反馈的MPC方法设计
模型预测控制(MPC)是一种先进的过程控制方法,能够周期性基于当时刻测量信息,在线求解有限时间开环优化问题,并将结果的控制序列作用于被控对象[18]。MPC能基于模型对系统未来动态行为进行预测,通过把约束加到未来的输入、输出或状态变量上,可以将约束显式表示在一个在线求解的二次规划或非线性规划问题中,因此能够显式处理约束问题[19]。
由于重载列车具有编组长、载重大的特点,模型呈现多质点的特征,为更好改善重载列车在跟踪运行过程中的平稳性和追踪控制性能,本文充分利用MPC能够预测多个时刻列车的位置和运行状态,显式处理列车运行过程中的各项约束的优点,对控制方法进行设计。
MPC方法通过求解在线优化问题来控制列车的牵引力/制动力,该优化问题使代价函数在预测间隔Np内最小化,并满足约束条件。每个时刻控制器根据当前的可用信息预测列车的未来状态。预测完成后,优化问题得到解决,从而产生一系列控制信号。然后将此序列中的第一组控制量应用于列车,其余将被丢弃。当下一个时刻到达时,重复包括状态预测、优化问题求解和应用第一个控制量的过程。通过在有限预测时域求解优化问题,得到当前时刻的最优解。
根据状态方程(7),可以写出递推公式,整理得到

(9)

X=[x(k+1|k)x(k+2|k) …x(k+Np|k)]T
U=[u(k|k)u(k+1|k) …u(k+Np-1|k)]T
式中:x(k+1|k)为k时刻对k+1时刻状态的预测;u(k+1|k)为k时刻对k+1时刻的最优控制量的预测。
由式(9)可以建立优化问题,将优化问题设计为二次规划形式,与其他已知优化方法相比,二次规划对解决带等式和不等式约束的优化问题求解速度更快[20],其一般形式为minJ=(R-X)Q(R-X)T+UHUT,其中,R为列车的目标曲线,Q、H为优化权重系数。优化问题的具体数学描述在2.3节说明,求解可得当前最优控制序列。
MPC方法只能得到当前时刻预测时域内的最优解,因此预测时域大小影响系统整体性能表现,预测时域越大性能越好。但出于对控制方法的实时性的考虑,预测时域不能取值太大。因此对MPC方法进行改进,通过自适应反馈环节对目标曲线进行修正生成参考曲线。编队中首车和后车的目标曲线不同,下文分别说明了首车、后车的参考曲线生成方法以及最终的控制方法流程框架。
2.2.1 首车的参考曲线设计
编队中的首车是编队中的第一辆车,它的目标曲线来自既有目标速度曲线,或由现有的移动闭塞信号系统生成。目标速度曲线是关于位置的速度序列,可以将它视作一个分段函数,表达式为v=f(s)。
首车的目标曲线是关于位置的速度序列,参考曲线的生成方式为

2.2.2 后车的参考曲线设计

用类似于式(10)的方式,可以得到后车在k时刻的参考曲线为

2.2.3 控制方法具体流程
最终控制方法框架见图4,控制方法主体为MPC方法,具体步骤如下:

图4 控制方法框架
Step1得到本车上一时刻的预测状态序列Xf,若本车为编队中的首车,那么得到目标曲线信息R,否则得到前车的上一时刻的预测状态序列Xl。
Step2自适应机构根据式(10)和式(12)生成参考曲线序列Y,Y由速度信息Vref和位移信息Sref组成。
Step3由参考曲线序列Y建立2.3节所述优化问题,并求解得到控制序列U,并得到更新后的预测状态序列。
Step4将控制序列U中的第一个元素u(k|k)应用于本车的控制。
2.3 优化问题设计
为实现2.1节所提出的编队运行控制目标,分别对编队中的首车和后车分别设计优化问题的代价函数和约束。
2.3.1 首车的代价函数和约束
首车的责任是带领列车编队跟踪既定的目标速度曲线,因此首车的控制目标是在满足约束的情况下,尽可能跟踪参考曲线,最小化控制误差,代价函数为
minJ=Kv‖Vref-V‖2+Ku‖U‖2+Kf‖WU‖2
(13)
式中:Vref为由式(10)得到的参考曲线值,也是速度追踪的目标;V为本车各质点的速度信息,来自状态矩阵X;Kv,Ku,Kf分别为速度追踪、控制量、牵引制动变化率的权重系数,Kv为直接的控制效果,Ku为对节能和牵引制动平稳的考虑,Kf为对牵引制动率的考虑。优化问题由代价函数和约束组成,约束有以下几类:
1)动力学约束:由式(9)可以得到系统的动态方程等式约束

(14)
记为约束集Ω1,有X∈Ω1。
2)状态约束:列车运行过程中受到线路静态或临时限速的影响。vline为线路限速,它与目标速度曲线类似也是预设的位置-速度对,表现为分段函数
0≤V≤vline
(15)
记为约束集Ω2,有X∈Ω2。
3)控制约束:列车运行过程中,牵引制动力受牵引制动特性约束。控制约束本质上是控制量和速度状态量的联合约束
Ubmax≤U≤Utmax
(16)
记为约束集Ω3,有U∈Ω3。
4)变化率约束:由于重载列车牵引制动变化平缓的控制特点,最优控制应考虑对变化率进行约束,可对预测域中的Δu进行约束,但考虑控制器响应的快速性,第一个预测时刻约束取值可大一些。
|WU|≤ΔFmax
(17)
记为约束集Ω4,有WU∈Ω4。
2.3.2 后车的代价函数和约束
后车作为编队中的主要对象,它要保持和前车的间隔,维持和前车相同的速度,满足安全约束,建立代价函数为

后车还遵守安全约束,表示后车和前车之间存在最小行车间隔,以保持安全。前后车间隔始终大于安全间隔Dsafe为

2.4 线性化处理
本文在2.3节中,建立了首车和后车的控制优化问题,但其中存在非线性项和无解析式项,控制优化问题难以得到可行的最优解。在本节中这些非线性项和无解析式项进行处理,将优化问题转化为混合整数的二次优化问题,进行求解。
在优化问题中,在约束集Ω1中基本阻力表达式是二次的,这不利于优化问题的求解,因此对其做一阶泰勒展开,使之线性化。
首车的参考速度R,约束集Ω1中Fr、Fg和约束集Ω2中的vline都为非线性且无解析式的项,因此以分段函数的形式表达。以y为因变量,s为自变量,用符号S0,S1,…,Sn-1将s划分为不同区间,符号y0,y1,…,yn-1表示y在不同区间上的取值,那么分段函数可表示为
通过可以引入0-1指标变量Z0,Z1,…,Zn可以将这些非线性无解析式的项变成约束,则式(21)可转化为
只要满足z0+z1+…+zn=1∩G→∞,则式(22)恒成立(G为一个实数)。在约束集Ω3中,Ftmax,Fbmax是自变量为速度v的分段函数式(4)和式(5),用同样的方式可以处理。
通过式(22)原问题中的目标函数和约束集Ω1,Ω2,Ω3进行了线性化分段近似处理,优化问题转化为混合整数的二次优化问题进行求解。
3 仿真验证
本文通过数值仿真验证所提控制方法的有效性。为突出所提出方法的先进性,本文选择了自适应巡航控制(adaptivecruisecontrol,ACC)方法与本文提出的MPC方法进行对比。
自适应巡航控制是最早被提出的巡航控制方法之一,目前广泛应用于公路车辆自动驾驶系统的纵向速度控制。ACC控制器是线性状态反馈控制器[21],根据前后车辆的相对运动状态反馈形成控制律。一般,状态反馈形式的ACC控制律为


3.1 仿真设置
重载列车编队由三列万吨列车组成,编号为Train1、Train2、Train3。编队的首车Train1采用本文提出的MPC方法进行仿真,编队中的其余列车分别采用本文提出的MPC方法和ACC进行仿真比较,以体现本文方法的先进性。
编队列车初始速度为73.3km/h;初始位置分别为285、 283.5、 282km;仿真时间2 000s。列车选择朔黄铁路线路中编组最多的“1+1”组合式万吨编组列车,机车类型为HXD1+HXD1,车辆类型为C80。车辆参数和控制方法参数取值如表1所示。

表1 车辆参数和控制方法参数取值
表1中ml、c0l、c1l、c2l分别为HXD1型电力机车的质量以及基本阻力经验系数;mw、c0w、c1w、c2w分别为C80车辆的质量以及基本阻力经验系数;Ddes为列车追踪过程中的理想间距。在仿真开始时刻,编队中任意相邻两列列车车头车尾之间相隔Ddes。由于代价函数中各项单位数量级差距较大,参数Kv、Ks、Ku、Kf的取值数量级差距较大。
本文选取了朔黄重载线路某一平缓区段线路数据,线路全长50km,最高限速为80km/h。根据上述列车编组数据和线路数据,在满足约束的情况下,以代价函数式(13)和式(18)为目标,通过对列车编队运行过程的优化问题进行滚动优化,得到每一时刻编队中列车的控制量。
3.2 数值分析
本文以仿真过程中的速度误差和间隔误差评价控制方法的控制精度。图5显示了列车编队各列车的速度变化情况。编队首车以既有列车的LKJ运行数据作为目标曲线(ref)。
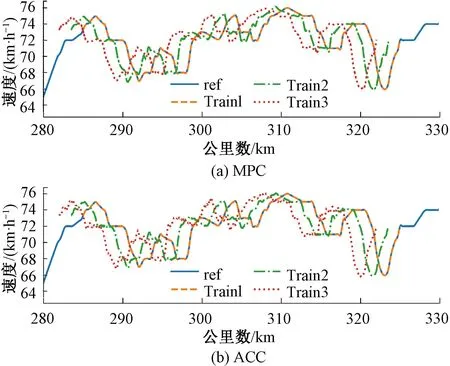
图5 速度位置曲线
图6为Train2和Train3的速度误差时间曲线。由图6可知,MPC方法的速度误差显著小于ACC方法,编队列车在同一时刻基本保持了相同的速度。但ACC方法相比于MPC方法存在更多的震荡,且第三列车的震荡程度略大于第二列车。

图6 速度误差时间曲线
图7为列车编队中Train2和Train3的间隔误差时间曲线,可以看出无论MPC方法还是ACC方法,都能较好的保持列车编队队形。ACC方法的间隔误差在一定范围内震荡,而MPC方法的列车编队间隔误差始终存在收敛趋势。

图7 间隔误差时间曲线
图8为MPC方法和ACC方法仿真下Train2和Train3的误差分布的核密度估计。核密度估计是在概率论中用来估计未知的密度函数,属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。从仿真列车编队的速度和间隔误差的核密度估计图形上可以看出,MPC方法下误差聚集在0附近,而ACC方法的误差数据比较分散。这说明MPC方法的控制精度更高,控制效果更好。

图8 速度误差和间隔误差分布
比较ACC和MPC两种方法的仿真结果,MPC的误差收敛性较好,从误差分布图像上看,速度误差和间隔误差在0附近聚集,且列车编队间隔始终满足安全约束,验证了该方法在坡度影响下速度变化时处理间隔约束的有效性。而ACC方法在仿真过程中,误差存在震荡现象,且Train3的震荡程度大于Train2,说明误差震荡的现象可能随列车编队延伸的方向放大,不利于编队长度的进一步增加。
两种方法的具体仿真结果见表2和表3,表中各项数据为绝对值。仿真结果说明本文提出的控制方法与既有的ACC方法相比,控制误差更小。

表2 MPC仿真结果

表3 ACC仿真结果
4 结论
本文针对重载列车载重大、编组长、操控难度大的特点,提出了一种重载移动闭塞系统下基于改进MPC的重载列车编队运行控制方法。本文首先建立了基于多质点模型的分布式控制结构的重载列车编队模型,然后通过增加自适应反馈环节改进MPC方法,并引入0-1指标变量处理非线性函数,进一步求解混合整数的二次型优化问题,最后采用朔黄重载移动闭塞系统下的实际线路数据和列车数据进行仿真,并与ACC控制方法进行了对比,仿真结果显示,所提出的改进MPC方法在误差收敛性、控制精度方面略优于ACC方法,且采用基于改进MPC的重载列车编队运行控制方法,在仿真平台上可得到最大速度误差为0.465 km/h,最大间隔误差为1.899 m,且误差分布聚集在零点附近。仿真结果表明:本文提出的基于改进MPC控制方法能够满足重载移动闭塞系统下编队控制精度要求,该控制方法是有效的。

