基于北斗3号PPP-B2b信号的实时精密单点定位方法研究
邓陈喜,姜 维,2,3,王 剑,2,3,蔡伯根,2,3
(1.北京交通大学 电子信息工程学院,北京 100044;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;3.北京市电磁兼容与卫星导航工程技术研究中心,北京 100044)
铁路技术创新是驱动铁路交通高质量发展的原动力。北斗卫星导航系统在铁路应用的标准化和产业化,能够为铁路运行的数字化、信息化、智能化管理提供更加科学、便捷的服务,从而提升铁路运输质量和维护效率,推动铁路产业与北斗产业融合发展。列车运行控制系统(以下简称“列控系统”)是确保行车安全和提高行车效率的关键技术设备,精确可靠的列车位置是列车超速防护和间隔控制的基础[1]。随着运输效率的提升和列车发车间隔的缩短,列控系统对高精度定位的需求逐渐增大。传统的列控系统采用轨道电路和计轴器确定列车位置,造价较高并且只能确定列车占用区段。北斗卫星定位技术为列车定位提供了新的技术方案,基于卫星导航的列车定位技术一方面能够实现列车精准定位,另一方面能够减少轨旁设备,降低相关设备的建设、运营和维护成本,对于发展低成本、高安全的列控系统具有重要意义。
目前,北斗卫星导航系统在铁路勘察测量、建造施工及运营维护等方面的应用以差分方式为主,主要使用RTK(real time kinematic)技术。RTK使用双差方式消除误差的影响,不仅能获取最优至厘米级的高精度定位结果,还可实现实时动态定位,因此得到广泛的青睐。虽然RTK时延短、精度高,但列车运营里程长,在铁路沿线布置一定密度的差分基站,将增加工作量和运维成本。且RTK的适用性、可靠性及精度与卫星数量及其分布相关,初始定位至少需要5颗以上卫星,在地势环境不佳的区域,基站无法设立,可见卫星数也将受到影响而不利于测量。除此之外,基站与车载设备间还需要通信网络建立传输通道,若网络中断,系统的定位性能将无法达到铁路运输对安全及效率的要求。因此,融合了单点定位与差分定位优势的精密单点定位技术,近年来成为铁路卫星导航领域的研究热点。
基于PPP(precise point positioning)的列车定位方法采用IGS(international GNSS services)网站免费公布的精密轨道和钟差,对从卫星到车载卫星接收机的各项误差进行建模计算,并利用经校正补偿后的载波相位观测值实现列车的绝对定位。PPP相比于其他卫星定位方式的优势在于,在不架设地面基站的情况下,只需要一台双频卫星接收机就能实现高精度定位,操作简单,且不受列车运营里程的限制,减少系统搭建成本的同时提高了定位产品的便捷性。但由于IGS提供的精密星历和钟差存在相应延时,所以在列车不间断运行时,基于IGS精密产品的PPP无法实时提供列车的精确位置。之后,为能向全球用户提供实时定位服务,IGS推出了实时精密产品。但与之前的精密产品一样,均是通过网络发布,一个稳定的网络环境对其至关重要,较差的网络连接会影响校正数据的完整性,进而影响PPP的定位性能,且实时精密产品的成本要求限制了它的广泛应用[2]。
然而,随着北斗三期顺利组网完成,BDS-3(BeiDou-3 navigation satellite system)由GEO卫星播发的PPP-B2b改正信息可在中国及周边区域内提升基于广播星历的卫星解算结果的精确性和连续性,从而实现实时精密单点定位[3]。由于BDS-3提供的PPP-B2b服务不需要接入互联网,因此在铁路沿线没有互联网连接或5G网络覆盖的地区,列车的精密单点定位也不会受到影响[4]。目前,PPP-B2b信号提供三种类型的改正数,其中,轨道和钟差改正数仅支持GPS和BDS-3(C19~C46),DCB(differential code bias)校正仅支持BDS-3。由于不同类型改正数的播发时间不同,轨道和DCB改正数的历元间隔为48 s,钟差改正数的历元间隔为6 s,轨道和钟差改正数各自配置了星历版本号和钟差版本号,以便互相关联对同一颗卫星的位置及钟差进行校正[5]。
2019年12月27日,PPP-B2b信号的接口文件公布[5]。REN等[2]、黄伦文等[3]、NIE等[6]、宋伟伟等[7]均是基于多个iGMAS测站的观测数据进行基于PPP-B2b信号的PPP性能分析。YANG等[8]基于武汉JFNG、WUH2测站的观测数据验证了PPP-B2b服务取代IGS RTS的可能性。LIU等[9]、TAO等[10]基于多个IGS MGEX测站的观测数据验证了在中国周边区域,PPP-B2b实时产品对BDS-3的准确性、可用性、完整性优于WHU及CENS产品。大多数学者选择测站的观测数据对基于PPP-B2b信号的PPP性能进行分析。王亚锋等[11]研究了基于PPP-B2b信号的实时PPP在快速静态标定上的应用。朱恩慧等[12]、肖浩威等[13]等进行了基于PPP-B2b信号的静态和仿动态实时PPP研究。但评估PPP-B2b服务在移动载体上的应用研究还较少。
本文提出一种基于PPP-B2b改正数的实时列车PPP算法。利用卫星接收机接收的PPP-B2b信号改正数进行精密产品恢复,再结合实际应用中测量得到的北斗卫星观测文件,分析PPP-B2b信号的轨道和钟差修正量级,最终以武汉大学MGEX(multi-GNSS experiment)最终精密产品WUM.FIN(Wuhan University MGEX final product)为参考,对比基于PPP-B2b改正数和超快速精密产品WUM.ULA(Wuhan University MGEX ultra-rapid product)的实时PPP定位测速精度与收敛情况。
1 基于精密星历的PPP
如表1所示,定位所需的卫星位置及钟差可通过表中5种星历处理得到。其中,广播星历用于单点定位中的卫星位置及钟差解算。在精密单点定位中,目前最普遍的方法是通过精密星历获取精度更高的卫星位置及钟差。而在精密星历中,只有超快速精密星历的预测部分可用于实时定位解算,其他均使用后处理方式。但基于铁路运输不间断运行的特点及其需联网下载的要求,将超快速精密星历用于实时列车定位仍存在局限。
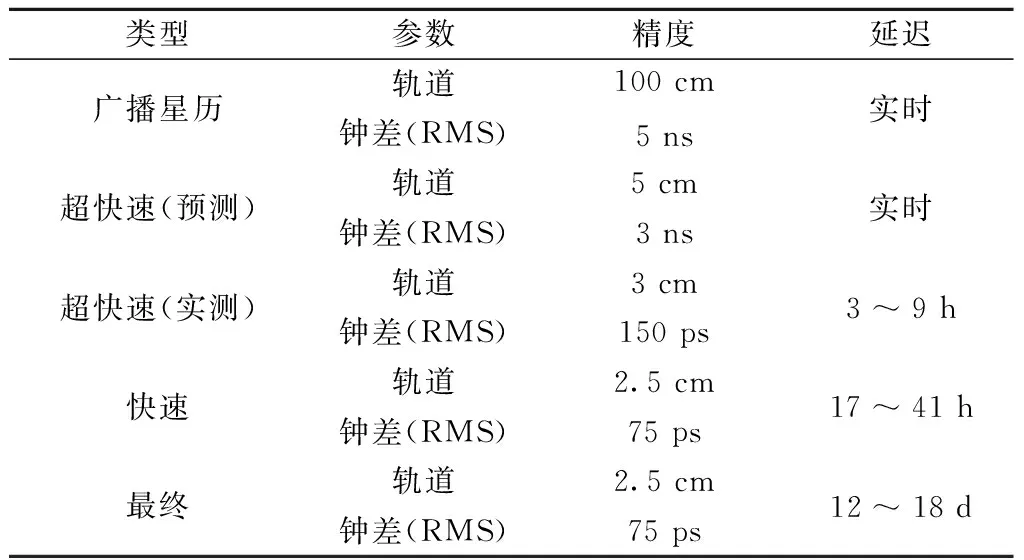
表1 IGS主要精密星历分类及其有关信息
1.1 主要误差及校正模型
为了消除相对论效应、大气延迟等影响,必须对载波相位或伪距观测值进行修正,这些误差的影响可达数米,即使在米级精度的伪距定位也需考虑。而在精密定位中,由于精密单点定位不使用差分方式,所以最重要的是考虑在差分定位下没有考虑的影响,如表2所示。

表2 精密单点定位主要误差及校正模型
1.2 数学模型及计算过程
精密单点定位以载波相位及伪距率观测方程为基础建立数学模型。以n颗可见卫星中的第i颗卫星为例,载波相位Φi及伪距率Di的观测方程为

(1)
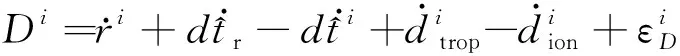
(2)
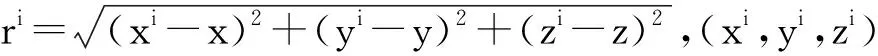

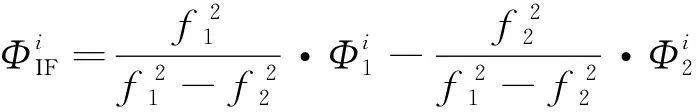
(3)

(4)
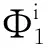
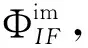
(5)
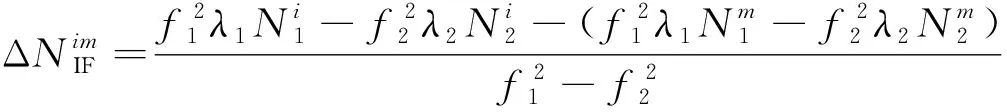
(6)
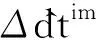

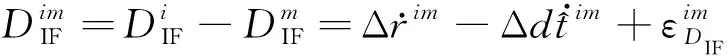
(7)

对于最终观测方程中的对流层延迟Δdtrop,可将其表示为
Δdtrop=ΔddryMdry(θ)+ΔdwetMwet(θ)
(8)
式中:Δddry、Δdwet分别为干、湿分量;Mdry(θ)及Mwet(θ)为干、湿分量对应的投影函数,可选择GMF模型[21];Δddry的计算可用Saastamoinen模型[18];Δdwet不易通过建模进行计算,将其作为之后滤波的状态估计量。
最后,进行卡尔曼滤波估计,构建系统的状态向量Xk为
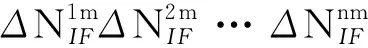
(9)
其中,每个历元的列车位置、速度及加速度状态分别由(x,y,z)、(vx,vy,vz)及(ax,ay,az)表示。
卡尔曼滤波离散形式的状态方程为
Xk=Fk-1·Xk-1+ωk-1
(10)
式中:Fk-1描述系统从Xk-1到Xk的状态转移过程;ω为模拟运动状态中的噪声矩阵,ω满足正态分布,即ω~N(0,Q),Q为ω的协方差矩阵。
为具体描述系统的状态转移过程,需对列车的运动状态进行分析后,选择恰当的概率模型进行模拟。在此,使用离散的一阶马尔可夫过程对列车运行过程中加速度的变化Pk进行建模,即
Pk=α·Pk-1+ωa,k-1
(11)
使用离散的随机游走过程对模糊度和对流层湿分量延迟的变化进行建模[20]
Δdwet,k=Δdwet,k-1+ωΔdwet,k-1
(13)
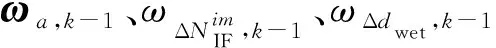
卡尔曼滤波量测方程为
Zk=Hk·Xk+νk
(14)
式中:Hk为系统状态估计Xk与量测输入Zk的线性关系;νk为系统量测噪声矩阵,νk满足正态分布,即νk~N(0,R),R为νk协方差矩阵。
系统的量测输入为
量测更新中R表示为[22]
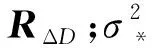
2 基于PPP-B2b的实时PPP
2.1 PPP-B2b修正模型
基于PPP-B2b的实时精密单点定位方法中更高精度的卫星位置及钟差是通过PPP-B2b改正数对由广播星历参数计算所得结果进行修正得到。
2.1.1 轨道修正
PPP-B2b轨道改正数中包含3种信息:IODCorr,在之后的钟差修正中使用;IODN需与BDS-3CNAV1导航电文中的IODC匹配成功;径向、切向及法向的改正数δOr、δOa及δOc,需通过旋转矩阵λ变换至ECEF坐标系下,方能得到ΔX。
ΔX=[λradialλalongλcross]·δO
(18)

Xprec,b2b=Xbrdc-ΔX
(19)
式中:Xprec,b2b为由PPP-B2b轨道改正数修正得到的卫星位置。
2.1.2 钟差修正
PPP-B2b钟差改正数中包含2种信息:IODCorr需与PPP-B2b轨道改正数中的IODCorr匹配成功,方能将钟差改正数与轨道改正数组合对该历元下用广播星历解算出的卫星位置和钟差进行修正;钟差改正数C0需通过除以真空中的光速c,与广播星历解算出的卫星钟差dtbrdc保持同一单位,计算得到实时钟差结果。由PPP-B2b钟差改正数修正得到的卫星钟差dtprec,b2b为
dtprec,b2b=dtbrdc-C0/c
(20)
在利用PPP-B2b改正信息恢复精密钟差时,可能出现某时刻轨道与钟差修正信息中两个IODCorr不相同的问题,一种解决方法是使用与轨道改正数匹配的钟差改正数,由于钟差改正数很快就会更新,因此对定位精度影响很小[23]。
2.1.3DCB校正
若卫星i在卫星时钟的t时刻开始产生测距信号,在标准时间的T时刻测距信号到达接收机,并被接收机接收,那么该卫星的钟差dti应为
dti=(t+b+dtc)-T
(21)
式中:b为卫星内部时延,即信号在卫星端从产生到发出所经时间;dtc为测距信号的传播时间,下角c为光速。
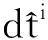
PPP-B2b信号中播发的“DCB改正数”是指各系统测距信号与钟差基准信号B3I间的内部时延之差。PPP-B2b信号提供了多种类型的DCB改正数,包括B1I-B3I、B1C-B3I、B2a-B3I和B2b-B3I。通过这些DCB改正数,可以实现基于BDS-3的多频实时列车精密单点定位[23]。
2.2 基于PPP-B2b的实时PPP载波相位函数模型
基于PPP-B2b的实时PPP载波相位函数模型为
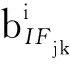
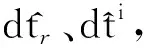
则基于PPP-B2b的实时PPP载波相位函数模型可改写为
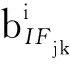
式中:fj及fk分别为双频信号j和k的频率;bj及bk分别为双频信号j和k在卫星端的内部时延;DCBB1I-B3I为B1I与B3I信号的时间偏差。
若P为伪距,则有
故伪距率无电离层组合观测值为
2.3 基于PPP-B2b的实时PPP流程
由于PPP-B2b修正是针对于广播星历的解算结果,而导航电文也是相对于天线相位中心,所以无需考虑天线相位中心改正。针对主要误差项采取对应模型进行误差补偿,采用经星间单差处理后的无电离层组合观测值作为系统的量测输入,最后通过卡尔曼滤波实时得到列车的位置、速度及加速度,具体计算过程见1.2节。整个基于PPP-B2b信号的实时PPP流程见图1。
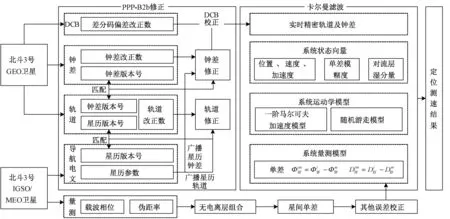
图1 基于PPP-B2b信号的实时PPP流程
Step1卫星接收机获取北斗三号卫星的CNAV1导航电文和原始观测数据信息。根据接收到的星历参数(包括18个开普勒轨道参数)计算相应卫星(实际是卫星天线相位中心)位置坐标和钟差。
Step2根据这一时刻卫星在广播星历中的星历版本号,在PPP-B2b轨道改正信息中找到IODN与之匹配且在轨道有效期96 s内的轨道改正数,再根据PPP-B2b轨道改正数中的钟差版本号IOD Corr,在PPP-B2b钟差改正信息中找到与之匹配且在钟差有效期12 s内钟差改正数,最终得到卫星在该时刻的一组改正数。联合广播星历解算出的卫星位置、速度及钟差,按照式(19)式(20)可得实时精密轨道和钟差。为了实现各类信号同步处理,根据式(25),将PPP-B2b信号播发的码间偏差改正数中的DCBB1I-B3I改正数应用于实时卫星钟差校正。
Step3对载波相位及伪距率观测量进行双频组合、星间单差等操作,并按照表2中所述校正模型及对流层模型对量测输入进行补偿,并以列车三维位置、速度和加速度、所用卫星模糊度和对流层湿分量延迟作为状态向量,以组合观测值的单差作为量测进行滤波估计,最终得到列车的定位测速结果。
3 实验过程及数据分析
3.1 实验描述
为了评估基于PPP-B2b的实时精密单点定位方法在实际应用中的定位效果及未来铁路应用中的可行性,采用2022年1月和4月的车载设备动/静态数据进行实验,并在PPP-B2b的修正量级及实时PPP测速定位方面分别对动/态实验结果进行分析。实验结果的参考数据由千寻差分定位提供。实验全程利用飞纳接收机FRⅡ-Plus Receiver接收PPP-B2b改正数及实验所需载波相位和伪距率等观测量,以0.1 s为时间间隔,采集时长为20 min。
动态实验的载体运行轨迹及速度见图2,静态实验的载体状态信息见图3。在整个实验时间内,动、静态实验的观测卫星分别为5颗和6颗,在对观测量进行星间单差后,变为4颗和5颗,均满足精密单点定位条件。水平位置精度因子HDOP(horizontal dilution of precision)表示卫星空间分布对水平定位精度的影响,NDOP、EDOP分别表示HDOP在北、东方向的分量,计算式为[24]
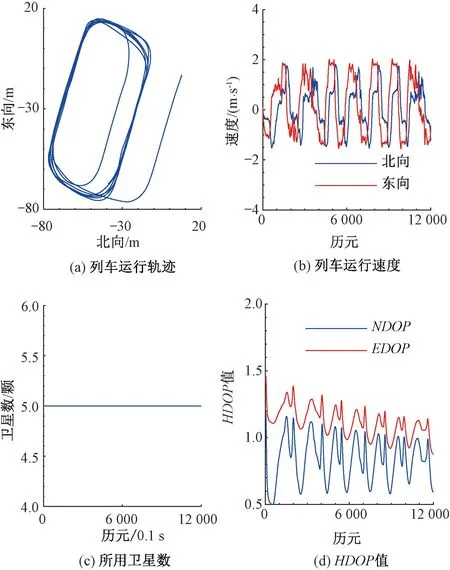
图2 动态实验载体运行轨迹及速度
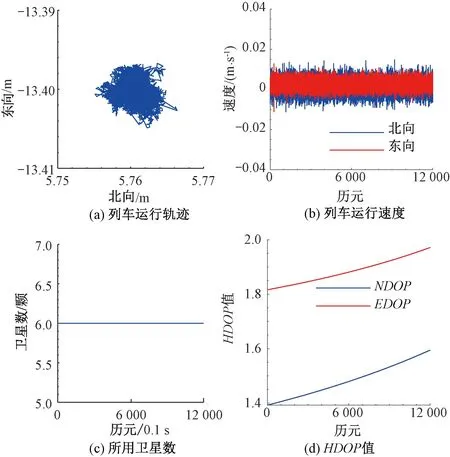
图3 静态实验载体状态信息
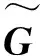
式中:αi和θi分别为卫星的方位角和仰角。
(33)
理论上,HDOP值越接近1,卫星空间分布越接近最佳几何构型[25]。
动态实验对应的NDOP值和EDOP值在1附近波动,说明动态实验的卫星空间分布较佳;静态实验对应的NDOP值和EDOP值均呈上升趋势,最大值不超过2,说明卫星空间分布随时间推移在改变,定位初始时刻的卫星空间分布最佳。
3.2 PPP-B2b轨道及钟差修正量分析
3.2.1 轨道修正量分析
PPP-B2b轨道改正数直接给出在RAC坐标系(径向:R;切向:A;法向:C)下广播星历解算出的卫星位置的修正量,按照式(21)可得到ECEF(earth-centered,earth-fixed)坐标系下的修正量见表3。
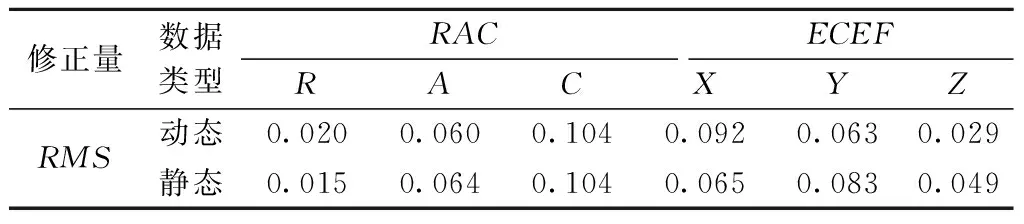
表3 B2b轨道修正量的平均RMS m
1)动态数据
在动态数据中,PPP-B2b在RAC坐标系下轨道修正量的均方根RMS见图4(a),在ECEF坐标系下轨道修正量RMS见图4(b),图中横坐标为卫星的伪随机码(pseaclo random noise code, PRN)。


图4 动态数据B2b轨道修正量RMS
如表3所示,PPP-B2b对轨道的修正量在RAC坐标系下量级为厘米级和分米级,其中,C方向的修正量相对较大,主要在0.103 8 m左右,R方向的修正量相对较小,主要在0.020 1 m左右。
如表3所示,PPP-B2b对轨道的修正量在ECEF坐标系下量级为厘米级,其中,X方向的修正量相对较大,主要在0.092 2 m左右,Z方向的修正量相对较小,主要在0.029 2 m左右。
2)静态数据
在静态数据中,PPP-B2b在RAC坐标系下轨道修正量的RMS见图5(a),在ECEF坐标系下轨道修正量的RMS见图5(b)。
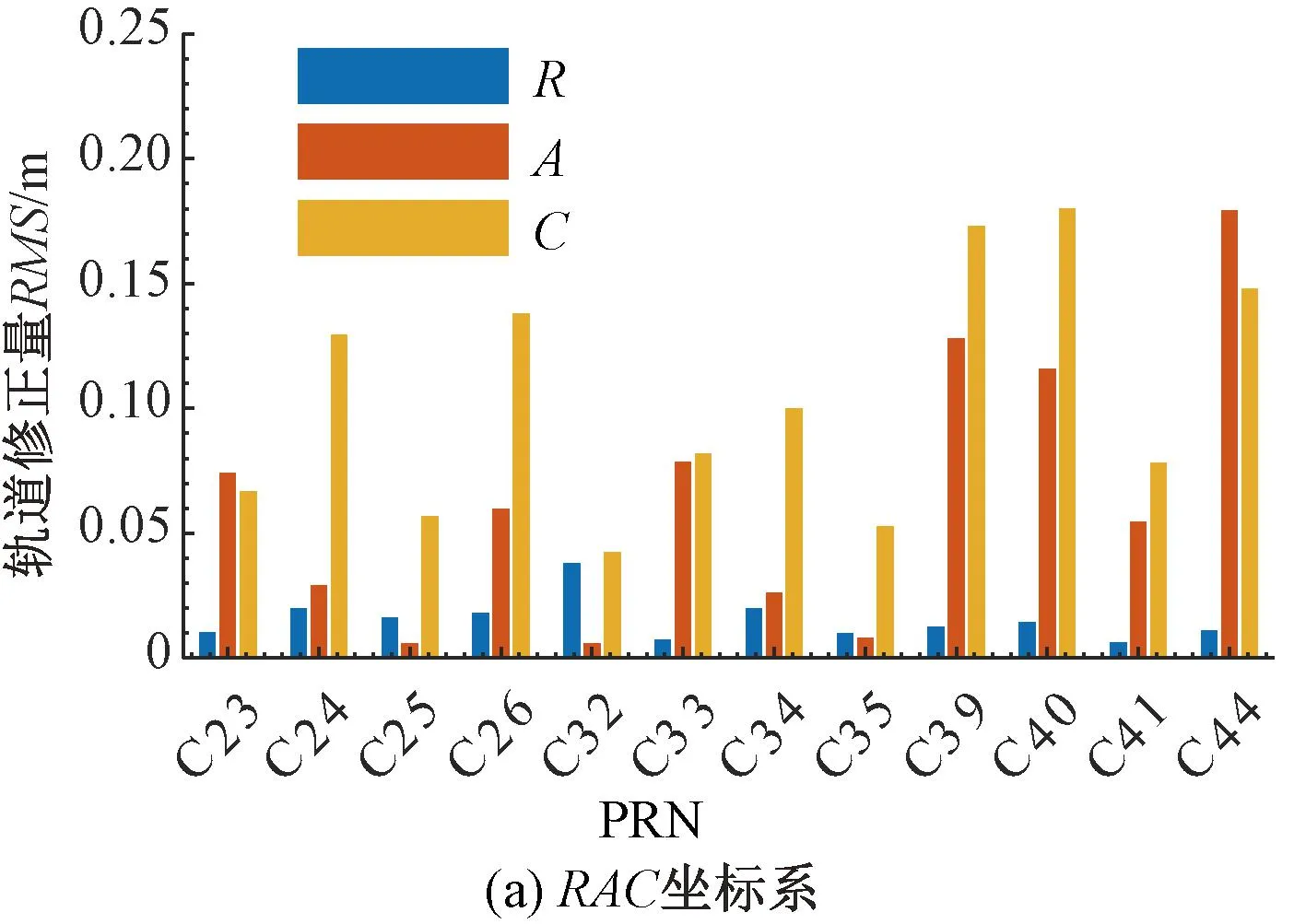

图5 静态数据B2b轨道修正量RMS
如表3所示,PPP-B2b对轨道的修正量在RAC坐标系下量级仍在厘米级和分米级,其中,C方向的修正量相对较大,主要在0.103 9 m左右,R方向的修正量相对较小,主要在0.015 3 m左右。
如表3所示,PPP-B2b对轨道的修正量在ECEF坐标系下量级仍在厘米级,但不同于动态数据,Y方向的修正量相对较大,主要在0.082 6 m左右,Z方向的修正量相对较小,主要在0.049 2 m左右。
对比动态数据与静态数据的结果,发现在RAC坐标系下,C方向修正量整体大于其他方向修正量,在0.1 m左右,而R方向修正量整体小于其他方向修正量,均在0.05 m以下。而在ECEF坐标系下,Z方向修正量整体小于其他方向修正量,在0.5 m左右。
3.2.2 钟差修正量分析
1)动态数据
在动态数据中,PPP-B2b钟差修正量RMS见图6,DCB修正数对钟差的校正量RMS见图7。
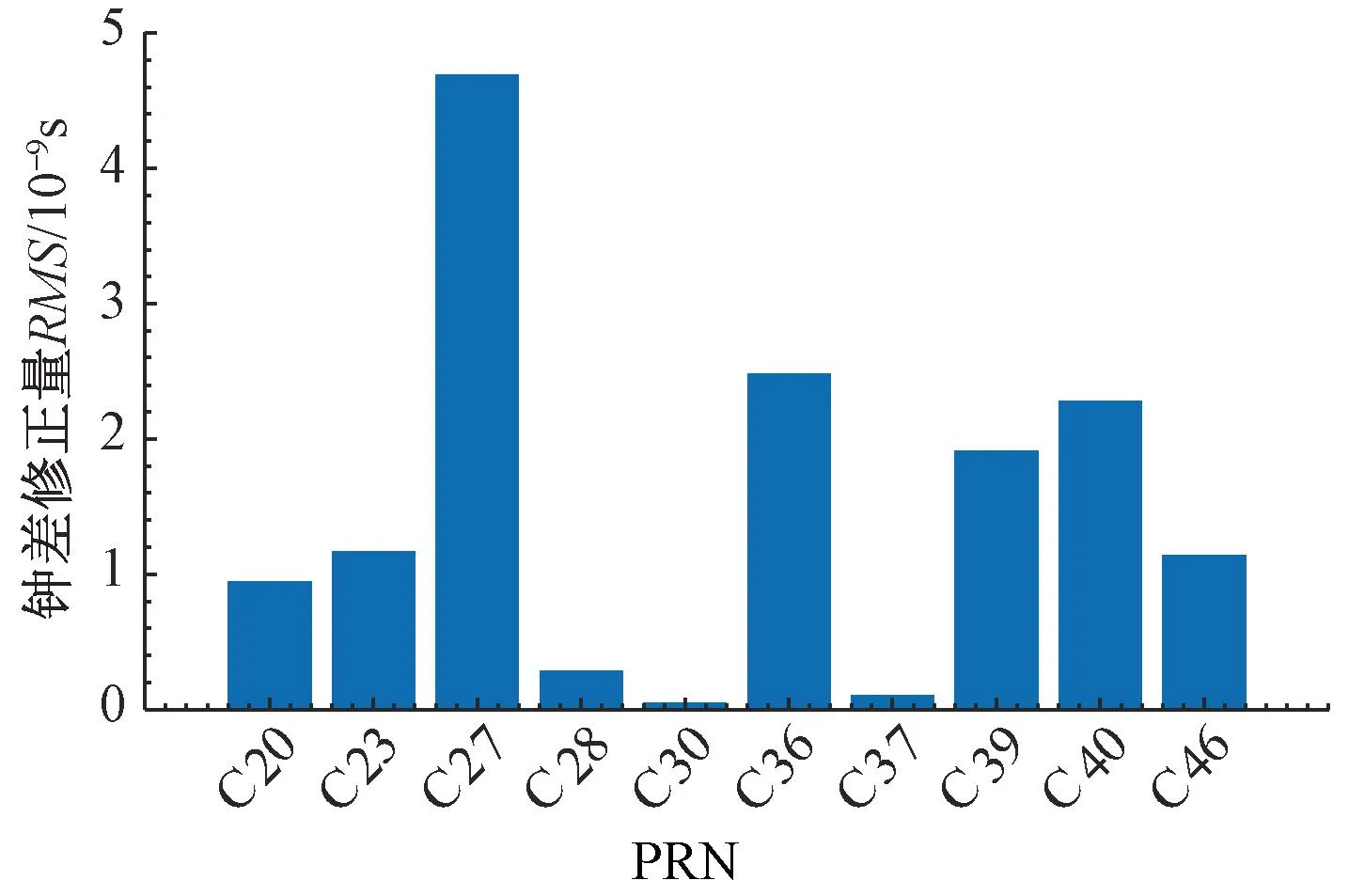
图6 动态数据B2b钟差修正量RMS

图7 动态数据B2b-DCB校正量RMS
图6和图7中,PPP-B2b钟差改正数的修正量级在纳秒,DCB改正数对钟差的校正量级比钟差改正数的修正量级高出一个量级,所以PPP-B2b对卫星钟差的修正量级在10-8s。
2)静态数据
在静态数据中,PPP-B2b钟差修正量RMS见图8,DCB修正数对钟差的校正量RMS见图9。
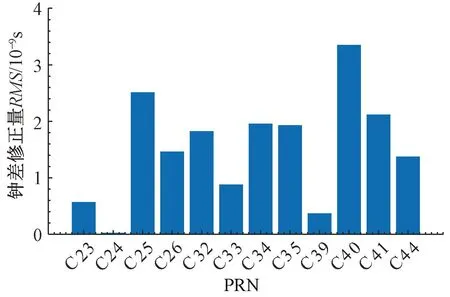
图8 静态数据B2b钟差修正量RMS
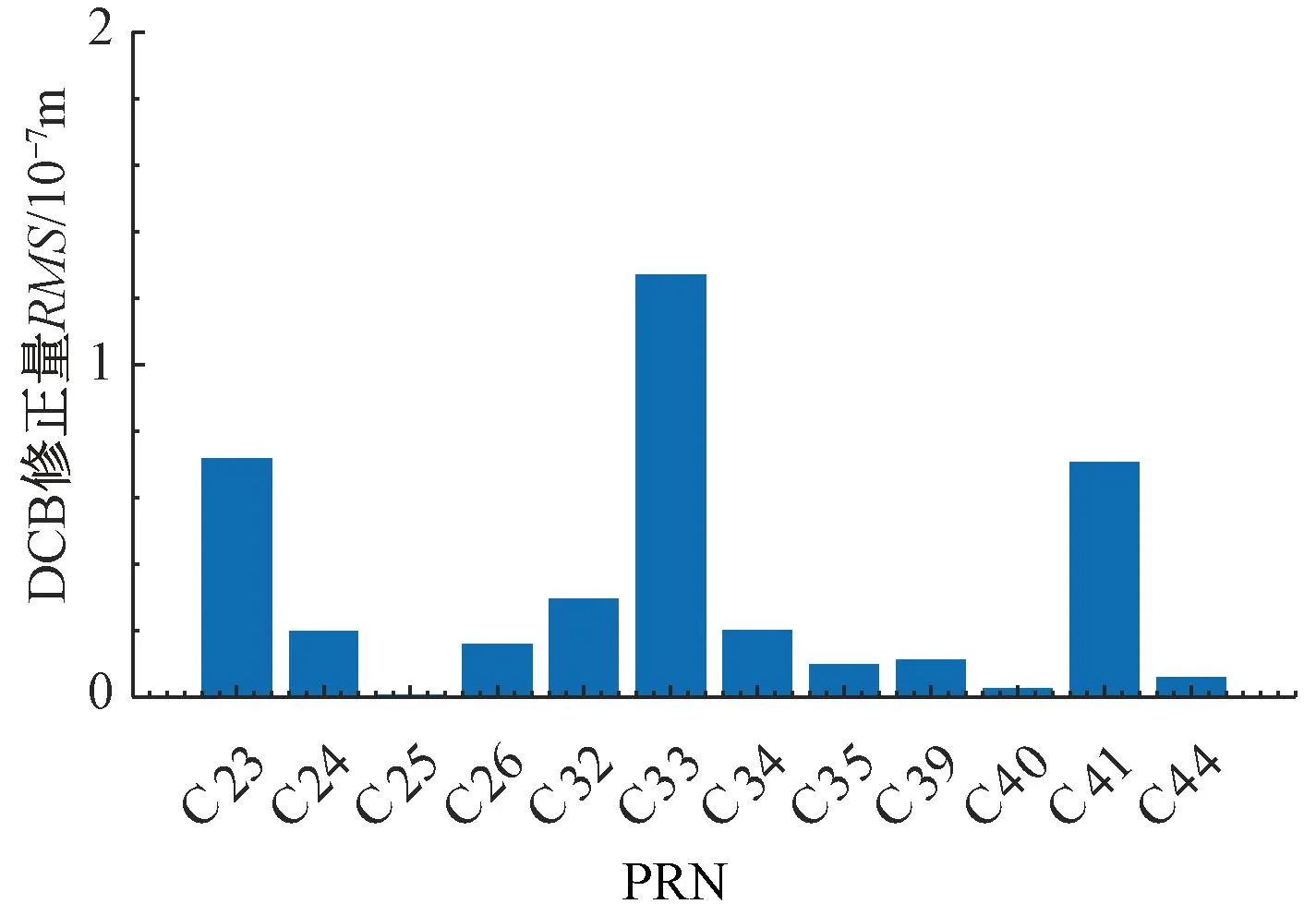
图9 静态数据b2b-DCB校正量RMS
图8和图9中,与动态数据中的结论相同的是,PPP-B2b钟差改正数的修正量级在纳秒,但与动态数据中的结论不同的是,大多数DCB改正数对钟差的校正量级比钟差改正数的修正量级高出一个量级,但极个别如C33(PRN为33的卫星)钟差校正量会比钟差改正数的修正量级高出两个量级,但仅为1.2×10-7s,所以大多数PPP-B2b对卫星钟差的修正量级仍在10-8s。
3.3 基于PPP-B2b的实时PPP结果分析
为了验证PPP-B2b实时PPP算法的可用性,选择WUM.ULA和WUM.FIN产品与利用PPP-B2b改正数恢复的精密产品的PPP定位测速结果比较。三种精密产品的动态PPP定位测速误差见图10和图11,静态PPP定位测速误差见图12和图13。
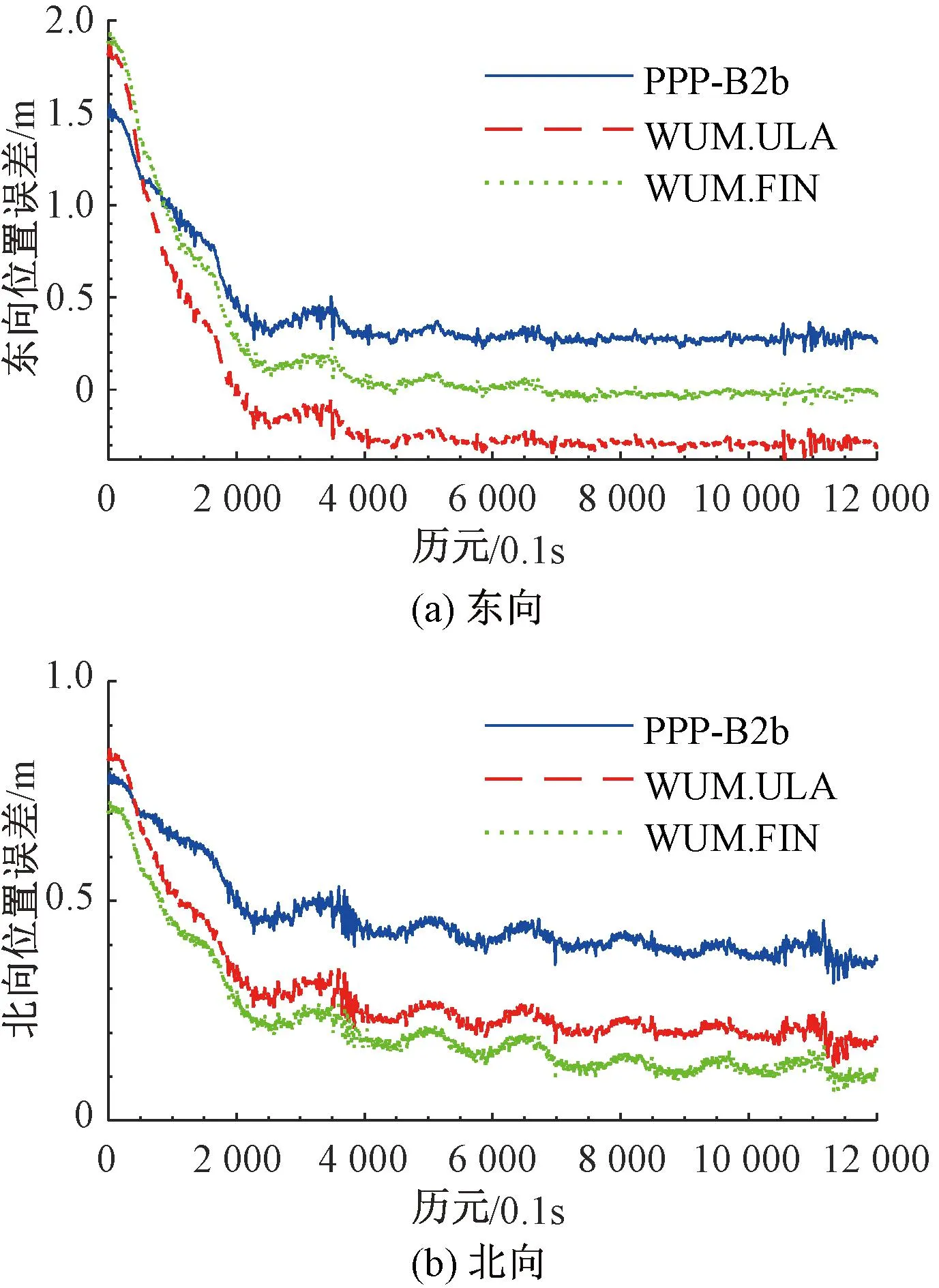
图10 动态PPP定位误差
图11 动态PPP测速误差
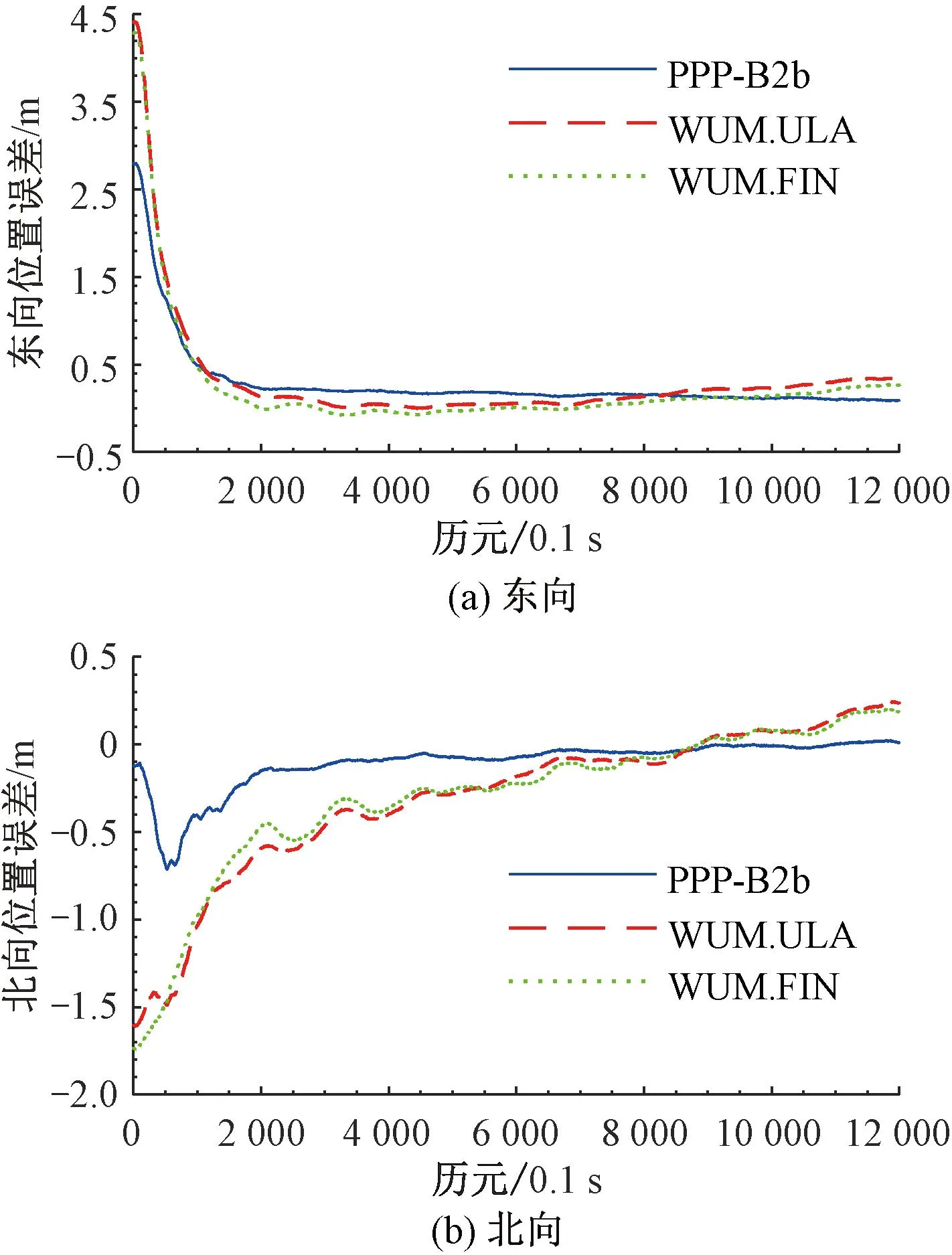
图12 静态PPP的定位误差
图13 静态PPP测速误差
1)动态数据
图10中,北向位置误差中,三种精密产品的误差曲线变化较为相似,都存在少许波动。PPP-B2b相对收敛速度较慢,收敛时间较长,WUM.FIN在2 000历元时已经收敛至0.27m,WUM.ULA收敛至0.34m,而PPP-B2b收敛至0.51m,在12 000历元时,WUM.FIN已经收敛至0.10m,WUM.ULA收敛至0.18m,而PPP-B2b收敛至0.37m。东向位置误差曲线变化与北向相似,虽然PPP-B2b相对WUM.FIN收敛时间较长,但其相比于WUM.ULA已经可以达到与之相同的定位精度,在0.2~0.3m附近波动。
整体来看,PPP-B2b的定位误差在0.3~0.4m之间,东北方向位置误差有些许差别,相差0.1m以内,由于能接收到PPP-B2b改正数的卫星数量有限,很可能是车辆移动过程中卫星的分布变化导致。
图11中,三种精密产品的速度误差变化相似,均在0.2m/s的范围内持续波动。由于三种精密产品的速度误差曲线在视觉上很难分开,为了更好地量化三种精密产品的动态位置速度误差,表4为基于PPP-B2b改正数恢复的精密产品、WUM.ULA产品与WUM.FIN产品三种精密产品的动态水平定位测速结果误差的对比。
如表4所示,WUM.FIN的位置速度误差RMS相对较小,在位置误差RMS中,PPP-B2b的定位误差RMS北向0.417 2m,东向0.304 1m,与WUM.ULA相差数厘米。在速度误差RMS中,PPP-B2b与WUM.ULA的速度误差RMS十分接近,相差小于0.01m/s。
2)静态数据
图12中,北向位置误差中,WUM.ULA与WUM.FIN变化相似,存在一定波动,PPP-B2b相对平稳,收敛时间相比动态要快,在1 200个历元时已收敛至0.5 m,在12000历元时收敛至厘米级。东向位置误差中,三种精密产品的位置曲线在前8 000个历元走向一致,WUM.ULA和WUM.FIN的收敛时间较短,在2 000个历元时,WUM.ULA收敛至0.13 m,WUM.FIN收敛至0.007 m,最终PPP-B2b相对平稳,收敛至0.08 m。
图13中,三种精密产品的静态速度误差曲线相比于动态速度误差曲线,变化幅度小,变化范围不超过0.01 m/s,且三种产品的速度误差相差不大。其中,比较水平方向的测速误差,东向的变化幅度更小。
表5为基于PPP-B2b改正数恢复的精密产品、WUM.ULA产品与WUM.FIN产品三种精密产品的静态水平定位测速结果误差的对比。

表5 静态PPP的定位测速误差RMS
在静态模式下,PPP-B2b的定位误差RMS在北向和东向分别达到0.100 5 m和0.174 1 m,北向的位置误差RMS优于WUM.ULA和WUM.FIN,东向的位置误差RMS优于WUM.ULA。而PPP-B2b的速度误差RMS已经与WUM.ULA和WUM.FIN在同一量级。
4 结论
本文提出一种基于北斗三号PPP-B2b服务的实时精密单点定位方法,实时高精度卫星轨道及钟差由PPP-B2b校正电文对广播星历解算的卫星轨道及钟差修正得到,最终基于PPP量测模型和扩展卡尔曼滤波与实测数据得到载体运行状态估计。将基于PPP-B2b服务的实时动/静态PPP结果分别与基于WUM.ULA服务的动/静态PPP结果进行对比,得出结论:在保证时效性的前提下,基于PPP-B2b服务的实时动/静态PPP可得到与传统基于IGS精密产品的PPP定位精度相当的定位测速结果,实现实时动/静态分米级定位、厘米级每秒测速。
现阶段本方法已在车载接收机上得到验证,后续本方法将在铁路列车定位方面进行实验验证。

