基于Wiener退化过程的动车组部件状态-机会维修模型分析与研究
皇甫兰兰,苏宏升,林俊亭
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
高速动车组以电力为动力,具有节能环保的优点。然而,随着动车组运行速度的提高和载客量的增加,高速动车组在方便人们出行的同时,也出现了一些问题,如可靠性和安全性面临巨大挑战、维修费用成本逐年增加等。因此,研究和分析动车组的可靠性和维修问题具有重要的理论意义和工程应用价值。
预防性维修在大型设备如风电、能源、核电以及高铁等领域的应用和研究愈来愈受到学者们的关注。目前,系统或部件的维修主要有两种方式: 事后维修和预防性维修。预防性维修分为基于时间的维修(time-based maintenance,TBM)和基于状态的维修(condition-based maintenance,CBM)[1]。在建模过程中,TBM 模型是一种有计划的预防性维修活动,能够在确定的维修时间点安排相应的维修资源,实施后能够满足部件的性能要求,但其只考虑了运行时间对部件失效率的影响,没有考虑部件的真实运行状态,因此,存在“欠维护”和“过维护”的现象[2-3]。随着检测技术的发展,学者们提出了一些基于部件状态的预防性维修策略。文献[4]提出一种基于 Markov 特性的状态维修策略,能够根据部件的实际状态制定动态的维修策略。文献[5-6]建立基于比例失效模型的状态维修策略,根据多属性决策理论,建立联合目标函数。文献[7]根据动车组齿轮箱的实时运行情况,建立威布尔比例风险模型,得到了最佳维修时间和维修阈值。文献[8]基于SDE建立风力发电机齿轮箱的威布尔比例风险模型,并对影响齿轮箱状态的3个重要因素进行加权处理,得到最优的预防性维修周期。以上文献大多是在假设部件修复如新的条件下进行的研究,未考虑部件的不完全维修。而实际部件进行预防性维修后,部件的状态处于在“修复如新”和“修复如旧”之间,针对这一问题,文献[9]基于Gamma过程建立劣化系统的CBM模型,设备在进行预防性维护后考虑其维修的不完全性,制定相应的维修策略。文献[10]基于Wiener过程,提出一种牵引供电设备状态检修模型,考虑预防性维护和修复性维护后的不完全性,实现运行费用率最低的优化目标。但这些研究针对的是单一部件或者将多部件构成的系统看为一个整体进行的维修,未考虑部件之间的故障、经济等关联关系。
大型复杂系统中的各部件之间往往存在着一定的相关性,因此,基于串联部件的机会维修策略是一种有效减少维修费用的方法。国内外研究人员对于多部件机会维修策略进行了深入的研究。文献[11]研究在部件进行维修过程中,考虑其他部件的维修情况,确定机会维修的范围。文献[12]提出一种基于可靠性的机会预防性维修优化模型,引入机会维修的思想,通过偏最小二乘回归方法优化机会维修阈值,确定最佳预防性维修阈值和机会阈值。文献[13]引入动车组部件故障风险量化和机会维修里程窗的概念,建立部件的机会维修策略。上述文献,多数未考虑部件的检测状态对机会阈值的影响。文献[14]提出一种状态-机会维修(condition-based opportunity,CBOM)策略,该策略采用威布尔比例失效模型,但未考虑可修系统中存在的不完全维修。文献[15]针对维修过程中存在的不完全维修情况,借助维修因子描述部件的不完全维修,并利用维修因子的取值大小确定状态维修函数和机会维修函数,其针对的是符合威布尔比例失效模型的可修部件。本文针对动车组部件在运行过程中的劣化特性,利用Wiener过程描述部件的这种特性,借助指数分布的随机几何过程反映不完全维修后部件的劣化损伤程度。通过随机过程和拓扑的基本理论分析状态检测周期的大小与不同检测策略之间的关系。在求得各部件的最优状态阈值和维修检测周期的基础上,引入机会阈值与状态阈值的比值,建立状态-机会维修策略模型,并求得部件机会维修次数期望值的数学表达式,同时采用蒙特卡洛算法流程进行求解,确定各部件的最佳机会阈值,达到优化维修费用率的目标。通过算例进行仿真验证状态-机会维修模型在减少停机次数和降低维修费用率方面的有效性。
1 模型建立
1.1 模型概念描述

引理1令f(yi(t))为退化量yi(t)的连续函数,且二次可微,则存在一个随机函数
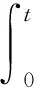

(1)
式中:β为退化量yi(t)函数的扩散参数。
证明:
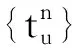
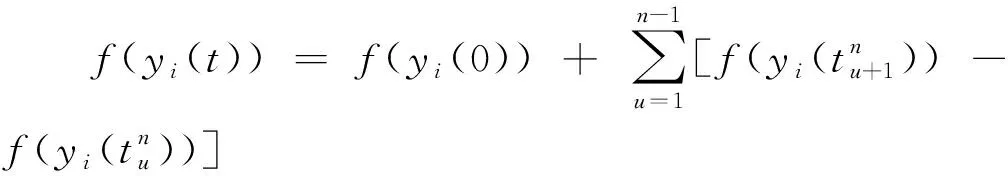
(2)
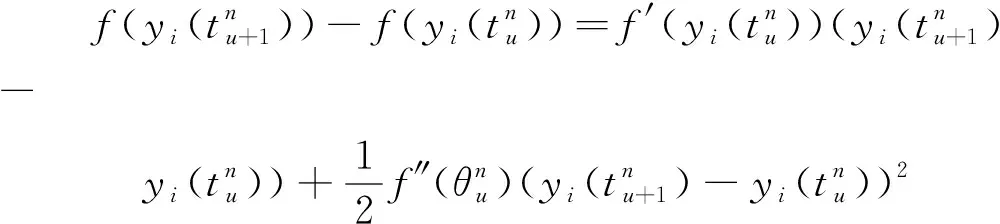
(3)

将式(3)代入式(2)可得
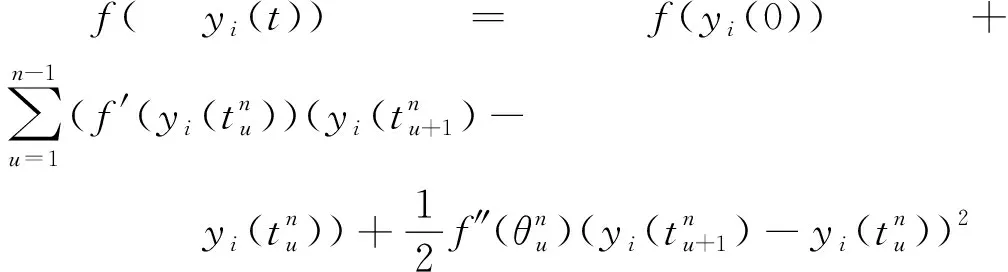
(4)
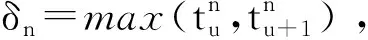
引理得证。
由引理1可以看出,δn为部件状态检测的时间间隔,反映了部件状态检测的稠密程度。当δn→0时,部件的状态检测视为连续检测。当δn为大于0的定值时,视为定期检测。
定义1以部件状态的故障阈值Di为约束条件,以费用率或可用度等为优化目标,以τ为参数空间T=[0, ∞)上的分割空间长度,而制定的预防性维护计划,定义为基于时间的维修。
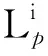
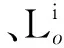
由定义1、定义2、定义3可知,CBM和OM实质上是部件在状态空间意义下的TBM。
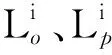


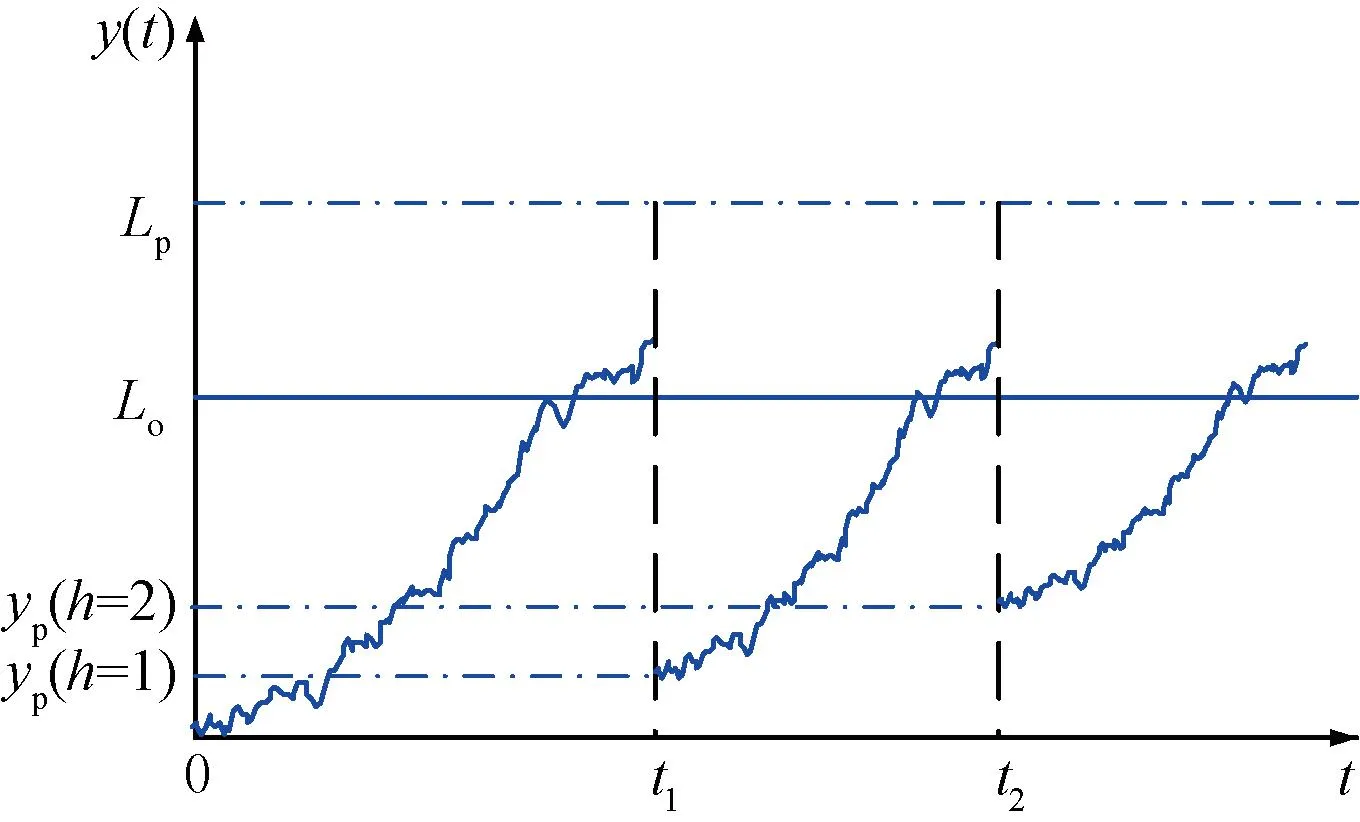
图1 动车组部件状态-机会维修策略
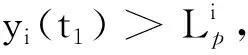

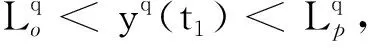
在时刻t1,3个部件的维修策略为:部件i、q同时维修,部件i进行状态维修,进行机会维修中的小修——更换零部件的不完全维修方式,部件j不维修,部件i、q同时维修只需花费一次固定维修费用,且减少停机一次。状态-机会维修策略在实施过程中,能否发挥应有的作用和效益,在于机会维修节约的维修费用(包括停机次数、停机成本、固定维修费用)与机会维修增加的成本(频繁的更换零件)之间的博弈,当实施状态-机会维修策略后,机会维修节约的维修费用大于机会维修增加的成本时,才有意义,反之,该维修策略意味着部件的过度维修或者维修资源的浪费,则意义不大。而对于大型设备动车组,状态-机会维修策略意义在于减少动车组的出入车辆库停检修次数,提高维修效率,降低停机损失成本。而多部件维修的有机结合,在一定程度上能够分摊固定维修费用,降低固定维修成本。
1.2 基于拓扑的模型分析
命题1设δ1、δ2为任意大于等于0,小于设计寿命TP的实数,且δ2=mδ1,m为正整数,则基于检测间隔δ1的CBM所建立的拓扑要细于基于检测间隔δ2的CBM所建立的拓扑。
证明:令检测间隔(δ1,2δ1,3δ1,…,iδ1,…,nδ1)所构成的集合为A,T1为集合A的拓扑,则有
T1={A⊆R|
∀iδ1∈A,∃i,n>0,
(δ1,2δ1,3δ1,…,iδ1,…,nδ1)⊆A}
令检测间隔(δ2,2δ2,3δ2,…,iδ2,…,nδ2)所构成的集合为B,T2为集合B的拓扑,则有
T2={B⊆R|
∀iδ2∈B,∃i,n>0,
(δ2,2δ2,3δ2,…,iδ2,…,nδ2)⊆B}
由于δ2=mδ1,m∈N,则有
集合B⊆A,由拓扑的定义及性质[16]可知,T2⊆T1,拓扑T2粗于拓扑T1(拓扑T1细于拓扑T2)。
命题得证。
从命题1可知,当δn→0时,部件为连续状态检测,所组成的拓扑为最细的拓扑。事后维修(passivemaintenance,PM)只在设备故障后方进行维修,是设备维修所构成的拓扑中最粗的拓扑,是平凡拓扑。TBM所构成拓扑是CBM所构成拓扑中最粗的拓扑。
推论1多部件的状态-机会维护CBOM所构成拓扑细于基于状态的维护CBM所构成拓扑。
证明:令CBM下检测间隔(δ1,δ2,δ3,…,δi,…,δn)所构成的集合为G,T3为集合G的拓扑,则有
T3={G⊆R|
∀δi∈G,∃i,n>0,
(δ1,δ2,δ3,…,δi,…,δn)⊆G}
令检测间隔和机会维修间隔(δ1,δ2,δ3,O1,…,δi,…,Oi,…,δn)所构成的集合为H,T4为集合H的拓扑,则有
T4={H⊆R|
∀δi,Oi∈H,∃i,n>0,
(δ1,δ2,δ3,O1,…,δi,…,Oi,…,δn)⊆H}
显然,集合G⊆H,由拓扑的性质可知,T3⊆T4,拓扑T3粗于拓扑T4(拓扑T4细于拓扑T3)。
推论得证。
由推论1可得,针对多部件的预防性维护,CBOM是CBM的一种优化策略。
1.3 不完全维修的Wiener退化模型
部件的退化过程一般都具有一定的随机性,基于随机过程刻画部件的退化过程中的不确定性是一种比较有效的方法[17]。为了便于分析与计算,随机退化模型多采用齐次平稳的增量过程,例如Gamma过程和Wiener过程。根据文献[18]研究,Gamma过程适合于符合非减的退化过程部件的描述。而Wiener过程模型比较适合于描述退化过程为非单调且呈增长趋势的部件,同时这种退化过程存在波动现象。针对动车组牵引供电系统三部件退化的特点,采用可线性化的Wiener过程模型建立部件的退化过程,令y (t)为部件在时刻t的退化量,可表示为
y(t)=y(0)+αΛ(t)+βB(Λ(t))
(5)
式中:y(0)为部件的初始退化量;α为漂移参数;β为扩散参数,假设每次预防性维修后的退化速率保持不变,则α和β为固定值,其值可以通过似然估计法[19]求得;Λ(t)为时间t的非负单调增函数;{ B(Λ(t)), t≥0}为标准一维布朗运动。根据Wiener的性质,且y(0)=0,易知退化量函数y (t)~N(αΛ(t), β2Λ(t)),N为正态分布。
根据式(5)求得的退化量y (t)为部件退化数据的拟合值,而动车组部件在运行过程中,受不同工况和零件的影响,其实际检测的退化量x (t)与拟合值y (t)必然存在一定的残差e (t),其计算式为
e(t)=|x(t)-y(t)|
该残差能够反映部件自身退化过程的不确定性以及随机测量误差中的不确定性。而残差正态性的频率检验方法能够检验模型的正确性以及适应性,进而采取相应的措施及时更新模型参数,以便模型更好地拟合实际退化量。
令D为部件退化的故障阈值,当部件的退化量y (t)超过D时,部件失效。根据可靠性定义,可求得部件的可靠度函数RD为
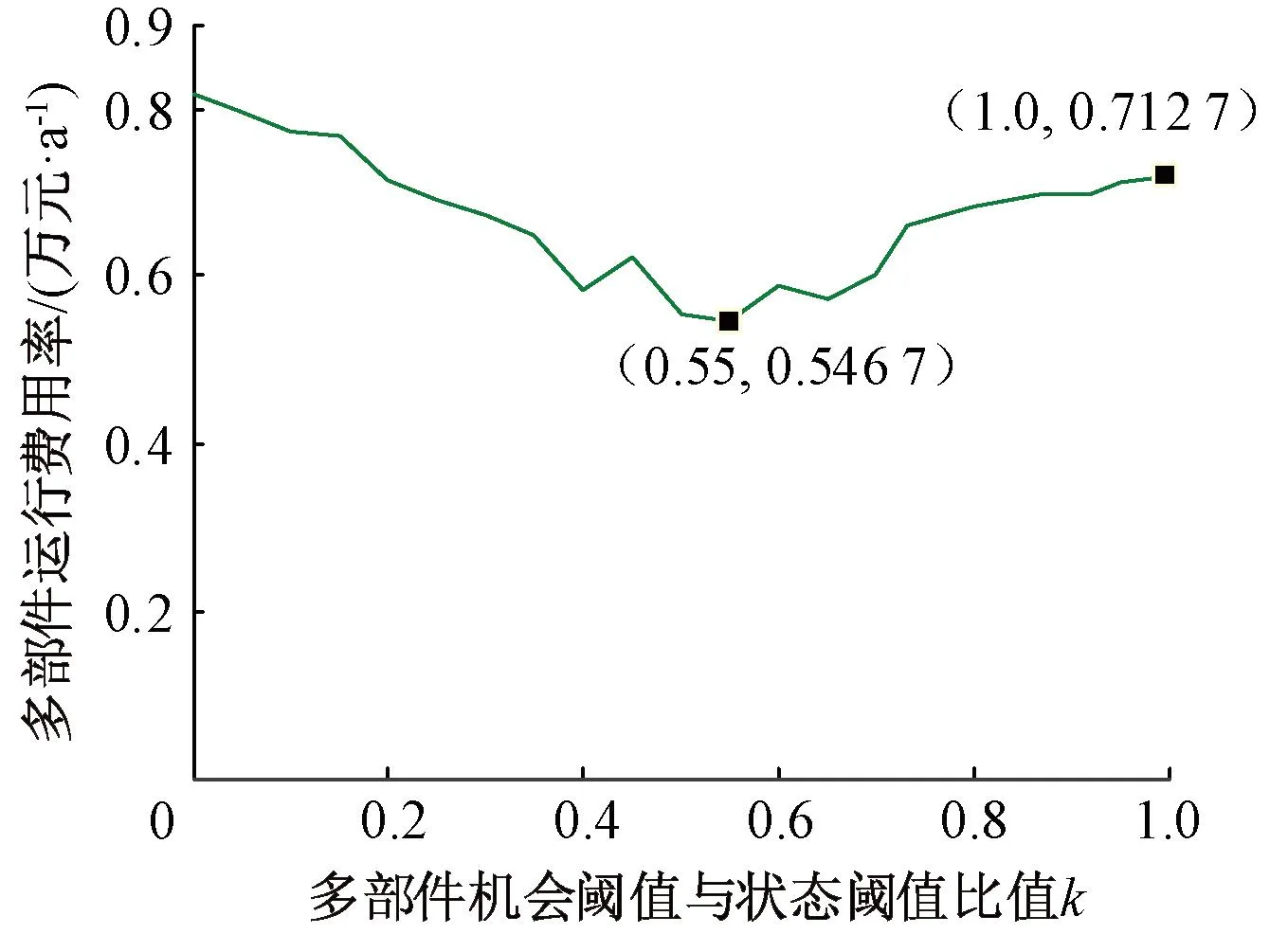
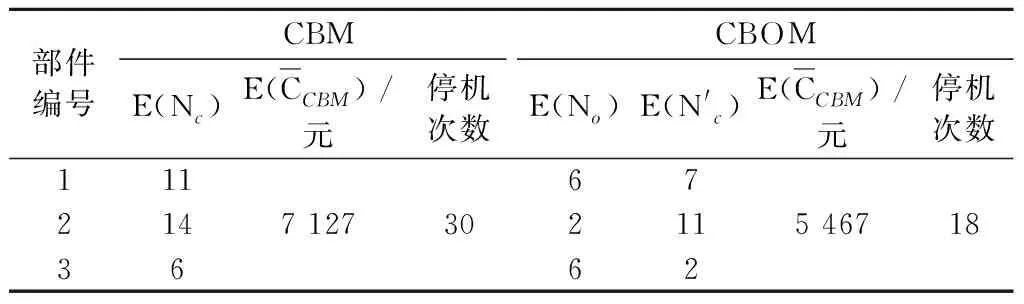
RD(t)=Pr(y(t) (6) 式中:Pr为概率函数;FD为不可靠度;Φ为正态分布函数。 部件在实际预防性维修中,由于受维修人员的水平、维修工具的优劣以及其他部件退化过程的影响,在部件进行预防性维修后,部件的状态一般在“修复如新”和“修复如旧”中间的某一状态,称为部件的不完全维修。如图2所示为动车组部件不完全维修过程示意,yp(h)为预防性维修后部件的退化量,h为预防性维修次数,此时yp(h)≠0,它处于“修复如新”和“修复如旧”的中间某一退化量。对于部件的每个劣化周期,如图2中的[0, t1]、[t1, t2],部件的每个Wiener退化过程是非单调且呈增长趋势的连续函数,区别在于其过程的起始点不同,每个退化过程一定能够从某个状态击中Lo或Lp,因此,对于同一部件而言,在整个生命周期中,该部件的机会阈值Lo和状态阈值Lp保持不变。在不完全维修的情况下,预防性维修的效果随着维修次数h的增加呈下降趋势,因此在部件的一个更新周期内,次数h是有限的[18]。预防性维护后部件的退化量采用基于指数分布的随机几何过程来表示,其期望值为 图2 动车组部件不完全维修过程示意 [1-exp(-εωh-1)] (7) 式中:Lp为部件的预防性维修阈值;ω为部件随机几何过程的比,且ω>1;ε为指数分布参数的常数因子,且0<ε<1,其值根据部件既有历史维修数据,通过最大似然估计法求得。 当部件的退化量超过预防性维修阈值时,将进行不完全的预防性维修,维修后部件的退化量函数yp(t)为 yp(t)=yp(h)+αΛ(t-t0)+βB[Λ(t-t0)] (8) 式中:t0为初始值。 预防性维修后部件的可靠度函数为 RpD(t)=Pr[yp(t) D-yp(h)]=1-FpD(t)= (9) 在保证部件可靠性运行的前提下,以部件的最低运行费用率为优化目标,建立决策模型为 s.t.y(t) (10) 假设部件的所有预防性维修和修复性维修时刻均在检测点进行,且预防性维修为不完全维修,修复性维修为完全维修。部件预防性维修发生的概率包括维修之前未进行过预防性维修和进行过预防性维修两部分。 部件预防性维修发生的概率第一部分为在进行此次预防性维修之前,部件未进行过预防性维护。设部件在第g(g=1,2, …)次检测时,进行预防性维护,此时部件的初始劣化值为0,则部件在gδ时刻进行预防性维修的概率为 P11(g,δ)=Pr(y((g-1)δ) R(gδ,(g-1)δ,Lp-y)]dy (11) 式中:R(t, t1, y)为部件在时间区间[t, t1]内退化增量小于任一退化量y的概率。 部件预防性维修发生的概率第二部分为在本次预防性维修gδ时刻之前,部件已经进行过预防性维护,此时部件的初始劣化值为yp(h),则部件在gδ时刻进行预防性维修的概率为 P12(g,δ)=Pr(yp((g-1)δ) nδ,D-y)-Rp(gδ,(g-1)δ,nδ,Lp-y)]dy (12) 式中:n为在gδ时刻之前的上次预防性维护发生的时刻第n次检测;Rp(t, t1, t0, y)为部件在时间区间[t, t1]内退化增量小于任一退化量y的概率;t0为上次预防性维修发生的时刻。 根据式(11)、式(12),可得部件预防性维修次数的期望值E(N1)为 部件修复性维修次数的期望值E(N2)为 式中:P2(·)为部件修复性维修发生的概率;δs为部件将实时修复性维修的时刻。 根据决策模型(10)可知,以部件的最低运行费用率为优化目标,需要决策两个变量:检测周期δ和预防性维修阈值Lp,通过蒙特卡洛算法求得单个部件最优的组合(δ, Lp),获得单部件的最优决策方案。 因为部件的修复性维护和检测的相关费用在多部件状态维修策略和状态-机会维修策略中同时存在,且不受是否考虑机会维修的影响,因此本节维修策略分析中,仅考虑部件的状态维修、机会维修、固定维修费用以及停机损失。 在不考虑机会维修的情况下,多部件进行状态维修的总费用CCBM期望值可表示为 式中:Cic为部件i实施一次状态维修的成本;E(Nic)为对应状态维修次数的期望值;Cid为部件i的固定维修费用;Cif为部件i的停机损失。 在考虑机会维修的情况下,多部件进行状态-机会维修的总费用期望为 多部件在状态-机会维修策略下的费用率期望值为 (18) 根据图1可知,在时刻gδ,系统中一个部件j的退化量yj(t) ∈[Lp(j), D(j)),另一部件i的退化量yi(t) ∈[Lo(i), Lp(i)),则部件j进行状态维修,部件i进行机会维修。 在时刻gδ,不考虑其他部件是否进行状态维修,部件i进行机会维修的概率为 Pi1(g,δ)=Pr(y((g-1)δ(i)) [R(gδ(i),(g-1)δ(i),Lp(i)-y)-R(gδ(i), (g-1)δ(i),Lo(i)-y)]dy (19) (20) 多部件在状态-机会维修策略下机会维修次数为 在时刻gδ,部件j进行状态维修的概率为 Pj1(g,δ)=Pr(y((g-1)δ(j)) [R(gδ(j),(g-1)δ(j),Lp(j)-y)-R(gδ(j), (g-1)δ(j),Lo(j)-y)]dy (22) Pj2(g,δ)=Pr(yp((g-1)δ(j)) nδ(j),y]·[R(gδ(j),(g-1)δ(j),nδ(j),Lp(j)- y)-R(gδ(j),(g-1)δ(j),nδ(j), Lo(j)-y)]dy (23) 结合式(19)~式(23)可求得部件i在一个设计寿命周期内发生机会维修次数的期望值为 Pj2(g,δ)] (24) 根据图1可知,对于任一部件i有 针对不同的部件,其机会阈值与状态阈值的差值差别较大,为便于计算,采用比值的形式表达机会阈值与状态阈值的关系,即 针对同一系统的多个部件而言,不同部件的退化过程采用不同的状态退化数据,这些数据一般具有不同的量纲。为了便于现场系统的控制检测,不同部件退化量需采用同一个度量尺度,以保证其具有相同的灵敏度,因此,本文假设ki=kj=kq=k,则基于k的部件状态-机会维修决策原理为: Step1根据第2章维修策略确定单部件的最优检测周期δ(i)和状态维修阈值Lp(i),作为初始化参数。 Step2对k进行赋值,0 Step3假设其中一个部件i的退化量yi(t)最先达到其状态维修阈值Lp(i),此时部件i的运行时间为t(i)。 Step4根据时间t(i),判断其他部件j的退化量是否在其机会维修区间[kLp(j),Lp(j)],如在该区间,则对部件j实施机会维修,否则仅对部件i实施状态维修。 Step5确定运行时间t(i)是否超过设计寿命TP,若小于设计寿命TP,则转入Step2继续执行程序,直至所有部件的运行时间均达到设计寿命TP。 最后,计算式(18)的费用率值,通过比较不同的k值对费用率的影响,求出最佳的k值,进而求得最优机会阈值,从而确定多部件的状态-机会维修策略。 本文利用蒙特卡洛算法对多部件状态-机会维修决策模型进行仿真求解。 以某线路动车组牵引供电系统3个关键部件牵引变压器、受电弓和牵引电机的现场运行数据为例,进行算例分析,并对3个部件进行编号依次为部件1、部件2、部件3。利用Wiener过程描述3个部件的退化过程,其对应的退化参数见表1[20-22]。三种部件的设计寿命均按照12 a计算[23-24]。在仿真中选取Λ(t)=t。表2为该线路动车组牵引供电系统3个关键部件的维修参数,参数含义同式(10)。 表1 动车组牵引供电系统关键部件退化参数 表2 动车组牵引供电系统关键部件相关参数 根据第2节维修策略和表1、表2的相关参数,利用蒙特卡洛算法可求得每个部件的最优检测周期和状态阈值。所有部件的检测周期取0.1~1,步长取0.05;部件1状态阈值取0~16,步长取0.5;部件2状态阈值取0~2.5,步长取0.05;部件3状态阈值取0~100,步长取5。因为蒙特卡洛算法存在较大的随机性,为了降低这种随机性对仿真结果的影响,在仿真过程中设置每个循环的仿真次数为1 000次,并求取平均值。根据式(10),求得单个部件最低费用率模型下的最优检测周期和状态阈值,如图3所示。 图3 三部件最优费用率求解结果 根据图3可知,三部件的最优检测周期均为0.25年,最优状态阈值分别为10.5、1.57、65,所有部件随着检测周期和状态阈值的增大,其运行费用率均符合先减小后增大的趋势。原因分析:在检测周期和状态阈值取值均较低时,部件存在维修“过剩”,造成运行费用增大;如果检测周期和状态阈值取值较大,部件存在维修“不足”,致使部件进行修复性维修或故障发生的概率增大,增加运行费用。 表3为该线路动车组牵引供电系统关键部件维修费用参数,参数含义同式(15)、式(17)。 表3 动车组牵引供电系统关键部件维修费用参数 万元·次-1 根据表3三部件维修费用参数,按照状态-机会维修策略原理的步骤,采用蒙特卡洛算法,求解状态-机会维修策略决策模型。仿真按照1 000次的次数进行,求得机会阈值与状态阈值之比k与维修费用率的关系,如图4所示。 图4 k与维修费用率关系曲线 由图4可知,在[0,1]区间里,存在唯一的k值,使多部件的维修费用率达到最低。如果k值取值太小,则机会阈值过小,使部件的状态-机会区域过大,造成部件过度维修,引起维修资源浪费;如果k值取值过大,机会阈值过大,使部件的状态-机会区域变小,引起动车组频繁停机,降低可用性,无法体现状态-机会维修策略的优势。因此,选取合适的机会阈值与状态阈值的比值k,对降低部件的运行维修成本具有重要的经济意义。 表4为同等运行条件下,动车组牵引供电系统3个部件的状态维修策略(CBM)和状态-机会维修策略(CBOM)下的维修费用率和维修次数的对比。从表4可以看出,CBOM策略下总的维修次数和CBM下的基本相同,但状态维修次数有所降低,且CBOM策略下维修费用(5 467元)比CBM下的维修费用(7 127元)降低了23.29%,同时CBOM策略下停机次数比CBM下的减少了12次。 表4 动车组牵引供电系统关键部件维修费用率、维修次数及停机次数对比 本文提出基于随机过程的多部件状态-机会维修优化模型,该模型不仅利用Wiener过程和随机几何过程描述了单部件的不完全维修,并确定单部件的最优状态阈值和检测周期,而且考虑了处于不同状态下多部件的维修,引入机会阈值与状态阈值的比值,建立状态-机会维修策略模型,并利用蒙特卡洛算法对模型进行求解。同时,利用随机过程和拓扑的基本理论,分析状态检测周期的大小与不同检测策略之间的关系,从拓扑的角度,证明状态-机会维修是状态维修的一种优化策略。算例分析表明,机会阈值的合理取值,能够避免各个部件的过维修和欠维修,节约了维修成本,减少了停机次数,提高了部件的可用性,对动车组部件的维修工作提供了一定的参考。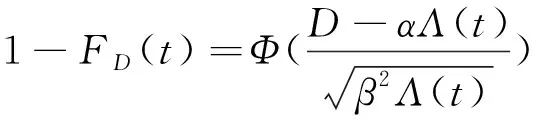
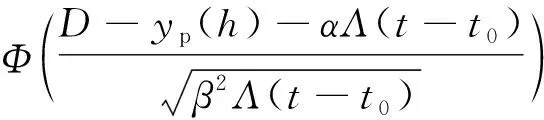
2 单部件状态维修策略及状态阈值的确定

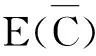
3 多部件机会阈值的确定
3.1 维修费用分析

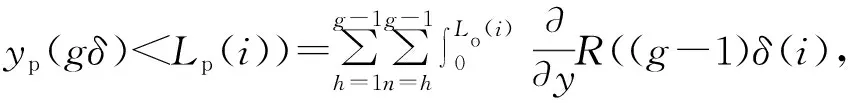
3.2 机会阈值的求取
4 算例分析




5 结论

