不同滑带角度滑坡作用下隧道衬砌与抗滑桩结构非线性受力特征研究
李 涛,罗 波,朱宝龙,陈 刚
(1.中国工程物理研究院 总体工程研究所,四川 绵阳 621999;2.中国五冶集团有限公司,四川 成都 610063;3.西南科技大学 土木工程与建筑学院,四川 绵阳 621010)
为保证建设中公路、铁路线路顺直,在一些特定区域不得不采用隧道穿越大型滑坡的设计方案,或者在工程建设前期勘察工作疏忽导致选线穿越滑坡地带,由此形成特定的隧道-滑坡体系。工程建设中为防止滑坡体影响隧道衬砌结构正常工作,多采用抗滑桩支护方式保证隧道衬砌结构安全[1-2]。
滑坡-隧道体系由于地形复杂、滑坡体纵横变化幅度较大,滑坡隧道相互作用受力变形机理较为复杂,在工程建设中对其治理问题一直是研究热点。当前实际工程研究中主要集中在以下方面:①对滑坡-隧道类型进行划分,吴红刚等[3-5]以隧道轴线与滑坡主滑方向线相交位置关系不同分为正交、斜交、平行,并以这三种体系为核心对滑坡体系受力特征与荷载计算作了较为完备的研究。胡炜等[6]、卢光兆等[7]分析不同埋深隧道,提出隧道拉裂、剪切、岩体自身破坏三种破坏类型。②针对滑坡隧道在不同工况下受力特征进行研究,隋传毅等[8]、毛坚强等[9]研究隧道在不同地震波情况下隧道受力特性,得出在情况一定的条件下隧道对地震波有明显的选择性,并对滑带影响下隧道滑坡相互作用机理进一步研究。Causse等[10]、Li等[11]研究了深埋隧道边坡滑移及平行于隧道的滑坡在蠕变过程对隧道结构的损坏。邵江等[12]对在不同滑带角度下滑坡隧道体系所受偏压状况进行更进一步研究,得出当滑带角度逐渐增大时隧道偏压比会逐渐减小。同时,随着数值模拟技术的进步,越来越多的专家学者[13-17]通过有限元或者离散元法对已有隧道情况下再次隧道开挖时隧道变形机理研究。③针对滑坡隧道体系在治理手段方面的进一步研究,如李涛等[1]对不同桩间距条件下隧道受力特征进行分析,得出正交滑坡隧道体系中最优抗滑桩支护间距。田四明等[18]提出超前支护、预应力锚索等主动改变隧道围岩应力为核心的方法,降低滑坡对隧道体系的损伤。部分学者[19-25]对山区滑坡区域既有隧道在锚索加固、抗滑桩支护手段下滑坡体与隧道之间相互作用机理进行研究,得出隧道沉降、隧道弯矩等明显小于未支护前隧道受力情况。不同支护方式得到的支护效果也有较大差异,抗滑桩对滑坡阻滑效果较为显著,且经济节约。虽然,前人研究成果为部分工程提供了一定参考依据,但是绝大多数都依托于某一特定工程,对于其他工程项目缺乏普遍适用性。目前还缺乏对不同滑带角度作用下,有抗滑桩支护体系的隧道-抗滑桩受力特征研究。
因此,本文利用模型试验结合数值模拟方法[24-27]对6种不同滑带角度(0°、10°、20°、30°、40°、50°)下桩-隧体系受力特征进行研究,得到不同滑带角度作用下支护桩体及隧道衬砌结构随滑带角度变化而变化的非线性受力特征。这对于弥补滑坡隧道体系研究不足,掌握不同滑带角度下桩-隧体系受力特征有一定工程实际意义。
1 模型试验设计
1.1 滑坡隧道工程实例
部分国内滑坡隧道体系破坏案例分析见表1,滑带角度多在0°~50°范围,且多在靠近滑坡侧左拱和拱脚处出现破坏。因此,本文研究6种滑带角度条件下桩-隧体系受力特征,为以后实际工程项目提供相应参考。

表1 不同滑带角度滑坡隧道案例对比
本文以简化南坪隧道为研究原型,在此基础上模拟6种不同滑带变化,其剖面示意见图1。隧道内部破坏较为严重,水沟受到挤压,盖板鼓起,位移量达6 cm,且在隧道内侧出现长达28 m裂缝,见图2。隧道在与滑带相交处发生局部剪切变形,且其基本在山侧发生破坏变形。
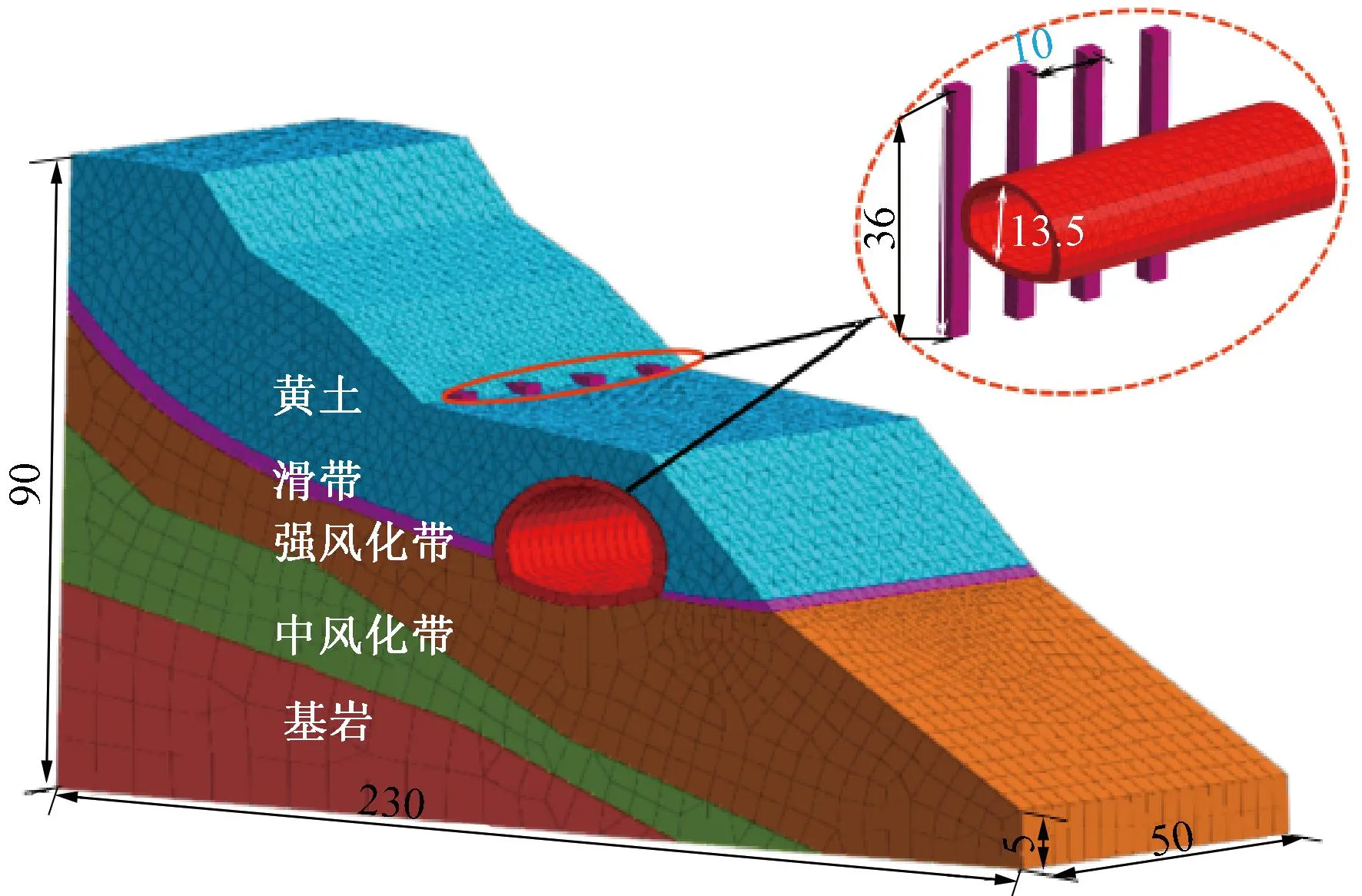
图1 南坪隧道地质原型示意(单位:m)

图2 南坪隧道变形破坏特征
1.2 不同滑带将角度下滑坡隧道室内模型试验设计
1.2.1 模型试验相似比设计
由模型试验相似理论,本文以1∶100设计滑坡-隧道模型试验,弹性模量按1∶1设计,根据几何相似理论可得:Cq=1/100、Cp=1/10 000、Cσ=1/100、Cγ=1、CAc=1/100、CM=1/100 000、Cμ=1等基本材料参数相似比。其中:q为桩身线荷载;p为桩身集中力,σ为桩身应力,γ为重度,Ac为桩截面面积,M为弯矩,μ为泊松比。
1.2.2 桩体参数选择
1)桩长及桩径
根据实际工程选择的土质情况及工程实况,选取抗滑桩模型尺寸,长为3.6m,宽为2.4m,高为36m,并确定水平方向桩数量为4根。
2)桩距
根据大准铁路南坪隧道结构原型,在实际工程确定桩体数量时,当桩体间距过小时虽然能减少坡体滑动趋势,但是桩体无法完全发挥自身承载力。当桩体间距过大时,可能会无法满足坡体抗滑变形要求导致土体滑动同时也容易造成桩顶的应力集中无法正常工作。桩间距设计基于桩体成孔仅侧向挤压及土体挤密仅有孔隙变化这两个基本假设。桩距计算公式为
(1)
式中:S为桩距;d为桩宽;fpk为承载力标准值;fsk为加固前承载力标准值;fspk为处理后承载力标准值。
根据式(1)当d=2.4~3.6m时桩间距取10m,对应抗滑桩布置形式见图3。

图3 抗滑桩布置形式(单位:cm)
1.2.3 模型试验设计与制作
按照1∶100的缩尺,设计模型长宽高分别为230、50、90cm,见图4,整体物理模型见图5。为更好地体现试验效果,模型中滑体采用西南地区本地黏土为主要材料,以每5cm为一层分层填筑,按照工程实际工况滑床压实度设计为96%~98%,滑体压实度设计为90%~93%。选用与实际工程相同含水率18.2%,通过直剪试验测得滑体黏聚力c=30 kPa,内摩擦角φ=23°。滑床采用砾石、碎石、黏土以及少量石灰混合而成,再经过分层重压尽量减少沉降,通过直剪试验测得c=40 kPa,φ=26°。采用双层塑料薄膜内填充滑石粉来模拟主滑带,利用传递系数法反算得出c=16 kPa,φ=7°。
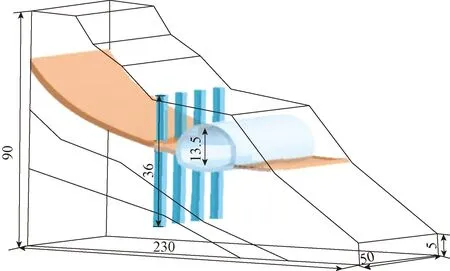
图4 滑坡-隧道模型示意(单位:cm)

图5 滑坡-隧道模型试验实物(单位:cm)
在滑床铺设完成后,按照工程原型位置等比例先埋设抗滑桩体,并深入模型滑床体内12 cm视作锚固段,在抗滑桩施工完毕后再安置隧道。抗滑桩模型高为3.5 cm,宽为2.5 cm,长为36 cm,隧道模型高为13.5 cm,长为50 cm。采用1.0 cm间距的钢丝网编制成主体骨架,再用PVC模具夹合,内部空隙灌注水浆比为1∶2的模型石膏浆液,放置3 d,待完全硬化后脱模,测得材料参数γ=22 kN/m3、E=0.286 GPa、μ=0.22。
试验模型槽中,桩体布置按照工程实例一致,在近山侧隧道长50 cm范围内布置4根抗滑桩,桩间距为10 cm。为消除边界效应,抗滑桩距离模型槽均为10 cm,且模型槽观察侧采用钢化玻璃,另一侧采用木板上覆盖薄膜措施以减少两侧摩擦。
模型试验采用滑带角度0°、10°、20°、30°、40°、50°研究桩-隧体系受力特征。当一组试验完成后,重新调整模型进行下一组试验。
1.2.4 测点布置
为保证试验数据的可靠性,在隧道截面周围分别布置内外24个应变片测点及9个土压力盒测点。在抗滑桩桩身周侧也布置应变片测点,应变片第一测点及最后一个测点分别距离桩顶、桩底2 cm,其他各测点之间相距4 cm,在滑面接触位置加密布置2个测点共12个测点,桩体靠近滑坡侧(桩前)与背离侧(桩后)均相同布置;在桩体前后侧布置应变片空隙处各布置5个土压力盒测点,其中两个为备份参考,见图6。在滑坡体上部、抗滑桩中间桩位以及滑体下部均布设1位移计,测量加载过程中三者水平位移。
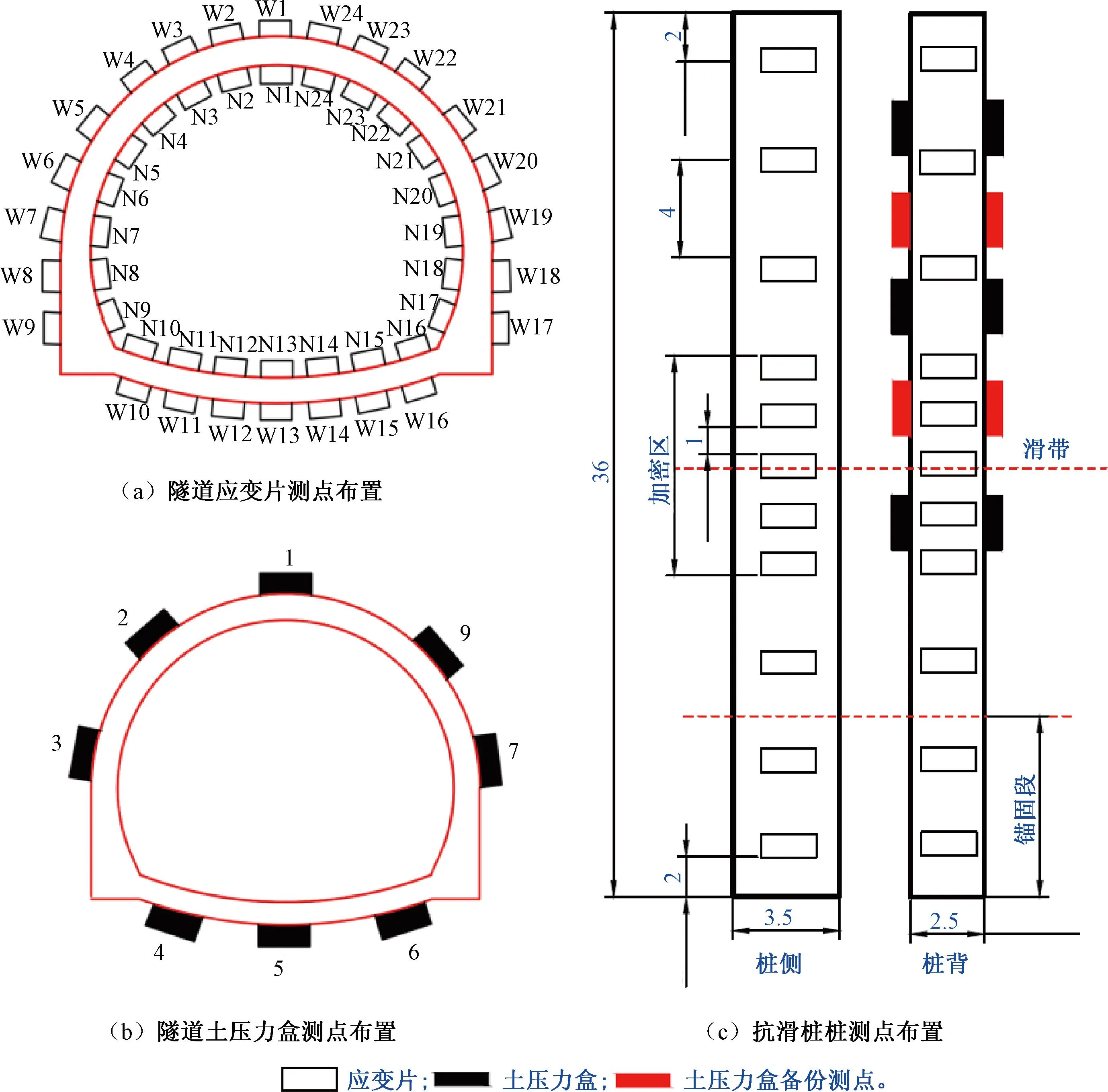
图6 测点布置(单位:cm)
1.2.5 加载方案
试验采用10 t液压千斤顶进行加载[1,3],其加载过程中能最大限度破坏滑坡体,这样可以充分验证抗滑桩对隧道的支护效果,假定滑坡所受推力为矩形分布均布荷载。在滑体与千斤顶之间放置一块能完全抵住滑坡体的矩形钢板,使千斤顶集中荷载转化为矩形均布荷载,由滑体后侧进行加载,具体加载布置见图7。本次试验按滑带滑带角度0°、10°、20°、30°、40°、50°共分为6组,分级加载模式见表2,每次加载步长5 kN。荷载P由0 kN时加载至5 kN加载时间15 min,完成后维持20 min,依此保证滑体与加载装置间完全贴合。后续随着施加荷载逐步增大,加载时间及维持时间也相应增加。最后加载至35 kN时维持荷载直至滑坡模型失效。此时,监测上部滑体位移装置已失效,桩体产生较大位移,且滑体沿着滑带沿着隧道顶部剪出。
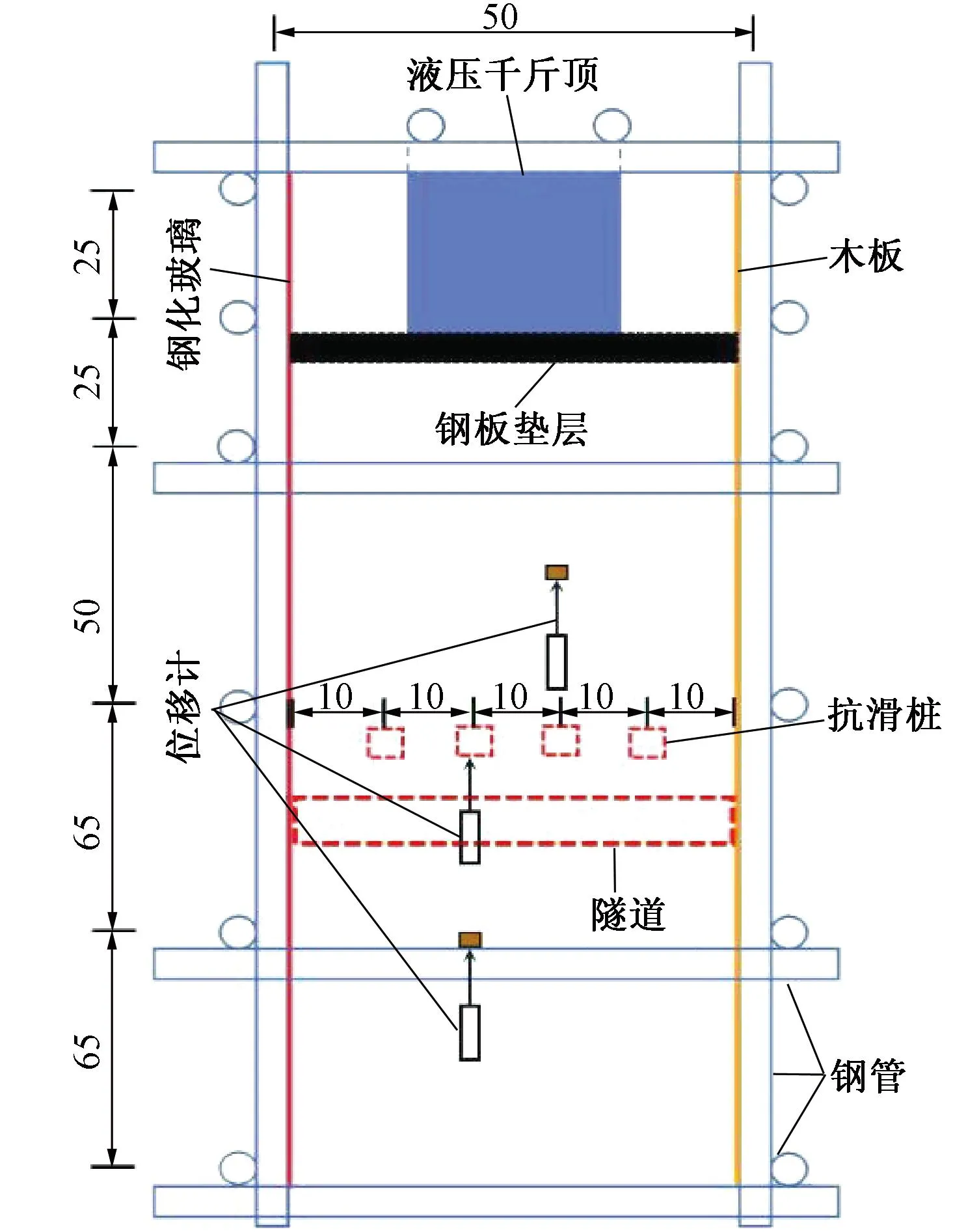
图7 滑坡加载示意(单位:cm)

表2 模型试验加载方案
2 模型试验结果与分析
2.1 模型试验破坏特征
模型破坏示意见图8,加载前见图8(a),桩体间距10 cm,坡体与桩顶处各有一位移计。预加荷载时(0~5 kN),滑带角度为0°、10°、20°、30°、40°、50°时隧道与桩体模型均无明显变化。随着荷载逐步增大,桩顶后侧与滑体逐渐分离,滑体上部出现细微裂缝,见图8(b)。滑带角度为0°、10°、20°、30°、40°、50°时滑体所产生第一条贯穿横裂缝,所加荷载分别为15、17、18、21、23、26 kN。滑带角度为0°、10°、20°、30°时在荷载值为23、27、29、32 kN时桩体与上部滑体分离形成如图8(b)所示的脱空区[27]。而滑带角度为40°、50°时未出现脱空现象。在滑带角度为0°、10°、20°、30°并桩体与滑体之间形成脱空区时,下部隧道也出现微小位移。当加载结束,即P=35 kN,滑带角度为0°、10°、20°、30°时桩体与滑体之间形成脱空区宽度分别为6、4、2、1 cm,深度分别为15、11、8、4 cm。综上可知对于6种不同滑带角度作用下,桩体与上部滑体出现大小不一的横向裂缝及脱空区。随着滑带角度的逐渐增加,裂缝大小及脱空区深度和宽度逐渐减小,当滑带角度为40°、50°时,桩体后侧与滑体几乎不会出现脱空现象。
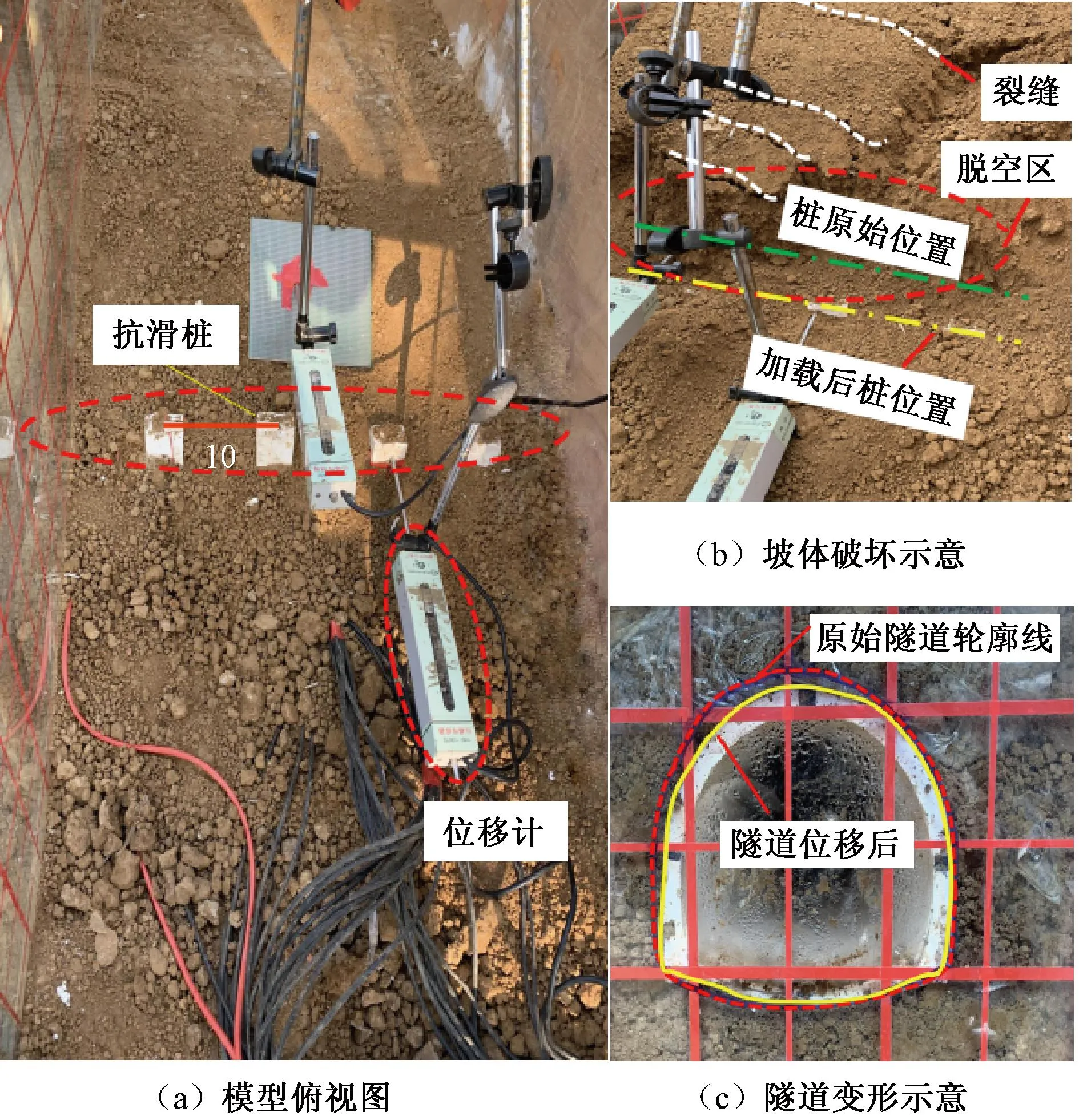
图8 模型破坏示意(10°滑带)(单位:cm)
随着荷载增大,6种不同滑带角度作用下隧道上部覆盖土体也逐渐出现不同程度裂缝,并且逐渐加宽变深。当加载结束后,滑带角度为0°、10°、20°时隧道处滑坡土体变化最明显。上部土体沿着滑带处由隧道顶部剪出破坏,如图8(c)所示,隧道分别出现5、3、1 mm位移。表明,不同滑带角度对隧道剪出破坏程度不一致,由大至小所对应滑带角度为0°、10°、20°、30°、40°、50°。
通过观察侧发现,6种不同滑带角度作用下抗滑桩在滑面附近仅出现微微前倾现象,并未产生较大变形破坏。但滑带角度不同,抗滑桩桩身前倾程度也不相同,由大至小所对应滑带角度为0°、10°、20°、30°、40°、50°。表明,滑带角度越大桩体所分配滑坡推力越小。
2.2 位移分布规律对比分析
在6种不同滑带角度的滑坡作用下模型坡体位移与桩顶水平位移随时间的变化曲线见图9、图10。由图9、图10可知:
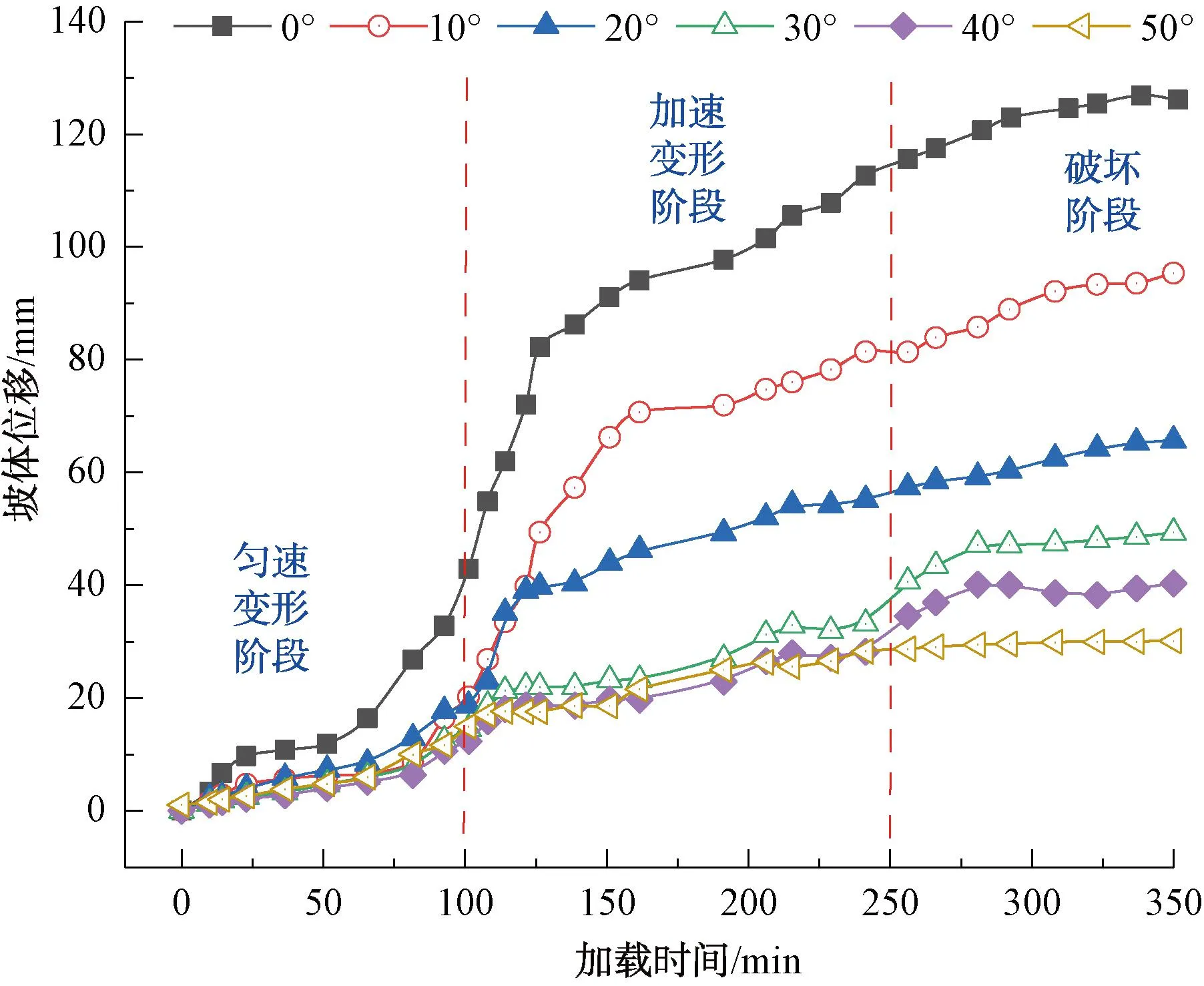
图9 不同滑带角度下坡体位移
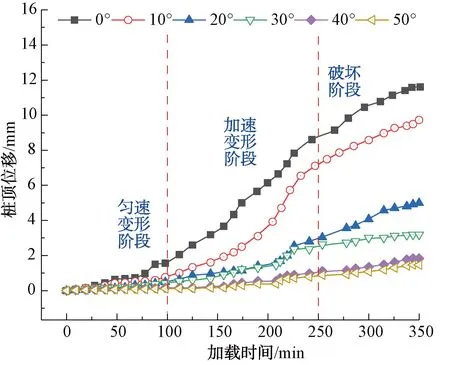
图10 不同滑带角度下桩顶位移
1)6种不同滑带角度对应的桩顶位移及滑坡体位移由大至小所对应的滑带角度为0°、10°、20°、30°、40°、50°。
2)在滑带角度为0°、10°、20°时,坡体位移以及抗滑桩桩顶水平位移明显大于滑带角度为40°、50°时。结束加载后不同滑带角度作用下坡体最大水平位移为128 mm,出现在滑带角度为0°,最小水平位移为30 mm,出现在滑带角度为50°,降幅约为76.5%。同时,桩顶位移与滑坡体位移呈现相似趋势,在滑带角度为0°时出现最大位移值为11.9 mm,50°时出现最小位移值为2.0 mm,降幅约为83.1%。
3)滑带角度为0°、10°、20°时,滑坡体水平位移及桩顶水平位移随着加载时间的增加而出现急剧增长趋势;在加载时间0~100 min(对应荷载0~15 kN)时,这3种滑带角度的位移整体趋势呈现平缓增加趋势,在100~250 min(对应荷载15~30 kN)时,滑坡位移速率增快,坡体出现较深纵向裂缝。在250~350 min(对应荷载30~35 kN),此时坡体变形速率降低已出现破坏现象。对应加载过程中坡体的发展变化,将滑坡破坏演化分为匀速、加速、破坏变形三个阶段,此时隧道桩体也呈现相似变化,见图9、图10。
4)在荷载不断增加过程中隧道结构也产生了一定位移,当滑带角度为0°时产生5 mm左右位移,当滑带角度为40°、50°时隧道相对于原始位置几乎未产生位移。可知当滑带角度逐渐加大的过程中,隧道衬砌结构变形逐渐减少。
5)在滑带角度为0°、10°、20°、30°、40°、50°时,桩顶水平位移的变化幅度较大,表明滑坡角度的改变对抗滑桩的受力影响较大,对抗滑桩所保护的隧道也有较大的影响,因此研究不同滑带角度下抗滑桩与隧道衬砌结构非线性受力特征为实际工程滑坡治理有较大的借鉴意义。
综上,当滑带角度为0°、10°、20°时,其对坡体水平位移和桩顶、隧道位移影响远大于滑带角度为30°、40°、50°时。这表明在进行隧道-滑坡体系治理时应当依照其实际勘察所得滑带角度制定合适方案。
2.3 土压力分布特征
在试验中测得桩体前后侧及隧道衬砌结构土压力为
P=Kε
(1)
式中:P为土压力;K为土压力盒率定系数;ε为测得土压力盒应变。
图11、图12为施加荷载为35kN时6种不同滑带角度作用下,抗滑桩体及隧道受力体系所受土压力分布示意。可以看出不同滑带角度作用下桩体在滑面附近土压力均趋近于0。且随着滑带角度的增大,桩体土压力由302.9kPa减小至78.3kPa(减少约74%),隧道左侧拱土压力由83.4 kPa减小至20.3 kPa(减少约75.5%),抗滑桩体及隧道受力体系均同步减少。由于隧道与桩体形成同一受力体系,桩前滑体滑移受到二者共同限制,导致桩顶自由端受到二者共同挤压,出现滑面上部与隧道相互作用区域桩体土压力增大现象,桩前滑体抗力呈倒三角形分布。同时,当滑带角度大于30°时,隧道拱脚处与底拱处土压力分担量逐步加大,左侧隧道衬砌与拱脚处土压力承担比值趋近于1。这表明,随着滑带角度加大,滑坡体荷载形式由水平荷载分布逐步演化成以竖向荷载分布为主。实际工程中当滑带角度大于30°应当注意隧道衬砌结构竖向支护。

图11 不同滑带角度下抗滑桩在不同荷载下的土压力分布(单位:Pa)
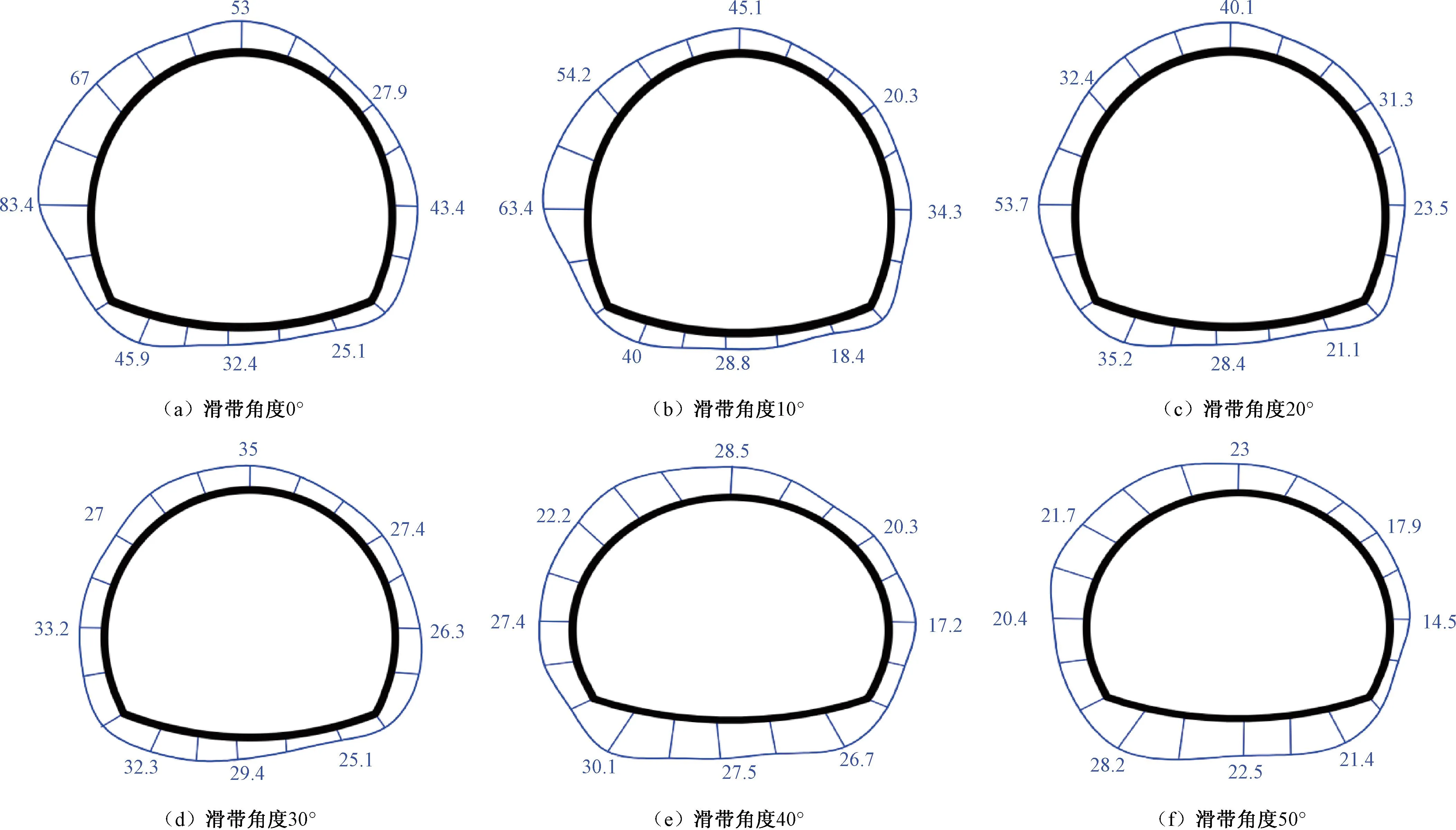
图12 不同滑带角度下隧道在不同荷载下的土压力分布(单位:Pa)
2.4 桩身与隧道弯矩分布规律分析
试验中将桩体前后侧,隧道内外两侧均粘贴应变片,由弯曲理论可知,隧道弯矩Mt为抗滑桩弯矩为

(2)
式中:r隧道内径;R隧道外径;E为隧道衬砌弹性模量;ξ为应变片测量值。
抗滑桩弯矩为
Mp=EI(ε1-ε2)/2h
(3)
式中:Mp为测点处的截面弯矩;EI为桩的抗弯刚度;ε1、ε2分别为测点桩前桩后应变;h为抗滑桩截面高度。
利用最小二乘法对弯矩计算数据进行二次深度拟合,得到弯矩函数[31]为
(4)
式中:a0、a1、…、an分为拟合待定系数。
经过试算,对各种不同滑带角度桩体弯矩采用双参拟合(n=2)可得最优解,即
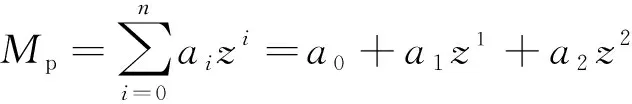
(5)
图13、图14为拟合后桩体与隧道弯矩分布。

图13 不同滑带角度抗滑桩在不同荷载下的弯矩分布
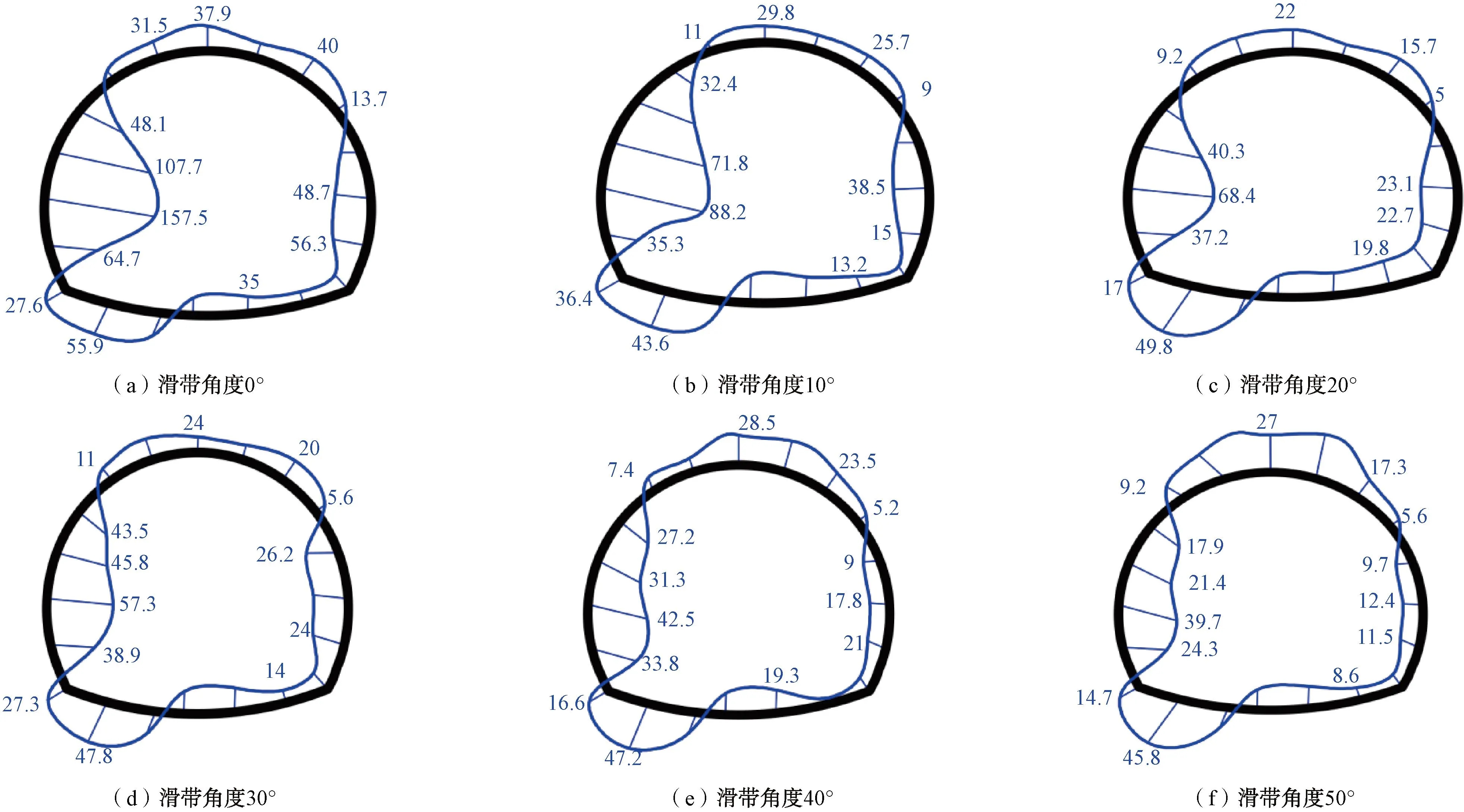
图14 不同滑带角度隧道衬砌结构在不同荷载下的弯矩分布(单位:N·m)
图13、图14表明,在6种不同滑带角度作用下桩身弯矩与隧道衬砌结构弯矩分布规律趋于一致(隧道弯矩以受压为负,受拉为正,即内侧弯矩为负,外侧为正):①桩身弯矩值分布均呈现出S形非线性受力特征,在滑面附近均出现弯矩值为0的交点,且在不同等级荷载作用下反弯点均出现在桩身20~22cm范围;②隧道随着滑带角度逐渐增大,在靠近滑体侧拱弯矩值均逐渐减小,而靠近滑体侧拱脚处弯矩分布占比却逐渐加大;③桩体在滑面上部(抗滑段)所受弯矩绝对值大于滑面下部弯矩绝对值,隧道靠近桩体侧侧拱弯矩也大于远离侧弯矩值;④在滑面上侧及隧道两侧均出现弯矩负值,表明在抗滑段均承受拉应力;⑤不同滑带的作用下,加载过程中,桩-隧体系所受弯矩呈现出非线性变化,桩体弯矩主要集中在滑面以上抗滑段,隧道主要出现在靠近桩体一侧的隧道拱侧处。上述现象表明,不同滑带角度作用下抗滑桩体与隧道之间形成同一受力体系,两者间协同作用、变形协调。
不同滑带角度作用下的区别在于:①最大弯矩值由大至小所对应滑带角度分别为0°、10°、20°、30°、40°、50°;滑带角度由0°增大至20°时,抗滑桩与隧道弯矩值均产生了大幅降低,降幅约为37.9%(滑带角度变化0°~20°),但是弯矩变化值降低幅度明显小于滑带角度由30°增大至50°时的变化,降幅约为66.5%。这表明,滑带角度由0°增大至20°时抗滑桩体与隧道受力体系所承受荷载远大于滑带角度由30°增大至50°时所承受荷载。②滑带角度为0°、10°、20°、30°时,桩身受荷P≤15 kN时,弯矩值增长呈现出匀速且缓慢的增长趋势。当15 kN≤P≤25 kN时桩身弯矩值呈现出急剧增大趋势,当P≥25 kN时,弯矩增长率显著降低,与2.2节坡体破坏三阶段(匀速、加速、破坏)宏观相似,证明所得到的模型破坏形态与结构内力变化吻合。而滑带角度为40°、50°时桩体弯矩变化并未出现此现象,与上述观察到的“滑带角度40°、50°时,桩体后侧与滑体几乎不会出现脱空现象”相吻合,在P≥30 kN时桩体弯矩值依旧在缓慢增长。③当滑带角度0°、10°、20°、30°时,隧道近桩侧拱脚处弯矩与隧道最大弯矩比值均小于1,而滑带角度为40°、50°时拱脚处弯矩与隧道最大弯矩比值大于1。表明在滑带角度为40°、50°时,隧道受力更多的是来源于上部荷载压力而非是水平滑体的推力,且随着滑带角度增加,水平滑坡所施加的水平推力逐渐减小。
综上所述,滑带角度在0°、10°、20°、30°时,桩体与隧道结构所受到的滑坡水平推力远大于滑带角度为40°、50°时。滑带角度增加到40°、50°时,水平滑坡推力对隧道结构的影响将小于滑坡竖向荷载对隧道的作用。此时,抗滑对隧道支护效果衰减较为显著。
由模型试验破坏特征、位移分布规律与桩体隧道受力特征分析表明,当滑带角度逐渐增大(由0°至50°)时,抗滑桩体与隧道所受水平推力逐渐减少,隧道衬砌结构在拱脚处所受荷载相较衬砌整体受力比重加大。在滑带角度为0°、10°、20°、30°时,滑坡水平推力对隧道衬砌结构受力影响较大,在滑带角度为40°、50°时滑坡水平推力影响显著衰减。因此,在隧道-滑坡体系中设计抗滑桩支护时,应当考虑实际工程中滑带角度值进行设计。当滑带角度大于40°时,可采用小直径或大桩距的抗滑桩体进行支护;同时,对隧道竖向衬砌结构应考虑支护,对拱脚部位加固。当滑带角度小于30°,应仔细尽量选择大直径桩体或小间距抗滑桩。
3 数值模拟结果分析
3.1 模型参数选择建立
以南坪隧道为原型,采用有限元手段模拟滑带变化对桩-隧体系结构受力特征影响,数值模拟中所用模型参数见表3。分别采用6种滑带角度条件进行模拟分析,分析模型见图15。
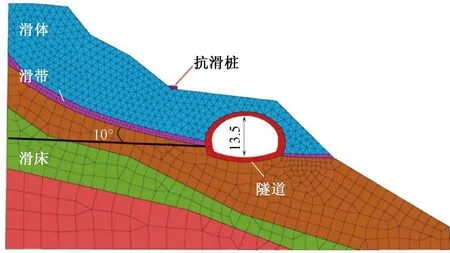
图15 滑带与隧道不同角度数值模拟模型(单位:m)

表3 模型试验材料力学参数
模拟中设置了桩与土、隧道结构与土之间的接触单元,材料参数中桩接触单位极限剪切力为0.99 N/m,法向刚度系数为0.99 kN;桩土以及隧道接触单元主应力刚度模量为2.45 MPa,剪切刚度模量为0.245 MPa,摩擦角为36°。
3.2 不同滑带角度滑坡作用下桩体隧道受力分析
当滑带角度为10°时,桩体及隧道衬砌结构变形位移云图(其他滑带角度下规律相似)见图16。当滑带角度为0°时,桩顶水平位移最大约为1 248.3 mm,隧道变形约为73.7 mm,滑带角度为10°时,桩顶水平位移约为835.4 mm,隧道变形约为53.8 mm,当滑带角度为50°时,桩顶水平位移最大约为156 mm,隧道变形约为6.7 mm。桩体最大变形位置出现在滑面上部自由端,隧道最大变形位置出现在靠近山体侧左拱。可以看出最大变形位置均发生在隧道靠山侧与抗滑桩顶端处,同时,随着滑带角度的增大,隧道衬砌结构变形逐渐减小,这与模型试验得出的位移规律相吻合,仅在变形量数值上略有差别。并且隧道衬砌结构最不利位置由于有抗滑桩保护基本不会产生较大位移变形。

图16 数值模拟滑带角度10°时桩身、隧道位移变形云图(单位:m)
数值模拟所得不同桩间距下桩体与隧道衬砌结构所受弯矩作用见图17、图18。与模型试验所得规律基本一致,桩身最大弯矩出现在滑面上方部位,反弯点出现在滑面位置,整体弯矩呈现出S形分布。隧道最大弯矩值分布在靠山侧的拱脚处,整体弯矩依旧呈现出隧道两侧侧拱受压出现负弯矩值,仰拱与拱脚受拉出现弯矩正值。滑带角度为0°时桩身与隧道所受弯矩最大分别为44 921、17 597 kN·m。滑带角度为50°时桩身与隧道所受弯矩最大分别为11 182、4 928 kN·m。与模型试验规律相吻合,随着滑带角度的增大,桩体与隧道衬砌受力结构所受弯矩逐渐减小。

图17 数值模拟桩身弯矩示意
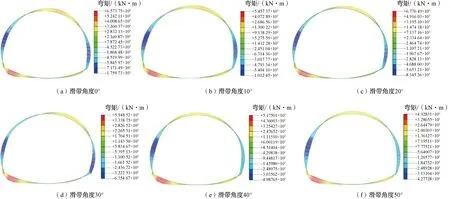
图18 数值模拟隧道衬砌弯矩示意
综上所述,利用数值模拟对不同滑带角度情况下桩体与隧道衬砌结构受力变形进行分析,结果可以看出,当滑带角度逐渐加大(由0°增加至50°)的过程当中,隧道与桩体整体受力变形在逐渐减少,并且在不同滑带角度作用下桩体对于隧道衬砌防护效果有较大差距,当滑带角度增大至40°~50°时,隧道衬砌结构主要受力由左侧拱转移至拱顶与拱脚处,桩体受力最大值点也稍有上移。滑带角度由0°增加至50°时,桩体受力降低约75.1%,隧道衬砌受力降低约72%,两者下降比例相近。在此过程中,隧道拱脚受力与左侧拱受力比却逐渐由37%增加至115%,表明随着滑带角度增加,隧道受力方式逐渐由水平向荷载转变为竖向荷载,与模型试验所得结论“当滑带角度增加到40°、50°时水平滑坡推力对隧道结构的影响将小于滑坡竖向荷载对隧道的作用”吻合。
3.3 数值模拟与模型试验桩体隧道弯矩对比
数值模拟是按照工程断面实际尺寸进行的稳定性以及受力模拟,室内模型试验由于条件限制进行的是1∶100缩尺试验,因此在数值模拟与模型试验桩体以及隧道弯矩对比时,将实际数值模拟按照测点布置将所得弯矩值导出缩小1/100 000进行处理,结果见图19、图20。
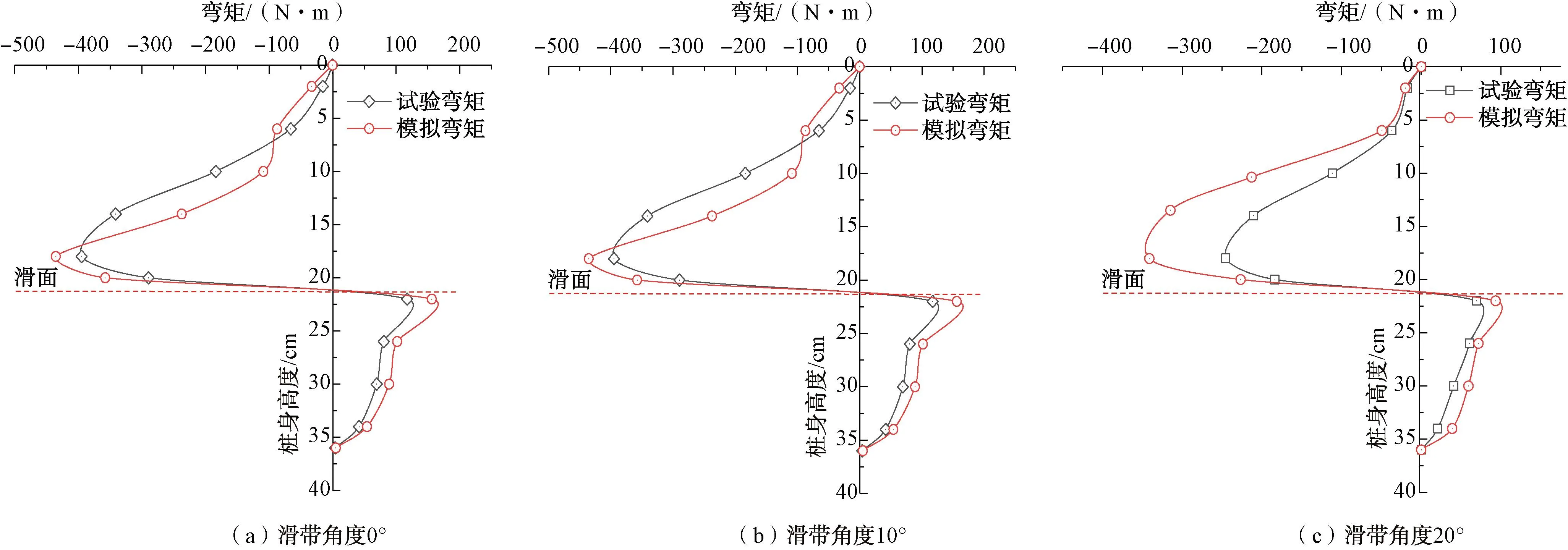
图19 桩体数值模拟与模型试验弯矩对比
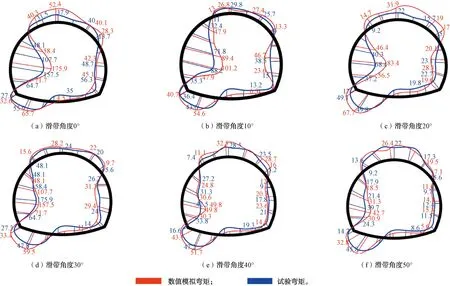
图20 隧道数值模拟与模型试验弯矩对比(单位:N·m)
由图19、图20可知,整体桩体与隧道受力趋势基本保持一致,随着滑带角度增大桩身与隧道结构所承受弯矩值也逐渐降低。在数值模拟所得结果相比较模型试验值普遍较大,其主要原因是在数值模拟中可以达到理想的极限破坏状态而室内试验由于条件限制较难完成。
综上,可以看出在无论是通过手段还是试验方法对于不同桩间距情况下隧道衬砌结构受力变形分析,都可以得出一致的结论,当滑带角度增大(由0°增加至50°)的过程当中,隧道与桩体整体受力变形也在逐渐降低,也可看出隧道拱脚处受力占比逐渐增大。这表明,无论是模型试验抑或者数值模拟所得结果均一致。
4 结论
以大准铁路南坪隧道为例,利用室内模型试验与数值模拟手段相结合的方式,对不同滑带角度作用下桩体与隧道衬砌受力体系非线性受力特征进行相关研究,得到如下结论:
1)加载过程中随着滑带角度增加,桩体与滑坡体之间形成的脱空区(由滑带0°时的6 cm降低至50°时0 cm)逐渐减少,桩身与隧道结构受力逐渐降低。
2)在同荷载下,桩-隧结构位移、土压力、弯矩均随着滑带角度增大而减小,由0°增大至50°时桩身弯矩降低约66·6%左右,隧道弯矩降低74%左右。且滑带角度由30°增大至50°时的降低约42%,滑带角度由0°增大至20°时弯矩降低约22%,滑带角度由30°增大至50°时的降低幅度约为滑带角度由0°增大至20°时弯矩降低幅度的2倍。
3)通过试验分析与数值模拟对比发现:随着滑带角度增大,抗滑桩体与隧道所受水平推力逐渐减少,隧道衬砌结构拱脚、拱顶处所受竖向荷载比值加大。在滑带角度为0°、10°、20°、30°时,隧道侧拱所受水平最大推力与隧道拱顶所受竖向荷载比值由4.15降低至2.38,在滑带角度为40°、50°时该比值降低至1.4左右。可看出在滑带角度小于30°,滑坡水平推力对隧道衬砌结构影响较大,在滑带角度为40°、50°滑坡水平推力影响显著衰减,竖向荷载占比加大。
4)在隧道-滑坡体系设计支护时,为了实际工程经济利益考虑,若遇到的滑带角度小于30°,应当主要考虑滑坡水平推力对隧道结构的影响,可设置直径较大或桩间距较小的抗滑桩对隧道衬砌结构进行保护。当滑带角度大于30°时,应当主要考虑由滑坡体所产生的竖向荷载对隧道衬砌结构的影响,此时应当对隧道仰拱及靠近坡体处拱脚位置重点加固,选用抗滑桩时可采用小直径或大间距以此来提升工程经济效益。

