构网型储能与调相机的暂态过电压抑制能力对比研究

张 兴，李 旭，田 杰，王建安，丁 勇，卢 宇

（南京南瑞继保电气有限公司，南京 211102）

0 引言

高压直流输电系统的送端换流站多建在光伏、风电等新能源大规模开发的偏远地区，电网短路容量低，网架结构较为薄弱，其周边新能源电站包含大量电力电子变换器，自身惯量支撑能力不足。当直流系统出现闭锁、换相失败等故障时，会对送端近区的交流侧电压产生强扰动，导致新能源电站大规模脱网，加剧连锁故障风险［1-3］。

为了改善交流侧电网的暂态过电压问题，需要在送端系统交流侧配置足够的无功储备，一种解决方案是在新能源汇集站配置分布式调相机［4-8］。针对该方案，当前研究主要集中在分布式调相机的配置方法以及参数优化上，如文献［9-10］通过不同的计算方法，提出了分布式调相机的优化配置策略；文献［11-12］则通过建立无功评价指标寻求关键励磁参数及优化规律。目前，青海、新疆等地区正在探索“新能源+储能+分布式调相机”的混合型结构，但该方案对新能源电站配套储能的无功能力未加以充分利用。

GFM（构网）技术是近年来增强区域电网支撑能力的另一种新兴技术。基于GFM技术实现的储能系统整体呈现电压源特性，具备惯量支撑、调频调压、增加短路容量等常规机组具备的主要功能，在构建新型电力系统方面具有广泛的应用前景［13-16］。因此，采用构网型储能替代“常规储能+分布式调相机”的方案亦是一种解决思路。目前，关于GFM技术的电网故障支撑能力研究主要集中在控制方法和稳定性分析等方面，如文献［17］分析了跟网型和构网型变流器控制环路间动态交互作用的区别与同步稳定性机理，文献［18］研究了跟网型和构网型变流器在电力系统振荡机理方面的区别，文献［19］利用等效网络模型对构网型变流器和同步调相机进行了一系列电网振荡下的外特性测试。关于GFM技术在电网异常时支撑能力的分析较少，也尚未有文献针对构网型储能与调相机在直流系统发生故障时的无功支撑效果进行对比。

在现有的构网控制策略中，OPC（开环控制）策略省去了内环，直接将内电势的幅值信号和相位信号合成为调制波［20］，因而更加贴近传统同步机的响应特性。为此，本文基于GFM-OPC 策略进行研究。首先，对其无功控制部分进行建模，对影响无功支撑能力的关键参数进行分析；然后，将其与调相机的励磁控制模型进行统一，并就两者的最大无功输出能力进行对比；最后基于RTDS（实时数字仿真）系统搭建了由青豫特高压直流系统-光伏-调相机-构网型储能组成的试验平台，测试了不同参数下构网型储能在换相失败故障下的故障响应特性，验证了构网型储能在无功响应速度和抑制交流暂态过电压能力方面的效果。

1 构网型储能的无功控制原理

图1 为本文所研究的构网型储能的系统结构。其中，Edc为储能电池单元；Cdc为直流母线支撑电容；L、C、R分别为交流侧滤波电感、滤波电容和等效阻抗；ea、eb、ec为桥臂输出电压；uoa、uob、uoc为经滤波后的变流器端口输出电压；ioa、iob、ioc为交流滤波电感电流；Lg为电网电抗；uga、ugb、ugc为电网三相电压；PCC（公共连接点）为变流器并网点。构网型储能属于功率型储能，其无功支撑能力本身并不过多依赖电池，因此在建模中暂不考虑电池充放电速率对无功支撑能力和响应速度的影响。

图1 构网型储能系统结构Fig.1 Structure of GFM energy storage system

1.1 控制策略

根据GFM理论，简化的转子运动方程可以表示为：

式中：Pref为有功功率指令；Po为实际的有功功率值；J为转动惯量；Dp为有功-频率下垂系数；ω0为电网角速度；ω为GFM 角速度；θ为内电势的电角度。

GFM算法按照下垂公式模拟调压功能，生成端口电压参考值，其dq坐标系下的参考值ud*、uq*如式（2）所示：

式中：Qref为无功功率指令；Qo为实际的无功功率值；Dq为无功-电压下垂系数；Uo为PCC 点的额定电压。

GFM-OPC策略通过式（1）计算出内电势的电角度θ，通过式（2）计算出内电势参考值的幅值，经叠加虚拟阻抗分量后，将该电角度和幅值合成为最终的内电势，最后通过调制算法得到各开关管的控制信号。

1.2 影响无功支撑能力的参数

根据式（2）可以得到GFM-OPC策略下无功控制环的小信号模型，如图2所示。

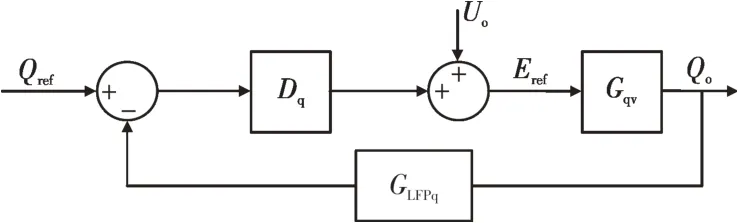
图2 GFM-OPC的无功控制环小信号模型Fig.2 Small signal model of reactive power control loop for GFM-OPC

其中，Eref为内电势的参考值幅值，Gqv为Eref到Qo的传递函数，如式（3）所示：

式中：X为线路阻抗；δ0为当前GFM 工作点的功角；s为拉普拉斯变换参数。

通常，为了增强无功电压控制环稳态下的调节精度和稳定性，对反馈值Qo引入一个低通滤波器GLFPq，如式（4）所示：

式中：ωq为GLFPq的截止频率。

由上文可知，影响GFM-OPC 故障电压暂态支撑效果的参数主要有两个：无功-电压下垂系数Dq和截止频率ωq。

1）Dq的影响

由式（2）可知，端口电压参考值ud*与无功功率Qo呈下垂关系，ud*的大小与Dq成正比。对于GFM-OPC 而言，在电压跌落瞬间，变流器的瞬时无功增大。当Dq大于0时，会导致Eref跟随机端电压下降，这将减弱变流器的瞬时无功出力。

2）ωq的影响

由图2 可以得到反馈环节加入低通滤波器GLFPq后，GFM-OPC的无功控制开环传递函数为：

GLFPq引入会造成无功控制环路的截止频率下降。图3给出了ωq分别为1.6 Hz、106 Hz和318 Hz时TRPC_OPC的幅频特性曲线。可见引入GLFPq后，无功控制环的截止频率向左移动，这将导致无功控制环的响应变慢。

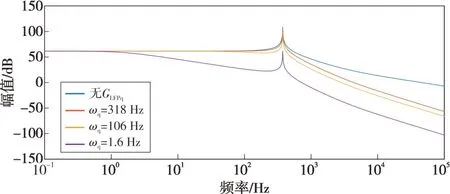
图3 TRPC_OPC的幅频特性曲线Fig.3 Amplitude-frequency characteristic curve of TRPC_OPC

2 构网型储能与调相机无功控制部分的理论对比

从上述分析可知，构网型储能的动态无功补偿效果受相关参数影响。由于其无功控制环节模拟了调相机的响应特性，因此有必要对调相机的无功响应特性进行分析。

当调相机的机端电压出现瞬变时，其无功功率的响应可分成两个部分：一是调相机的次暂态响应，该部分无功功率基于调相机的物理特性，在端口电压发生变化的瞬间自发产生，并随着时间而衰减。二是调相机的暂态响应，该部分基于调相机励磁调节系统，由励磁调节系统通过调整励磁电压而产生，其响应时间一般在数百毫秒。

因此，相比于电力电子无功补偿设备，调相机的无功响应特性区别如下：

1）在数十毫秒的时间尺度内，电压、无功响应主要依靠机组的自身次暂态特性，励磁调节系统的作用很小。

2）励磁调节系统控制响应时间最快需要数百毫秒。

在数十毫秒的时间尺度内，励磁调节系统的响应可以忽略，但是由于构网型储能控制中的无功控制环节模拟的是励磁调节器，因此对励磁调节系统控制模型研究有助于理解和优化构网控制模型。

2.1 构网型储能无功控制与调相机励磁控制的对比

调相机的励磁调节需要同时实现无功与电压的协调控制。稳态情况下以无功功率为控制目标，满足电网当前的无功需求；暂态情况下以电压为控制目标，若发生电压瞬间波动，通过快速强励来稳定机端电压。通常采用无功-电压复合控制策略［21］，其励磁控制系统的控制框图如图4所示。该策略构建电压内环-无功外环的双环控制器，通过引入系统电压参考值Ug来调节系统电压，同时引入无功实际值进行比例调节，提高系统稳态无功输出能力。

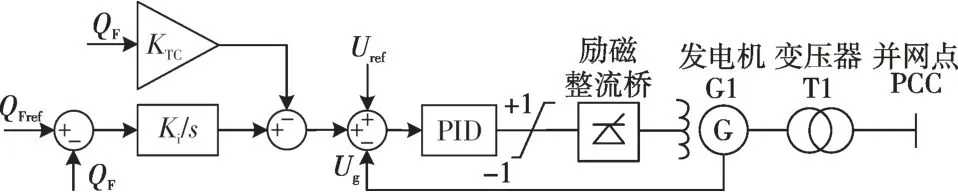
图4 调相机励磁控制系统的控制框图Fig.4 Control block diagram of the excitation control system of synchronous condenser

图4 中，KTC为无功调差系数；Ki为无功外环积分参数；QFref为无功功率指令；QF为调相机输出的无功功率，此处以输出容性无功为正；Uref为参考电压；Ug为机端电压。励磁控制系统的外环是无功功率环，速度较慢；内环是机端电压环，调节速度较快，一般采用串联PID（比例-积分-微分）控制方式进行补偿。其特点在于：

1）调相机正常运行时，通过改变无功功率指令来改变无功的出力。该控制方式可以在不改变暂态电压支撑能力的同时，保持调相机相对稳定的无功功率输出能力。

2）机端电压出现波动时，调相机的机端电压反馈经内环PID 调节器计算后，作用在控制脉冲信号上，同时引入无功实际值进行比例调节，加强机端电压的调节能力。因此当机端电压出现波动时，PID 调节器可以快速响应，保证调相机对电网电压的暂态支撑。

对于无功调差系数KTC而言，在一定程度上其取值越大，下垂特性越显著，并联越稳定，但电压特性越软，对电压的支撑能力越弱；反之，其取值越小，下垂特性越不显著，并联越容易失稳，但电压特性越硬，对电压的支撑能力越强。这一点与构网型储能是一致的。

从图4可以看出，构网型储能的无功控制和调相机的励磁控制极为相似。在暂态过程中积分环节不起作用，KTC等效于式（2）中的Dq，此时图4的电压参考生成环节与式（2）完全一致。值得说明的是，调相机作为一种同步旋转设备，与电网存在电磁耦合关系。当电网故障时，其无功响应是瞬时的、自发的，反映了同步电网自身的电气特征。构网型储能作为电力电子设备，通过模拟同步机的转子运动模型和无功-电压下垂特性方程，来实现与调相机一致的暂态过电压抑制效果。

2.2 最大无功输出能力对比

调相机在不同阶段下对最大无功输出能力的影响因素有所区别。在次暂态过程中，其最大无功输出能力与直轴次暂态电抗有关，直轴次暂态电抗越小，瞬时的无功输出能力越大。但受限于定子绕组温升的制约，直轴次暂态电抗不宜过小。

在暂态过程中，调相机的无功出力由自身和励磁系统共同作用。减小直轴暂态电抗和增大强励倍数有利于提高暂态强励过程调相机的无功支撑能力。QGDW 11588—2016《快速动态响应同步调相机技术规范》规定，调相机定子绕组应能承受3.5 倍额定电流持续时间不小于15 s；转子绕组应能承受2.5 倍额定励磁电流持续时间不小于15 s。此外，为了使调相机能适应直流系统送端过电压工况，调相机需具有1.3倍额定电压下进相持续时间不小于1 s的能力。

需要说明的是，调相机在进相和迟相状态下的最大无功输出能力有所区别。迟相运行时的稳态最大无功能力为其额定容量；进相运行时，考虑到机组稳定性因素，吸收系统无功功率的最大容量通常为额定容量的0.5～0.65倍。

构网型储能的短时过流能力主要与变流器的开关管等器件有关。为了充分发挥其瞬时无功支撑能力，通过合理利用开关管的电流裕量来对其硬件短时过流能力进行强化。在实际工程中，其短时最大过流能力通常设计为1.5～3 p.u.，时间最长可达10 s，这与调相机较为接近。与调相机不同的是，其最大容性无功和最大感性无功输出能力是等同的，这对于应对直流系统送端过电压故障是有利的。当输出电流在限流范围内时，构网型储能表现出低阻抗电压源特性；当输出电流超出限流范围时，通常会采用投虚拟阻抗的方式，通过动态调整其内电势来进行限流。

3 仿真试验对比

3.1 GFM-OPC的影响参数仿真

对影响GFM-OPC 故障电压暂态支撑效果的参数Dq和ωq进行分析。搭建RTDS 半实物仿真试验平台，模拟储能系统近区三相电压对称性短路故障。其系统主电路及控制策略初始默认的相关参数分别如图5和表1所示。

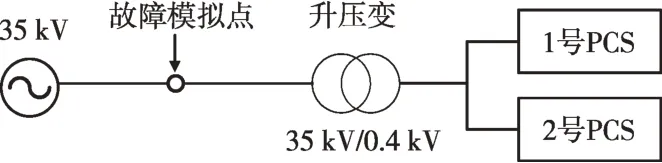
图5 变流器近区电压故障仿真电路Fig.5 The voltage fault simulation circuit in the near area of the converter

1）Dq的影响

通过RTDS模拟线路电压发生扰动的工况（线路电压从1 p.u.跌落至0.5 p.u.，持续100 ms后抬升至1.3 p.u.）。图6 为Dq分别为0.05 和-0.08 时变流器输出无功功率Qo和内电势幅值Eref的变化情况。

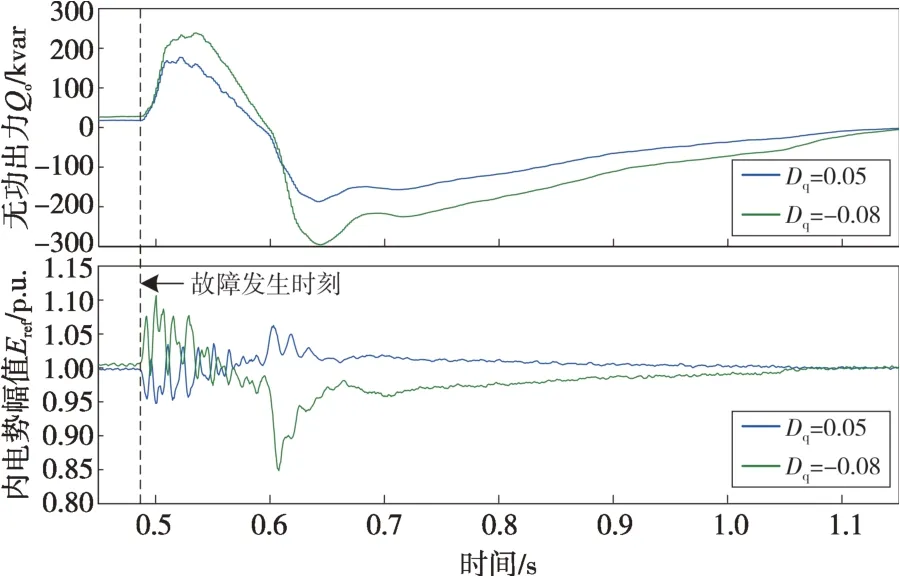
图6 不同Dq下的故障响应波形Fig.6 Fault response waveforms under different Dq

可见，Dq取0.05时，在机端电压Uo先跌落后升高的过程中，Eref会跟随Uo先下降后上升，其无功功率在-190 kvar 和180 kvar 之间变化；Dq取-0.08 时，在此过程中Eref先上升后下降，与机端电压变化方向相反，其无功功率在-300 kvar 和240 kvar之间变化。

Dq取负值意味着故障发生时，变流器将表现出内电势反调的特性，从而进一步提高故障期间变流器的无功出力，起到更强的电压支撑作用。但该值选取的同时需要考虑对多机并联运行稳定性的影响。此外，由于Dq影响稳态时电压下垂所对应的无功出力，因此其取值通常还需要遵循当地电网的要求。

2）ωq的影响

图7为基于表1默认参数下，不同ωq对应的故障响应波形。对于GFM-OPC 而言，当ωq较小时，内电势Eref的变化趋势减缓，系统无法及时响应电压的变化而体现反调特性，导致无功出力减小。

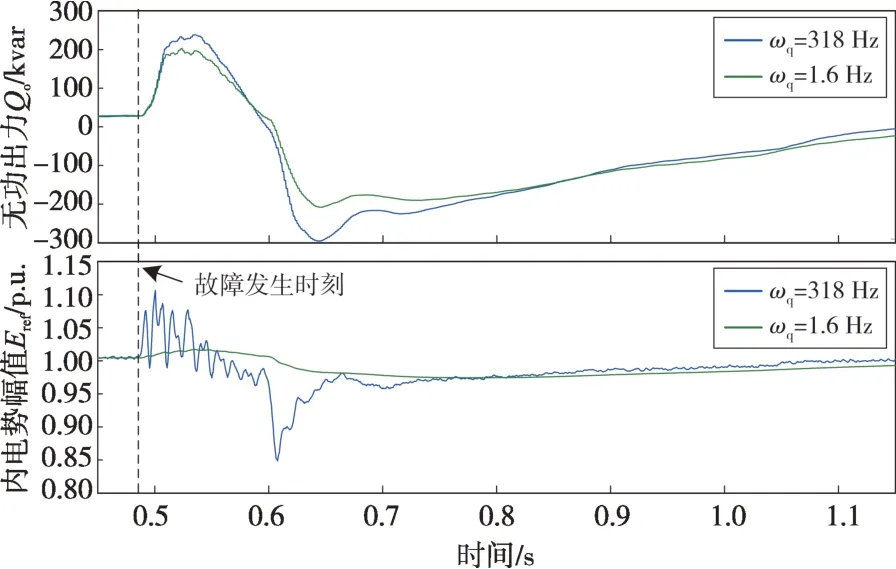
图7 不同ωq下的故障响应波形Fig.7 Fault response waveforms under different ωq

总结以上参数对构网型储能故障电压支撑能力的影响：Dq取较小值时，由于无功-电压的下垂关系，相当于无功下垂特性曲线变硬；当取负值时，相当于让变流器倾向于通过调整内电势使端口电压抬高，加大了自身的支撑能力。对于GFM-OPC，ωq取较大值时，无功滤波较小，相当于电压指令能够快速跟随无功的变化而反调，因此无功响应更快。

3.2 GFM-OPC 与调相机的暂态过电压抑制效果对比

为了进一步对比构网型储能与调相机在直流系统发生故障时的电压支撑效果，以青豫特高压直流系统为例，基于RTDS搭建了换流站-100 MW光伏-50 Mvar 调相机-50 MW 构网型储能的半实物仿真系统，系统结构如图8所示。光伏逆变器采用一台设备倍乘的方式，实际总有功出力100 MW；构网型储能采用两台设备交流侧并联倍乘方式，初始运行在零功率状态，短时过载能力为3倍/10 s，参数如表2所示；构网型策略的默认参数与表1相同；调相机仿真参数如表3所示；励磁控制器采用1.1 节所述的策略，其中电压环串联PID 采用了IEEE的标准ST5B模型，参数如表4所示；光伏电站线路等效短路比为3.9。在直流系统8 000 MW运行状态下，以受端换流站发生直流换相失败故障为例，仿真送端换流站交流侧暂态过电压的情况，故障持续时间100 ms。

表2 光伏电站和构网型储能的仿真参数Table 2 Simulation parameters of photovoltaic power station and GFM energy storage

表3 调相机仿真参数Table 3 Simulation parameters of the synchronous condenser

表4 励磁控制器仿真参数Table 4 Simulation parameters of excitation control

图8 仿真系统结构Fig.8 The simulation system structure

3.2.1 构网型储能与调相机的效果对比

将GFM-OPC 与调相机作横向对比，如图9所示。可见，未投入无功补偿设备时，光伏机端电压在0.536 s 达到最大值0.9 kV；分别投入调相机和GFM-OPC 后，对应的电压最大值分别为0.844 kV 和0.845 kV，对应的无功最大出力分别为-77 Mvar和-74.3 Mvar。

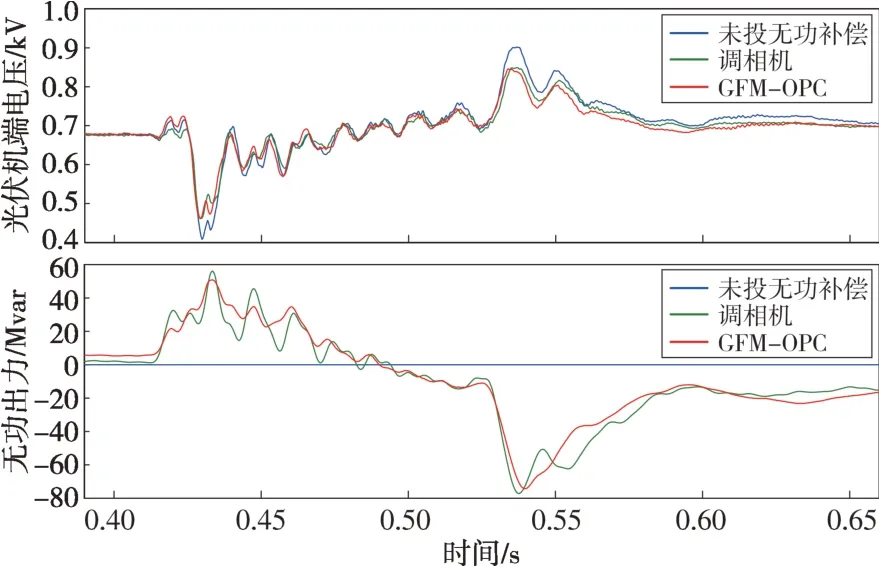
图9 构网型储能与调相机的暂态过电压抑制效果对比Fig.9 Comparison of transient overvoltage suppression effects between GFM energy storage and synchronous condenser

从图9可得，在表1参数下，GFM-OPC的故障电压支撑效果和交流暂态过电压抑制能力均较为接近调相机。在电压跌落和升高期间，该策略的无功出力响应速度与调相机基本保持一致。

3.2.2 构网型储能在不同参数下的效果对比

1）Dq的影响

图10给出了不同Dq下的响应特性。可见，当Dq分别为0.2、0.05 和-0.08 时，电压尖峰最大分别为0.8891 kV、0.857 kV 和0.845 kV，构网型储能的无功出力最大分别为-32.3 Mvar、-42.6 Mvar和-74.2 Mvar。与调相机相比，到达相同出力的延迟时间约为3.2 ms、-1.5 ms 和0 ms。Dq越小，无功出力越接近调相机，因此过电压的抑制效果越好。

图10 不同Dq下GFM-OPC的响应特性Fig.10 Response characteristics of GFM-OPC under different Dq

2）ωq的影响

图11给出了不同ωq下的响应特性。可见，ωq分别为318 Hz和1.6 Hz时，电压最大分别为0.845 kV和0.871 kV，无功出力最大分别为-74.2 Mvar 和-53.2 Mvar；与调相机相比，到达相同出力的延迟时间约为0 ms 和2.1 ms。ωq越大，构网型储能的无功响应速度越接近调相机，因此电压抑制的效果越好。

图11 不同ωq下GFM-OPC的响应特性Fig.11 Response characteristics of GFM-OPC under different ωq

4 结论

本文对GFM-OPC 在无功支撑方面的原理和影响参数进行分析，并以直流系统发生换相失败故障为例，对比了构网型储能和分布式调相机分别接入系统时的暂态过电压抑制能力和效果，从技术角度探讨了构网型储能在无功支撑方面替代“常规储能+分布式调相机”方案的可行性，得到结论如下：

1）GFM-OPC 通过模拟同步机的转子运动方程和无功-电压控制特性，能实现暂态电压波动的有效抑制，体现了良好的无功支撑能力。

2）无功滤波的截止频率越大，GFM-OPC 无功响应速度越接近调相机，电压抑制的效果越好。此外，GFM-OPC 通过改变无功下垂特性可以获得更大的无功出力。

3）整体仿真结果表明，在合适的参数下，构网型储能在无功瞬时响应速度、故障支撑效果、抑制交流暂态过电压能力方面可以与相同容量的分布式调相机取得较为相近的效果。