火电机组交互影响对次同步振荡的作用机理研究
臧德春,赵荣臻,杨 超,祝新驰
(南京南瑞继保电气有限公司,南京 211102)
0 引言
随着电力系统复杂性的不断提高,国内外发生的SSO(次同步振荡)事故中均存在着多机间的交互影响[1-2]。目前在多机SSO研究中,对并列运行同型机组情况的分析较多,大多认为可以将同一电厂相同参数和运行工况的多台机组合并成一台机组[3]。对于非同型机组,多将其他机组等效成电压源与内阻抗的并联。文献[4]仅保留待研究机组,其他机组用次暂态电抗与恒压源表示。这两种做法均忽略了其他机组轴系对待研机组的影响,可能会得出错误的SSO判断[5]。
复转矩系数法作为一种常用的SSO分析方法,物理意义清晰[6],但由于没有直观可信地给出阻尼来源,对于相近扭振频率机组SSO 的轴系影响机理认识仍存在不足。文献[7]将电气阻尼简化为与系统各部分阻抗相关的表达式,但只对单机复转矩系数法进行了简化。
本文研究了次同步频率下火电机组间的交互影响及其对SSO的作用机理。对于复杂多机系统,可以选定一台待研的机组,并将系统其他部分等效成另一台机组,得到类似结构的系统。首先,根据特征矩阵推导出系统的复转矩系数;然后,基于简化复转矩系数法推导了双火电机组简化电气阻尼表达式,显式地建立了系统参数、阻尼及稳定性的关系,分析了系统串补度、机组间电气距离和相近扭振频率对次同步振荡模式的作用机理;最后,通过算例验证了各影响因素对系统次同步稳定性的作用。
1 基于特征矩阵的复转矩系数推导
以图1所示用于SSO研究的IEEE第二标准模型(系统2)[8]两机系统为例进行推导。A、B 机是拥有相近频率的同步电机,通过各自的升压变压器连接在同一母线上,经过串补线路连接到无穷大母线。A 机轴系有4 个轴段,分别为HP(高压缸)质块、LP(低压缸)质块、GEN(发电机)质块和EXC(励磁机)质块;B机轴系有3个轴段,分别为HP质块、LP质块和GEN质块。
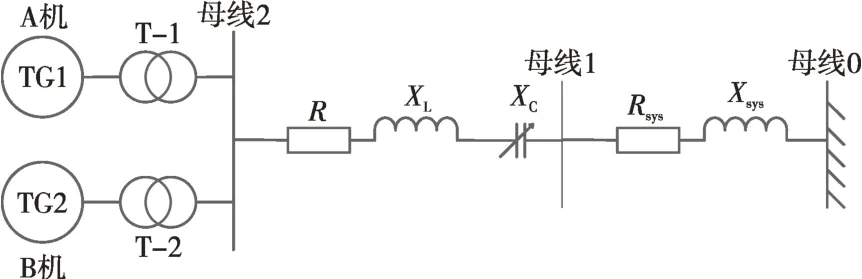
图1 IEEE第二标准模型(系统2)Fig.1 The second benchmark model of IEEE(System 2)
将系统各部分的微分方程、代数方程线性化并联立,可以得到系统状态方程[9],简写为:
式中:I为单位矩阵:Tij为对应系数的简写;p为微分算子;ΔδA和ΔδB分别为A机和B机各质块转子角增量;ΔωA和ΔωB分别为A 机和B 机各质块转速增量;ΔZ为除转子角和转速以外的其他状态变量。
将式(1)代入电磁转矩公式ΔTe=ATeΔZ(ΔTe为电磁转矩,ATe为系数),可得:
式中:ΔTeA和ΔTeB分别为A 机和B 机的电磁转矩;Keij为对应转矩系数,其中i和j取A、B;ΔδA和ΔδB分别为A机和B机GEN质块转子角增量。
对于A、B机,由轴系运动方程可以得到:
式中:ΔTe为电磁转矩;K′m为A、B 机轴系的等值复数力矩系数;Δδ为转子角增量。
将B 机对应的式(3)代入式(2),可推出A 机的电磁转矩为:
其中
式中:K′mB为B 机轴系的等值复数力矩系数;KEA(jξ)为A机的复转矩系数;KeA(ξ)为A机的电气弹性系数;DeA(ξ)为A机的电气阻尼;ξ为自然扭振频率。
根据复转矩系数法原理[10],对于A 机,在满足电气弹性系数与机械弹性系数之和为0,即KeA(ξ)+KmA(ξ)=0 的轴系任何一个自然扭振频率ξ附近,如果A机电气阻尼和机械阻尼之和小于0,即DeA(ξ)+DmA(ξ)<0,则在此频率下系统会发生SSO,否则系统稳定。B机同理。
2 双机系统简化复转矩系数推导
上文推导的电气复转矩系数无法显式表达其他机组轴系影响待研机组阻尼的途径,本章在其基础上进一步推导复转矩系数的简化表达式。
在图1所示系统中,串联电容方程[11]为:
其中
式中:ΔuC,xy为线路串联补偿电容电压变化量;ΔiA,xy和ΔiB,xy分别为A 机和B 机的支路电流变化量;C为串联补偿电容。
无穷大线路方程[12]为:
其中
式中:R和L分别为线路电阻和电感;ΔuaT,xy为公共母线电压变化量。
A机升压变压器方程[13]为:
其中
式中:RTA和LTA分别为A 机变压器等效电阻和电感;ΔuA,xy为A机出口电压变化量。
同理,B机升压变压器方程为:
式中:ΔuB,xy为B机出口电压变化量。
A机电磁侧xy轴方程[14]为:
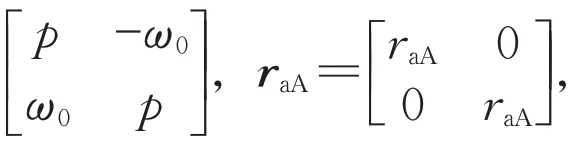
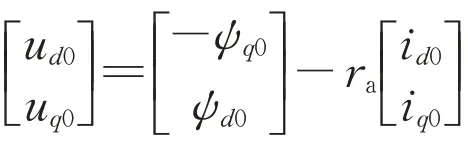
同理有:
式中:Δidq,j为j机的支路电流dq轴分量变化量;kiaδa、kiaδb、kibδb、kibδa为系数。
那么,由ΔTe=[-ψq0ψd0]Δidq可计算A机的电磁转矩如下:
联立A、B 机对应的式(16),并考虑到式(4)的形式,可得:
其中
式中:ψdB0和ψqB0分别为B 机磁链初值d、q轴分量。
那么,A机的电气阻尼为:
式中:DeAA和DeAD为电气阻尼的两个组成部分,DeAA表示待研机组通过系统电路部分产生的电气阻尼,DeAD表示其他机轴系对待研机组电气阻尼产生的影响。
3 交互影响和稳定性分析
由式(19)可以看出,待研机组的电气阻尼可以分为DeAA和DeAD两部分。分析系统参数可知,DeAA一般相对较大,对待研机组电气阻尼影响较大。其他机组对待研机组次同步频阻尼的影响通过两个部分来起作用,第一个部分是其他机组的内阻抗和接入阻抗等电磁部分改变了从待研机组外部次同步频阻抗,第二个部分是其他机组轴系通过系统各部分阻抗产生的阻尼。目前多机SSO研究中采用将其他机组等效成电压源的方法,只计及上述第一个部分的影响,而忽略了第二个部分的影响,从而导致某些情况下做出错误的SSO判断。
观察式(18)表征的KeAD可以发现,该影响主要集中在其他机组的自然扭振频率附近。这是因为K′mB一般较大,可以忽略其后的相加项,并将其他乘积项看作对K′mB的放大系数KeADp,而K′mB在自然扭振频率处等于零,取倒数后会产生突变,再乘放大系数便会造成电气阻尼的较大变化。
经上述分析可知,待研机组电气阻尼在其他机组轴系自然扭振频率处一定会受到影响,这与两机是否存在相同或相近扭振频率没有关系。但该影响是否会涉及待研机组的稳定性,却和两机是否存在相同或相近的扭振频率有关。因为只有扭振频率接近,其他机组造成的这种电气阻尼变化才能影响到待研机组扭振频附近的阻尼,进而影响待研机组的稳定性。
火电机组的轴系参数是固定的,影响火电机组间交互的主要是放大系数KeADp,由于轴系的影响是通过电路来放大,而从电路角度看,A、B机是对称的,因此两机同频率下的放大系数近似相等。从dq轴阻抗的角度来看,KeADp为两个分流系数的乘积,A、B机的分流系数为线路阻抗与系统阻抗和(即线路阻抗、变压器阻抗、电机内部阻抗之和)的比值。因此,线路阻抗越大,变压器支路阻抗越小,即机组间电气距离越近,放大系数越大,其他机组对待研机组的影响越大。
4 算例分析
对于图1所示的两机系统,分析其他机组轴系及不同参数变化对交互影响及多机SSO 的作用机理。使用MATLAB 进行特征值、阻尼及参数计算,并进行PSCAD仿真。
4.1 其他机组轴系对多机SSO的影响
串补度Kcom=0.4,忽略和考虑A、B机轴系对另一台机的影响时,A、B机的电气阻尼曲线如图2所示。特征值和Km+Ke=0 时的总阻尼Dm+De列于表1中。
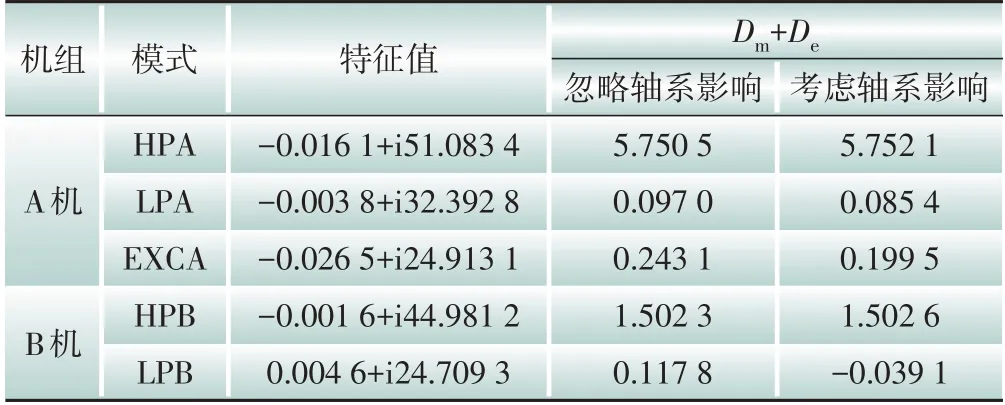
表1 忽略和考虑轴系影响时的特征值和Km+Ke=0时的Dm+DeTable 1 Eigenvalues with and without the influence of shafting under consideration and Dm+De when Km+Ke=0
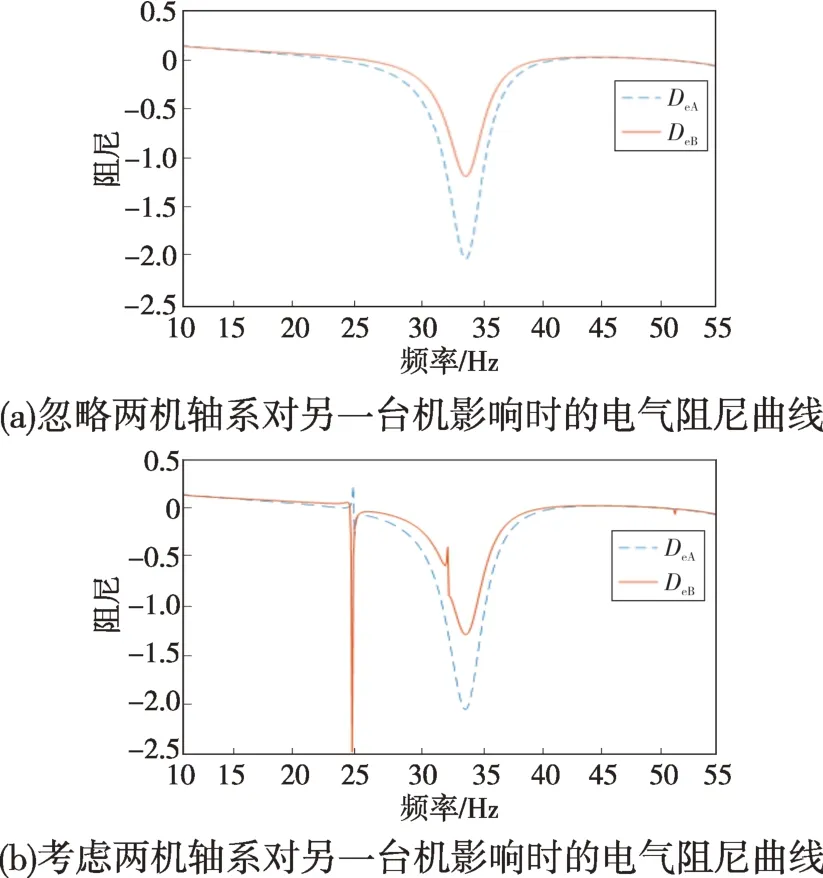
图2 忽略和考虑两机轴系对另一台机影响时的电气阻尼曲线Fig.2 Damping waveforms with and without the influence of the shaftings of two units on another unit under consideration
由图2 可以看出,不考虑轴系交互影响时,A、B机只在系统谐振点附近有一个极小值。考虑轴系交互影响后,在另一台机的扭振频率处,待研机组的电气阻尼会出现剧烈的变化,在相近扭振频率处的变动幅度最大。这验证了其他机组轴系对待研机组的影响集中在其他机组轴系自然扭振频率处,与A、B机是否存在相同或相近的扭振频率没有关系。LPB(B 机LP)模式的特征值实部为0.004 6,系统是失稳的,考虑轴系交互影响时,Km+Ke=0频率处的Dm+De为-0.039 1,与特征值判断一致。但不考虑轴系交互影响时,LPB模式下Km+Ke=0 频率处的Dm+De为0.117 8,与特征值判断结果相悖,这说明不考虑轴系交互影响有时会得出错误的结论。
由图2和表1可以看出,只有在相近扭振频率处,轴系交互影响才有可能会引发SSO。这是由于交互影响造成的阻尼变化只在很小的频率范围内,只有在相近扭振频率处其他机组轴系才能影响到待研机组的阻尼。图3所示的转速曲线和FFT(快速傅里叶变换)频谱图显示A、B机发生振荡,振荡频率接近25 Hz,与分析一致。
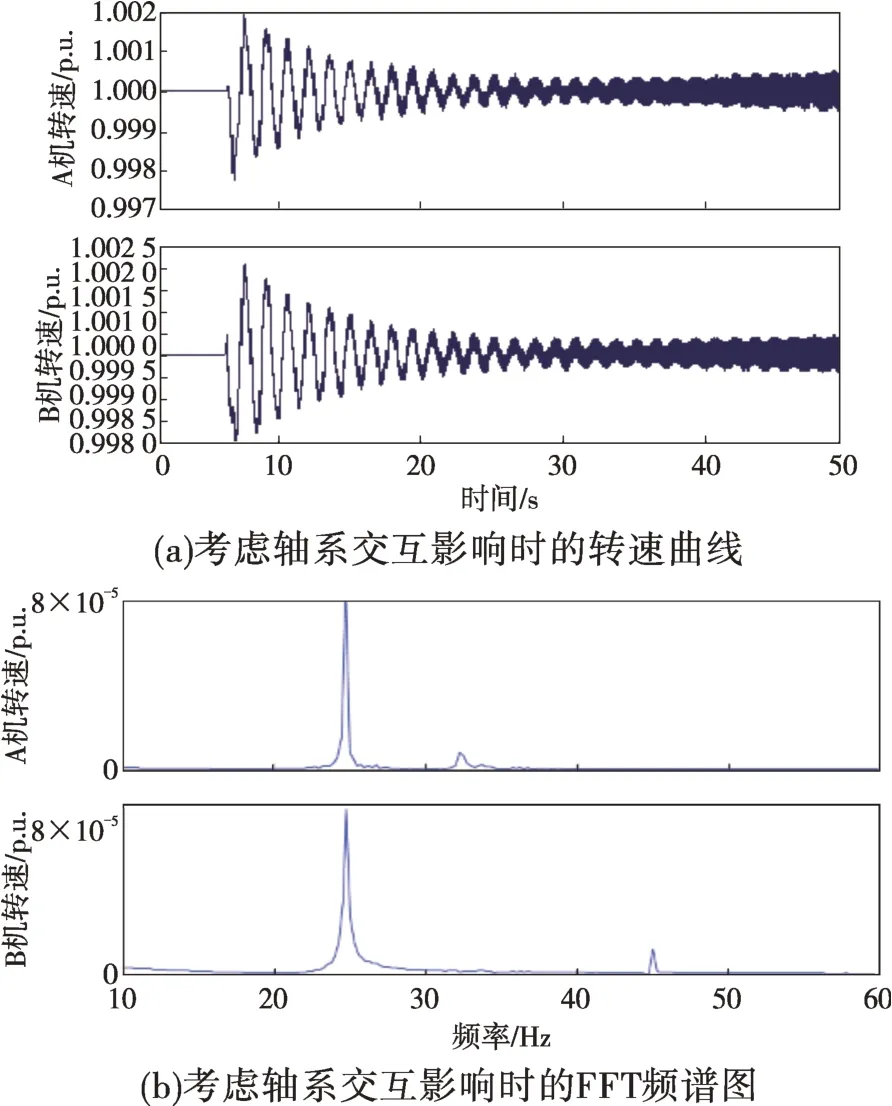
图3 考虑轴系交互影响时的转速曲线和FFT频谱图Fig.3 Rotational speed curves and FFT spectrum with shafting interaction under consideration
4.2 系统参数对多机SSO的影响
4.2.1 串补度的影响
保持其他参数不变,改变串联补偿电容值,获得不同串补度时A、B机的电气阻尼曲线如图4所示,对应系统特征值和Km+Ke=0 时的总阻尼Dm+De列于表2中,图5给出了对应串补度的转速曲线。

表2 不同串补度时系统特征值和Km+Ke=0时的Dm+DeTable 2 Eigenvalues of the system with different series compensation levels and Dm+De when Km+Ke=0
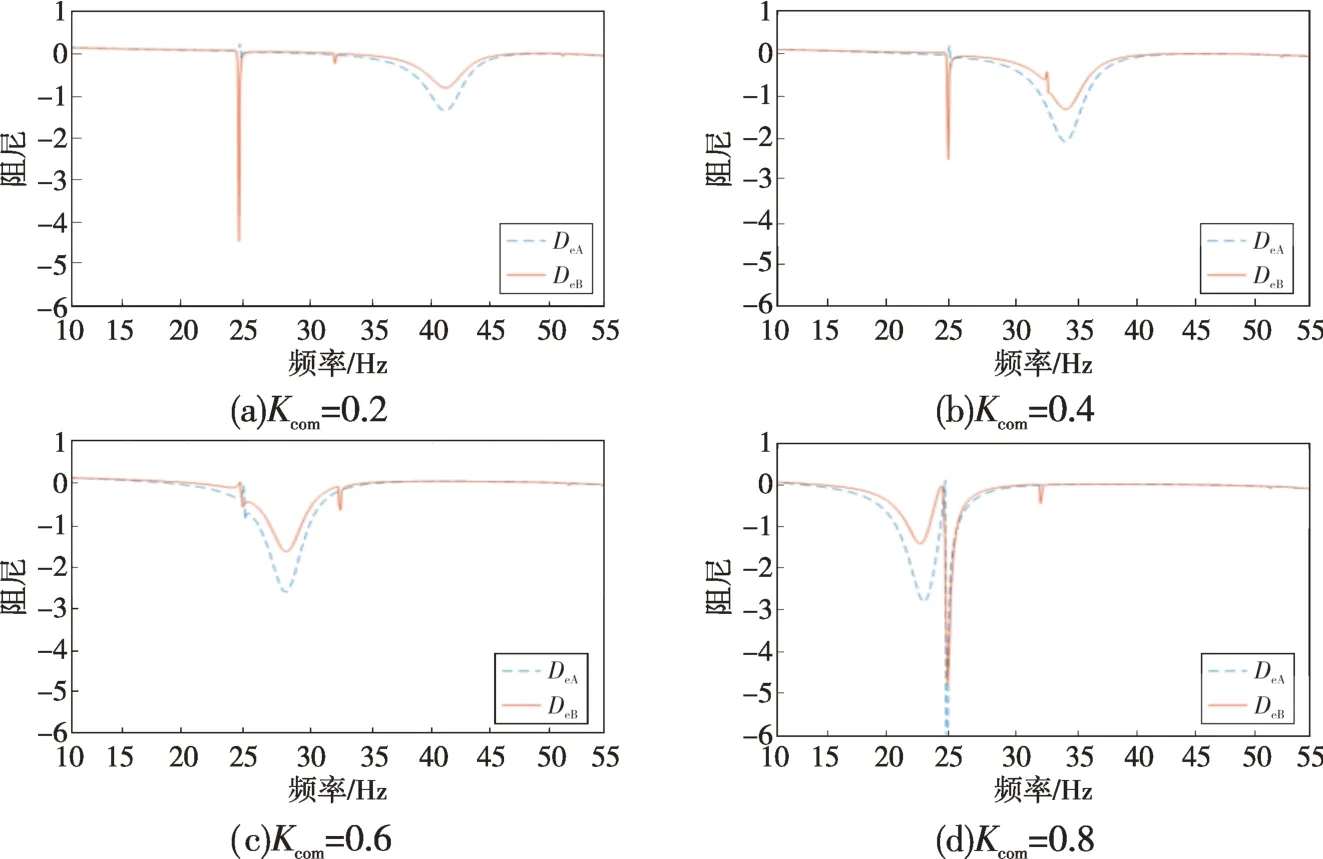
图4 不同串补度时两机的电气阻尼曲线Fig.4 Electrical damping curves of two units with different series compensation levels
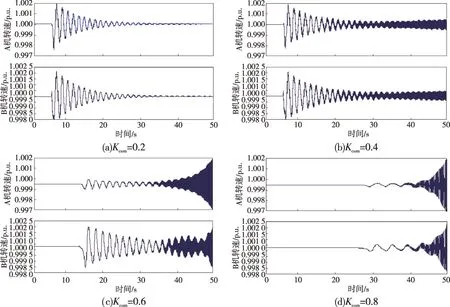
图5 不同串补度下的转速曲线Fig.5 Rotational speed curves with different series compensation levels
由表2中的计算结果可知,当串补度为0.2时,所有Km+Ke=0 时的总阻尼Dm+De都为正值,系统稳定。当串补度逐渐增大,数值为0.2~0.6 时,由图4可以看出,系统谐振频率离相近扭振频率越来越近。受谐振频率接近的影响,两机相近扭振频率处的电气阻尼均不断减小,说明系统会发生频率为24.5 Hz左右的SSO,且越来越严重。
当串补度继续增大为0.8 时,图4 显示谐振频率继续减小,比相近扭振频率还要小。表2显示A机相近扭振频率下的Dm+De增大为正值,模式变为稳定,而B 机相近扭振频率下的Dm+De继续减小,加剧了SSO。根据图6 给出的忽略和考虑轴系影响时的电气阻尼曲线可以发现,在相近扭振频率处,忽略轴系影响的阻尼曲线还处于谐振频率引起的极小值的恢复期。考虑轴系影响后,相近扭振频率处电气阻尼发生突变。A机扭振频率处的电气阻尼处在突变极大值附近,Dm+De为0.049 1,模式变得稳定;而B机的Dm+De为-1.234 9,模式仍失稳。这与串补度为0.4时的分析结论一致,即忽略轴系影响会得出错误的SSO判断。表2中的特征值和图5中各种串补度下的转速曲线均与复转矩系数法分析结果一致。
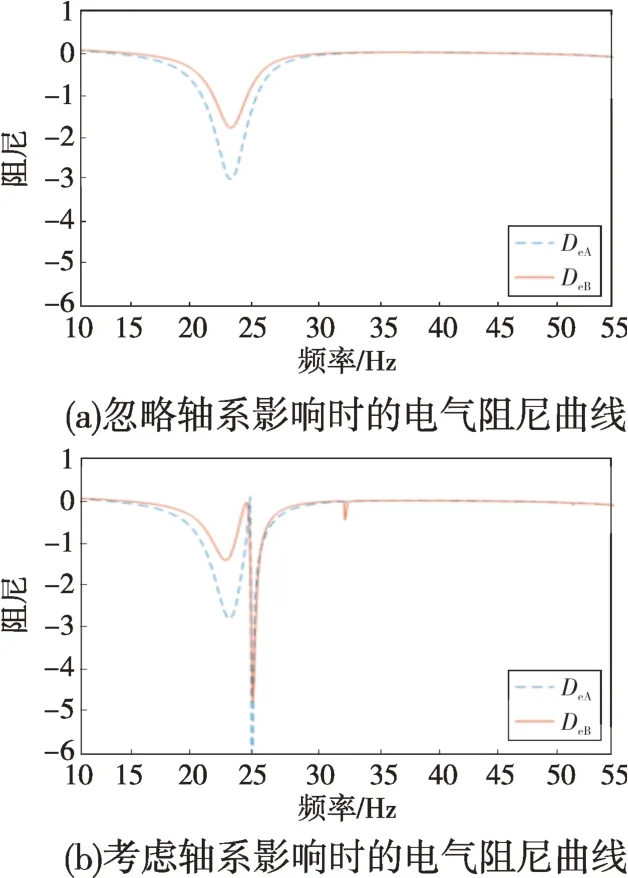
图6 Kcom=0.8时忽略和考虑轴系影响时的电气阻尼曲线Fig.6 Electrical damping curves with and without the influence of shafting under consideration when Kcom=0.8
4.2.2 机组间距离的影响
保持Kcom=0.4 不变,改变机组间距离,等效地改变A、B 机连接的变压器支路阻抗,A、B 机的电气阻尼曲线如图7所示。Km+Ke=0时的总阻尼Dm+De列于表3中。

表3 不同机组间距离时两机系统特征值和Km+Ke=0时的Dm+DeTable 3 Eigenvalues of the two units with different unit spacings and Dm+De when Km+Ke=0
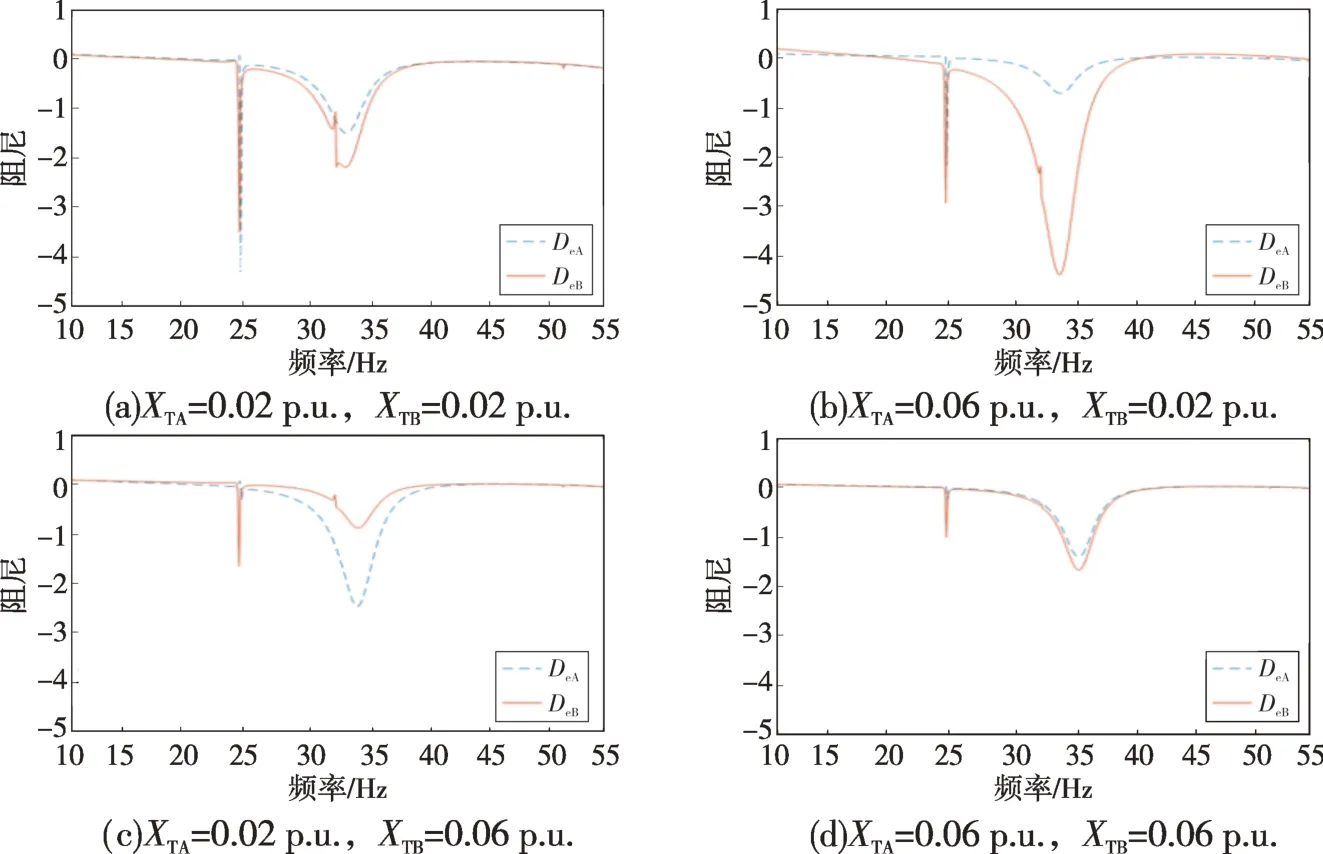
图7 不同机组间距离时两机的电气阻尼曲线Fig.7 Electrical damping curves of two units with different motor spacings
由图7 可以看出,A、B 机电气距离越大,电气阻尼曲线受轴系交互影响出现的变动就越小。这也验证了第3 章的分析,即两机电气距离越大,分流系数越小,KeADp和KeBDp就越小,轴系产生的交互影响就越小。
进一步观察系统稳定性,分析表3 可以发现,保持B机变压器等效电抗XTB不变,增大A机变压器等效电抗XTA,EXCA(A 机励磁机)模式总阻尼基本不变且均为正值,而LPB 模式的总阻尼不断增加,稳定性有所提高。当XTA=XTB=0.06 p.u.时,LPB 模式Dm+De变为正值,系统稳定。当XTA不变,增大XTB时,EXCA模式的Dm+De基本不变且大于零,而LPB模式的Dm+De增加,稳定性提高。总体来看,系统稳定性会增强。这主要是因为LPB 模式与系统谐振频率相距较远,稳定性基本只受两机间的交互作用影响,而随着A、B机间电气距离的增加,交互作用必然减弱,该模式下系统也就愈加稳定。表3给出的相应的特征值和图8 给出的XTA=XTB=0.02 p.u.和XTA=XTB=0.06 p.u.时的转速曲线均与复转矩系数法得到的结果一致。
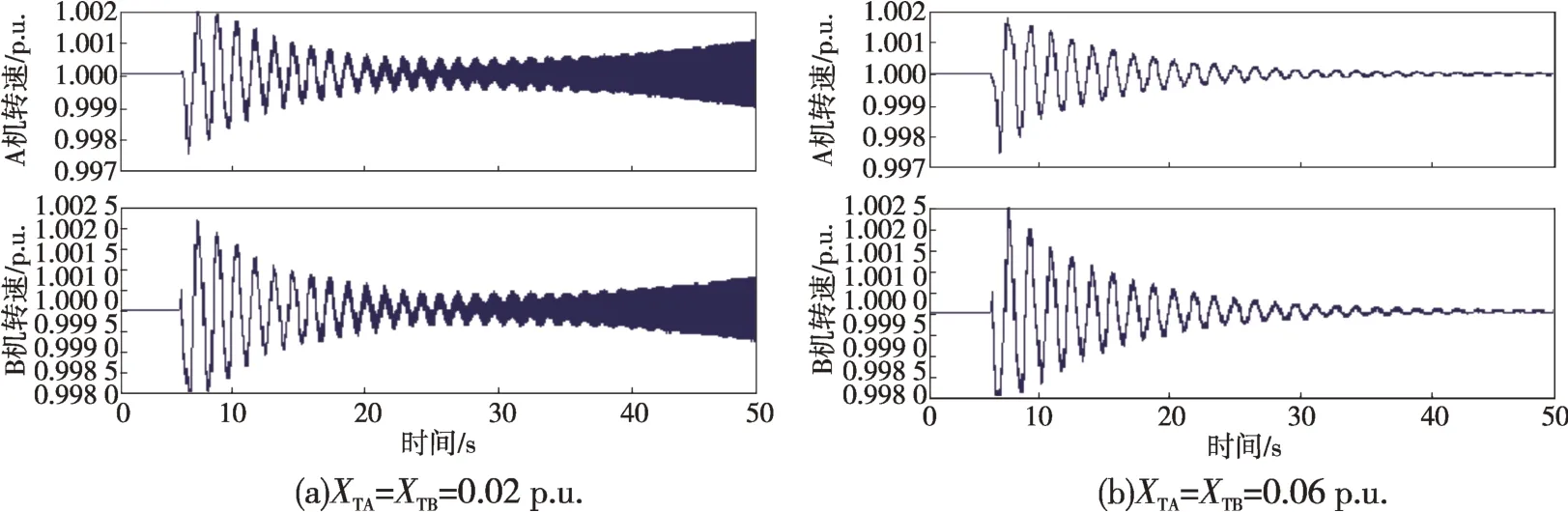
图8 不同机组间距离时转速曲线Fig.8 Rotational speed curves with different unit spacings
4.2.3 相近扭振频率的影响
保持Kcom=0.4 不变,改变相近的自然扭振频率,获得对应情况下A、B机的电气阻尼曲线如图9所示,对应的系统特征值和Km+Ke=0 时的Dm+De列于表4中。

表4 相近扭振频率变化时系统特征值和Km+Ke=0时的Dm+DeTable 4 System eigenvalues with change of similar torsional vibration frequency and Dm+De when Km+Ke=0
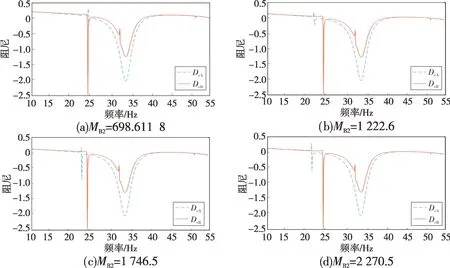
图9 相近扭振频率变化时两机的电气阻尼曲线Fig.9 Electrical damping curves of two units with the change of similar torsional vibration frequency
由图9和表4可以看出,随着B机扭振频率的减小,两机的频率相距越远。在LPB 机械参数MB2=1 746.5 时,A、B 机的频率差已大于2 Hz,此时再增加频率差,A 机特征值和Dm+De实部几乎不发生变化。这是因为轴系交互影响引起的阻尼变化在B 机频率处还未开始,而在A 机频率处已经恢复,说明此时B 机轴系对A 机的稳定性不再产生影响。这与第3章中的分析一致,即其他机组轴系是否会影响待研机组的稳定性和两机存在相同或相近频率有关。根据本算例,可以认为当A、B机的扭振频率差大于2 Hz后,不需要考虑其他机组轴系的影响。随着两机自然扭振频率差的加大,原来发生SSO 的系统稳定。图10 给出了MB2=698.611 8和MB2=2 270.5时的转速曲线,与分析结果一致。
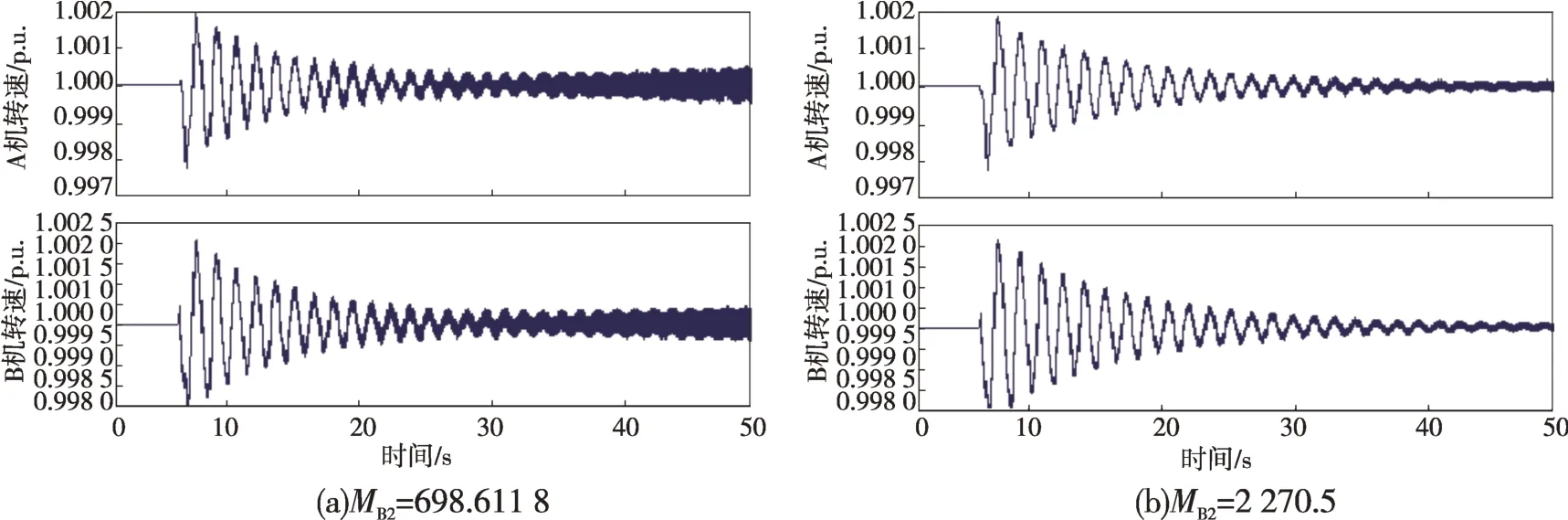
图10 相近扭振频率变化时转速曲线Fig.10 Rotational speed curves with the change of similar torsional vibration frequency
5 结语
本文以IEEE 第二标准测试(系统2)为研究对象,分析了多火电机组间,尤其是轴系间的交互影响及其对SSO 的作用。首先,对单机系统简化复转矩系数法进行扩展,推导了所研究系统的简化复转矩系数,分析结果表明,其他机组通过两个部分对待研机组次同步频阻尼产生影响,第一个部分是其他机组的内阻抗和接入阻抗等电磁部分改变从待研机组往外看的次同步频阻抗;第二个部分是其他机组在其自然扭振频率附近的阻尼变化会作用于相同频率处的待研机组电气阻尼。当两机存在相同或相近频率时,该项会影响到待研机组的稳定性,导致得到错误的SSO 判断。进一步利用简化复转矩系数研究了系统参数对交互作用和系统稳定性的影响,发现第一个部分电磁部分主要受串补度的影响,通过改变线路谐振频率来影响待研机组的电气阻尼。而当机组间电气距离或扭振频率差增大到一定程度时,机组轴系间交互作用基本可忽略不计。

