基于谱聚类的主动配电网多时间尺度无功优化策略
闫丽梅,丁泽华
(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)
0 引言
“双碳”目标背景下,大规模的DG(分布式电源)逐渐接入配电网的馈线末端,推动配电网形态向ADN(主动配电网)转变的进程。ADN由于DG的接入,具备主动调节无功的能力,提高了电网可靠性,减少了配电网建设成本。但是,DG出力存在不确定性及难以与传统无功调控设备协调控制的问题,给ADN的无功功率优化带来了新的挑战[1-7]。目前离散型调控设备OLTC(有载调压变压器)、SCB(并联电容器组)等仍是保证配电网电能质量和运行经济性的重要手段[8]。因此,如何使DG 与传统无功调控设备相结合、共同参与ADN的动态无功优化,对保证ADN安全经济运行、降低ADN无功补偿设备投资具有重要意义[9-12]。
针对ADN无功优化这一问题,学者们选择了不同方法。文献[13-14]分别以DG 运行成本和网损最小为目标函数,建立配电网无功运行优化模型;文献[15]以DG消纳最大化、电网电压偏差最小及网损最小为目标函数,建立各个分区的子优化模型。上述文献单独考虑DG选址及无功优化问题,并未考虑DG与离散设备投切动作相结合。文献[16]将离散型调控设备的动作次数作为正常的约束来求解,满足了离散设备动作次数约束,但优化问题中同时存在离散变量和连续变量,变成了非线性混合整数规划问题,求解方法复杂、难度大;为提高求解速度,通常需要在保障解的趋优性同时进行简化处理。文献[17]为避免离散设备动作次数超出约束,将相关设备动作成本纳入目标函数。文献[18]以网损成本,OLTC和SCB、可再生DG的无功成本作为无功优化目标函数,日内矫正采取模型预测控制的方式;因动作成本直接影响动作次数,权重系数选择不当会导致离散设备动作次数过多或过少;而日内实时反馈对于通信设备要求极高,目前多数配电网无法普及。文献[19]提出一种松弛-聚类-校正无功优化解耦策略,松弛离散变量的动作次数约束得到静态解以后,采用K-means 聚类的方法来满足时间耦合性;然而,K-means 聚类方法并不适用于离散设备动作序列聚类。文献[20]采用灰色关联度映射方法划分时段,在同一时段内协同优化不同类型变量,然后固定多个时段内SCB 和OLTC 的状态,进行二次静态无功优化校正;但该研究没有考虑预测值与实际值的误差会导致电压波动的问题,没有进行日内动作优化。文献[21]提出一种日前无功/电压优化控制与实时自治控制相结合的混合时间尺度无功/电压控制方法;由于DG 出力具有波动性,仅依赖本地实时信息的实时自治控制策略虽然可靠性高,但缺乏整体协调性,不是全局最佳方案。
基于上述分析,本文提出一种日前无功-电压优化与DPV(分布式光伏)逆变器实时自治控制相结合、基于谱聚类的多时间尺度动态无功-电压优化策略。该策略的核心是:在日前优化过程中解耦离散设备时间耦合性,将动态无功优化问题化简为非线性规划问题,得到离散设备静态最优档位序列,再通过谱聚类的方式得到离散设备动态最优档位序列。在日内实时优化过程中,为了应对DPV 出力的波动性及预测误差导致的电压波动,建立基于DPV逆变器改进就地控制策略的日内实时优化模型,充分利用DPV逆变器的无功调节能力,避免电压越限情况的发生。针对化简后的模型求解问题,本文通过SNS(社交网络搜索)算法求解模型,有效避免了传统算法容易陷入局部最优的问题。最后,以IEEE 33 节点系统为算例,仿真验证所提策略的有效性与优越性。
1 多时间尺度动态无功优化策略思路
配电网各时段优化仅需要考虑当前时段的状态,但是配电网前一时段的状态会对下一时段产生影响,同时离散设备的调控次数在日内存在约束。因此,本文提出多时间尺度无功优化策略。首先,根据小时级的光伏出力、负荷预测数据,将离散设备日内实时档位解耦成为连续变量,将动态优化问题转变成为多个时间段的静态优化问题,以ADN运行的安全性、经济性为目标函数建立日前无功优化模型。针对传统元启式算法求解优化问题时收敛速度慢、容易陷入局部最优、求解精度低的问题,本文采用SNS 算法来求解优化问题,得到离散设备静态最优档位序列;然后,通过谱聚类算法进行耦合,得到满足离散设备日内动作次数约束的离散设备动态最优档位序列,结合一种改进的DPV逆变器就地控制策略,以平均电压偏差最小为目标函数建立日内无功优化模型,尽量抑制由于日内实际光伏出力、负荷值与预测值的误差导致的电压波动,使各节点电压与日前优化结果的差值更小。具体优化策略框架如图1所示。
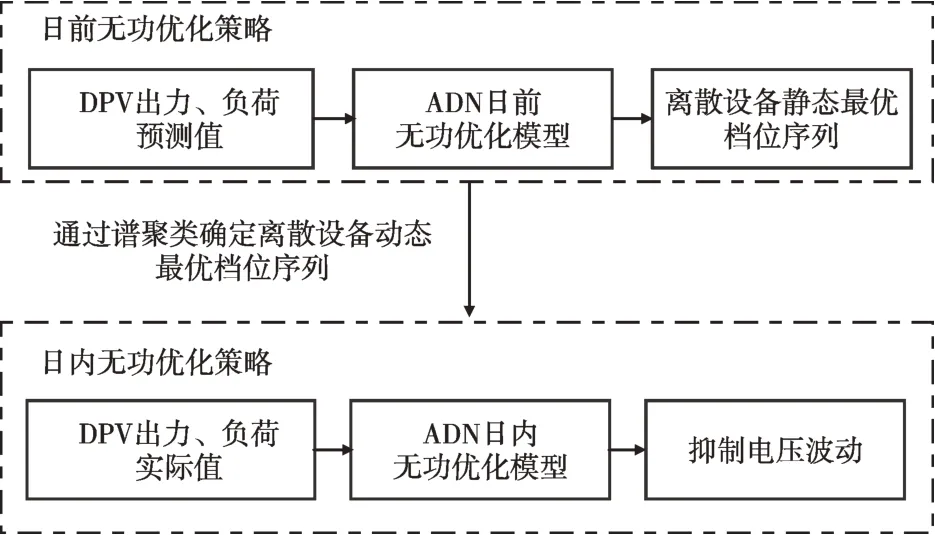
图1 ADN多时间尺度无功优化策略框架Fig.1 The framework of a multi-timescale reactive power optimization strategy for ADN
2 ADN日前无功优化模型
2.1 目标函数
由于DG出力的不确定性,传统配电网中的网损与电压偏差作为无功优化目标函数无法完全适应ADN 调控的需求。考虑DG 并网以后会极大地影响馈线末端电压质量,本文采用风险偏好型效用函数[22]定量评价电压波动严重程度,将配电网的网损、电压偏差和电压波动严重程度3项指标作为ADN日前无功优化模型的目标函数,并考虑各个目标函数间单位、数量级并不相同,归一化后建立优化适应度函数进行评估。
1)配电网网损f1为:
式中:H为支路数;Ph,t和Qh,t分别为t时段h支路有功功率和无功功率;Rh为h支路的电阻;Uh,t为t时段h支路的首端电压。
2)平均电压偏差f2为:
式中:N为节点数;T为一个调度周期内的时段数;Ui,t为t时段节点i的电压;UNi为节点i的额定电压。
3)电压波动严重程度。t时段配电网任一节点的不稳定性ci,t为:
式中:7%为最大允许电压偏差。
t时段节点i的电压波动严重程度bi,t为:
电压波动严重程度f3为:
4)各目标函数归一化处理。考虑各个目标函数间单位、数量级并不相同,归一化处理如式(6)所示:
式中:Fr为归一化后的目标函数;fr为原目标函数;frmin为单目标优化结果;frmax为未优化的结果。
5)加权优化适应度函数。加权优化适应度函数中,权重系数的确定采用层次分析法,按文献[23]的步骤以重要程度(配电网网损>电压偏差>电压波动损耗)构造判断矩阵A:
经计算,3 个子目标函数所对应的权重系数分别为ϖ1=0.594 9、ϖ2=0.276 6、ϖ3=0.128 5。为验证权重系数的合理性,需进行一致性检验。当判断矩阵A对应的随机CR(一致性比率)值小于0.1时,方可通过一致性检验,否则需调整判断矩阵A中的元素,重新计算权重系数。经检验,判断矩阵A对应的CR 值为0.037<0.1,通过一致性检验,故该权重分配是合理的。目标函数为:
2.2 约束条件
1)潮流约束为:
式中:Pi和Qi分别为节点i上流入的有功和无功功率;Ppv,i和Qpv,i分别为节点i上DPV的有功和无功功率输出;Pload,i和Qload,i分别为节点i上负载的有功和无功功率;Qsc,i为节点i补偿网络的无功功率;Gij和Bij分别为节点i与节点j间支路的电导和电纳,θij为节点i和节点j的电压相角差;Ui和Uj分别为节点i和节点j的电压。
2)节点电压约束为:
式中:Ui,min和Ui,max分别为节点i的电压下限和上限。
3)SCB补偿容量约束为:
式中:Qsc,i,min为节点i的最小无功功率;Qsc,i,max为节点i允许的最大无功功率。
4)DPV有功出力约束为:
式中:Ppv,i,t为t时段节点i上DPV 的有功输出;Ppv,i,min和Ppv,i,max分别为节点i上DPV 的最小和最大输出功率。
5)DPV无功出力约束。DPV系统等发出直流或高频交流电的DG需通过逆变器与电网并网,通过控制并网逆变器,DG在向电网提供有功功率的同时也能够提供电网所需的无功功率。DPV 能够提供无功功率的容量约束为:
式中:Spv,i为DPVi的逆变器容量功率,约为额定光伏输出有功功率的1.1 倍;Qpv,i,t为t时段节点i上DPV 的无功输出;Qpv,i,max为节点i上DPV 的最大无功输出。
6)支路容量约束为:
式中:Sh为支路h的功率;Sh,max为支路h允许的最大功率。
3 ADN日内实时优化模型
DPV与传统无功调控设备出力需要进行配合,而离散设备由于动作次数约束而无法实时动作,这就是动态无功优化过程中存在的时间耦合性。因此,在日前的动态无功优化策略中取消了离散调控设备动作次数的约束,解耦时间耦合性,将各个时段视为独立的静态无功优化,得到离散设备24 h静态最优档位序列。
考虑到DPV 连续、随时可调的特点,本文在日前优化结束后,先对离散设备24 h 静态最优档位序列进行谱聚类,得到24 h动态最优档位序列。再在日内考虑负荷及光伏出力的突变导致电压出现波动甚至越限等情况,以15 min 为一个时段,进行日内DPV动态无功优化。
3.1 基于谱聚类的的时段解耦策略
本文根据OLTC 抽头和电容器组的静态最优开关序列,考虑日内动作最大次数约束,通过谱聚类解决时间耦合性,得到它们的动态最优档位序列。与常见的K-means 聚类相比,谱聚类首先没有限制相似性度量用欧氏距离,而是用拉普拉斯矩阵将相似度扩展为任意函数,更加灵活。其次,它将原问题松弛化,用特征值分解的方式获得样本在新空间中的表达。最后,谱聚类能够利用相似度矩阵来进行聚类,因此对于一些没有明显距离度量的数据,也能得到较好的聚类效果。
谱聚类模型的建立包括6个步骤:
1)根据静态最优档位序列构建度矩阵D和邻接矩阵W,由于离散调控设备是要具有时序特性的,仅计算相邻数据dx和dy之间的权重wxy:
2)计算拉普拉斯矩阵L=D-W。
3)构建标准化后的拉普拉斯矩阵S:
4)计算标准化拉普拉斯矩阵最小的k个特征值所各自对应的特征向量g,构建特征向量矩阵G。
5)G中的每一行作为一个k1维的样本,共n个样本,用K-means 聚类方法进行聚类,聚类维数为m(考虑OLTC 和SCB日内动作次数约束进行选择)。
6)得到簇划分C=(C1,C2,…,Cm)。
谱聚类只需要数据之间的邻接矩阵,因此对于处理稀疏数据的聚类很有效。
3.2 日内DPV动态无功优化策略
通过上述方法确定了离散调控变量24 h 动态最优档位序列,但是实际数据与预测数据之间的误差很容易导致ADN电压波动。以日前动态无功优化结果、离散调控变量24 h 动态最优档位序列为基础,考虑到充分利用DPV的无功调控能力以及无法全域通信实时调控的实际情况,采用本地自适应电压调节策略进行控制。
3.2.1 DPV日内调控模式
由文献[24]可知:仅通过无功进行调控的DPV 可能会出现无功容量不足、并网节点电压仍然越限的情况;仅通过有功削减的调控方法,会导致DPV无法工作在MPPT(最大功率点跟踪)模式,经济性不够。针对上述情况,本文采用一种本地自适应电压调节策略。
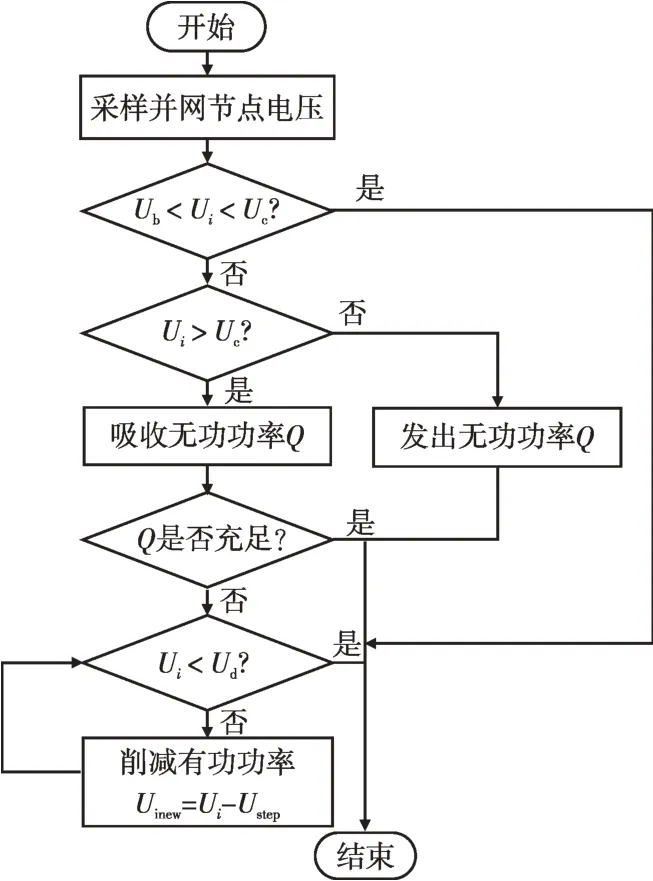
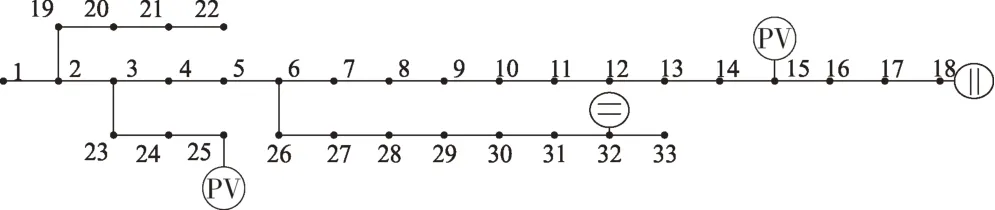
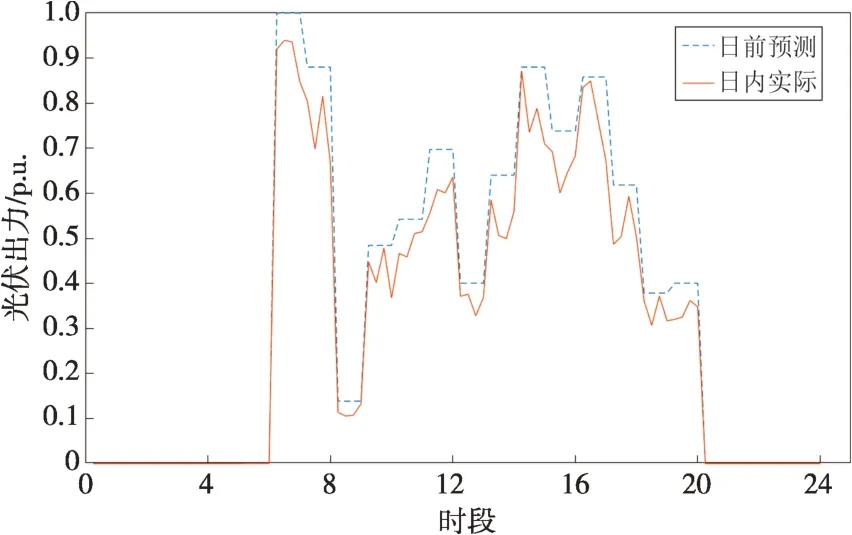
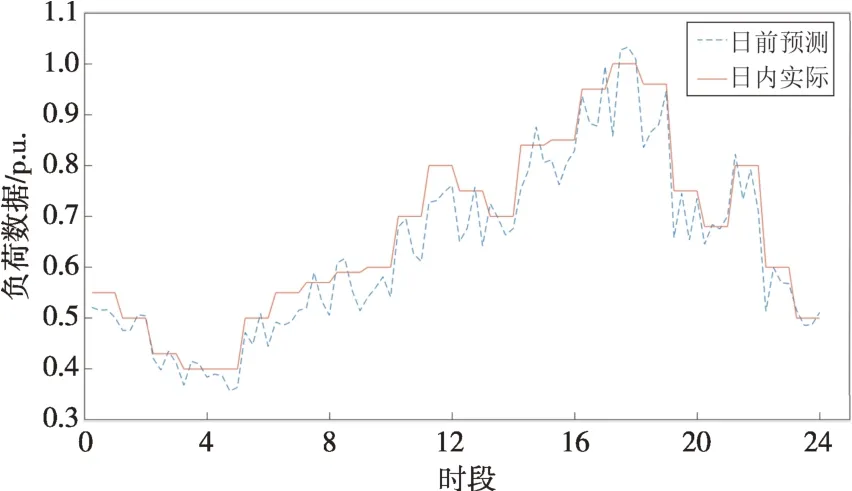
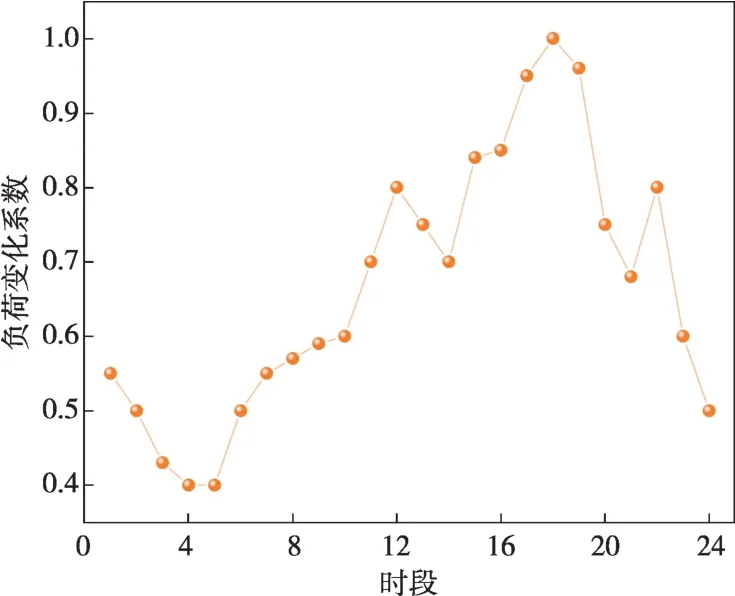
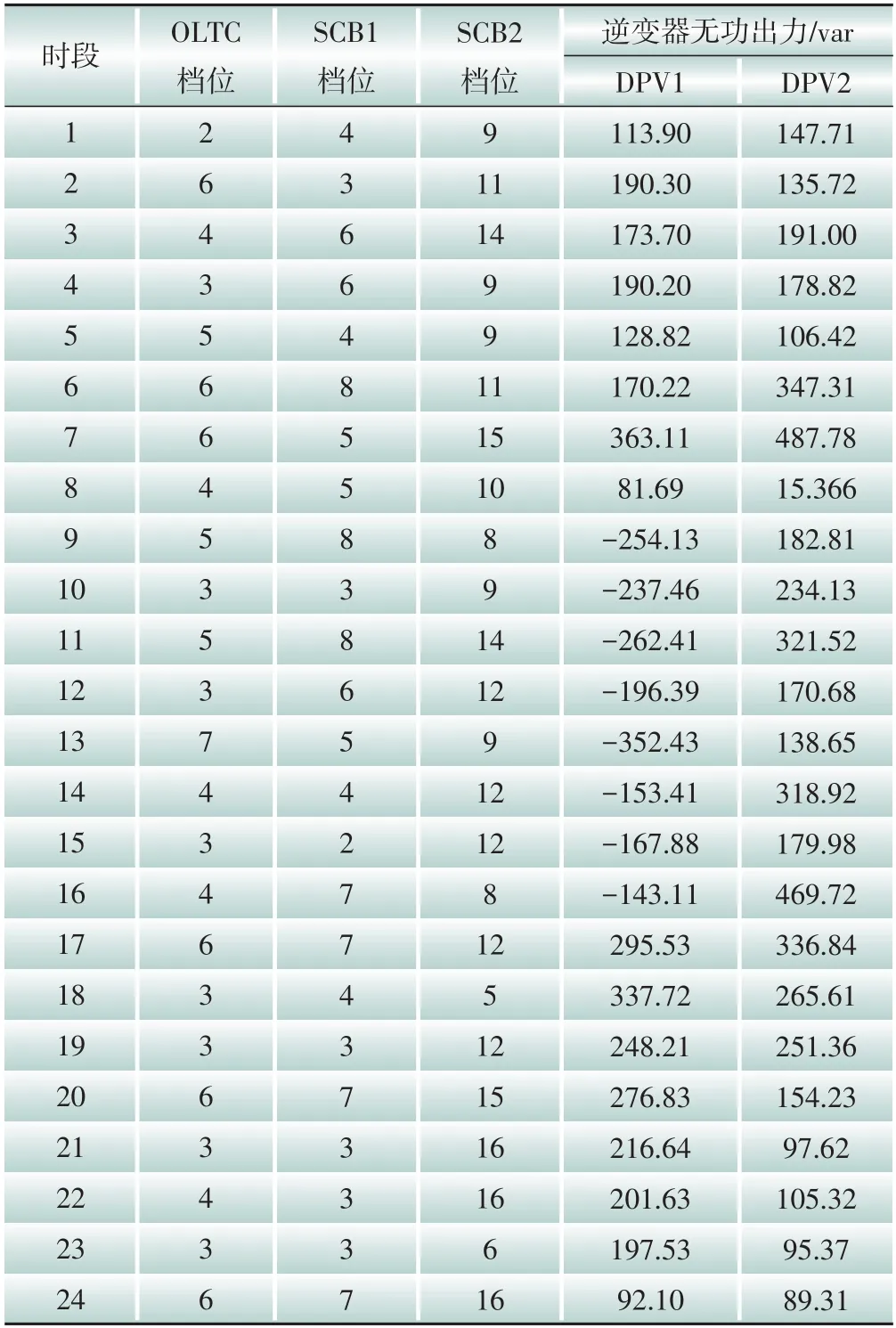
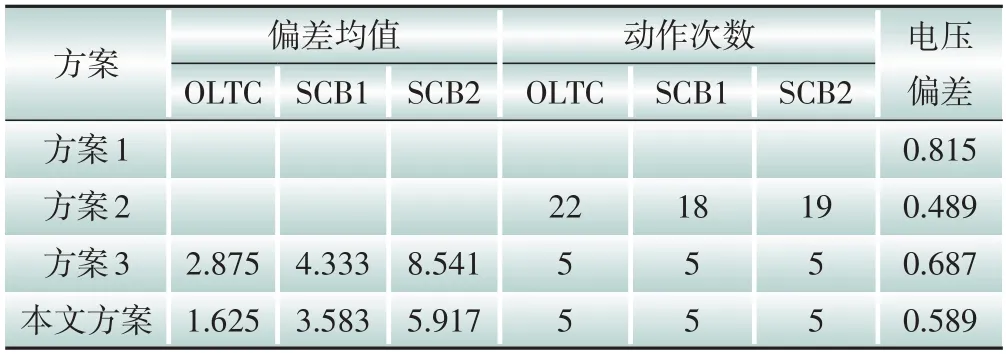
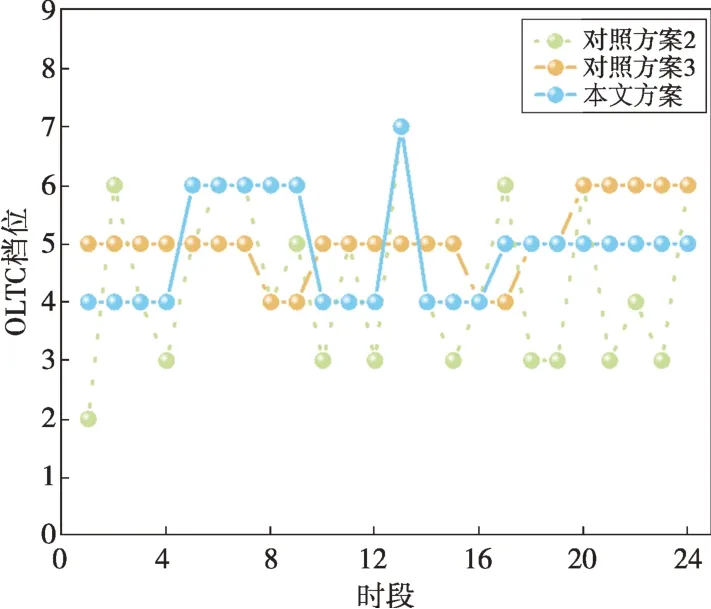
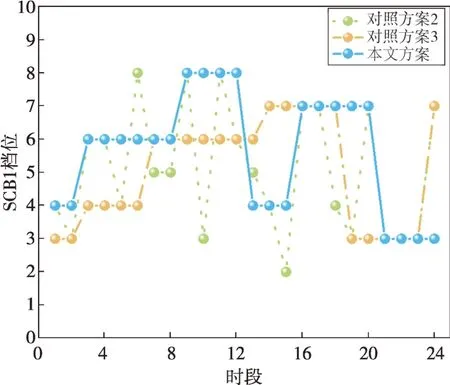
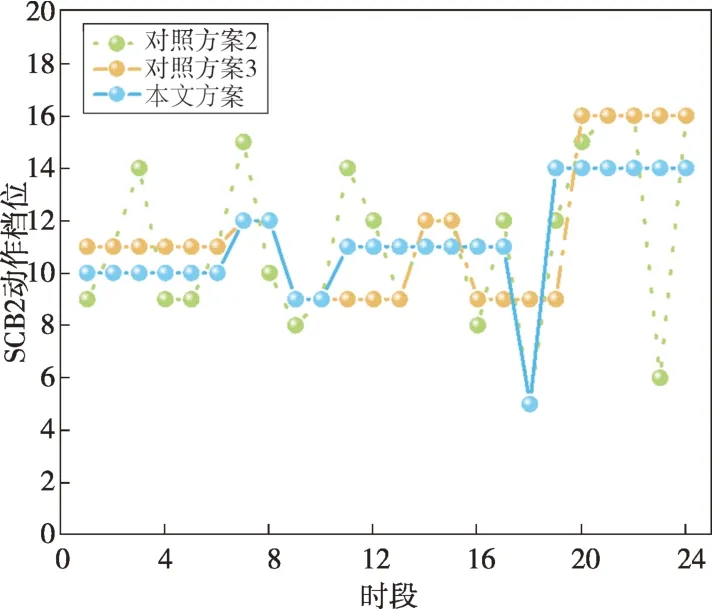
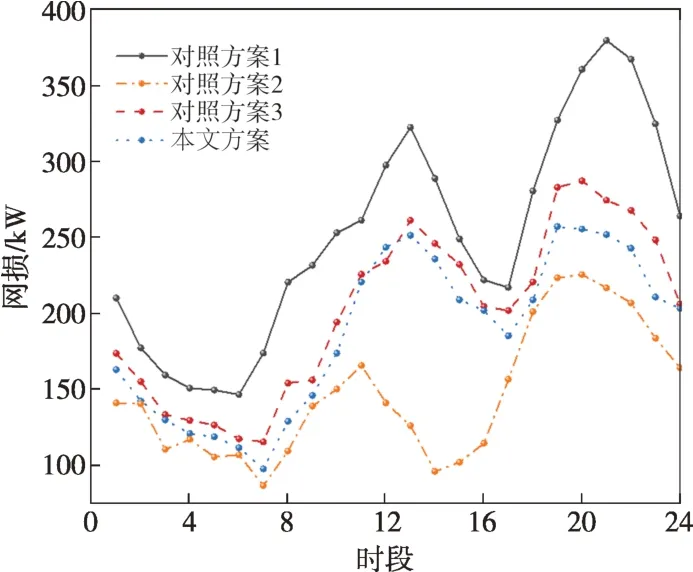
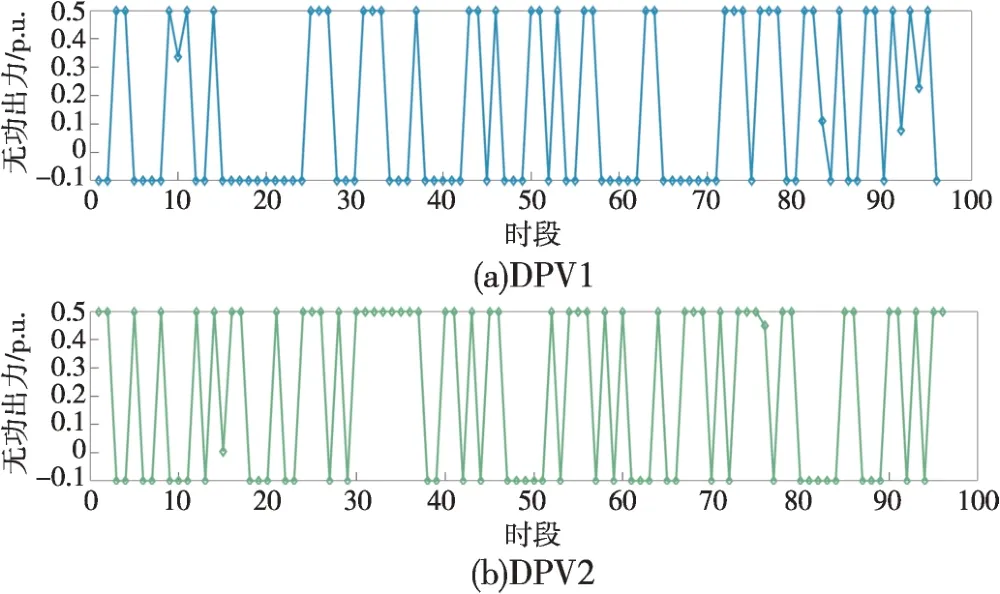
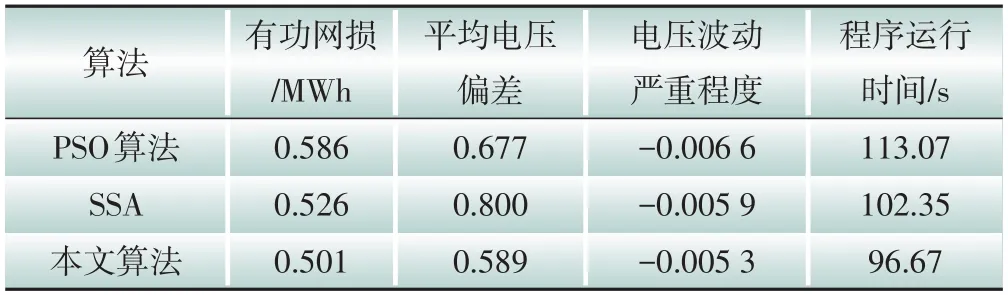
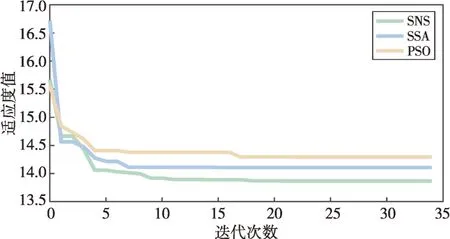
本地自适应电压控制曲线如图2所示,DPV逆变器控制流程如图3所示,其中:Ua和Ud分别为下垂控制的电压下限和上限,Ub和Uc分别为控制死区的下限和上限,Pmax和Qmax分别为有功、无功最大出力值,Uinew为有功出力削减过后的节点电压,Ustep为有功削减的步长电压。当Ua≤Ui≤Ud时,DPV以MPPT模式运行,具体无功出力情况如式(18)所示;当Ui>Ud或Ui 图2 本地自适应电压控制曲线Fig.2 Local adaptive voltage control curve 图3 DPV逆变器控制流程Fig.3 The DPV inverter control process 3.2.2 日内DPV优化模型 本文已在日前优化过程中得到了满足离散调控设备日内动作次数约束的离散调控变量24 h 动态最优档位序列,日内优化的主要目的是抑制由于出力、负荷预测的不确定性而导致的电压波动,使各节点电压尽可能接近日前优化值。因此,日内动态无功优化模型的目标函数为电压偏差,约束条件参考2.2节约束条件,即: 式中:f为日内优化函数。 采用改进后的IEEE 33 节点系统进行分析,拓扑结构如图4所示。基准电压为12.66 kV,在支路1-2接入调节范围0.9~1.1的OLTC,档位总数为9。将DPV安装在具有较大压降的节点(15和25)上以提高无功功率支持,DPV额定容量为1 MVA,DPV无功容量调节范围为-100~500 kvar。在节点18 和32 分别接入1 号和2 号电容器组(SCB1 和SCB),单组电容器为50 kvar,各节点分别安装10组和20 组。考虑设备使用寿命限制和动作经济成本,所有离散型调控变量的单日最大投切次数限值均为5 次[25],电压限值均为0.93~1.07 p.u.;各节点日前负荷预测值由IEEE 33 节点系统各节点负荷数据乘以该节点的负荷变化系数得到,考虑实际情况,日内实际值由日前值模拟随机误差得到;DPV出力采用某地典型的DPV出力数据。以1 h为一个时段,日前DPV出力预测数据与实际数据对比如图5所示,负荷预测数据与实际数据对比如图6所示,负荷变化系数如图7所示。 图4 改进IEEE 33节点系统拓扑结构Fig.4 Topology of the IEEE 33-node system 图5 DPV出力预测数据与实际数据对比Fig.5 Comparison of the predicted DPV data and the actual data 图6 负荷预测数据与实际数据对比Fig.6 Comparison of the predicted load data and the actual data 图7 负荷变化系数Fig.7 Load fluctuation coefficients 本文在求解优化问题时采用SNS 算法,这是一种在2021年由SIAMAK、HADI、MEYSAM等人[26]提出的元启发式算法。SNS 算法在种群更新过程中模拟社交网络中用户通过表达意见的情绪来获得更多人气的尝试,选择寻优更新路径,这些情绪被命名为模仿、对话、争议和创新。在迭代过程中,SNS 算法随机选择一种模式进行寻优,与常见的PSO(粒子群优化)算法和GA(遗传算法)相比,在局部搜索过程中拥有多种寻优机制的SNS 算法更不易陷入局部最优解。SNS 算法是一种无参数元启发式算法,独立于搜索空间的特性来解决问题,而常见的PSO 算法和GA 则需根据搜索空间的特性来调整参数。 采用本文所提方法对改进后的IEEE 33 节点系统进行日前无功优化,结果如表1所示。日前优化得到OLTC、SCB1、SCB2 静态最优档位序列是考虑ADN经济性、安全性情况下的最优解,但不满足离散设备日内最大动作次数约束。从表1可以看出虽然清晨、半夜时段DPV 有功出力为0,但是由于负荷较大,实际DPV逆变器无功出力仍然较大。 表1日前无功优化结果Table 1 The day-ahead reactive power optimization results 各节点电压波动程度如图8所示,在负荷较小且DPV出力较大的上午时间段,馈线末端的节点电压不稳定程度较严重,但是在离散设备与DPV的配合下没有出现电压越限情况。 图8 电压不稳定性指标Fig.8 Voltage instability indicators 本文通过谱聚类得到满足离散设备日内动作约束的OLTC、SCB1、SCB2动态最优档位序列,然后基于DPV出力、负荷需求的实际值和离散设备动态最优档位序列进行日内实时自治控制。为了验证本文策略的有效性,设置3 组对照试验方案:方案1,未进行无功调控的配电网状态;方案2,仅采用本文日前动态优化方法未进行日内优化,即忽略离散调控设备动作次数约束的最优解;方案3,采用文献[27]中的“预动作表”方法进行动态优化。 为了进一步衡量各方案中离散设备动作变化的区别,参考文献[19]的方法引入偏差均方值指标,其计算公式为: 式中:G′i,t为离散调控设备i在t时段的档位;Gi,t为离散调控设备i在t时段的最优档位值;Mi为离散调控设备i全天补偿偏差均值。 各方案离散设备档位如图9—11所示,不同方案优化结果如表2所示。 表2 不同方案的优化结果Table 2 Optimization results of different schemes 图9 OLTC不同方案调控策略Fig.9 OLTC control strategies under different schemes 图10 SCB1不同方案调控策略Fig.10 SCB1 control strategies under different schemes 图11 SCB2不同方案调控策略Fig.11 SCB2 control strategies under different schemes 方案2 中OLTC、SCB1、SCB2 的动作次数分别为22、18、19,无法满足离散设备的日内动作次数约束,不具备可行性。方案3与本文方案将各调控设备的调控次数减少至5 次,减少幅度为74.6%,均满足离散设备日内动作次数限值。本文方案中各离散设备偏差均方值明显低于方案3,说明本文所提策略通过谱聚类法的时序合并能使聚类前后差值最小,得到的离散设备动态最优序列更接近于离散设备静态最优序列。本文方案电压偏差高于方案2,但与方案1 和方案3 相比分别降低了28%和14.2%,说明本文方案可以有效改善ADN的电压状态。 选择日前优化中电压不稳定性最严重的节点17 的全天电压和ADN 全天网损进行进一步分析,结果如图12和图13所示。 图12 节点17全天电压Fig.12 Voltages at node 17 throughout the day 图13 ADN全天网损Fig.13 Network loss of ADN throughout the day 由图12 可以看出:方案1 中17 节点电压全天越下限且情况严重;方案2中电压仅在22:00时出现越下限趋势并被成功抑制,全天电压波动情况较小,电压稳定分布在0.95~1.05 p.u.,明显优于限值;方案3 较方案1 整体抬升了全天电压水平,但从20:00 至次日01:00 电压波动一直十分明显,全天电压波动情况较严重;本文方案整体电压波动趋势接近方案2,由于考虑了DPV 出力的波动及离散调控设备的动作次数约束,全天电压波动较方案2 稍高,但与方案1 和方案3 相比分别减小85.2%和63.8%,电压质量提升明显。 由图13 可以看出:在中午光照强度大、负荷需求小的时段,DPV 调控能力较弱,本文方案线损较方案2 升高明显,优于方案1,和方案3 基本相同。但在其余时段,本文方案线路网损与方案1和方案3相比分别减少了21.2%和13.6%。以15 min为一个时段,本文策略下的DPV逆变器无功出力如图14所示。 图14 DPV逆变器日内无功出力Fig.14 Intra-day reactive power output of the DPV inverter 为验证SNS算法求解无功优化模型的优越性,分别采用SSA(麻雀搜索算法)算法、PSO 粒子群优化算法、SNS 算法分别求解上述日前无功优化模型,SSA 和PSO 算法参数见文献[28-29]。优化结果如表3所示,各算法迭代曲线如图15所示。 表3 不同方案的优化结果Table 3 Optimization results of different schemes 图15 迭代曲线Fig.15 The iterative curves 由表3 可知:与PSO 算法相比,SNS 算法的网损减少14.5%,平均电压偏差减小12.9%,运行时间减少14.5%;与SSA 相比,SNS 算法的网损减少4.7%、平均电压偏差减小24.4%,运行时间减少5.5%。由图15可知,SNS算法的迭代速度最快、适应度值更加精准。综上所述,SNS 算法求解无功优化问题时具备一定优势。 本文建立了基于谱聚类的ADN动态无功优化模型,并采用SNS 算法求解优化问题,并在改进后的IEEE 33 节点系统进行了仿真验证。得出结论如下: 1)采用谱聚类算法确定OLTC 抽头位置和SCB 的日内动作安排,在满足最大动作次数约束的前提下,可以有效减少动态无功优化问题的求解维度,与其他聚类方法相比,离散设备偏差均值更小,优化效果更好。 2)与其他策略相比,本文优化策略有效平抑了电压波动,减小了配电网网损。SNS 算法多种进化机制的寻优效果明显好于GA 和PSO 算法,证明了SNS算法求解ADN动态无功优化这一混合整数、非凸、非线性优化问题的有效性。 本文仅考虑了DPV与传统离散调控设备进行协调控制策略,优化效果虽然明显,但在午时光伏大发、负荷较小且缺乏其他调控手段的情况下,抑制电压波动的效果有待提高。下一阶段研究将重点考虑双馈异步风力发电机、静止无功补偿器、小型燃气轮机及柔性负荷同时接入ADN的协调控制策略。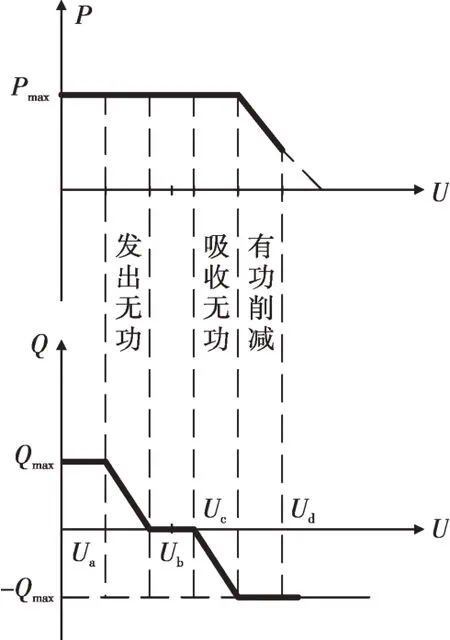

4 算例分析
4.1 算例基础数据
4.2 日前优化结果分析
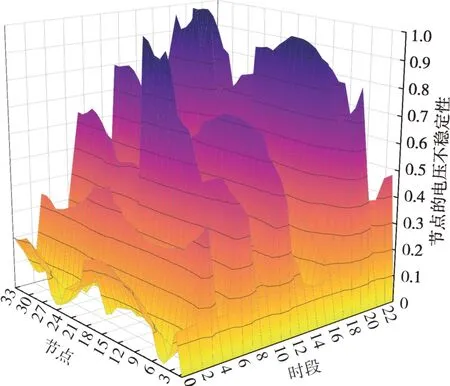
4.3 日内优化结果分析

4.4 算法有效性分析
5 结论

