基于ADMM的多区域直流系统完全分布式最优潮流算法

叶清泉，吴明启，吴旭光，陈 伟，高天乐，项 基

（1.国网浙江省电力有限公司平阳县供电公司，浙江 温州 325400；2.浙江大学 工程师学院，杭州 310015；3.平阳县昌泰电力实业有限公司，浙江 温州 325400；4.浙江大学 电气工程学院，杭州 310027）

0 引言

构建以新能源为主体的新型电力系统，是我国实现碳达峰、碳中和目标的关键途径［1］。将新能源发电单元作为分布式电源接入电网，有利于新能源的就地消纳，方便灵活且节约土地资源［2-4］。不同于交流电网，直流电网不存在无功补偿、频率同步等问题，供电可靠性与可控性较好，此外还减少了大量的电能变换环节，系统效率更高，因而较为适合分布式电源大量接入的场景［5-8］。现今，关于直流系统的优化和控制受到愈发广泛的关注。

最优潮流自20世纪60年代被提出以来，一直是电力系统领域的热门研究方向之一［9-10］。最优潮流指在满足系统稳定运行和安全约束的前提下控制与调节电力系统中的可控资源，以使系统运行于预期目标最优的工作状态［11］。接入分布式电源的直流电网具有大量可控资源，建立准确的直流系统最优潮流模型，并对其进行高效求解，对于电力系统的可靠经济运行具有重要意义［12］。直流系统的最优潮流问题是非凸、非线性的优化问题［13］，目前已有较多文献对该问题进行研究。文献［14］采用梯度下降法求解最优潮流，能够获得问题的局部最优解。文献［15］采用解析法推导直流网最优潮流问题的解析表达式。文献［16］利用遗传算法求解含有分布式能源的直流系统优化调度问题。文献［17-18］利用粒子群优化算法分别求解直流微电网和源网荷储互动的直流配电网优化调度问题。这类启发式算法能够获得优化问题的一个可行解，但该可行解与全局最优解的偏离程度难以被预计，同时求解较为耗时。文献［19］将交流辐射状网络的最优潮流问题松弛为二阶锥规划问题，并证明了在一定条件下松弛后的凸优化问题的解即为原问题的全局最优解，而凸优化问题的解则能够利用CPLEX、Mosek等求解器快速求出。

上述潮流优化方法均为集中式方法，需要由调度中心收集系统信息，经过集中计算后再下发控制指令。考虑到新型电力系统的可控资源较多，调度中心的计算量和存储量将会十分庞大［20］，并且调度中心保持和大量受控单元的可靠通信存在困难，电力系统的中控单元亦容易成为网络和物理攻击的目标［21］。此外，电力系统的不同区域可能会归属于不同的利益主体，集中式的优化方案需要统一收集各区域的信息，在隐私性上有所欠缺。分布式的优化方法将原问题拆分为多个更低维度的子问题进行求解，能够有效克服集中式优化方法的计算与通信瓶颈，保护隐私，对新型电力系统的特点具有较好的适应性［22］。

基于此，各类分布式潮流优化方法应运而生［23-26］。文献［27］将拉格朗日松弛方法应用于电力系统的多区域分布式发电调度中，但算法的迭代过程需要中央协调单元更新并向各区域分发拉格朗日乘子的数值，并非完全分布式的方法。文献［28］基于辅助问题原理构造了分布式的电压优化方法，但需要在所有区域之间交换节点信息。文献［29］提出了基于一致性理论的直流系统分布式成本优化方法，但并未将电力系统的潮流方程刻画进模型中。文献［30］采用ADMM（交替方向乘子法）构建直流配电网分布式最优潮流方法，然而所提方法仅适用于辐射状电力系统。文献［31］将ADMM应用于含风电场系统的线性直流最优潮流的分布式计算中，算法迭代过程中各区域接收相邻区域传递的边界节点信息，并在本区域中更新全局变量；但线性近似的模型有一定误差，难以得到最优潮流问题的最优解。

考虑到上述研究的不足，本文提出一种直流系统最优潮流的完全分布式算法。该算法基于直流系统最优潮流的二阶锥规划模型，能够求得辐射式网络以及环网最优潮流问题的全局最优解。算法的执行过程中首先由各子区域并行求解区域内部的最优潮流问题，再由相邻区域间交换边界断点信息，在区域内部更新对偶变量，迭代执行上述步骤以得到最优解。相较于已有的分布式算法，该算法无需中央协调单元处理拉格朗日乘子信息或协同各区域的边界一致性信息，因而属于完全分布式算法。

本文首先建立直流系统的最优潮流模型，对其应用二阶锥松弛方法得到直流系统的二阶锥最优潮流模型，然后在该模型的基础上构建基于ADMM的最优潮流分布式算法，再通过去除相邻区域边界节点相关联的一致性变量，将该算法改进成为完全分布式方法，最后在改进的IEEE 13节点和118节点直流系统上对算法进行测试。

1 直流系统最优潮流模型

直流系统可用有向图G=（N，E）表示，其中N为系统中母线构成的集合，E为系统中线路构成的集合，i-j∈E表示系统中首端节点为i，末端节点为j的线路。直流系统线路模型如图1所示，其中：Ui为节点i电压；pi为节点i的净注入有功功率，为节点所接发电机发出功率pgen，i减去负荷消耗功率pload，i；Rij为线路ij电阻，Iij为线路ij电流，Pij为线路ij首端功率。

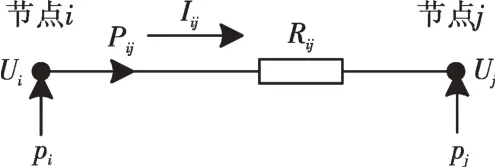
图1 线路模型Fig.1 Schematic diagram of the line model

直流系统最优潮流问题是一个数学优化问题，由目标函数与约束条件构成。

1.1 目标函数

直流系统最优潮流问题中两类常见的目标函数分别为：

1）最小化系统网损：

2）最小化发电成本：

式中：c0，i、c1，i、c2，i均为非负常数，取决于相应分布式电源的发电特性。当c2，i=c0，i=0 且c1，i=1 时，式（2）与式（1）相同。

1.2 约束条件

直流系统最优潮流问题的约束条件涉及潮流方程约束以及电网的安全运行约束。其中潮流方程约束由以下4个等式构成：

式（3）为节点的净注入功率表达式；式（4）为欧姆定律表达式，表征线路电流与其两端节点电压的关系；式（5）为节点功率平衡表达式，表征流入节点功率与流出节点功率大小相等；式（6）为支路首端功率定义式，为支路首端节点电压与支路电流的乘积。

电网的安全运行约束包含3个不等式约束，分别为节点电压上下限约束、线路传输功率约束以及电源出力约束：

式中：上标u和l分别表示相应变量的上界和下界。通常平衡节点处电压标幺值固定为1，其余节点电压偏差限制在基准电压值的5%以内。

1.3 最优潮流模型

根据上述目标函数和约束条件，直流系统的最优潮流模型表示如下：

式中：pgen为分布式电源的有功出力，是控制变量；U、I、p、P分别为节点电压、支路电流、节点净注入功率、支路首端功率，是状态变量。pgen、U、I、p、P共同构成最优潮流模型中的优化变量。

2 最优潮流的二阶锥规划模型

非线性等式约束式（6）的存在使得直流系统最优潮流模型是非凸优化模型，不便于求解。本节利用二阶锥松弛方法，将非线性约束松弛成为二阶锥约束，从而将模型转化为二阶锥规划模型。

首先引入节点i电压平方变量ui和线路ij电流平方变量lij，将式（6）左右两边同时平方后可得：

再将其松弛为不等式约束：

式（11）可写为二阶锥约束的标准形式，即：

利用二阶锥约束式（12）替换非线性等式约束式（6），得到转化后的最优潮流模型，若转化后模型的最优解能够使得式（12）取得等号，则称该二阶锥松弛为精确松弛，此时二阶锥模型的最优解即为原最优潮流模型的最优解。当系统中各节点具有相同的电压上界约束并且节点功率的下界为负值，或者各节点无电压上界约束时，二阶锥松弛能够保证为精确松弛［32］。针对其他情况，可通过仿真验证式（12）中的等号是否成立，从而测试该种情况下二阶锥松弛的精确性。

相应地，对于欧姆定律约束式（4），利用电压平方变量与电流平方变量替换其中的电压变量和电流变量，可得：

对节点功率平衡表达式（5）和节点电压上下限约束式（7）进行同样的变量替换操作，可得：

综上，可建立直流系统最优潮流的二阶锥规划模型如下：

该二阶锥规划模型是典型的凸优化模型，因而能够方便地求得该模型的最优解，后文将基于该模型建立直流系统最优潮流的分布式算法。

3 最优潮流的完全分布式算法

本章首先对ADMM进行简单介绍，再通过断开相邻区域边界节点的方式进行网络拆分，从而得到解耦后的最优潮流模型，基于解耦后的模型推导直流系统最优潮流的分布式计算方法，再去除其中的一致性变量以将其改进为完全分布式算法。

3.1 ADMM

ADMM是一种分布式优化方法，它将原问题分解成为若干个子问题，再协调各子问题的最优解以获得原问题的最优解。当原问题为凸优化问题时，ADMM可以收敛到该问题的全局最优解。

ADMM 适用于求解变量可分离的优化问题，如：

式中：x和z为优化变量，目标函数f(x)和g(z)均为凸函数，约束条件为线性等式约束；A和B为优化变量x和z的系数矩阵，c为等式约束等号右侧向量，它们均为常量。

上述优化问题的增广拉格朗日函数为：

式中：ρ为罚参数；y为对偶变量。

ADMM 的执行过程为：首先依次完成变量x和变量z的更新，即求解两个子优化问题，利用求解结果更新对偶变量y，再将新的对偶变量值代入子问题中重新求解，不断重复上述过程直至满足设定的迭代终止条件。

算法的数学表达式如下：

式中：上标k表示当前迭代次数，下同。

通过定义新的对偶变量vk=yk/ρ，ADMM 的执行步骤可以简化为：

在算法迭代过程中，用原始残差rk反映第k次迭代解的原始可行性，即式（18）中等式约束的满足情况，用对偶残差dk反映第k次迭代解的对偶可行性，即所得解与问题最优解的偏差，原始残差rk和对偶残差dk分别为［33］：

随着迭代进行，残差将逐渐减小直至满足设定的终止条件，算法终止条件可以写为：

式中：ε为设定的最大允许误差。

3.2 直流系统最优潮流的分布式算法

直流系统的二阶锥最优潮流模型式（17）并非变量可分离的优化模型，因而不能直接应用ADMM分布式求解。本文考虑将原始网络拆分为多个子区域，构造各区域变量解耦的最优潮流模型，以便应用分布式算法求解。

3.2.1 区域拆分方式

本文通过断开相邻区域边界节点的方式进行区域拆分。对于边界断点的设定以及区域拆分方案具有如下规则：

1）在断开所设定的边界断点后，原始网络可被拆分为若干个彼此之间不联通的子区域。

2）规定每个断点负责沟通两个相邻区域，因而断点将被复制到两个区域中，并且在两区域中被分别称为原始节点和分裂节点，至于在哪一区域中被称为原始或分裂节点可以任意选择。

3）若某条支路的两端均设定了断点，则该支路可以保留在两相邻区域中的任一区域。

图2所示为一个5节点网络的拆分示意图，通过断开节点1与节点3可将原始网络拆分为2个子区域，其中断点1在子区域1中称为原始节点（1，1），在子区域2 中称为分裂节点（2，1′），断点3 在子区域1 中称为分裂节点（1，3′），在子区域2 中则称为原始节点（2，3），线路1-3保留于区域1中。显然，线路1-3亦可以保留于区域2中，分裂节点与原始节点在不同区域中也可以交换的，例如可将断点1在子区域1 中标注为分裂节点（1，1′），在子区域2中标注为原始节点（2，1）。

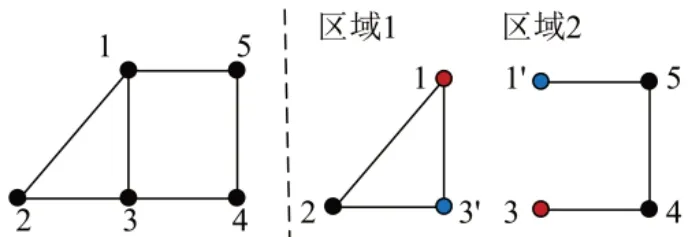
图2 5节点网络的拆分示意图Fig.2 Schematic diagram of a split 5-bus network

3.2.2 区域解耦最优潮流模型

假设原始网络被拆分为H个子区域，对区域{a|a=1，2，…，H}定义本地变量xa，由子区域的二阶锥最优潮流模型中的全部变量组成。定义描述节点信息的局部变量为xa，i=[ua，ipa，i]T，描述断点信息的全局变量为：

式中：D为断点集合。每个断点都被拆分，形成区域a内的原始节点集合ai和相邻区域a′内的分裂节点集合a′i′。此外，用aj′表示相邻区域a′中的原始节点集合，aj′表示区域a中的分裂节点集合。

显然，原始节点和与之对应的分裂节点的节点电压平方值相同，节点注入功率之和为断点i处的负荷功率，即有如下关系：

式（30）可概括为：

式中：Ci为等式约束等号右侧向量。式（31）反映了相邻区域之间的耦合关系。为了实现子区域之间的解耦，引入全局变量zi，将等式约束改写为：

再将其分别归属于区域a和区域a′中，此时，在每个子区域中将仅存在本地变量xa和全局变量z，而不再包含其他区域的局部变量，全局变量保证断点对应变量在不同区域中具有一致性，因而亦称为一致性变量。假设子区域a中存在原始节点ai和分裂节点aj′，则有：

原始网络的最优潮流模型转化为：

式中：fa(xa)为优化模型式（17）中区域a最优潮流问题的目标函数；ga(xa)≤0和ha(xa)=0分别为区域a最优潮流问题中的不等式约束和等式约束。由于额外添加的两个边界条件约束均为线性等式约束，不影响问题的凸性，因此利用ADMM对该模型求解能够保证算法的收敛性。

3.2.3 最优潮流的分布式算法

对解耦后的最优潮流模型应用ADMM建立最优潮流问题的分布式算法。首先写出优化问题式（34）所对应的增广拉格朗日函数为：

式中：va，i和va，j′为对偶变量；Xa为满足ga(xa)≤0和ha(xa)=0的关于xa的凸集合。

直流系统最优潮流的分布式算法的步骤为：

考虑到增广拉格朗日函数对各个子区域的可分解性，即：

式（36）可以表示为：

3.3 最优潮流的完全分布式算法

上述算法执行过程中需要中央协调单元完成全局变量的更新，本文考虑消除其中的全局变量及其更新步骤，从而去除用以处理断点处一致性信息的中央协调单元，建立完全分布式的算法。

首先根据式（37）可以写出更新全局变量的解析表达式为：

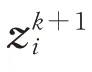
比较式（42）和式（44），可得：

因此zi的更新可简化为：

将式（46）代入式（38）和式（39），可得对偶变量的更新表达式为：

为使表达更加简洁，引入辅助变量以替换原对偶变量，辅助变量定义如下：

对于式（47）和式（48），用式（46）替代zi，用式（49）替代va，i，用式（50）替代va′，i′。经过上述处理，可写出改进后的直流系统最优潮流的分布式算法步骤如下：

本地变量xa的更新式（51）类似于子区域最优潮流问题的求解，仅是在目标函数中增加了二次惩罚项。式（52）和式（53）为区域a内对偶变量的更新。在改进后的算法中相邻区域之间交换断点处信息以更新区域内的对偶变量，不再需要中央协调单元与所有区域进行通信以处理断点处的一致性信息。图3展示了算法执行时两子区域间的信息交换情形。

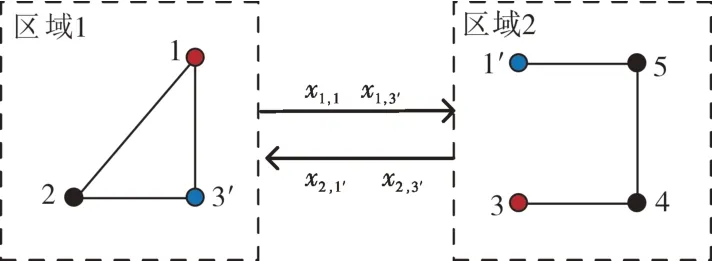
图3 两区域间的信息交换情形Fig.3 Information exchange between two regions

根据ADMM 中原始残差式（26）与对偶残差式（27）的定义，可得最优潮流完全分布式算法的原始残差与对偶残差。定义算法在第k次迭代后的原始残差列向量rk为：

即将所有子区域内各断点处的原始残差排列为一个列向量。同理，将对偶残差排列为一个列向量可形成对偶残差列向量dk为：

当rk以及dk中各项均小于设定的最大允许残差时迭代终止，即需要使得式（56）成立：

式中：sk为边界残差。

算法的具体流程如图4所示。

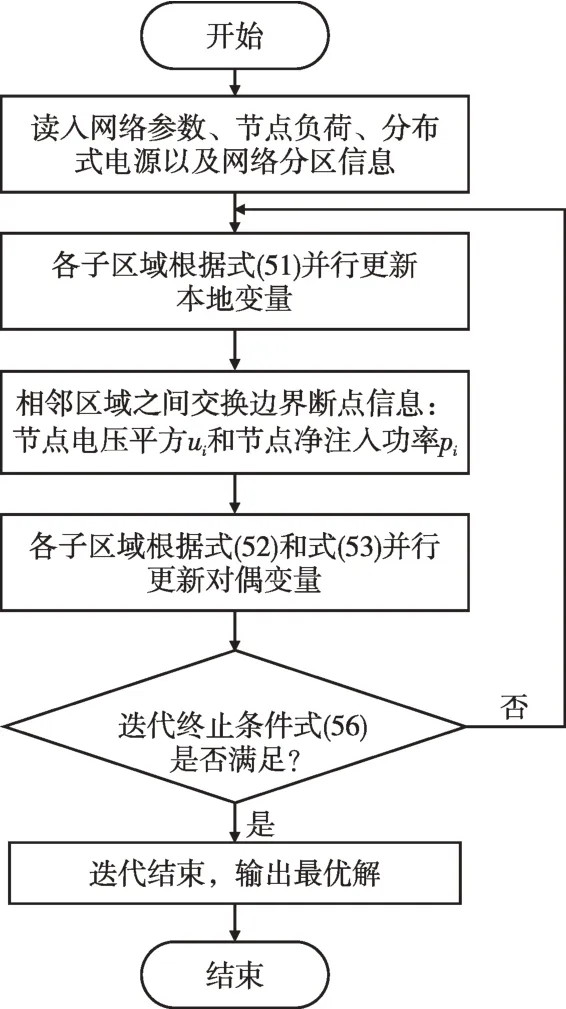
图4 最优潮流完全分布式算法的流程Fig.4 Flow chart of the fully distributed OPF algorithm

4 算例分析

本文忽略IEEE 13节点和118节点系统算例中的线路电抗及无功潮流成分，从而构建出直流系统算例，对最优潮流完全分布式算法进行仿真测试。13 节点和118 节点系统算例的网络结构及复杂程度、负荷大小、电源容量及接入位置等均具较大差异，便于测试算法应用于不同系统时的准确性与收敛性。最优潮流计算程序基于Julia 编程语言以及JuMP 建模工具包开发，测试在CPU 为AMD R3550H、内存为16 GB 的计算机上进行，采用Mosek 9.3 求解器进行每个子区域的优化求解。

仿真测试中用到的13 节点直流系统的拓扑结构如图5所示，该系统包含有16条支路、4组分布式电源，分别位于节点1、8、11、13 处，将2、4、5、6、10号节点作为断点从而将网络拆分为两个子区域。图6为仿真中用到的118节点直流系统拓扑，该系统包含有170 条支路、19 台分布式电源，分别位于节点10、12、25、26、31、46、47、49、54、59、61、65、66、80、87、89、100、103、111 处，将网络从节点70、69、33 处断开，拆分为3个子区域。两个算例均选择额定电压为基准电压、100 MW为基准功率，仿真基于标幺值进行。此外，将13 节点系统中各分布式电源出力上界均设置为5 MW，118节点系统中分布式电源出力上界数据见表1，两系统中分布式电源出力下界均设置为0，网络参数、节点负荷等信息参见文献［34］，仿真中选择最小化系统网损为优化目标。

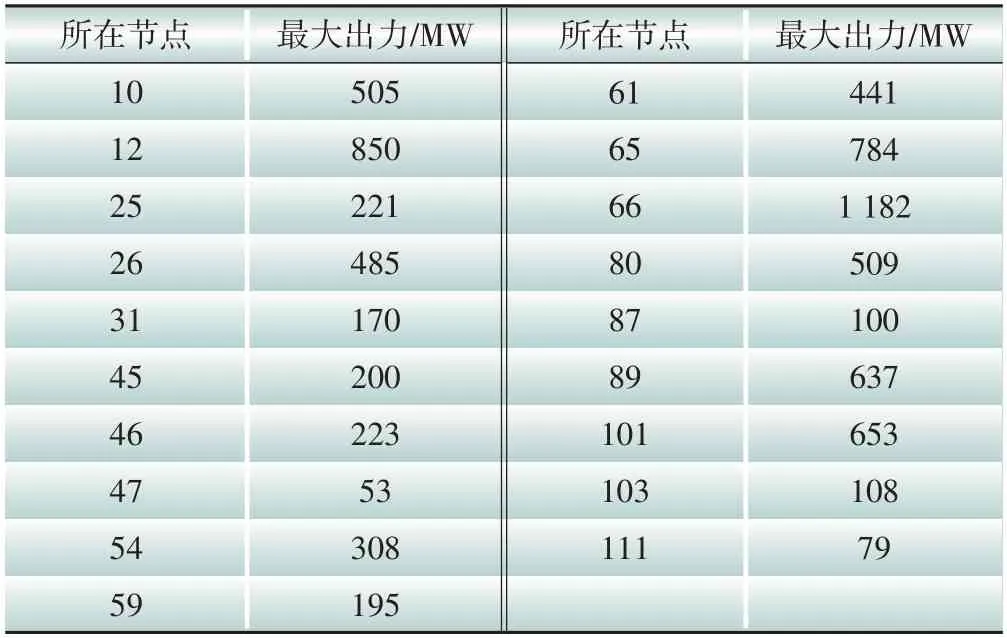
表1 改进的IEEE 118节点系统中分布式电源的最大出力Table 1 The maximum output of distributed generation in the modified IEEE 118-bus system

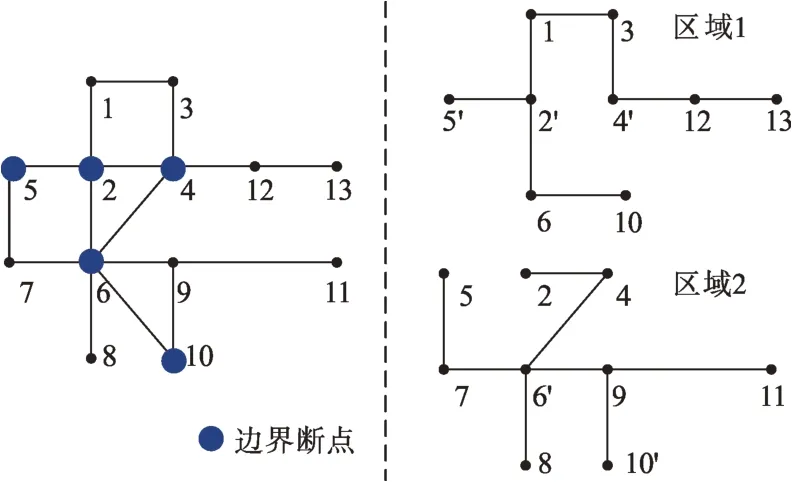
图5 改进的IEEE 13节点系统拓扑Fig.5 Topology of the modified IEEE 13-bus system

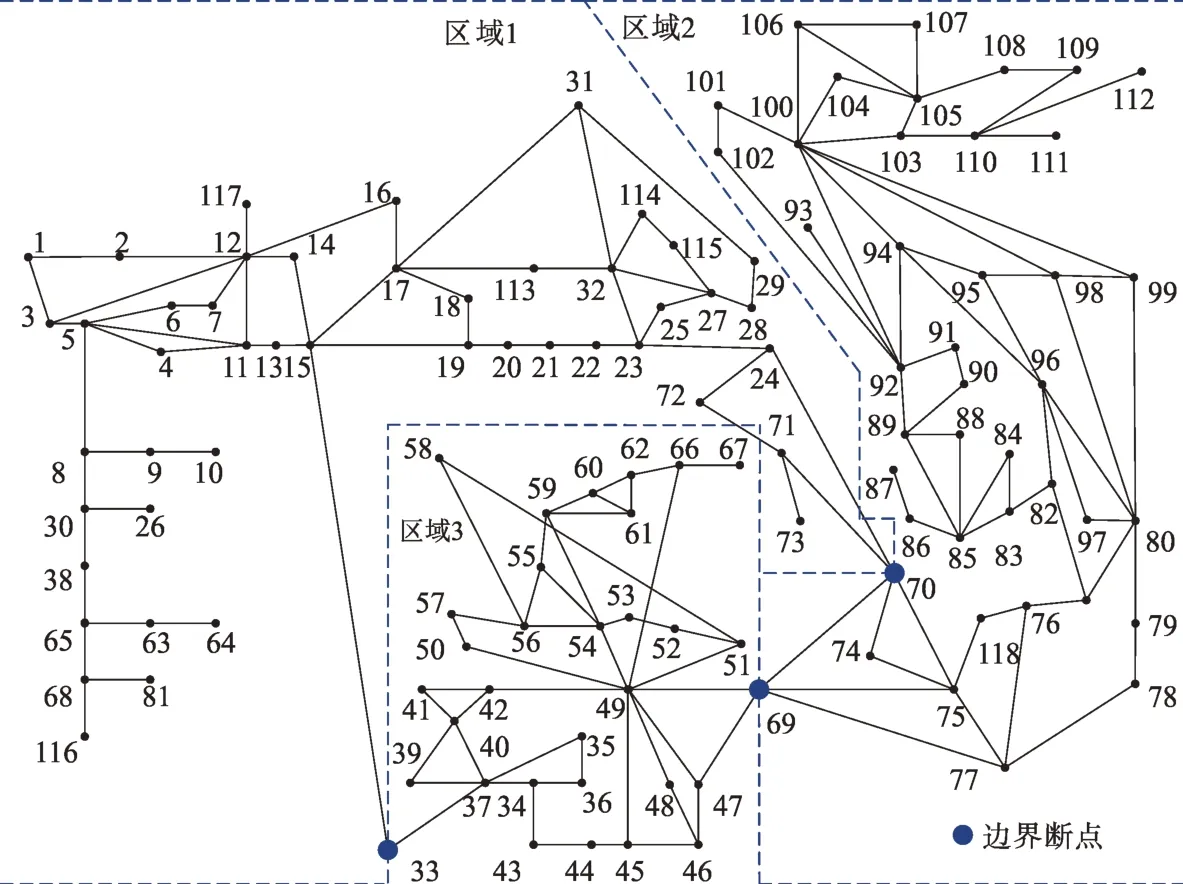
图6 改进的IEEE 118节点系统拓扑Fig.6 Topology of the modified IEEE 118-bus system

本章首先利用13 节点系统测试分布式算法能否收敛以及迭代结束后边界处断点相关信息在不同区域中的一致性，再利用118节点系统分别从算法收敛性、计算结果的松弛精确性、算法对罚参数选择的敏感性以及对子区域个数的敏感性4个角度测试并分析分布式算法的性能。

4.1 13节点算例边界一致性分析

利用分布式算法计算13 节点直流环网系统最优潮流，边界断点对应两相邻区域中的原始节点和分裂节点，仿真结果如表2所示。

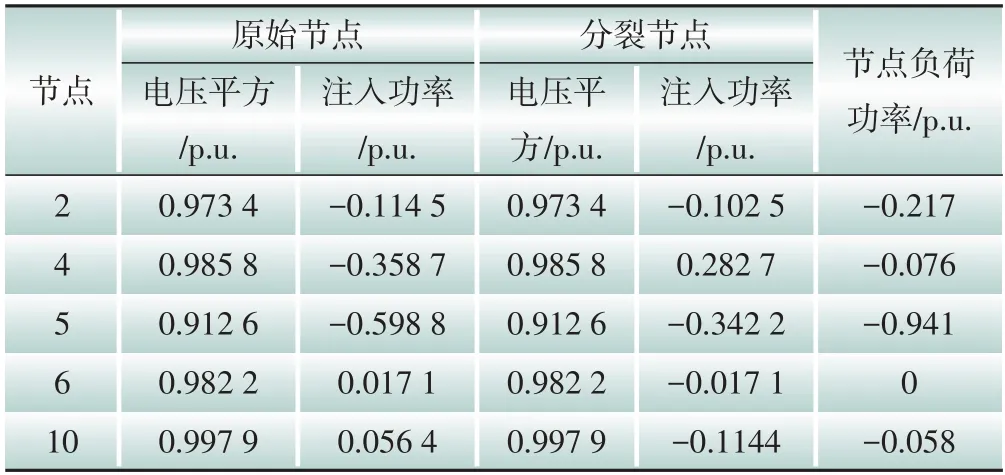
表2 原始节点与分裂节点变量比较Table 2 Comparison of variables at original nodes and split nodes

由仿真结果可知，各断点在相邻区域中的节点电压相同，节点注入功率之和等于节点处的负荷功率，因此对于该13 节点系统，迭代收敛后边界节点在不同区域中可保证一致性，能够较好满足一致性约束（即式（32）），后文将基于118节点网络对算法进行进一步的验证与分析。

4.2 算法收敛性分析

利用分布式算法求解118 节点系统的最优潮流，图7为算法迭代过程中计算出的各台分布式电源出力的变化情况，右侧图例表示分布式电源所处节点，如“10”表示接于10 号节点处的分布式电源。图8中的实线为算法迭代过程中网络有功功率损耗的变化曲线，虚线为利用集中式算法即直接调用求解器求解式（17）得出的最小网损。可见分布式算法的最优解在20 次迭代内即能够收敛于稳定值，此时最优值收敛到与集中式算法一致的结果。

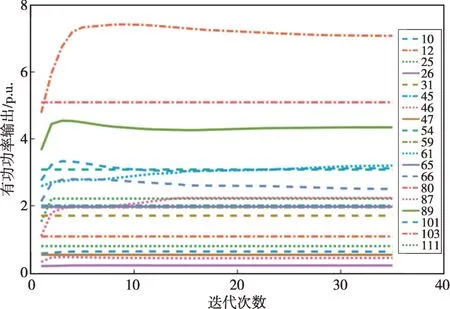
图7 分布式电源出力的收敛性Fig.7 Convergence of the output power of DGs

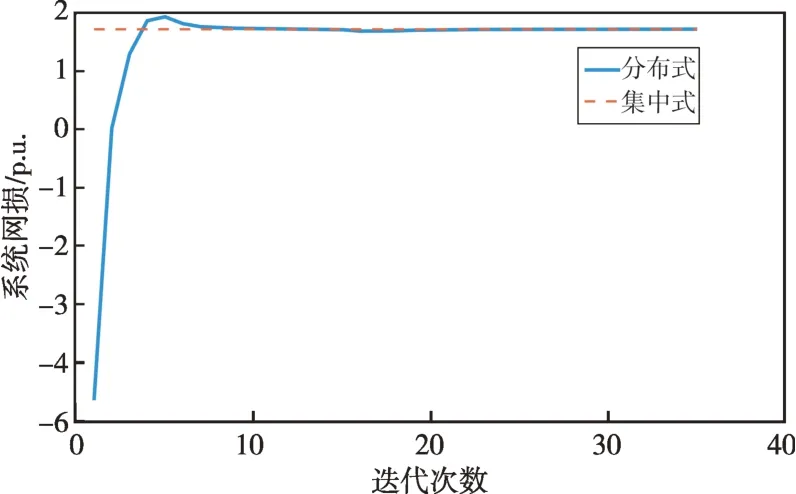
图8 网络有功功率损耗的收敛性Fig.8 Convergence of the active power losses

4.3 松弛精确性分析

为刻画二阶锥松弛的精确性，定义各条支路的松弛偏差为：

考虑到计算机的数值计算误差，若松弛偏差能够充分接近0，则可以认为在该条支路上二阶锥松弛是紧的。利用分布式算法求解118节点系统的最优潮流后，计算出各支路的松弛偏差如图9所示。由仿真结果可见系统所有支路的松弛偏差均小于0.15%，较为接近0，体现了二阶锥松弛的精确性，验证了第2章中的理论分析，表明该分布式算法能够计算出直流系统最优潮流的全局最优解。

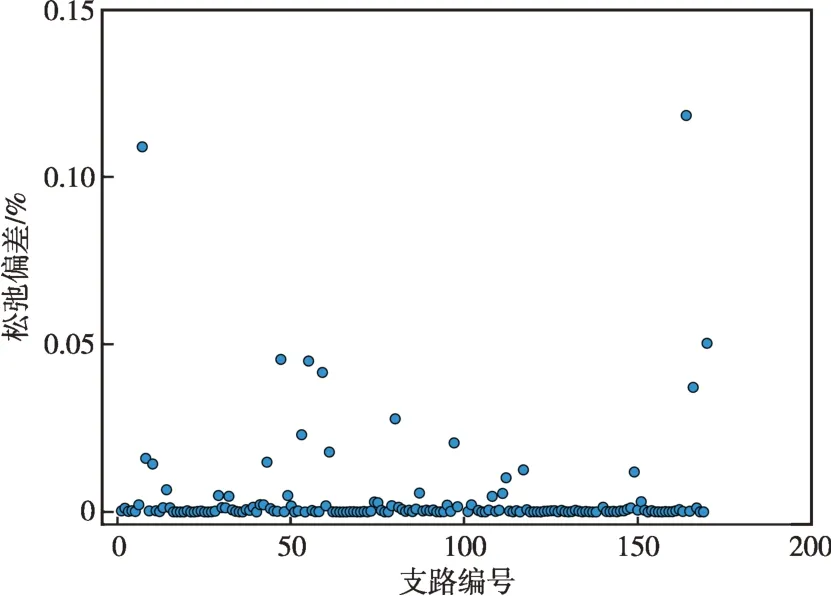
图9 直流系统二阶锥规划最优潮流模型的松弛偏差Fig.9 The relaxation variations of the second-order cone programming OPF model in DC power systems

4.4 算法对区域个数的敏感性分析

划分的区域个数会影响分布式算法的收敛性，为分析算法对子区域个数的敏感性，本文针对118节点系统增设了6区域的划分方案，与前文的3区域划分方案进行对比。网络被6 个断点8、33、49、69、70、100断开为6块子区域。图10所示为算法迭代过程中边界残差变化曲线，可见在迭代初期，对应于两种不同的区域划分方案，边界残差的下降速率较为接近，3区域场景算法经过75次迭代残差下降到10-3以内，6 区域场景算法则需89 次迭代。但若要实现更加小的边界残差，子区域多的场景需要更多次迭代，如若最大允许残差设置为10-4，则3区域场景算法需迭代110次，6区域场景算法需迭代265次。在实际应用中，最大允许边界残差可设定在10-3左右，从而在满足优化精度要求的同时减少迭代次数，缩短算法求解时间。

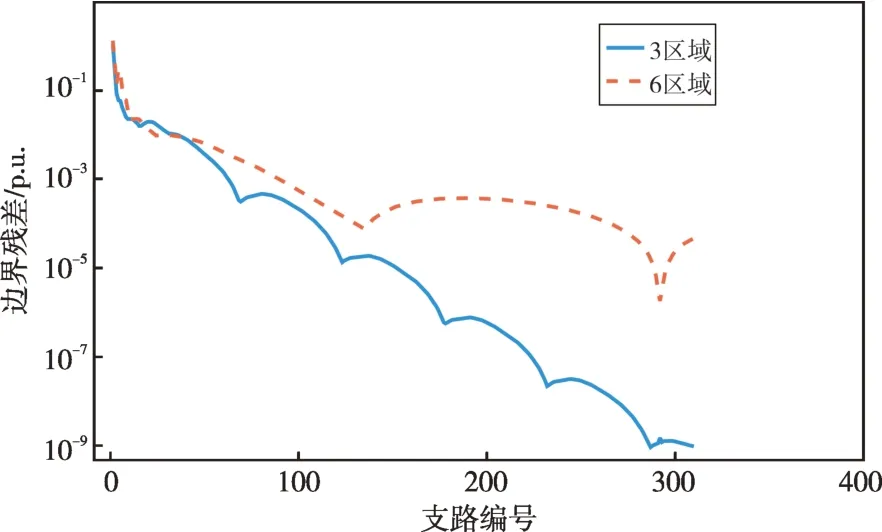
图10 分布式算法迭代过程中的边界残差Fig.10 Boundary residuals in the iterative process of the distributed algorithm

4.5 算法对罚参数值的敏感性分析

在执行分布式算法前需要确定罚参数的大小，罚参数值设置恰当与否会影响算法的收敛速度。本节测试分布式算法对罚参数值的敏感性，首先将罚参数分别设置为0.01、1、100，将迭代次数统一设置为200次，进行118节点系统最优潮流的仿真测试，仿真结果如表3所示。

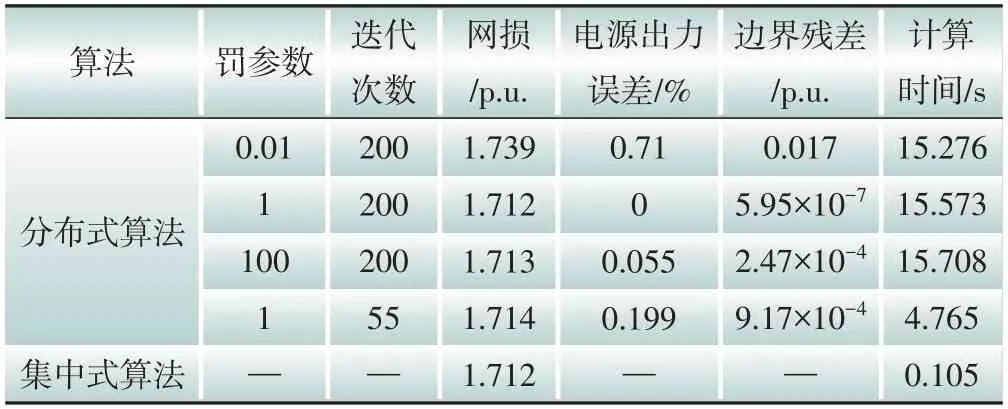
表3 对应不同罚参数的分布式算法求解结果比较Table 3 Comparison of solutions of distributed algorithm with different penalty parameters

表3中电源出力误差为分布式算法计算出的各台分布式电源出力和集中式算法计算结果的误差之和，计算公式为：

表3展示了罚参数值设置为1，最大允许边界残差设置为10-3时分布式算法的求解情况，可见算法仅需55 次迭代即可满足终止条件，计算时间为4.765 s。仿真过程中分布式算法各子区域的计算均是在一台计算机上进行，若在实际工程中应用该算法，对应于3个子区域应有3台分布式运算单元同时进行子区域的优化运算，若忽略子区域之间的通信延时，算法的执行时间应为1.6 s 左右。在计算精度方面，该参数设置下分布式算法得到的最优网损相较于集中式算法增加了0.12%。由表3可知，最大允许边界残差的值越小，则分布式算法的计算结果越接近集中式算法的结果，但相应的计算时间也会有所增加。

5 结语

本文提出了一种求解直流系统最优潮流的完全分布式算法，相较于已有算法，本算法的主要特征有：

1）算法执行时各子区域并行求解区域内部最优潮流问题，无需按照先后次序串行求解，减少了计算耗时。

2）各区域内的优化问题求解完成后，仅需在相邻区域间交换少量边界节点相关信息，减轻了通信负担，提高了私密性。

3）各区域利用接收到的信息完成区域内对偶变量的更新后，各变量的一次更新迭代过程完成，过程中无需中央协调单元采集、更新、分发边界节点相关的一致性变量信息。

4）分布式算法依托于直流系统的二阶锥最优潮流模型而建立，能够收敛到辐射式网以及环网拓扑直流系统最优潮流问题的全局最优解。

改进的IEEE 13节点和118节点系统验证了所提出的分布式算法的收敛性以及准确性。本文的不足之处在于仅考虑了单时段的潮流优化，未来将研究算法在多时段动态潮流优化下的表现，进一步提高算法的实用性。