基于Shapley值与全局和声搜索算法的电网投资组合策略
康 朋,孙安黎,唐立波,刘子毅,张金良
(1.国网重庆市电力公司经济技术研究院,重庆 400015;2.华北电力大学 经济与管理学院,北京 102206)
0 引言
随着国内经济的稳步增长,国家工业化、城镇化水平的不断提升,电力行业实现了高速发展。与此同时,电能替代深入广泛推进,终端用电容量持续攀升,社会对于电力的需求不断加大。据预测,全社会用电总量在“十四五”和“十五五”期间,分别以4.5%和3.5%的年均增速稳定上升,2030年将达到1.11×1013kWh。基于此,电网投资的力度也随之上升,而电网企业如何把有限的资金应用到提升电网经济性、可靠性的项目中,以落实好电网项目投资决策的工作是亟须思考的问题。投资决策是指投资主体在调查、分析、寻优的基础上,对投资活动所做出的最后决断。科学合理的投资决策可为电网企业提高资金利用效率提供有力保障。对于电网项目投资而言,投资决策方案的制定需要考虑企业的投资能力、电网的经济性等因素。因此,研究电网企业投资决策问题具有非常重要的现实意义。
对于电网投资组合优化研究,现有研究主要侧重于两个方面:一是针对投资组合优化模型设计的研究;二是针对模型求解计算方法的研究。在模型设计方面,文献[1]以智能电网业务投资为研究对象,基于最优综合效益,构建了多目标决策优化模型。文献[2]从经济、社会及电网安全的维度入手,根据最优投资效用设计目标函数,从而构建优化模型。文献[3]根据电网投资项目所带来的经济效益、社会影响与可靠程度,给出最优投资组合模型。为考虑不同地区实际的电力需求,文献[4]以经济效益最优为目标进行投资优化分析,在分析中加入了地区因素,从而实现投资效益最大化。文献[5]构建基于年预期最大收益的投资优化模型,算例结果验证了该模型可为企业合理安排项目投资提供有效支撑。文献[6]计及资金、项目等约束条件,同时考虑电网投资的经济性、可行性与发展性,构建多目标优化模型。
在对优化模型的求解研究方面,传统的方法包括动态规划法和整数规划法等,随着影响因素的增多和实际工程复杂程度的增强,传统方法求解的局限性逐步显现,为此,学者们逐渐将群智能体优化算法应用到优化模型的求解中。其中应用较为广泛的有蚁群算法[7]、粒子群算法[8-9]、布谷鸟算法[1-2]和遗传算法[10]等。文献[11]采用改进的蚁群算法对具有多目标的电网规划问题进行研究。文献[12]用改进的粒子群算法求解电网投资管控中包含的多目标优化问题。文献[13]在约束条件中考虑了投资能力,并采用随机权重布谷鸟算法求解所构建的投资组合优化模型。文献[14]应用非支配排序算法与遗传算法,并将两种算法的优势进行互补,对多目标电网规划进行研究。除上述群智能体优化算法外,合作博弈[15]和技术成熟度理论[16]等方法也被用于解决电网投资决策的问题中。然而,目前对于优化模型的求解方法仍存在求解速度慢、精度差等局限,和声搜索算法相较于其他早期的启发式优化算法能够更好地被各种类型的最优化问题所采用,且该算法具有较强的鲁棒性和通用性,涉及的参数较少。为此,本文提出采用改进的和声搜索算法对新型电力系统下电网项目投资组合策略进行优化。首先,基于Shapley值法构建目标函数。原因在于,各效益在总体效益中所占的比重是不同的,Shapley值法能够按照成员对联盟最终获益的贡献大小来决定每个成员的所得,体现了分配的合理性与公平性。故采用Shapley值法计算各效益函数的权重,并为不同效益函数赋权,最后建立总目标函数。该方法相比传统等权重直接加和构建目标函数的方式更贴近实际,为建立科学合理的目标函数奠定了基础。其次,为解决电网项目投资组合问题,构建以综合效益最优为目标的电网投资策略优化模型,并将改进的和声搜索算法应用于电网投资决策的模型求解中。最后,通过实例分析获取最优投资组合策略,并对所提模型与求解算法的价值进行验证,为企业投资电网项目提供决策支撑。
1 Shapley值法及思路
Shapley值法是Shapley 提出的一种处理各联盟成员参与总目标分配利益的方法,能够高效地解决各个参与者在合作中的贡献分摊问题,并达到了分摊结果更为公正的目的[17-18]。本文从电网企业以项目投资所获得的综合效益最优为目标,对项目投资策略进行制定。因此,明确构成总效益的各部分效益并对不同的效益组成部分进行分析是后续模型构建的基础。由于经济、社会、环境、安全4个维度产生的效益对电网投资综合效益产生了巨大影响,故将上述不同效益作为电网投资综合效益的关键组成部分。根据Shapley值在收益分配中的应用,可将各效益函数共同作用所产生的综合效益视为收益,根据各效益之间的关系,将综合效益分配在不同的效益函数中,即确定每种效益函数在总效益函数中所占的权重。不同效益函数对组合的贡献越大,最终分配的权重也就越大[19]。
Shapley值法计算权重的基本思路如下。
1)在Shapley值法中,各个效益函数的权重分配计算公式如下:
式中:p为效益函数集合中的任意子集;|p|为子集中效益函数的个数;ω(|p|)为加权系数,表示某个效益函数在综合效益中的权重;k为Shapley 组合中的某个效益函数;A(p)为子集p的效益;A(pk)表示在子集p中除去第k个效益指标后可取得的效益;Ak为效益函数k分配的误差量,即Shapley值;N为效益函数的总数。
2)根据上述公式,得到Shapley总效益函数中各个效益函数所占的权重ωj,计算公式如下:
式中:A为Shapley值的分摊总和。
2 基于综合效益最大化的电网投资组合决策模型
电网投资决策优化的目的是找到科学合理的电网投资策略使得企业的经济效益达到最优。同时,电网公司要承担社会责任,在保证自身经济利益的同时仍要兼顾环境效益。由于电网公司的重要职责是为用户输送电能,因此,电量、用户满意度等有关社会效益的因素是投资时需要考虑的。另外,高比例可再生能源广泛接入是新型电力系统的特征之一,风能与太阳能都伴随着不确定性和非连续性等特点,这会考验决策者如何进行电网投资以保证供电的可靠性。综上可知,经济效益、社会效益、环保效益以及安全效益在电网投资中需要着重考量[20]。其中,目标函数构建流程如图1所示。
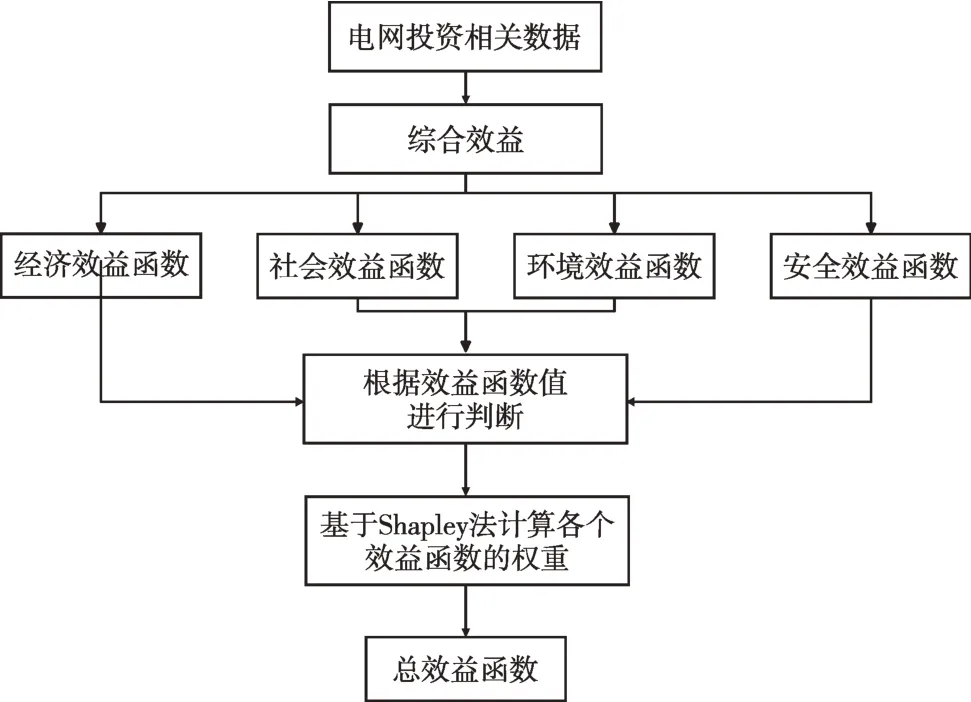
图1 目标函数构建流程Fig.1 Flow chart of objective function construction
2.1 目标函数
基于综合效益最优的准则,建立电网投资决策的目标函数,其中考虑了经济效益函数、社会效益函数、环保效益函数、安全效益函数及投资能力惩罚函数,见式(4)。
式中:ηi为电网项目i的投资决策变量,当ηi=1时,则投资项目i,当ηi=0 时,则不投资项目i;Btot(ηi)为总效益函数,通过计算可得到电网投资的综合效益;Beco(ηi)为经济效益函数;Bsoc(ηi)为社会效益函数;Benv(ηi)为环保效益函数;Bsec(ηi)为安全效益函数;Cpenalty(ηi)为投资能力惩罚函数;ω1、ω2、ω3、ω4分别对应经济效益函数、社会效益函数、环境效益函数和安全效益函数所占的权重。
2.1.1 经济效益函数
经济效益函数可考察电网企业投资某项目对电网盈利的影响,其为各项目的收益与成本之间的差值,具体如式(5)所示。
式中:Bi,t为第i个项目在第t年的收入;Ci,t为第i个项目在第t年所需要的运行成本;T为建设项目的寿命周期;n为电网项目总数;r为投资回报率,表示在投资活动中获得的经济回报;Ei为第i个项目的投资成本。
2.1.2 社会效益函数
除经济效益外,社会效益仍是电网企业投资决策时需要重点考虑的一部分。电网企业承担着为用户提供安全可靠用电服务的责任,因此,将停电成本作为评判投资项目产生社会效益的关键指标。社会效益函数见式(6)。
式中:vi,t为第i个项目在第t年的新增装机容量;v为原有电网能够承载的最大负荷量;pimax为第i个项目因停电而耗费的最高成本。
2.1.3 环保效益函数
传统的火电导致大量的空气污染物排放。利用风、光等绿色能源发电可有效减少大气中的污染物,在实现清洁发电的同时也促进了新能源的消纳。对于环保所带来的效益,采用清洁能源替代所减少的处理污染物的成本来表示,环境效益函数的数学表达如式(7)所示。
式中:Ei,t,CO2、Ei,t,NOx、Ei,t,SO2分别为项目i在第t年由于清洁能源替代所减少的CO2、NOX、SO2排放量;PCO2、PNOX、PSO2分别为单位CO2、NOX、SO2的处理成本。
2.1.4 安全效益函数
容载比是考核电网投资项目是否能够安全可靠运行的重要指标,其反映了变电设备容量与最大负荷的关系,过高或过低的容载比均会导致投资的经济性变差。安全效益函数用Bsec(ηi)来表示,如式(8)所示。
式中:θ和γ分别为容载比上、下限;α为电网剩余容量的影响系数;β为电网不足容量的影响系数;L为整个电网系统主线平均负荷。
2.1.5 投资能力惩罚函数
由于电网企业在投资中所投入的金额不能超过自身投资能力,因此设置投资能力惩罚函数。当对电网项目的投资总额超过其自身的投资能力时,再大的综合效益也将失去意义,且惩罚函数的结果会变成一个非常大的数值,最终的目标函数值会快速减少,该投资组合将被淘汰。投资能力惩罚函数如式(9)所示。
式中:Bi为第i个项目的投资额;B为电网企业的投资能力。当投资额未超出投资能力时,惩罚函数无效;当投资额超过投资能力时,巨大的惩罚函数值将导致电网公司无法进行投资。
2.2 约束条件
对于电网项目投资决策的研究,通常涉及多方面的约束,其中,投资能力约束、负荷需求约束、电网资源约束及投资项目约束是考虑的重点,以下对各约束条件进行逐一分析。
1)投资能力约束
根据电网项目投资的实际情况,对各项目的总投资额须小于电网公司现有的投资能力,其约束如式(10)所示。
2)负荷需求约束
对各项目的投资还应保证在一定的规划期内某地区电网的新增容量满足负荷需求,其约束如式(11)所示。在投资前,通常需要调研当地的具体情况,根据实际的负荷需求情况来对项目进行投资。
式中:D为当地的负荷需求。
3)电网资源约束
电网项目投资过程中,也需要考虑人力资源、物力资源及财力资源的限制,为此,设计电网资源约束条件如下:
式中:si,t为项目i第t年对该资源的需求量;st为第t年可供给资源的最大量。
4)投资项目约束
电网不同项目之间的关系纷繁复杂,包含独立关系、互斥关系和从属关系等。由于不同关系之间的约束条件无法同时考虑,此处将项目独立作为基准情形进行研究。项目独立约束是指是否投资某个项目而不对投资另一个项目产生影响。当电网共有n个项目时,项目独立约束情况的表达式如下:
3 求解算法
3.1 经典和声搜索算法
电网投资组合问题具有非线性、多维度且涉及电力系统中不同要素等特点。混合整数规划法和动态规划法等算法对解决带有上述特点的电网投资组合问题的适用性较差且计算速度偏慢。这使得上述优化算法无法高效地对本模型进行求解。
近年来,为解决多目标、非线性优化等有关问题,学者们已提出并丰富了多种不同的优化算法。和声搜索算法是一种新颖的智能优化算法[21],它是受音乐家创作时不断调整各乐器音调最终汇成完美和声的过程所启发而产生的智能优化算法[22-23]。和声搜索算法对于带有非线性、多维度特点的电网投资组合优化问题,通过反复调整记忆库中的解变量,使函数值随着迭代次数的增加而不断收敛,从而来完成优化,因其计算逻辑简单,在求解组合优化问题时易跳出局部最优解,在解决电网投资组合优化问题方面颇具优势。经典和声算法的具体步骤如下。
1)定义问题和参数值
首先,假设最小化问题如式(14)所示:
式中:f(X)为目标函数;X为由决策变量xl组成的解向量,即和声向量;[xl,L,xl,U]为决策变量xl的可行解取值范围,xl,L表示取值范围下界,xl,U表示取值范围上界;m为决策变量总数。
其次,确定参数值。确定和声库大小NHMS,即种群规模;和声采纳率RHMCR,即从现有和声库LHM中取出一个和声的概率;和声微调率RPAR,即通过微调的方式取出和声的概率;和声微调带宽WBW,即进行微调的幅值;最大创作次数,即最大迭代次数Tmax。
2)初始化和声库
初始化和声库LHM。从X的解空间里随机生成数量为NHMS的和声向量X1,X2,…,XNHMS,并放入和声库LHM中,记录相应的f(X),和声库的形式为:
式中:xf,g为第g个解向量的第f个分量。
3)创作新和声
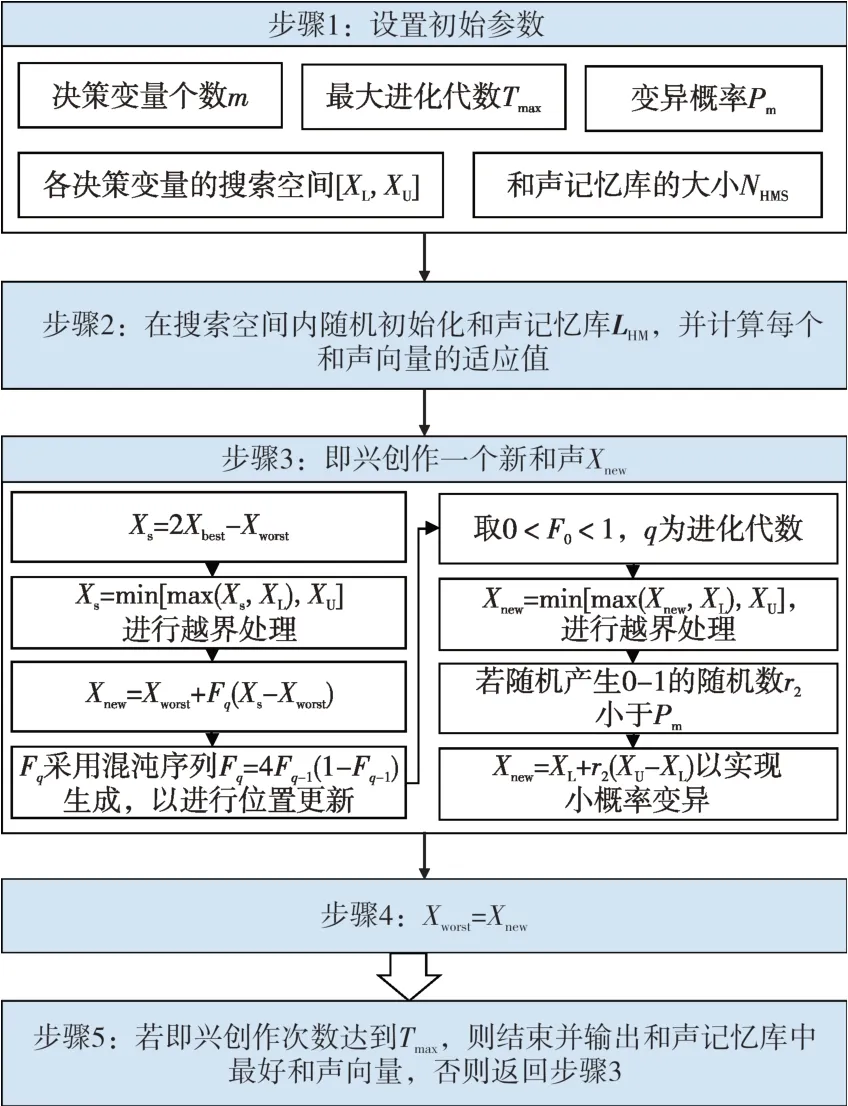
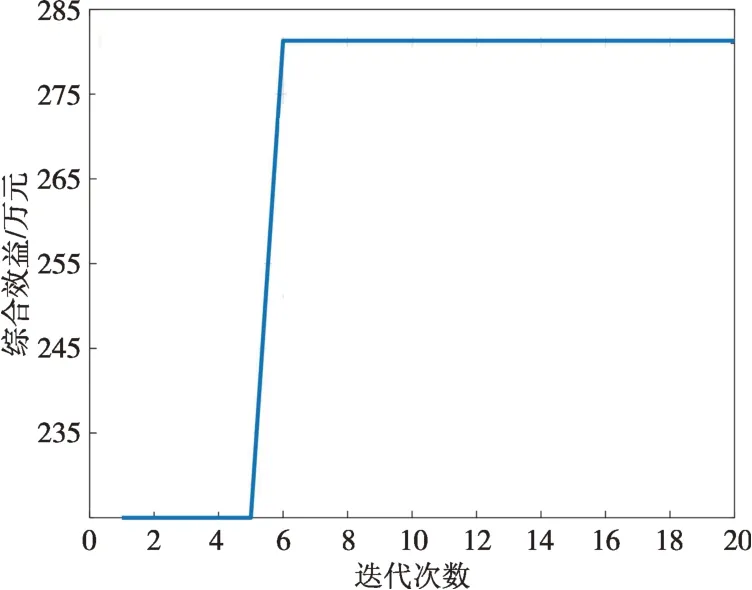
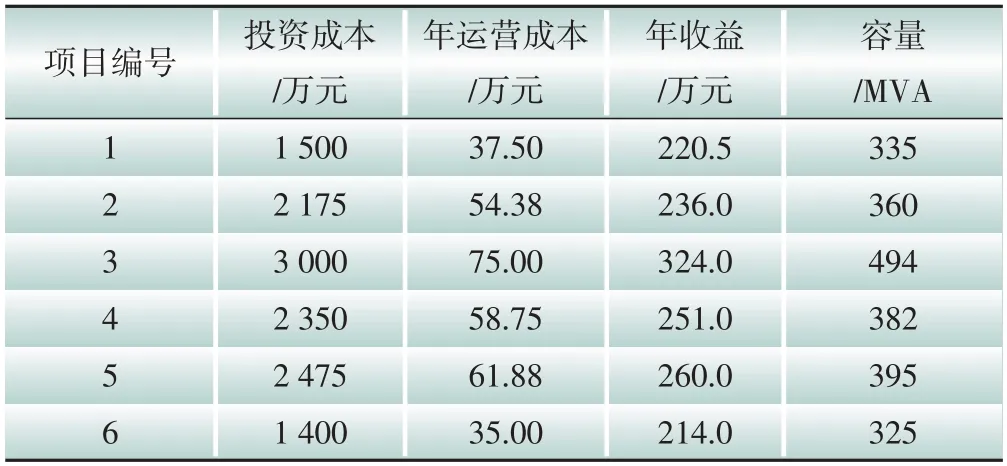
在区间[0,1]内产生一个随机数r1,与RHMCR比较,若r1 另外,若和声变量从和声库中取得,则需要对其进行微调,再次在区间[0,1]内产生一个随机数r2,若r2 4)更新和声库 对xl,new进行评价,若xl,new优于LHM中最差的目标函数值,则用xl,new取代最差的和声;否则,不做修改。 5)检查算法是否终止 若迭代次数达到最大创作次数则终止算法,否则重复步骤3)和步骤4)。 为克服算法存在的停滞现象,利用位置更新和小概率变异的方法取代传统和声搜索算法的音调微调操作,形成全局和声搜索算法。为更好地理解改进算法,3.1节已对经典的和声搜索算法步骤进行了详细阐述,对于改进的算法,重点阐述其与经典算法的区别及其优势。改进算法的详细步骤如图2所示[24-26]。其中,Xbest和Xworst分别为和声记忆库中最好和声与最差和声。 图2 全局和声搜索算法流程Fig.2 Flow chart of global harmony search algorithm 图3 全局和声搜索算法综合效益寻优结果Fig.3 Optimization results for the comprehensive benefits of global harmony search algorithm 全局和声搜索算法与传统算法的区别在于:首先,全局和声搜索算法不考虑参数RHMCR、RPAR、WBW,且增添了变异概率Pm;其次,种群更新方式不同,经典算法采用精英更新策略,即只有新的和声优于最差和声时才进行更新,而在全局和声搜索算法中,均须用新和声来替换最差和声。因此,全局和声搜索算法在整个计算周期内具有一定优势。在计算初期,种群较为分散,有利于算法进行全局搜索;在计算后期,各种群向最优解靠拢,有利于算法进行局部搜索。 算例拟对6 个备选的电网项目进行投资组合,拟定投资规划期为12年,期望投资回报率为7%,企业对该6 个电网项目的投资额总计10 000 万元。6个待选项目的投资成本、运营成本、收益及容量情况如表1所示。应用上文所提出的和声搜索算法,在MATLAB R2018a 平台中进行求解计算。待选项目参数及取值见表2。 表1 待选项目基本信息Table 1 Basic information of candidate items 表2 待选项目参数及取值Table 2 Parameters and values of candidate items 首先,采用Shapley值法确定不同效益函数在总目标函数中所占比重。效益函数集合为I={1,2,3,4},其中1代表经济效益函数,2代表社会效益函数,3 代表环保效益函数,4 代表安全效益函数。由于各子集对应的数值较大,为方便计算,进行归一化处理,集合I所有子集与对应的数值见表3。 表3 效益函数构成的子集及数值Table 3 Subsets and values of the benefit function 基于Shapley值的分摊方法,根据式(1)、式(2)和表3,计算得到Shapley值分别为0.007 5、0.057 5、0.030 8、0.154 2。进一步根据式(3)计算出不同效益函数的权重系数,ω1为0.32,ω2为0.26,ω3为0.29,ω4为0.13,从而获得最终的目标函数,并考虑当项目均各自独立时,构建投资组合决策模型。应用和声搜索算法对上述问题进行计算并获得结果,此处对算法进行参数设置:最大迭代次数Tmax=20,和声库大小NHMS=20,变异概率Pm=0.05。 进一步,为验证全局和声搜索算法的优越性,将粒子群算法、经典和声搜索算法作为对比方法。由于迭代次数会影响寻优效果,为了更好地进行对比,此处将最大迭代次数设为100。3 种算法的迭代过程如图4所示。 图4 3种算法迭代过程Fig.4 The iterative processes of three algorithms 由图4可知,全局和声搜索算法的收敛速度最快,优于经典和声搜索算法和粒子群算法,能够有效提升计算效率。 为验证获取不同效益函数在总目标函数中所占比重的意义,将通过差异化权重与等权重方式构建目标函数的结果进行对比。此处令和声搜索算法的参数不变,将不同效益函数的权重系数均取0.25,对模型进行再次求解。总目标函数值及各效益函数值的对比如表4所示。 表4 不同目标函数构建方法求解结果对比Table 4 Comparison of solution results obtained through different objective function construction methods万元 由表4可知,通过等权重目标函数方式求解得到的总目标函数值比差异化目标函数方式得到的总目标函数值低了37.05万元。这说明在各效益函数等权重的情况下,获取的总体效益值偏小,且各效益函数值呈现相等的情况,并未体现出效益指标之间的区别,在实际生产生活当中出现该情况的概率较低,为企业提供决策支撑的价值不大。而Shapley值法构建差异化权重目标函数的求解结果既能够获取优良的综合效益值,又能呈现各效益指标的特点,体现出效益分摊的合理性。同时,权重分配结果也能够反映出项目投资效益的侧重点和目前企业的投资倾向。根据计算结果,项目投资效益侧重在经济性与环保性方面,而安全效益与社会效益有待进一步加强。这为企业在未来权衡多维度效益的投资并调整投资策略提供了有力的决策支持。 综上所述,本文所建模型以综合效益最优为目标,统筹考虑投资需求、投资能力,进行电网项目投资组合优化,并运用和声搜索算法求解。最终得到优化结果为[1,1,0,1,1,1],其中1 表示项目入选,0表示项目落选。结果显示共有5个项目入选,由图3可知,综合效益值为281.53万元。 考虑到电网投资中所涉及的项目投资组合情况,在进行投资决策时须综合考虑相关约束条件及目标要求,既要满足投资需求,又要在投资能力允许的范围内安排各项目投资,最终实现综合效益的最优化。本文基于Shapley值法分摊各效益函数贡献度,进一步完善总目标函数的构建,并将全局和声搜索算法应用于电网投资组合问题求解当中,根据实例计算结果,得到以下结论: 1)将Shapley值法应用到效益函数的构建当中,能够使不同效益函数的贡献度得到有效分配,从而使目标函数的形成更贴合实际。同时,计算结果可为企业未来调整投资策略提供支撑。 2)根据全局和声搜索算法的计算结果,在权衡经济性、安全性、环保性及社会性的基础上,选择项目1—6 进行组合,能够获得最大的综合效益且该算法的运算效果更具优越性。 3)在进行决策时,以效益为核心,有益于统筹投资能力及效益水平。以投资能力为基础,合理确定电网投资规模,可确保合理的投资回报。 本文关于电网项目的投资决策主要计及电网投资的整体效益,从经济性、安全性、环保性及社会性的维度展开分析,提升了公司投资管控能力,有效支撑电网企业经营决策,实现电网企业可持续发展。为紧跟实际项目需求,不断提高投资精细化水平,未来研究的重点可延展到对电网投资进行归类,例如基础业务、智能业务、输变电业务等,并根据不同类型业务提出针对性、精细化的投资策略。3.2 全局和声搜索算法
4 算例分析
4.1 数据及参数设置
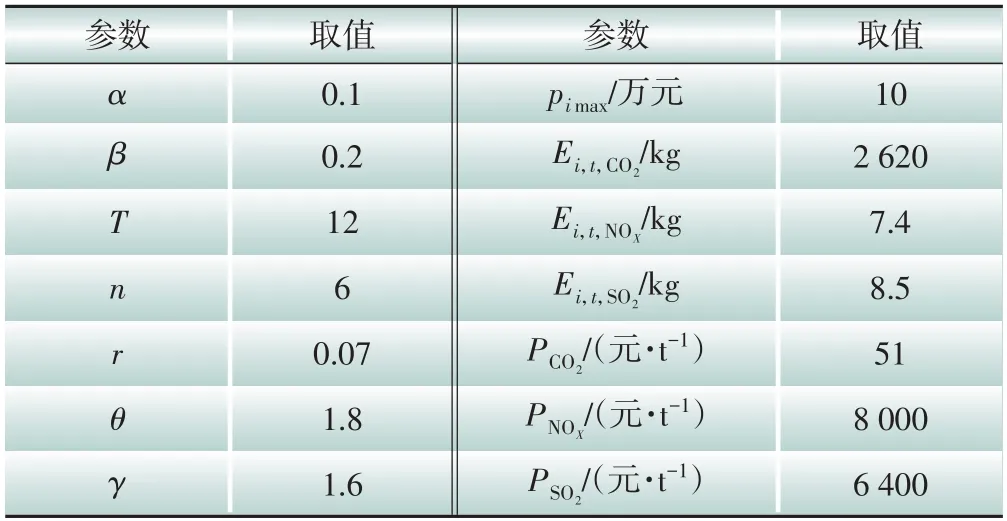
4.2 项目投资组合策略
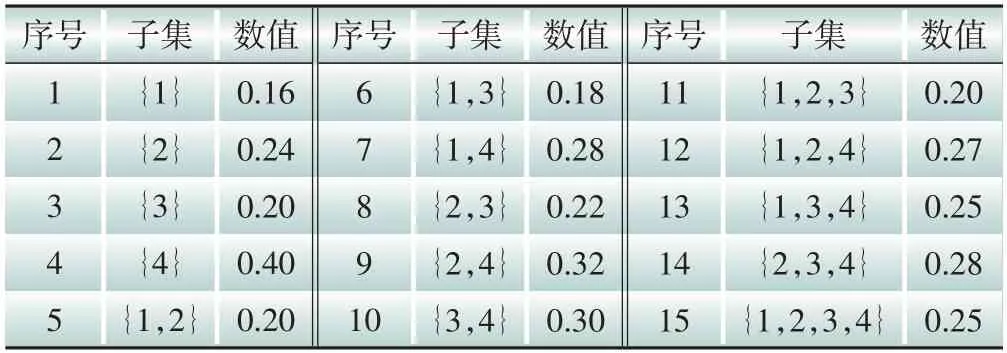


5 结论

