环境复杂度量化评价下的车位选择方法

陈泽辉, 彭育辉, 黄炜, 姚宇捷, 吴庆, 何维堃

(福州大学机械工程及自动化学院, 福建 福州 350108)

0 引言

目前全场景自动泊车难以实现, 自动泊车系统不同场景下泊车成功率差异较大[1], 车位选择对提升泊车成功率有较大意义. 已有关于车位选择方法的研究, 一类从选择主体出发, 研究主体特征与泊位特征的联系. 梁伟等[2]、Chaniotakis等[3]通过多项Logit模型建立个体特征至泊位特征的映射关系. 此类方法需要较大样本量来确保模型准确性, 且评价依赖于主体各项信息. 另一类方法则通过分析泊位客观属性对泊位评价后建立排序选择模型, 综合评价模型的建立包含指标选取、权重分配、量化评价3个步骤. 季彦婕等[4]利用熵权法与灰色关联度分析对可选车位排序,建立停车场泊位选择模型. Ding等[5]以层析分析法求解主观权重, 以数据差异化最大为目标, 建立拉格朗日函数来求解客观权重, 通过优劣解距离法完成综合评价, 建立私人共享车位选择模型. 此类方法由于应用客观赋权法(如熵权法等), 需要首先获得所有可选车位信息, 在计算单个车位指标权重时存在局限性. 上述研究存在以下两点问题: 1) 大多集中于结构化的停车场场景或特定场景下的车位选择, 指标选取依赖于该场景下的车位选择取向, 场景泛用性不强; 2) 方法应用时依赖全局场景信息, 无法对单个样本进行评价.

目前对于车位环境复杂度的评价研究主要集中在自动泊车系统的测试研究中. 无人系统自主等级评价体系框架[6]是根据已完成任务复杂度、环境复杂度和人工干预程度3个方面来量化评价无人系统的自主化级别的, 已被应用于自动泊车系统测试[7]. 通过提取真实数据、模拟数据和经验数据来获得自动泊车测试场景要素, 组合不同类型的环境要素以控制测试场景环境复杂度[8-9]. 上述研究往往通过模糊化的语句对环境复杂度进行分级, 通过人为设计与先验知识获得环境复杂度评级, 并无具体的量化评价方法, 无法应用于自动泊车系统车位选择.

为扩大车位选择方法场景泛用性, 本研究建立基于环境复杂度量化评价的车位选择方法. 在评价指标选取方面, 以现有研究涉及的车位环境因素为依据, 选取车位环境复杂度评价指标; 在权重计算方面, 提出层次分析法与局部有限信息结合的主客观赋权法以适应单个样本评价; 利用指标评价分级无明确界限且面向单个车位评价的特点, 应用模糊综合评价法在所求主因素突出权重基础上实现车位环境复杂度的量化, 为车位的选择提供决策依据.

1 车位环境复杂度评价指标与量化方法

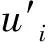
1.1 车位类型

车位类型(u1)包括垂直(V)、平行(P)和斜向(O)车位. 与Ding等[5]所提出的不同类型车位难度划分不同, 在自动泊车路径规划中, 平行泊车路径往往由多段曲线构成, 需要考虑更多约束, 相对于其他两种泊车形式而言难度较大, 而斜向车位由于角度不确定性, 形式较多, 故斜向车位路径规划难度大于垂直车位. 在车位识别方面, 斜向车位的识别率低于垂直车位和平行车位[10]. 故在泊车规划难度方面, 平行车位>斜向车位>垂直车位; 在车位识别难度方面, 斜向车位>平行车位=垂直车位. 考虑到斜向车位识别率仅略低于其余两种, 建立判断矩阵为

(1)

为扩大赋值区分度, 不对所求特征向量做归一化处理, 求解后将{平行泊车位, 斜向泊车位, 垂直泊车位}按相对难度表示为{0.846 8, 0.466 0, 0.256 5}.

1.2 车位线属性

车位线能够明确泊车位置, 使目标车位便于自动泊车系统识别和规划路径. 此外, 车位线还能够规范两侧停泊车辆位姿, 避免目标车位过于狭窄. 同等情况下, 应尽量选择具有车位线的车位. 与车位类型指标相同, 可将车位线属性(u2)的3种情况{无车位线, 车位线模糊, 有车位线}表示为{0.846 8, 0.466 0, 0.256 5}.

1.3 车位两侧占用情况

目标车位两侧的占用情况(u3)会影响泊车规划的避障约束富裕程度. 在通常情况下, 目标车位周围空间越大, 就越容易完成最终的泊车入库. 根据各情况相对难度, 建立判断矩阵为

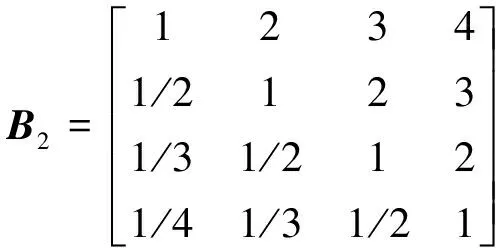
(2)

依照相对难度将{两侧皆占用, 单侧占用且另一侧有障碍物遮挡, 仅单侧占用, 两侧无占用}表示为{0.813 5, 0.482 6, 0.278 7, 0.166 1}.

1.4 车位边界曲率

定义泊车位所在道路向路内方向弯曲时车位边界曲率(u4)为正. 当车位边界道路具有正曲率时, 如图1(a)所示, 库内空间可能会被两侧车辆侵占, 造成车位狭窄; 反之, 道路向路外弯曲时, 如图1(b)所示, 泊车空间将有较大富余, 泊车难度降低.

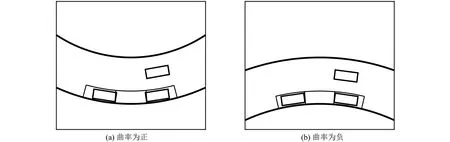
图1 车位边界曲率示意Fig.1 Boundary curvature of parking space

我国道路设计最小半径极限值为20 m[11], 则道路曲率取值范围[κmin,κmax]为[-1/20, 1/20],u4的规范化方法为

(3)

1.5 泊车通道宽度

充裕的泊车通道宽度(u5)能够降低待泊车辆一次入库的难度. 由于该指标数据范围较大, 且数值较小时难度变化更大, 更具区分意义, 因此采用指数函数将该数据映射至[0, 1]区间. 即

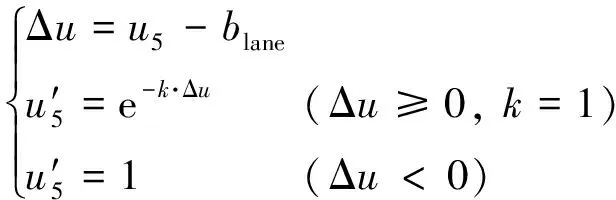
(4)

式中:blane为各类型车位所需最小泊车通道宽度[12];k为缩放系数, 由数据取值范围决定.

1.6 车位尺寸

车位尺寸(u6)直接影响停车难度, 是车位环境复杂度量化研究中必须考虑的关键因素, 车位尺寸指标量化时主要考虑其在平行于道路方向上的车位入口尺寸.对于平行车位, 如图2所示, 将车辆简化为矩形, 其各顶点分别为A、B、C、D, 车辆行驶轨迹圆心为O, 最小车位尺寸(SP)应满足

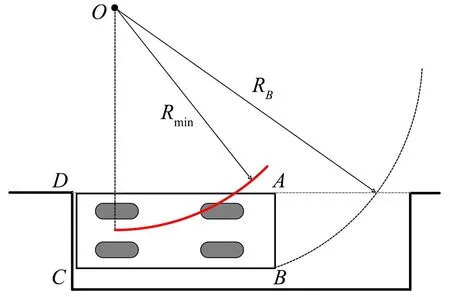
图2 平行泊车最小车位尺寸Fig.2 Minimum parking size for parallel parking

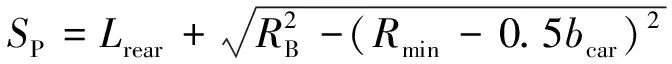
(5)

式中:Lrear为车辆后悬长度;RB为车辆顶点B运动半径;Rmin为车辆后轴中心最小转弯半径;bcar为车辆宽度.

对于垂直泊车与斜向泊车, 由于泊车路径后段为直线, 不考虑泊车通道宽度的情况下车辆能够在库外完成姿态调整, 故最小车位尺寸满足停车开门即可. 垂直泊车与斜向泊车所需最小车位尺寸分别记为SV与SO, 其计算公式分别为

SV=bcar+2(δhuman+δdoor)

(6)

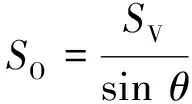
(7)

式中:δhuman为人体平均胸厚, 取0.20 m[13];δdoor为车门厚度, 取0.15 m[14];θ为车位与道路所成夹角.

车位尺寸指标规范化方法为

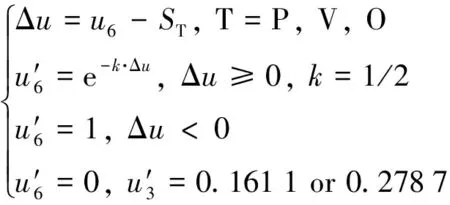
(8)

式中:ST为各类型车位最小尺寸; T为车位类型.

1.7 车位障碍物情况

目标车位周围存在障碍物, 会有一定概率遮挡车位, 使车位难以被自动泊车系统识别. 同时, 障碍物的存在对泊车路径求解也会造成一定的压力. 在泊车过程中, 理想情况下车身往往需要经过车位入口中点, 如图3中的M点. 因此利用障碍物中心至该点的欧氏距离来衡量障碍物对泊车难度的影响. 同时, 为简化计算, 将障碍物表示为以障碍物几何中心(图3中的O点)为圆心, 几何中心至障碍物轮廓最大距离为半径(Robs)的圆. 当车位四周存在多个障碍物时, 取距离M点最近的障碍物计算. 障碍物指标(u7)的规范化方法为

(9)

图3 车位障碍物情况Fig.3 Obstruction near parking space

2 基于主因素突出综合权重的模糊综合评价

在车位复杂度评价指标体系中, 泊车通道宽度、车位尺寸[2]、车位障碍物情况对评价结果起到决定性作用, 因此将评价指标分为一般指标与决定性指标, 如图4所示. 在层次分析法基础上引入决定性指标规范化后的平方和归一化数值来克服其主观性, 确定综合权重.

图4 车位环境复杂度评价指标体系划分Fig.4 Classification of environment complexity evaluation index system

2.1 指标初级权重确定

层次分析法通过因素间两两比较的形式来获取各指标间的相对重要程度, 并以此确定权重. 决定性指标集合(Ukey)与余下指标共同构成指标集合(Ugeneral), 参与层次分析法求解, 经过一致性检验后得到初级权重向量(W′), 即

Ugeneral={u1,u2,u3,u4,Ukey},Ukey={u5,u6,u7}

(10)

W′=(w1,w2,w3,w4,wkey)

(11)

式中:wkey表示Ukey所对应的权重.

2.2 指标综合权重确定

设ux, y表示第x个车位的第y个指标的规范化取值, 则第x个车位的各决定性指标权重为

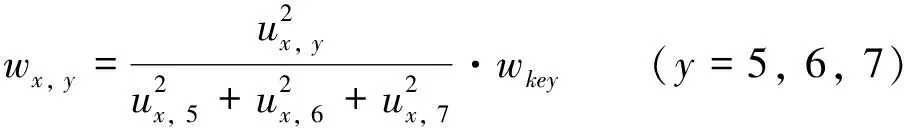
(12)

由此得到第x个车位的主因素突出型综合权重向量为

Wx=(w1,w2,w3,w4,wx, 5,wx, 6,wx, 7)

2.3 模糊综合评价

在车位环境复杂度量化评价中, 各个指标评价结果等级之间没有明确的界线, 因此引入模糊理论, 利用隶属度函数来描述泊车指标. 本研究评价结果集合(F)包含4个等级, 即{不复杂F1, 稍复杂F2, 较复杂F3, 极复杂F4}. 隶属度函数采用半梯形与三角形结合的方式, 指标各等级划分准则见表1. 其中,fj表示各指标在各难度上的划分标度,j=1, 2, 3, 4. 表中泊车通道宽度难度划分参考文献[12]和[15]; 车位尺寸难度划分参考文献[16]; 其余指标难度划分由专家直接指定.

表1 指标评价等级划分准则

3 仿真测试

基于Matlab模拟一组停车位. 其中将车位a～c设计为难度递增, 验证评价方法是否能正确反映车位环境复杂度; 车位d和e为对照车位, 将不同赋权方法与模糊综合评价法组合来进行评价, 验证评价方法是否能在决定性指标趋近临界值时赋予其较大权重, 以提升评价结果的准确性. 以目标车位近道路外侧边界中点为原点建立车位模型, 车位线尺寸参考文献[16], 设置为6.0 m×2.5 m, 各车位可视化后的结果如图5所示.

图5 可视化泊车环境模拟场景Fig.5 Visual simulation conditions of parking

为验证实验所设车位复杂度, 利用自动驾驶强化学习环境库highway-env搭建车位a～e, 并利用TD3和HER算法的组合对各车位训练2×105步, 得到泊车成功率变化, 如图6所示. 由图6可知, 车位a～e的复杂度依次递增.

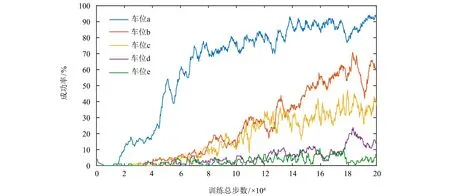
图6 训练成功率Fig.6 Success rate in learning

3.1 权重计算

构建判断矩阵(B), 即

(14)

求解该矩阵的最大特征值(λmax)所对应特征向量(T), 归一化后所得指标的初级权重矩阵为

W′=(0.062 7, 0.121 9, 0.200 3, 0.062 7, 0.552 4)

(15)

决定性指标整体占有较大权重.

为避免判断矩阵前后矛盾, 经一致性检验后, 利用式(12)求解各车位的各决定性指标权重, 对复杂决定性指标突出赋权, 结合初级权重得到主因素突出型综合权重矩阵(W), 最终权重结果如表2所示.

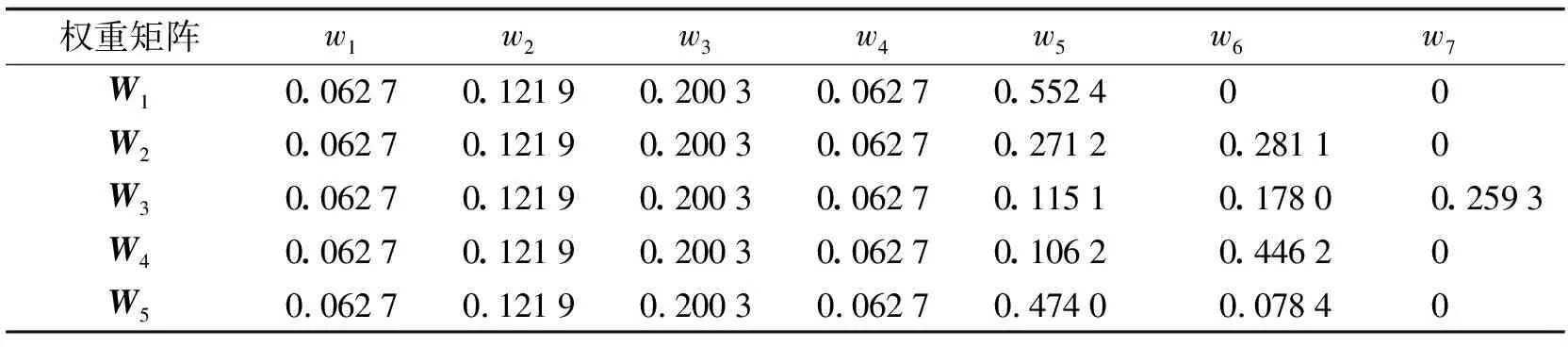
表2 综合权重计算结果

3.2 评价结果分析

通过隶属度函数将指标规范化数据映射至评语集合(F), 得到各样本模糊评判矩阵(Eh).结合各车位主因素突出型权重矩阵(Wh)求得最终评价结果矩阵(Qh),h为评价样本序号. 上述过程可表示为

Qh=Wh·Eh(h=1, 2, 3, 4, 5)

(16)

(17)

根据最大隶属度原则确定各车位复杂度等级, 结果为车位a不复杂、车位b稍复杂、车位c较复杂、车位d极复杂、车位e极复杂. 评价结果可正确反映图6中的车位复杂度变化, 泊车时应选择复杂度最低的车位a, 当两车位评价结果相同时, 应选择该评价结果隶属度较低的车位.

以图6所示深度强化学习训练中代理达到成功率最大值表示自动泊车系统在该车位下实际泊车成功率, 可得车位a～e泊车成功率分别为94%、71%、47%、24%、11%, 依照本方法选择车位a, 相较于余下车位在泊车成功率上均有较大提升, 能够有效提升自动泊车系统泊车成功率.

3.3 赋权方法分析

分别应用本研究方法、层次分析法、熵权法与层次分析法-熵权法4种赋权方法计算对照样本车位d与e的各项指标权重, 其中熵权法的主要思想是通过样本指标中数据的混乱程度来确定权重系数[16], 目的在于扩大最终评价结果的区分度. 权重计算结果如图7所示, 基于以上权重得到评价结果如图8所示. 仅有本研究方法做出正确的评价, 两车位结果均为“极复杂”. 其余方法由于临界决定性指标权重分配不足且“不复杂”成分过高, 会低估对照车位的环境复杂度.

图7 不同方法求得的车位权重Fig.7 Weights of parking space solved by different methods

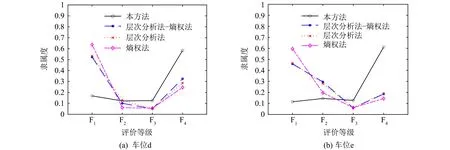
图8 不同权重下得到的车位评价结果Fig.8 Evaluation results of parking space solved by different weights

层次分析法单纯从先验知识出发, 能在一定程度上使得权重分配更为合理, 但由于不考虑数据的变化, 该方法灵活性较差. 熵权法借助信息熵描述指标数据差异化程度, 旨在扩大最终评价结果区分度, 但样本之间相互影响程度较大, 计算结果不够稳定. 层次分析法-熵权法是二者所求权重的简单线性叠加, 中和二者的优点与缺点. 本研究所提方法对变化不大的指标采用层次分析法求解权重, 再根据各决定性指标复杂程度突出赋权, 提升评价方法的合理性与灵活性.

此外, 在实际应用时对算法实时性应有较高要求, 即需要评价各个赋权算法时间复杂度与空间复杂度, 通常采用O(n)表示, 反映两种复杂度随规模n的变化趋势.对于时间复杂度, 层次分析法可以在实际运行之前完成运算, 此处仅讨论在实际运行时需要的运算量.本研究中指标数为7, 熵权法需要计算概率矩阵、信息熵与各指标权重, 时间复杂度为O(7n+7n+n).本研究所提方法仅需求解3个决定性指标权重, 时间复杂度为O(3n).当n→∞时两种方法时间复杂度均为O(n), 但实际应用时样本规模一般不大, 系数不可忽略, 因此实际运行中各算法在时间复杂度上的排序为层次分析法<本研究方法<熵权法=层次分析法-熵权法.

对于空间复杂度, 层次分析法可以离线完成计算, 所需空间不会因规模增大而增大, 空间复杂度为O(1).本研究算法由于对车位逐个评价, 储存空间可以重复利用, 空间复杂度同样为O(1).熵权法每新增1个样本都需要额外新增储存空间, 且所需空间均随规模增大而线性变化, 空间复杂度为O(n).同理, 层次分析法-熵权法空间复杂度也为O(n).综上, 各算法在空间复杂度上的排序为层次分析法=本研究方法<熵权法=层次分析法-熵权法.

4 结语

研究在层次分析法基础上引入决定性指标规范化后的平方和归一化值来求解主因素突出型权重, 结合权重系数提出一种基于模糊理论的车位环境复杂度量化评价方法. 通过对比分析可知, 本研究所提评价方法相较于现有车位评价方法, 在面向单个样本时所得评价结果更具合理性, 同时具有较低的时间与空间复杂度, 对于自动泊车系统的泊车成功率有较大提升.

未来应进一步完善车位环境复杂度评价指标体系. ① 影响车位环境复杂度的因素众多, 应进一步补充评价指标体系, 如可能影响自动泊车感知系统的光照、天气等因素; ② 对所提指标进行关联性分析, 进一步提炼评价指标体系, 减少车位环境复杂度重复计算; ③ 障碍物指标中应进一步将动态障碍物纳入考虑范畴.