基于随机游走麻雀搜索算法的多特征结构尺寸熔融沉积成型工艺参数优化

郭润兰, 薛 凯, 邓文强, 范雅琼, 王虎林

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

由于对低成本原型和小批量耐用塑料成品的需求增加,所以熔融沉积成型(fused deposition modeling, FDM)工艺成为最具吸引力的数字制造工艺之一.因工艺参数会影响样件的尺寸精度[1-2],故参照常规经验对不同的结构设置常见典型特征结构,得出普适性的参数组合,从而提高打印精度.为优化FDM工艺参数,提高样件的尺寸精度,国内外学者进行了大量的研究和尝试.Padhi等[3]以田口法[4]研究了不同工艺参数对样件尺寸精度的影响,将模糊理论与田口法结合获得了最优的工艺参数. 韩善灵等[5]通过建立等体积率公式,最终在保证竖直方向精度的前提下,获得了最优的水平方向精度.陈松茂等[6]通过对3种不同尺寸规格的样件进行FDM实验,研究了不同尺寸规格和精度指标对优化结果的影响,获得了不同样件规格的最优工艺参数.朱晨颖等[7]利用MATLAB分析了3个参数对制件表面质量的影响机理,确定了较优的参数方案.陆星宇等[8]基于熵权TOPSIS模型对实验结果进行探究,得出了最优工艺参数组合方案.冯建军等[9]根据多元回归分析建立了单目标参数最优方案预测的数学模型,为选取最优方案提供了极大帮助.Zhang等[10]以挤压速度、填充速度、线宽补偿和分层厚度为实验变量,以样件的长、宽尺寸精度为优化对象,采用稳健设计和多指标模糊综合评价方法获得了最优工艺参数.Fountas等[11]以沉积角度、分层厚度和填充率为实验变量,以样件的长、宽、高尺寸精度和成型时间为优化对象,采用田口法、病毒遗传算法、极差和方差分析法获得了最优的工艺参数组合.刘健等[12]在正交试验的基础上,利用综合平衡法处理最优工艺参数组合.Sajan等[13]通过考虑6个参数对制件几何精度的影响,得到了各参数对表面光洁度和几何精度的影响因子.Mahmood等[14]分析了相同尺寸时样件不同特征结构的绝对误差,确定了各特征结构尺寸与建模尺寸之间的变化关系,并在此基础上确定了最优的工艺参数组合.

以上研究多以样件的长、宽、高尺寸为研究对象,较少考虑多特征结构尺寸对分析结果的影响,或考虑的特征结构尺寸比较单一.此外,在数据处理方法上依靠人工计算结果,对结果的全局性、可能存在的最优解未考虑.同时,部分搜索算法寻优速度慢,容易陷入局部最优解并导致优化结果不理想.

鉴于此,本文以分层厚度、喷头温度、打印速度和填充率为实验变量,以样件不同特征结构尺寸的相对误差为优化对象,通过正交试验设计获取实验数据,并采用田口法和灰色关联法[15]对实验数据进行处理,利用随机游走的麻雀搜索算法获得最优的工艺参数组合,从而提高样件打印的整体尺寸精度.

1 随机游走的麻雀搜索算法

麻雀搜索算法(sparrow search algorithm,SSA)[16]是新颖的群智能优化算法.该算法受到麻雀觅食和反捕食活动的启发,把麻雀分成了发现者和加入者.发现者负责为整个种群搜索到具有丰富食物的区域;加入者总是能搜索到提供最好食物的发现者,然后在发现者周围觅食或者与其一起觅食.由n只麻雀组成的种群可表示为

(1)

式中:d为待优化问题变量的维数;n为麻雀的数量.

那么,所有麻雀的适应度值可表示为

(2)

式中:f为适应度值.

在搜索过程中,具有较高适应度值的发现者会优先获得食物.同时,因为发现者要为整个种群寻找食物,并且提供觅食方向,所以发现者的觅食搜索范围更大.在每次迭代的过程中,发现者的位置更新为

(3)

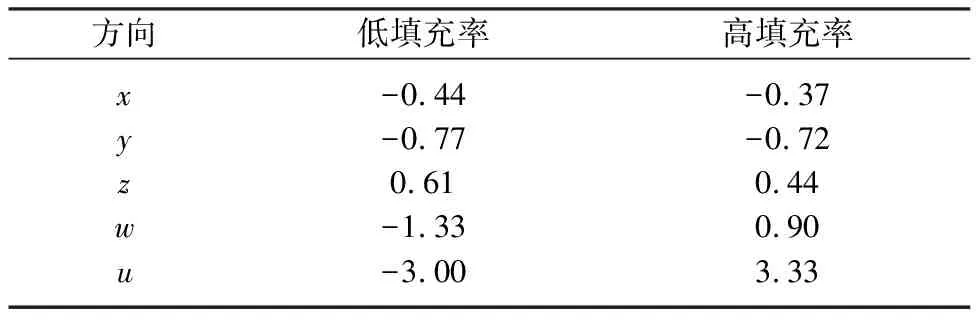
式中:t为当前迭代次数;itermax为常数,表示最大迭代次数;Xij表示第i个麻雀在第j维中的位置信息;α∈(0,1]为随机数;R2∈[0,1]和ST∈[0.5,1]分别为预警值和安全值;Q为服从正态分布的随机数;L为1×d的矩阵,其中每个元素全部为1.当R2

在觅食过程中,一些加入者一旦察觉到发现者找到了更好的食物,会立即离开飞过去争夺食物.如果战胜了发现者,马上可以获得该发现者的食物.否则,它们只能继续处在底端的觅食位置,或者飞往其他地方觅食.

加入者的位置更新为

(4)

式中:XP为目前发现者所占据的最优位置;Xworst为当前全局最差的位置;A为1×d的矩阵,其中每个元素随机赋值为1或-1,并且A+=AT(AAT)-1.当i>n/2时,表明适应度值较低的第i个加入者没有获得食物,处于十分饥饿的状态,此时需要飞往其他地方觅食,以获得更多的能量.

在实验中,设定意识到危险的麻雀占总数量的20%,这些麻雀的初始位置是在种群中随机产生的,表达式为

(5)

式中:Xbest为当前全局最优位置,表示此时这只麻雀所处位置是种群中最好也是最安全的;β为步长控制参数,是服从均值为0、方差为1正态分布的随机数;K∈[-1,1]为随机数,表示麻雀移动的方向同时也控制步长;fi为当前麻雀个体的适应度值;fg和fw分别为当前全局最佳和最差的适应度值;ε为避免分母出现零而补充的常数.当fi>fg时,表示麻雀此时正处于种群的边缘,极其容易受到捕食者的攻击;当fi=fg时,表示处于种群中间的麻雀意识到了危险,需要靠近其他麻雀从而尽量减少被捕食的风险.

随机游走的过程可表示为

(6)

式中:X(t)为随机游走的步数集;cussum为计算累加和;t为随机游走的步数(本文取最大迭代次数);r(t)为随机函数,即

(7)

式中:rand为处于[0,1]的随机数.

由于可行范围存在边界,所以不能直接用式(1)更新麻雀的位置.为确保在可行域范围内随机游走,需要进行归一化处理,即

(8)

本文为了验证随机游走的麻雀搜索算法在打印参数优化过程的效果,以灰色关联度作为衡量优化效果的指标,在获得算法最优方案之后,对方案进行成型实验验证,并与常规方法所得样件进行对比,从而证明随机游走的麻雀搜索算法在熔融沉积成型参数优化中的可行性.

2 熔融沉积成型实验

本文选取分层厚度/mm、喷头温度/℃、打印速度/(mm·s-1)和填充率/%作为优化设计的实验变量.为保证优化结果的准确性,以长x、宽y、高z、圆外径w和孔内径u为特征,设计了包含多种特征结构尺寸的实验模型.设计尺寸分别为x=45 mm,y=25 mm,z=12 mm,w=20 mm,u=10 mm.样件模型如图1所示.

图1 FDM实验样件模型Fig.1 FDM experimental sample model

为探究各工艺参数对样件成型精度的影响,在参考范围内均匀取4个正交试验水平,结果如表1所列.根据表1设计了L16(44)正交试验,结果如表2所列.

表1 正交试验因素和水平

表2 正交试验表

在获得实验参数之后,按照实验序号依次进行成型实验得到样件,如图2所示.

图2 实验样件Fig.2 Experimental sample

对表2的16个成型方案分别进行成型实验.成型过程由极光尔沃A6型打印机完成,打印喷头的直径为0.4 mm,填充结构采用默认网格结构,热床温度保持一定,且在成型过程中打印舱门闭合.在成型实验完成后,测量样件各项特征结构的尺寸,并作为下一步分析的原始数据.为保证测量结果的准确性,所有样件均自然冷却24 h后再进行测量,测量工具为Mitutoyo 530-102(N15R)游标卡尺,测量时每项指标均在有效测量位置上测量3次.测量结果如表3所列.

表3 实验样件尺寸测量结果

样件各特征结构的尺寸大小不同,如果采用绝对误差作为评价指标,就会因尺寸大小的差异而造成尺寸误差的变化,进而难以准确地表述不同特征结构的尺寸误差.因此,本文以各结构尺寸的相对误差为评价指标,从而消除尺寸大小不同对分析结果的影响,提高优化结果的准确性.样件各特征结构的尺寸相对误差为

(9)

式中:λi为实际测量尺寸,i=1,2,3;λ为理论尺寸.

田口法属于高效、系统的实验方法,在保证实验设计科学性的前提下,可以大大提高实验效率.田口法将信噪比作为产品质量特性的评价标准,以此反映实验过程中衡量指标的波动情况.其中,静态信噪比可以分为望大特性信噪比、望小特性信噪比和望目特性信噪比.样件尺寸的相对误差属于越小越好的指标,即静态望小特性信噪比,计算方法为

(10)

式中:n=3;ei为尺寸误差百分比.

为提高数据处理的准确性,考虑数据波动对分析结果的影响,计算时将样件不同特征结构尺寸的3个相对误差代入式(10)进行计算.

根据式(10)对实验测量数据进行计算,得到16个FDM样件的各特征结构尺寸相对误差信噪比,如图3所示.

图3 相对误差信噪比Fig.3 Relative error SNR

为提高优化结果的准确性和优化效率,使用灰色关联法对数据进行处理.从已知数据矩阵中找出理想参考方案,对评价矩阵进行无量纲规范化处理;同时,依据权重系数计算评价矩阵获得各方案的关联度,得到各实验方案的灰色关联度,如表4所示.在灰色关联分析法中,灰色关联度是方案优劣的评价指标,灰色关联度越高表明该方案越接近理想方案.由表4可以看出,在实验方案中获得较高灰色关联度的水平差值很小,最高值为0.465 6.

表4 不同参数下灰色关联度

利用极差和方差分析法研究各工艺参数对样件综合尺寸的影响.根据极差值可以得出,分层厚度对灰色关联度的影响最大,填充率对其影响最小,结果如表5所列.同时,还可以得出各工艺参数对FDM样件综合尺寸相对误差信噪比的影响程度,即:分层厚度>喷头温度>打印速度>填充率.

表5 各因素水平灰色关联度的极差

根据实验结果可以看出:分层厚度、填充率与灰色关联度呈正相关,随着分层厚度和填充率逐渐增大,灰色关联度总体呈上升趋势,且分层厚度对灰色关联度的影响更大,相关系数更高;而喷头温度、打印速度与灰色关联度呈负相关,随着喷头温度和打印速度逐渐增大,灰色关联度总体呈下降趋势,二者对于灰色关联度的影响效果差别很小,但是在喷头温度高于215 ℃之后喷头温度与灰色关联度又呈正相关.通过深入分析可以发现:随着分层厚度和填充率逐渐增大,熔融聚乳酸(polylactic acid,PLA)材料的热胀冷缩效应降低,样件的变形量减小,工艺参数更加接近理想方案,因而灰色关联度上升;而喷头温度和打印速度增大之后,熔融PLA材料的流动性变大,进而引起样件变形量的增大,因而灰色关联度下降.综上所述,当分层厚度为0.3 mm,喷头温度为220 ℃,打印速度为20 mm/s,填充率为25%时,可得极差和方差分析法的最优方案,此时灰色关联度为0.484 4.

3 随机游走的麻雀搜索算法实验

在完成正交试验并取得多目标优化指标之后,在MATLAB平台拟合4个工艺参数与灰色关联度之间的函数.经过多次拟合,最终选定拟合效果最优的函数关系表达式为

(11)

式中:x1为分层厚度,mm;x2为喷头温度,℃;x3为打印速度,mm/s;x4为填充率,%.

构建随机游走的麻雀搜索算法模型,根据原始麻雀算法设置参数.将麻雀种群数量设为1 000,发现者比例设为0.8,意识到有危险的麻雀比例设为0.2,种群中预警值设为0.5,上、下边界根据正交试验参数分别设为lb={0.15,205,20,15}和ub={0.35,230,55,55},模型首次迭代次数设为100.随机游走的麻雀搜索算法结果迭代曲线如图4所示.由图4a可以看出,在迭代60次时出现最优解,但不能排除迭代次数较少的影响.为确保结果的可靠性,调整实验参数进行多次重复实验,分别得到图4b～d的曲线.可以看出:在迭代110次左右时,模型得到最优解0.591;同时,经过400次迭代与200次迭代的结果相同.此时可以确定,在麻雀种群数量设为1 000,发现者比例设为0.7,意识到有危险的麻雀比例设为0.2,种群中预警值设为0.6,上下边界分别设为lb={0.15,205,20,15}和ub={0.35,230,55,55},迭代次数设为110时,可得算法最优解.与原始麻雀搜索算法相比,随机游走的麻雀搜索算法收敛速度更快,寻优范围更大,并且在随机游走过程中更好地避免陷入局部最优,同时寻优结果更好.

图4 随机游走的麻雀搜索算法结果迭代曲线Fig.4 Iterative curve of the result of the sparrow search algorithm for random walk

随机游走的麻雀搜索算法结果如表6所示.可以看出,随机游走的麻雀搜索算法优化效果明显且结果稳定,在实验过程中适应度值多次稳定在0.56左右,最高值为0.591,相比极差和方差分析法适应度值最高提升了27%.在分层厚度0.35 mm、喷头温度225 ℃、打印速度20 mm/s和填充率17%的条件下进行成型实验,对适应度值为0.591的样件进行测量,并与极差和方差分析法所成型样件进行对比,发现实际精度提升了20%.

表6 随机游走的麻雀搜索算法结果

高填充率与低填充率结果对比如表7所列.可以看出,在适应度值差值较小时,分层厚度、喷头温度和打印速度变化范围很小,但是填充率变化很大,差值为27%～34%.在分层厚度为0.15～0.35 mm,喷头温度为205～230 ℃,打印速度为20～55 mm/s,填充率为15%～55%时,使用随机游走的麻雀搜索算法保留159组有效数据,对填充率出现两极的问题进行分析,发现在适应度值相差1%的条件下填充率在20%以下和40%以上的情况分别占了46%和54%.从低填充率和高填充率中分别随机选取适应度值相差小于1%的10组数据进行验证.

表7 高填充率与低填充率结果对比

按照多次测量取平均值的方法,在样件各尺寸方向上分别测量3次并取平均值.可以发现,在其他3个参数相近的情况下,高填充率成型样件相比低填充率成型样件在长、宽、高和外圆的尺寸误差绝对值更小,而在内圆的尺寸误差绝对值更大,如表7所列.主要原因是:在样件打印完成后的冷却过程中,熔融PLA材料会因温度下降而收缩,较低的填充率导致内部有更大的收缩空间,结果表现就是尺寸变化更大,精度较低;而较高填充率的样件拥有较小的内部空间,从而降低了可收缩范围,使其尺寸更加精确.在熔融沉积成型过程中,较高的填充率意味着较长的打印时间,但是在权衡时间与精度的关系中,仍然需要优先考虑分层厚度,其次考虑喷头温度、打印速度和填充率.不同填充率下实验样件如图5所示.

图5 实验样件Fig.5 Experimental sample

4 结论

为优化FDM工艺参数,提高样件的尺寸精度,本文考虑了多种典型结构尺寸对优化结果的影响;以FDM分层厚度、喷头温度、打印速度和填充率为实验变量,设计了4因素4水平的正交试验.利用田口法将样件各特征结构尺寸的相对误差转化为信噪比,通过灰色关联法将多个单目标优化问题转换为优化指标唯一的多目标优化问题,并对实验数据进行处理分析.通过随机游走的麻雀搜索算法获得了最优的工艺参数组合,并通过实验验证了优化结果的准确性.本文的主要结论如下:

1) 同组工艺参数对不同特征结构尺寸相对误差的影响不同,其中,内圆的尺寸相对误差最大,其次是高、外圆、长和宽的尺寸相对误差.由此说明,在进行FDM工艺参数优化的过程中,仅考虑样件长、宽、高尺寸精度对分析结果的影响难以获得较好的优化效果,有必要考虑尽可能多的典型特征结构尺寸对优化结果的影响.同时,实验结果验证了本文研究的必要性和可行性.

2) 通过随机游走的麻雀搜索算法所得最优结果可知,喷头直径为0.4 mm时,在分层厚度0.35 mm、喷头温度225 ℃、打印速度20 mm/s和填充率17%的情况下,成型样件精度误差达到最小值,与利用极差和方差分析法所得结果相比精度提高了27%.随机游走的麻雀搜索算法表现出更小的分辨率,能够在给定范围内得出更优的结果.

3) 寻优结果中,适应度值相同时,其他参数差异不大,填充率表现出两极化的问题,即在填充率为17%和44%时所得适应度值相同.经过成型实验对比发现,高填充率样件在各方向的精度均优于低填充率样件.主要原因可能是,熔融PLA材料在室温下收缩导致微小形变,在打印完成后温度降低,填充率高的样件收缩率较小,而填充率低的样件收缩率较大,导致精度较低.