D2D网络中基于多目标优化的计算卸载策略

陈 琦，李晶晶

（华南师范大学计算机学院，广东 广州 510620）

0 引言

随着移动通信技术的发展和智能终端的普及，用户对网络服务质量、请求时延等网络性能的要求越来越高。尽管移动设备的处理能力越来越强大，但依然无法在短时间内处理计算密集型或时延敏感型计算任务。为此，研究者们提出了移动边缘计算（Mobile Edge Computing）［1］，并应用在不同的场景中（如5G网络［2］、物联网［3］等）。作为移动边缘计算的关键技术之一，计算卸载［4］是指移动设备将部分或全部计算任务交给云计算［5］处理的技术，用于解决移动设备在资源存储、计算性能以及能效等方面存在不足的问题。

传统的移动边缘计算卸载通过网络接入点（Network Access Point，NAP）将任务卸载到基站、边缘服务器或者其他设备，这种卸载模式依赖于网络基础设施和云服务器等设施［6］，可能会带来一些问题：首先，随着对云服务需求的不断增加，这些设施需要频繁更新扩容和定期维护；其次，将计算工作负载卸载到云服务器会给移动用户带来数据通信和租用云服务的高昂成本［7］；最后，移动设备的互联网访问可能在某些区域不可用［8］，例如基站无法覆盖的森林、地下矿场等，这导致设备无法卸载计算任务。对于上述问题，一种解决方案是避免使用这些额外的设施，通过短距离无线网络接口将工作负载卸载到附近的移动设备，即D2D计算卸载［9］。

1 相关工作

在D2D 网络的计算卸载中，计算时延、计算能耗和任务成功率是重点关注的问题，已有许多国内外学者在这些方面进行了深度研究。

一个密集型应用可以拆分成若干的程序块并分配给不同的设备并行执行，以此缩短应用的执行时间。文献［10］提出了一种博弈论框架来减少无线D2D 网络中的任务执行时间。文献［7］将压缩视频文件的任务拆分并分配给附近的手机终端，减少视频压缩时间。文献［11］提出了一种启发式算法来最小化任务执行中的延迟。文献［12］提出了多维拍卖将任务分发到附近的设备，因此可以最大限度地减少延迟。

大量数据的处理会消耗过多能量，通过计算卸载可以有效减少能耗。为了最小化能耗，文献［13］提出一种基于稳定匹配的多用户计算卸载资源优化决策算法；文献［14］提出了图匹配；文献［15］提出了一个混合整数非线性规划问题；文献［16］提出了一种随机搜索算法；文献［17］提出了单维搜索。

任务成功率受设备移动性影响，为了提高成功率，文献［18］通过基于最佳响应动态算法获得多策略约束的纳什均衡；文献［19］采用多阶段随机规划方法来补偿不准确的移动性预测；文献［20］中通过考虑节点之间的社会关系并发现其联系模式中隐藏的规律。

上述文献关注的问题中存在时间和能量等多种量纲且相互制约的变量，这些变量大多通过权值进行分配，也有学者采用多目标优化进行处理。文献［21］将任务卸载至云服务器，提出了多目标优化问题，通过找到最优卸载概率和最优传输功率，以最小化能耗、执行延迟和价格成本。文献［22］提出了一种全局最优多目标任务卸载优化算法并基于Kuhn-Munkres算法进行求解。这些文献将任务卸载到云服务器，且很少考虑任务负载的划分。文献［23］基于粒子群优化的计算卸载算法，优化车辆边缘计算的延迟与成本多目标优化问题。文献［24］结合遗传算法和帕累托最优概念，提出了快速非支配遗传算法（NSGA-II），为处理多目标优化问题提供启发式的智能求解算法，许多学者将此算法应用于边缘计算的研究中。文献［25］改进NSGA-II 用于处理无线多热点网络的负载均衡，平衡网络吞吐量与设备选择接入AP的关系，但没有考虑最短时间与最小能耗的问题。文献［26］将NSGA-II应用于工作流应用程序的计算卸载，考虑将应用卸载到cloudlet和云。文献［27］提出基于NSGAII的卸载算法，节省了云机器人的能耗和程序执行时间。这2 篇文献都对时间、能耗进行了优化，但仍然依赖于远程云，存在远程服务设备不可用的风险，并且没有考虑设备移动性对任务成功率的影响。上述的文献将NSGA-II 应用在远程云服务的计算卸载研究中，但少有人考虑到网络设施不可用的情况，此时将任务卸载到附近的设备是更好的选择，因此，将NSGA-II 应用于D2D 网络计算卸载决策问题具有现实意义。

基于以上研究，本文的主要工作如下：

1）结合实际应用场景对问题建模，充分考虑设备和任务的异构性，设备的异构包括不同的计算能力、电池容量和随机移动性，任务的异构包括不同发布时间和不同的输入数据规模。

2）提出过度卸载的概念，分析过度卸载对执行时间、执行效率和错误处理的影响，并提出减少远程卸载数据量的方法。

3）基于NSGA-II算法，提出计算卸载算法，求出帕累托最优解集，对执行延迟目标和能耗目标进行优化。

4）提出数据路由算法（DRA），优化数据路由路线，平衡数据路由对路由节点的能耗。

2 系统模型

2.1 网络模型

图1展示了一个D2D 网络的场景，每个设备只能通过无线局域网进行交互，例如WiFi-Direct。在一个由N个移动设备组成的网络中，记I={ }1，2，…，N，每个移动设备都有有限的计算能力和电池能量，分别用RN和PN表示。设备以速度VN移动。如果设备j在距离dmax内，假设设备i可以直接与设备j连接，称设备j是设备i的邻居，邻居节点之间采用D2D 连接实现无线交互。网络中的设备分为2 类，当一个移动设备需要执行一项计算密集型任务时，称为任务设备（Task Device，TD），当一个设备处于空闲状态时，它可以与其他设备共享资源，称为资源设备（Resource Device，RD）。在不同时间点，每个设备都可以作为TD或者RD。

图1 D2D网络场景

2.2 任务模型

时间线可以切分为多个时隙，每一个时隙定义为t。在一个时隙内，每个设备都可能在不同的时间点产生一个任务，用二元组Ki={ }Di，Ci表示，其中i表示设备i，Di为任务数据大小（单位为bit），Di取自[Dmin，Dmax]，Ci为处理单位数据所需的CPU 周期。一个时隙内所有设备产生的任务的总数量m遵循泊松分布，m不会超过设备总量N。假设λ为任务的泊松分布到达率，定义为λ=kN，其中0≤k≤1。

2.3 移动模型

设备以速度VN随机移动，这可能导致RD 与TD断开连接，因此需要注意TD 与RD 的连接时间，确保数据传输和计算结果回传正常。假设每个设备都会记录一段时间内的位置，由此可以求出这段时间设备的平均速度VAvg。RD 的VAvg在卸载请求时已被TD 收集。TD 计算各个RD 的任务完成时间T，并根据VAvg求出T时刻各设备的位置，从而判断连接的可靠性。

2.4 时延模型

2.4.1 本地计算时延

TDi对Ki进行任务切分，Ki，i表示保留在TDi执行的部分，Ki，j(i≠j)表示传输到RDj执行部分，Ki，i的执行时间称为本地计算时延。每个设备维护一个任务队列，在同一时刻只执行一个任务。设τi，i为任务等待时间，为本地执行时延，则有：

其中，Di，i是分配给设备i的数据大小，Ri是设备i的计算能力。

2.4.2 数据发送时延

数据发送时延是指TD 发送数据块的时长。设为RDj接收TDi的数据块的结束时间，则有：

其中，为前一个设备接收数据块的结束时间，ρTx为传输速率；Hi，j为TDi到RDj的跳数，数据从一个设备发送到邻居设备称为一跳。

2.4.3 远程计算时延

在执行任务之前，RDj必须从TDi接收所有数据，在数据接收期间可以处理其他任务。若RDj数据接收完成时正在执行其他任务，则Ki，j加入任务队列并等待当前任务完成。令τi，j表示Ki，j服务等待时间，则Ki，j完成的时间记为：

2.4.4 结果回传时延

RDj在接收数据块后向TDi返回Ki，j的预计完成时间，TD根据这个时间的先后顺序向RD发送计算结果回传请求。RD 开始发送结果的时间有2 种情况：1）任务执行结束立即发送，RD 在任务执行结束之前收到结果返回请求，完成了任务的执行且无其他数据正在发送，此时可以立即回传计算结果；2）任务执行结束延迟发送，RD 在任务执行结束之后收到结果返回请求，无其他数据正在发送时返回计算结果。如果TDi收到RDj的计算结果，记为任务执行结束。令表示任务Ki，j执行结束时间，可由等式（4）得出：

其中，表示前一个设备的任务完成时间，ρRx是结果返回时的传输速度。

2.5 能量模型

2.5.1 任务执行能耗

任务执行能耗是设备执行任务产生的能耗。任务Ki，j的执行能耗由设备j的执行能量功率αj和计算时间决定。假设为任务Ki，j的执行能耗，表示为：

2.5.2 任务数据传输能耗

任务数据传输能耗是任务Ki，j进行数据发送和接收结果时产生的能耗。设和分别为设备n发送和接收1 bit 数据所需要的能耗。对于任务Ki，i，由于是在TDi本地执行，它的任务数据传输能耗为0。对于任务Ki，j(i≠j)，它的数据传输可能为一跳或者多跳。令＜a，b＞( )a，b∈I表示设备a到设备b的单跳传输过程，e＜a，b＞为传输能耗系数，表示为：

当Ki，j从TDi经过一跳到达RDj时，任务数据传输能耗可表示为：

当Ki，j经过多跳到达RDj时，假设k={k1，k2，…，kl}(k1，…，kl∈I)表示从TDi到达RDj的中继设备集合，此时，Ki，j从设备i经过设备集合k到设备j的传输过程表示为＜i，k，j＞。由于多跳传输过程可以视为多个一跳传输过程之和，传输过程＜i，k，j＞可以拆分为＜i，k1＞，＜k1，k2＞，…，＜kl-1，kl＞，＜kl，j＞。因此，多跳任务数据传输能耗可表示为：

3 过度卸载

根据卸载到远程设备的数据量，计算卸载可以分为完全卸载和部分卸载。对于完全卸载，一个任务的结束时间取决于所有远程执行任务的计算结果返回时间。而对于部分卸载，除了远程执行的任务之外，还需要注意本地执行的任务。通常，当TD 产生计算密集型任务时，它倾向于将尽可能多的数据卸载到RD，这可能会卸载过多的数据，称为过度卸载（定义1）。过度卸载在资源浪费和卸载超时2 个方面影响计算卸载的效率，本文将通过图2 和图3 进行详细分析，其中节点1为TD，其他结点为RD。

图2 过度卸载

图3 无过度卸载

定义1过度卸载。假设进行计算卸载的设备为TDi，最后一个返回计算结果的设备为RDn，(i，n∈I，i≠n)，当时，称TDi存在过度卸载。

3.1 资源浪费

TD 过度卸载会导致资源浪费，主要表现在3 个方面：

1）TD 计算资源的浪费。由于远小于，TD 过快进入空闲状态，导致其计算资源无法有效利用。如图2 所示，t0是TD 上本地执行任务的完成时间，而t2是最后一个RD 结果回传的结束时间，可见TD在t0到t2时间内处于空闲状态。

2）卸载大量数据会占据网络资源。当数据量较大时，传输时间较长，这可能导致网络堵塞。

3）由于RD 需要接收所有数据后才能进行计算，当过大的数据传输会导致RD 长时间处于接收状态而无法提供有效的卸载服务。

3.2 卸载超时

卸载过程中可能出现设备掉线、任务执行错误等情况，TD 需要及时做出处理，否则可能出现卸载方案比本地执行方案使用更长的执行时间的情况。如图2 所示，考虑最坏情况，TD 在发送所有数据之后（t1时刻）无法接收所有RD 的执行结果，并需要在本地执行未完成的子任务。由于TD 在t0到t1之间处于空闲状态，它需要在t2之后继续执行t1-t0时长，可见进行卸载时的总执行时间比不进行卸载时的总执行时间长，即卸载超时。

3.3 问题解决

对于处理过度卸载，最有效的办法是限制卸载数据的大小，保证TD 在整个卸载过程中不处于空闲状态。此时，TD的本地计算时延大于最后一个RD的任务执行结束时间。假设最后一个返回计算结果的设备为RDn，则有

如图3 所示，在无过度卸载场景下，TD 保留更多的数据在本地执行，从而减少了网络传输以及RD 执行任务的时间。计算卸载的结束时间从RD 结果回传的结束时间t2缩短到TD上执行任务的结束时间t'0，因此无过度卸载要比过度卸载有更高的计算卸载效率和资源利用率。另外，TD 作为最后一个完成子任务的设备，可以及时发现存在的卸载失败并进行处理。TD 可以在t'0之前检测到卸载失败，并将失败的子任务加在当前执行任务之后，实现子任务无缝切换（任务的切换时间忽略不计），在最差的情况下，所有子任务都在TD 上执行，总执行时间等于本地执行方案的总执行时间，这有效防止了卸载超时的发生。

4 问题形式化与算法

TD（ii∈I）在一个时间周期t内随机产生一个任务，记为Ki={Di，Ci}，该任务需要消耗大量的执行时间和能量。TDi的附近存在空闲的RD（ji∈I，j≠i），它们可以为TDi提供计算资源。TDi产生一个任务后广播其卸载请求，RDj收到请求后，回复自己的设备状态。TDi在收集到RDj的响应之后将Ki划分为子任务Ki，j={Di，j，Ci}，其中Di，j≤Di，并做出卸载的决定，称为卸载决策问题。本文将卸载决策问题转化为求解多目标最优解问题，该问题包括任务执行时间最小化问题以及卸载能耗最小化问题。设卸载决策问题的最优决策为X，它可以表示为下列的决策向量：

其中，X的每一列表示TD的对RDj的卸载决策，表示形式为百分比，xi，n表示最后一个设备n的卸载决策。因此，Ki，j也可以表示为Ki，j={xi，jDi，Ci}。

4.1 多目标函数

由第2节、第3节的分析可知，卸载的完成时间是TD对计算结果接收完成的时间，包括接收RD远程计算结果的时间以及本地处理数据的时间，定义为：

总能耗等于任务执行能耗和任务数据传输能耗之和，定义为：

则多目标函数F（x）表示为：

卸载决策问题转化为求解多目标最优解问题，可由下式给出：

其中，式（15）解决过度卸载问题；式（16）表示任务Ki，j消耗的能量不能高于RDj的剩余能量；式（17）表示RDj分配的数据量应大于最小执行数据量；式（18）表示各个设备数据分配的权重之和为1；式（19）表示RDj在(xi，j)时刻与TDi断开连接的概率应小于。如图4所示，令为TDi在时刻的位置，为RDj响应卸载请求时的位置，则RDj在之前的移动范围为以为圆心半径为rj的圆形区域，其中rj为平均移动距离。当RDj移动出TDi的通信范围外，即S区域时，将其视为RDj掉线，此时无法进行数据传输。因此，RDj的掉线概率为：

图4 RDj掉线区域

由于多目标优化中存在多个目标函数，并且它们的量纲不一致，对于可行解集的解，无法用传统的等于、大于或小于等数量关系进行优劣关系的比较和排序，需要用另外一种关系来定义2 个可行解的优劣关系，称为帕累托支配（Pareto Domination），又称帕累托占优。设xA，xB∈X是公式（14）的2 个可行解，则称与xB相比，xA是帕累托占优的，当且仅当：∀i=1，2，…，F（ixA）≤F（xB）且至少存在一个j∈{1 ，2，…，m}，使得Fj（xA）＜F（xB），则称xA支配xB，记为xA≺xB。帕累托最优解（或非支配解）可以表述为可行解xA∈X，当且仅当：∄x∈X，使得x≺xA。

因此公式（14）的解以帕累托最优解的集合构成，称为帕累托最优解集，定义如下：

4.2 计算卸载决策算法

基于NSGA-II，本文提出计算卸载决策算法。首先，算法根据RD 的计算能力和任务队列信息求得任务Ki，j的服务等待时间τi，j并将RD 进行排序得到发送队列顺序，这可以有效减少任务Ki，j的执行时间；其次，算法根据设备的位置、平均速度、计算能力、能耗系数和任务队列等设备信息求得目标函数值；最后，算法提出适用于计算卸载的基因编码、交叉和变异方法。

4.2.1 编码

传统的遗传算法的基因编码包括二进制编码、符号编码和实数编码等，在本文中，计算卸载问题的解表示为各个设备分配数据量的百分比，因此基因值应该为［0，1］区间的浮点数，且所有基因值之和等于1，这可以由一组随机数除以它们的均值得到。假设多目标问题的解为n维向量Xf=[x1，…，xn]，n维随机数组U=[u1，…，un]，则基因编码可由下式得到：

4.2.2 交叉

在卸载决策场景中，每个基因表示分配数据的比例，2 个个体基因的简单交换会改变其他基因所占有的比重，无法保持父代的性状。因此基因的交换并不是交换基因编码，而是交换多个随机位置上所占基因的比例。如图5 所示，设父代1 和父代2 为进行基因交叉的个体，总共有8 个基因位点，其中假设父代2 的4 和6 位点被父代1 替换，且a4+a6≠b4+b6，则子代的基因编码之和不等于1，并且子代无法保留父代2的性状。令A和B分别为父代1和父代2替换位点基因值组成的集合，A=［a1，…，an］，b=［b1，…，bn］，则子代交叉生成的基因值由下式给出：

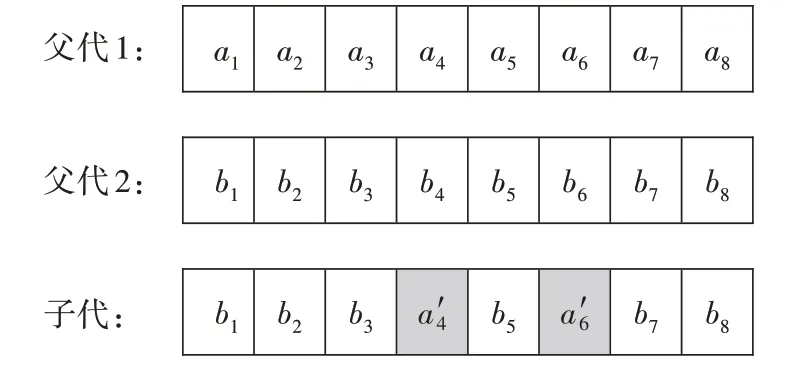
图5 交叉

4.2.3 变异

如图6 所示，个体在4 和6 号位点发生变异，需要满足b'4+b'6=b4+b6。假设n维变异位点集合B=[b1，…，bn]，n维随机数组V=[v1，…，vn]，满足变异后的位点集合为B'=[b'1，…，b'n]，则b'i可表示为：

图6 变异

4.3 数据路由算法

得到卸载决策后，TD通过D2D无线链路向RD发送数据，为此，本文提出了数据路由算法（Data Routing Algorithms，DRA）。首先，数据传输需要确定路由表。如果RD 在TD 的通信范围内，则可以直接传输，记这些节点为RDin，如图7（a）中的节点1、2 和3。对于TD的通信范围之外的RD，数据传输需要路由节点，这些节点记为RDout，如节点4、5、6和7。令Aj表示RDin的集合，其中RDin表示RDout和TD 的共同邻居，数据可以通过Aj进行路由。任何一个RDin都应该尽可能地协助完成数据路由，单一节点不能实现数据块的并行传输，并且可能会过快消耗路由节点的能量。记RCi为RDin转发数据块的计数，RDoutj选择RCi最小的RDini作为下一跳路由节点，然后RCj加1，直到存在TD 与RDoutj的路径Pj。之后，数据块的发送需要确定顺序，以减少数据传输碰撞。基于路由表，可以得到图7（b）所示的路径有向图，它最终转化为一个传输队列Sq。首先，对节点0 上的3 棵子树分别进行前序遍历，得到队列1、2 和3（Sq1、Sq2和Sq3）；之后，取Sq1的队首压入Sq；然后，依次取Sq1、Sq2和Sq3的队首压入Sq，直到所有队列为空。DRA如算法1所示。

图7 节点位置和路径有向图

算法1数据路由算法

输入：TD，RD

输出：Sq

1 RDin←{v|v∈RD，v在TD范围内}；

2 RDout←{v|v∈RD，v不在TD范围内}；

3Aj←{v|v∈RDin，v为TD和的共同邻居节点}；

5 whilePj=Φ

6 在Aj中取最小RCi的节点RDini作为下一跳节点；

7 RCi加1；

8 end

9 end

10 创建路径有向图T0，设T1，…，Tk为T0的k棵子树；

11 foreachTkdo

12 Sqk←对Tk进行前序遍历；

13 end

14 将Sq1队首压入Sq；

15 while Sq1，…，Sqk≠Φ do

16 foreach Sqkdo

17 将Sqk队首压入Sq；

18 end

19 end

5 性能评估

本文在NS-3 上模拟无线通信网络的传输，实验场景由10 个移动节点组成，它们随机分布在一个50 m×50 m 的平面空间中，以［1，3］m/s 的速度在不同方向上进行均匀的移动，并且可以在某个点改变方向。在通信范围R=40 m 的范围内，2 个移动设备通过WiFi-Direct 连接。在一个任务产生周期t=120 s 内，所有设备都随机产生任务，任务总数量遵循泊松分布（λ=0.25）。每个设备都有计算能力，为了更加直观地表示数据量与计算能力的关系，本文将计算能力的单位转化为kbit/s，设备的计算能力的大小遵循高斯分布，其中μ=1024×1.0，σ2=（1024×0.4）2。通过计算卸载算法求得时间最优分配（Time Optimal Allocation，TOA）以 及 能 量 最 优（Energy Optimal Allocation，EOA），并与以下基线方案进行比较，分析数值结果评估所提出算法的性能：

1）本地计算（Local Computing，LC）：TD 生成的数据仅在本地执行，不进行计算卸载。

2）平均分配（Equal Allocation，EA）：TD 根据可卸载设备数量平均划分数据。

3）计算能力分配（Computing Power Allocation，CPA）：TD 根据可卸载设备的计算能力作为权重进行数据划分。

5.1 平均执行时间

图8 显示了任务数据大小对平均执行时间的影响。当数据量小于10 MB 时，所有卸载方案都会选择本地执行。当数据量在［10，40］MB之间时，所有卸载方案的平均执行时间都以平稳的趋势上升，其中CPA、TOA 和EOA 的平均执行时间都要比EA 少。当数据量大于40 MB 时，TOA 偏向于执行时间的最小化，所以平均执行时间比其他的卸载方案更少；而EA的平均执行时间最长；相对于其他3 种方案，CPA 是最不稳定的，因为当TD计算能力较弱时，CPA会选择卸载更多的数据，而卸载数据量较大时，会产生网络拥堵，增加传输时间。综上所述，在数据量较少时，所有卸载方案的平均执行时间基本一致；当数据量较大时，TOA相对其他卸载方案能得到最小的平均执行时间。在稳定性方面，TOA、EOA和EA平均执行时间变化较为稳定，而CPA受网络影响较大。

图8 平均执行时间

5.2 平均提升效率

提升效率是一个任务节省的时间与本地执行时间的比值，而平均提升效率是所有任务的提升效率的平均值。图9 是任务数据大小对平均提升效率的影响。当数据量在［20，40］MB 时，TOA、EOA 和CPA 都在20 MB 时迅速达到较高的水平，之后缓慢提升。CPA 的平均提升效率要比EOA 高，这说明在数据量较少的时候，根据计算能力进行数据划分能得到较好的提升效果。EA 则是稳定缓慢提升，可见根据设备的不同状态进行数据划分更能有效提升计算效率。在40 MB 时，所有的卸载方案的平均提升效率都达到峰值，其中TOA 为41.7%，EOA 为37.2%，高于其他方案。当数据量大于40 MB 时，所有卸载方案的平均提升效率开始下降。TOA 和EOA 在80 MB 之后趋于平衡，TOA 收敛于31.8%，EOA 收敛于26.8%。EA和CPA 下降非常迅速，收敛值均在21%左右。因此，TOA 和EOA 进行计算卸载的平均提升效率明显比EA和CPA稳定，且TOA能取得较好的提升效率。

图9 平均提升效率

5.3 卸载数据量

图10 对比了不同卸载方案向附近RD 卸载数据的数据大小的区别。EA卸载的数据量呈现线性上升趋势，与响应卸载请求的RD 数量成正比。CPA 根据计算能力大小进行数据划分，计算能力较强的设备将处理更多的数据，而计算能力较弱的设备将分配更少的数据。在数据量小于70 MB 时，CPA 方案卸载的数据量要多于EA 方案。对于TOA 和EOA，卸载的数据量要明显低于其他方案，节约了能耗成本，同时也节约了网络资源。当数据量在［20，40］MB 之间时，TOA 和EOA 卸载的数据量基本相同，在40 MB 之后，EOA 的卸载数据量要明显低于TOA。这是因为计算卸载算法考虑了过度卸载问题，对卸载的数据量进行限制，节约了数据传输的时间。

图10 卸载数据量

5.4 卸载对象选择对能耗的影响

图11对比了不同卸载方案的能量消耗情况。EA方案的能耗明显高于其他方案。TOA、EOA 和CPA在40 MB 之前的能耗大体一致，而在40 MB 之后，EOA 要明显低于其他方案，这主要包括2 方面原因。1）卸载数据量较少。如图10 所示，EOA 卸载的数据量明显少于其他方案，这减少了传输能耗。2）卸载对象的选择。图12 展现各个卸载方案生成的子任务数量，EOA 会选择将任务卸载到计算能力较强的设备，淘汰计算能力较弱的设备，从而节省能量，TOA 则是尽可能利用空闲的RD 进行任务卸载，这样可以获得更多的时间效益，但也比EOA消耗更多的能量。CPA和EA 并不考虑时间效益和能耗效益，而是尽可能多地将数据发送到附近的RD 进行处理，导致消耗更多的数据传输时间和数据传输能量。

图11 能耗

图12 子任务总数量与重传子任务数量

5.5 子任务重传率

子任务重传率是重传子任务总量与子任务总量的比值，它代表了卸载方案的可靠性。如图12 所示，EOA、TOA、CPA 和EA 的子任务重传率分别为9.3%、7.8%、22.6%和17.3%，可见EOA 和TOA 要明显优于CPA 和EA。这得益于2 个方面原因：1）对于过度卸载的处理，限制了卸载的数据量，有效防止了网络堵塞；2）对设备掉线率的考虑，TOA 和EOA 在进行卸载对象的选择时，考虑了设备连接性，这有效提高了任务卸载的成功率。

6 结束语

本文研究了移动边缘计算中D2D 网络的计算卸载问题，将该问题转化为多目标优化问题，并提出了一种计算卸载算法求解时间最优解和能量最优解。另外，本文提出了过度卸载的概念，分析过度卸载对于部分卸载的不利影响并提出解决方案，限制TD 的卸载数据量，有效提高TD 的资源利用率并解决卸载超时问题。在模拟实验中，本文将所提出算法与基准卸载方案进行比较，在不同的场景下评估算法的效率。实验结果表明，在提升效率方面，各个卸载方案在数据量为40 MB 时可以达到最高的平均提升效率，其中TOA 远高于其他方案，并且当数据量增大后，TOA 也能有较好的平均提升效率；在能耗方面，EOA 可以节省更多能耗；在数据传输量方面，TOA 和EOA 能有效减少数据传输量，有效减少网络拥堵；在任务重传率方面，TOA 和EOA 能够有效减少数据传输错误的情况。