基于无模型自适应控制的视觉伺服

彭宗玉，黄开启，苏建华，王丽丽

（1.江西理工大学电气工程与自动化学院，江西 赣州 341000；2.中国科学院自动化研究所复杂系统与智能科学国家重点实验室，北京 100190）

0 引 言

机器人在视觉引导下跟踪并抓取目标物体是智能制造和航天探索中的一项重要任务。例如在生产线上，利用机器人快速识别并精确抓取传送带上快速移动的物体，能够提高生产效率；在航天领域中，利用空间机械臂捕获空间碎片，能够避免碎片碰撞航天器，保证航天器与宇航员的安全。机器人视觉伺服控制方法利用视觉反馈得到的数据来控制机器人的移动，成为机器人在非结构化环境中抓取或操作目标的主要技术。从现有的文献资料来看，机器人视觉伺服跟踪方法主要有3 类［1-4］：基于位置的视觉伺服（PBVS）、基于图像的视觉伺服（IBVS）和混合视觉伺服（HBVS）。PBVS利用位姿误差作为系统输入量，需要对目标的位姿进行准确预估，并且依赖于系统参数的精确标定；IBVS 由于避免了对相机外参数的标定、机器人手-眼系统标定等步骤，系统结构也更为简单，因此这种方法成为近年来研究人员关注的热点；HBVS 虽然结合了以上2 种方法的优点，但控制器相对复杂。此外，相机的固定方式有2 种：1）相机固定在空间中的某一固定位置（eye-to-hand），这种固定方式需要精确标定相机内外参数；2）相机固定在机械臂末端（eye-in-hand），相机跟随机械臂的运动，相机与定位目标之间的位置始终在变化，可以更精确定位目标。本文则采用了eye-in-hand方式。

IBVS 方法虽然避免了标定相机参数过程，但需要准确计算机器人手-眼系统的雅可比伪逆或逆矩阵，并且伺服控制器的性能与雅可比矩阵的精度密切相关，因而如何快速、精确地在线识别图像雅可比矩阵是视觉伺服中需要解决的重要问题之一。Zhang等人［5］基于递归神经网络设计了机器人视觉伺服神经网络控制器，避免了对雅各比进行求逆运算。Jiang等人［6］使用数据驱动的非虚化控制器实现视觉伺服控制，其中通过将图像特征与3D 模型相匹配来识别目标。但是，雅各比矩阵的奇异点或是外部扰动导致的参数变化会影响机器人伺服控制器的稳定性和精度。黄正军等人［7］提出了一种基于图像轨迹规划与时序控制相结合的视觉伺服方法，采用卡尔曼滤波器估算目标与相机相对位姿，通过结合相机测量实现了雅可比矩阵的自适应估计。Wu等人［8］则利用在线估计和卡尔曼滤波的方法估计图像和关节雅各比矩阵，同样也避免了求解雅各比矩阵的伪逆，但需要通过多次采集图像和运动数据得到初始的雅各比矩阵。

针对机器人的跟踪误差问题，研究人员也进行了大量的研究。例如刘珊等人［9］设计了一种基于逆向运动学补偿的滑模控制算法，以保证轨迹跟踪误差能够在较短时间内收敛；Tomei 等人［10］提出了一种鲁棒自适应控制方法，该方法通过对摩擦力进行补偿，能够在系统存在未知有界扰动及摩擦力情况下，有效解决轨迹跟踪问题。杨亮等人［11］提出了一种自抗扰控制器，利用扩张状态观测器对扰动进行观测并补偿，提高了系统的抗扰性能。Lee 等人［12］则将机器人的动力学与运动学都考虑在系统中，结合模糊滑膜控制方法，提高了视觉伺服系统的动态性能。虽然机器人轨迹跟踪控制已经取得不错的效果，但上述文献的控制方案均建立在机器人动力学模型准确已知的基础之上。陈梅等人［13］提出了以图像特征为反馈的模糊控制策略，通过对机器人的动作状态进行控制，实时反馈图像信息，纠正系统模型误差。近年来，随着强化学习的兴起，在视觉伺服中利用强化的方法进行优化已有较多先例，文献［14-16］均采用强化学习方法来提高视觉伺服的性能，Tan 等人［14］利用递归神经网络在机器人参数不确定的情况下提高了视觉伺服的跟踪响应速度和精度；Ye 等人［15］利用Q 学习和深度Q 网络相结合的方法提高了系统的跟踪精度；Tan 等人［16］利用归零神经网络方法提高了在不需要机器人参数的先验知识的情况下视觉伺服跟踪的鲁棒性。但这一类方法需要大量的数据进行训练，训练过程耗费大量时间，建立的强化学习模型准确性与数据量相关性较高。

在视觉伺服控制系统中，系统在长时间运行过程中由于受到磨损、冲击等原因会导致系统参数变化，从而导致系统模型发生变化，并且会进一步导致跟踪误差增大。本文主要参考文献［17］所提出的无模型自适应控制方法（MFAC），利用输入输出数据在线估计机器人参数和图像雅各比矩阵，以有效应对系统参数变化导致的参数扰动问题，在不需要对视觉伺服控制系统的干扰进行分析建模的情况下提高系统的鲁棒性。通过仿真与实体实验验证，该方法能够在系统模型存在扰动的情况下提高视觉伺服控制的定位精度，且能够提高系统收敛速度。

1 问题描述

本文研究的基于图像的视觉伺服控制系统如图1、图2 所示，系统中相机固定方式为eye-in-hand，即相机固定在机械臂末端。相机采集图像后提取定位板上特征点位置，与期望特征点位置进行对比，得到的误差输入到控制器中，控制器则输出各个关节速度，机器人伺服系统则控制机器人的各个关节速度，使得机械臂末端带动相机一起运动，让图像特征点位置最终到达期望位置。

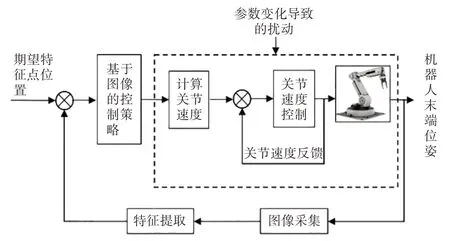
图1 系统模型

图2 实验场景

假设目标物体特征点在图像物理坐标系下的坐标是f=（x，y）T，对应的速度是用r=（Xc，Yc，Zc，θx，θy，θz）T表示相机的姿态，则速度为ṙ=（Tx，Ty，Tz，ωx，ωy，ωz）T，其中v=（Tx，Ty，Tz）表示平移速度，ω=（ωx，ωy，ωz）表示角速度。特征点ri与其投影点fi之间的位置关系为［15］：

其中，λ表示相机的焦距。相机坐标系下特征点的速度与图像物理坐标系下特征点速度之间的关系如下：

其中Jri表示图像雅可比矩阵，该矩阵定义了图像物理坐标系下的特征点速度与相机在笛卡尔空间的速度之间的关系［16］，形式如下：

在视觉伺服控制过程中还涉及机器人的关节速度控制，机械人动力学方程描述了机械人关节速度与机械人末端位姿的速度关系，方程为：

其中，Jq为机械人雅各比矩阵，Jq∈R6×n；̇为n自由度的机器人关节速度矢量；由于相机固定在机器的末端̇既表示相机的速度也表示机器人的末端的速度。

在长期运行过程中机器人受到各种干扰影响，模型参数通常会发生变化，产生的扰动为Jn，从而影响系统定位精度和定位速度。由于机器人参数改变，导致建立的机器人模型不准确。本文考虑到扰动，定义机器人的雅各比矩阵为：

其中，Jqr为期望的机器人雅各比矩阵。

将式（4）代入式（2），可得：

其中，J+q为机器人雅各比矩阵的伪逆，J+r为图像雅各比矩阵的伪逆。在控制过程中机器人受到的扰动对视觉伺服跟踪过程始终产生影响，尽管图像特征点位置可由准确计算得到，但是误差依然会存在。

2 基于MAFC视觉伺服

2.1 MFAC原理

建立受控系统的数学模型并非易事，并且数学模型一般对系统进行简化，即无法准确估计系统的动态变化。无模型自适应控制则仅利用系统的输入输出数据进行控制，控制过程中不需要建立受控过程的准确数学模型［17］。

引入多输入多输出系统的MFAC方法［18-23］，考虑如下系统：

其中，u(k)∈Rm、y(k) ∈Rm分别表示k时刻的系统输入与输出，nu、ny是2个位置正整数。当该系统满足以下2 个条件时，即得到期望的雅各比矩阵，在运行过程中实时计算，每个执行周期内都利用期望的雅各比矩阵进行控制。

条件1：f（k），k=1，…，m，关于第（ny+2）个变量的每个分量都具有连续的偏导数。

条件2：系统中满足对任意的k1≠k2，k1，k2＞0，u（k1）≠u（k2），则：

其中，y（ki+1）=f（y（ki），…，y（ki-ny），u（ki），…，u（kinu））；i=1，2；b＞0为常数。

当‖ Δu（k）‖≠0时存在一个矩阵伪偏导数Φ（ck）∈Rm×n，可以将系统式（8）简写为：

并且该系统的估计准则函数为：

其中μ＞0为权重因子的期望。

系统式（7）满足上述系统条件，其紧凑型线性化形式如下：

其中，α与c均为比例系数，且都大于0。

2.2 控制器设计

假设通过特征提取算法获得m（m＞3）个特征点fi（i=1，2，…，m），假 设 期 望 的 特 征 点 位 置 是(i= 1，…，m)，相应速度是(i= 1，…，m)，定义视觉跟踪的位置误差和速度误差为：

引入滑模控制方法［24-28］：

其中Kp＞0，若系统收敛则s（t）=0。设计如下控制率：

其中Ks＞0，为饱和函数比例系数，饱和函数如下：

3 实验验证

3.1 仿真实验

为了验证上述方法的有效性，本文在仿真软件中进行了实验验证。实验环境如图2 所示，其中包括：UR5 机械臂、相机、定位板。机械臂的各个关节角度、角速度、角加速度都可以精确控制，机械臂的DH 参数如表1 所示，2~5 列参数分别为连杆长度、连杆扭转角、关节转角、连杆偏距，其中机械臂在初始时末端竖直朝下。相机的分辨率为1280×720，其固定在机械臂的末端，也是竖直朝下，相机的图像数据可以通过仿真软件接口实时获取得到。定位板长宽都为20 cm，上面有4 块不同颜色的小方块，分别位于定位板的4 个角，颜色块的中心点在图像中位置通过颜色识别算法提取得到，各个色块在图像中期望位置如表2 所示，u表示为横向像素点位置，v表示纵向像素点位置。

表1 UR5机械臂DH参数

表2 期望特征点位置/像素点

实验利用Pycharm 软件实现上述控制算法，图像处理算法实时与仿真软件进行交互，实时获取图像并处理分析，计算得到机器人关节速度，并将机器人的关节速度输入到仿真系统中，从而实现对仿真环境中的机械臂实时控制。实验的控制周期为100 ms，实验持续时间为100个周期。

实验分为2 组，其中一组是利用MFAC 方法，即按照式（18）进行控制，另一组则是不采用MFAC 方法进行控制，其表示为：

在实验中为了模拟干扰，在2 组实验中的雅各比矩阵计算过程中都添加了随机的白噪声Jn。

实验中的平均误差通过如下方法求取：

其中，n表示特征点的个数，n=4。总的误差均值则是按照如下公式计算：

其中，t为周期数，实验中t均等于100。

图3 为实验采集到的初始图像，实验初始时定位板在图像的右上角，且定位板在图像中的角度也是偏转的。图4 为相机采集到的最终图像，定位结束后定位板处于了图像中心，定位板边位于图像中心。2 种实验方法的图像情况基本一致，无法通过肉眼观察到其中的区别。

图3 相机初始图像

图4 相机采集最终图像

图5 显示的是2 种方法实验结果的误差均值曲线，2 种方法基本都在2 s 内收敛到了期望特征点附近，其中未采用无模型自适应控制的方法收敛速度明显更慢，误差也出现一定的波动。

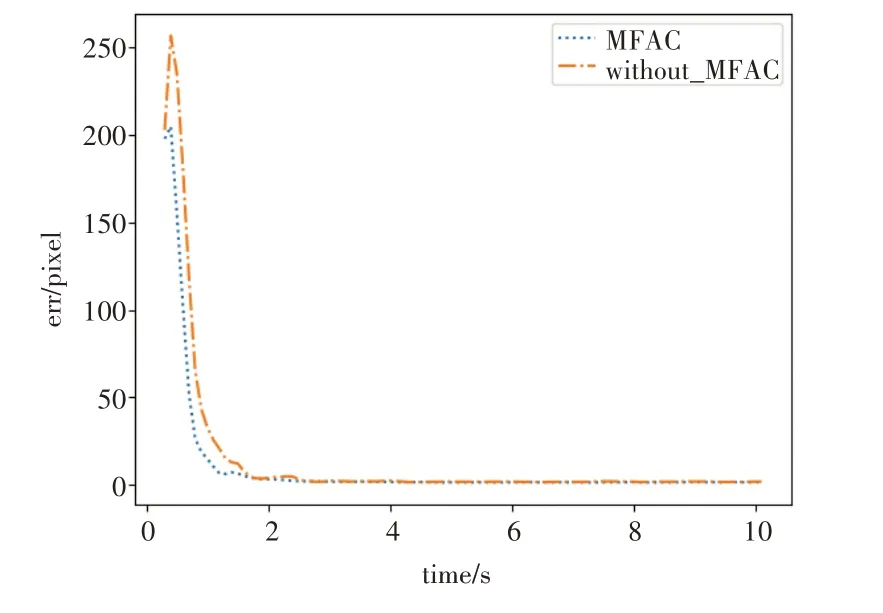
图5 误差均值曲线图

图6 与图7 显示的是2 种方法的特征点在图像中的轨迹。图中灰色的方框为定位板在图像中的初始位置，黑色方框则为最终的位置。对比可以看出，采用MFAC 方法后特征点在图像中的轨迹更加平滑，同时到达期望的特征点也更加迅速。表3所示的是2种方法各特征点在u和v轴上的最终误差，对比可以看出采用MFAC方法后，视觉伺服误差更小一些。

表3 各特征点最终误差/像素点

图6 未采用MFAC方法的特征点轨迹

图7 采用MFAC方法的特征点轨迹

此外，为了避免由随机噪声在不同实验中差异性所导致的偶然性结果，本文还进行了多次实验，每次将实验定位板摆放于不同的位置，即定位板在图像中的初始位置发生改变，但特征点的期望值始终不变，分别用2种方法进行测试，实验数据如表4所示。

表4 多次实验结果/像素点

以上多次实验结果表明，未采用MFAC 方法的最终均值误差与总的平均误差均比采用MFAC 方法更大一些。因此上述仿真实验结果能够验证本文提出的MAFC 方法能够提高视觉伺服系统应对参数干扰问题的能力。

3.2 实体实验

为了验证上述方法在物理世界中真实可行，本文还进行了实体实验，实验硬件系统如图8 所示，同样采用UR5 机械臂进行实验，实验中采用大恒图像公司的MER-041-436U3M 灰度相机，分辨率为720×540。实验中采用的定位板是一块黑色方块，上面贴有二维码，通过对二维码的分析可以得到这个二维码的4 个角点在图像中的位置，即图像特征点。采用与仿真实验相同的编程软件与控制算法，图像识别算法则改变成了对二维码的识别，识别后处理得到二维码的角点位置，控制过程同样对机械臂关节速度进行控制。控制周期在硬件条件允许的情况下达到了50 ms，周期设置为200，整个实验时间总长为10 s与仿真实验一致。

图8 实体实验环境

相机采集到的初始图像如图9 所示，定位块初始时位于图像的左上角，二维码的4 个角点以及中心点都通过图像处理标记为了白色的圆点。采集到的最终图像如图10所示，2种方法最终定位结果都趋近于期望的特征点，通过肉眼无法观察得到2 种方法的最终误差。

图9 相机采集的初始图像

图10 相机采集的最终图像

实验中特征点的轨迹如图11与图12所示，2组图中位于左下角的黑色虚线矩形框为定位块在图像中的初始位置，黑色实线框则是最终定位块在图像中的位置。图11未采用MFAC方法，可以比较明显地看出轨迹波动较大，而图12所示的轨迹明显更加平滑，2种方法结果都在靠近最终的期望位置时有些微小变化。

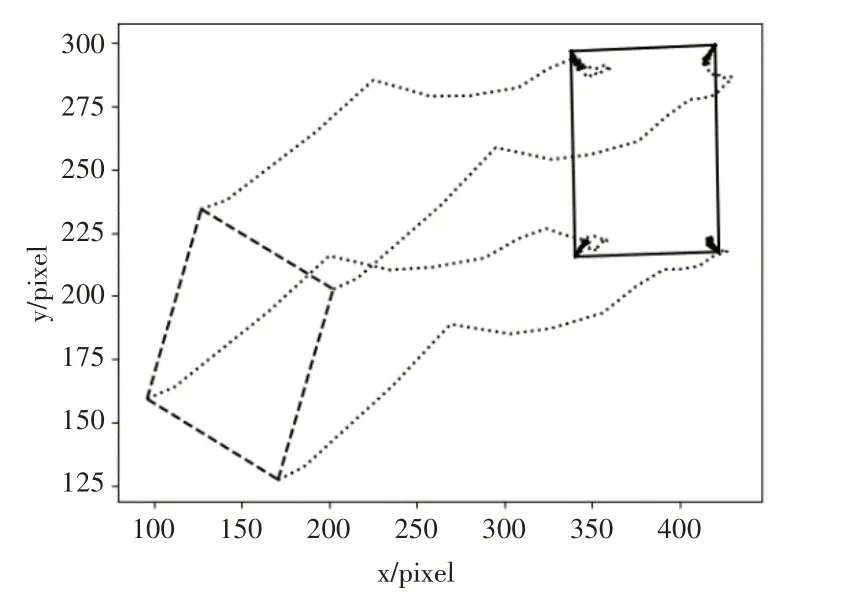
图11 未采用MFAC时特征点轨迹

图12 采用MFAC时特征点轨迹

表5 所示的是2 种方法各个特征点的u和v轴方向的最终误差，对比可以看出采用MFAC 方法的各特征点误差略小一些。图13为2种方法的平均误差变化折线图，误差趋近于零更慢的是未采用MFAC方法。

表5 实体实验特征点误差/像素点

图13 2种方法平均误差对比图

实体实验结果表明，采用MFAC方法的视觉伺服控制在应对参数扰动的情况下，对比不采用该方法，能够提高系统的收敛速度和定位精度。与仿真实验对比，2种实验结果基本一致，实体实验由于控制周期的减小，图像特征点轨迹也显现出更加平滑，控制周期数量的改变也使得定位误差相比于仿真实验也更小一些。

4 结束语

本文针对基于图像的视觉伺服中系统参数扰动问题，采用无模型自适应控制方法，避免了对系统各种扰动的精确建模分析，将机器人雅各比矩阵与图像雅各比矩阵进行在线更新修正，并利用滑模控制方法，使系统收敛速度加快。通过多个对比实验验证，实验结果表明，此方法能够有效提高视觉伺服系统应对参数扰动问题的能力，并且使得系统能够将最终定位误差减小。此外实验过程中机器人的运行也更加平滑，有助于保护机器人，避免受到过多冲击。