一种面向城市战场的智能车自主导航方法

李 鹏，徐 珞

（中国电科智能科技研究院，北京 100005）

0 引 言

随着城市化程度的不断增加，城市地区的安全问题也变得愈发严峻。城市作为军事行动和社会治安的主要场所，战场突防能力的强弱决定着我方能否快速地占领敌方据点或制高点，掌握战场主动权。当突防任务需要穿越城市区域时，密集的建筑群、复杂的交通情况以及未知的敌方拦截使得完成任务的难度大大增加。同时在实际的行动中人为地提前规划突防路线，不仅依赖精确导航地图，同时还难以应对各种突发状况，像躲避突然出现的车辆、敌方单位或行人等。因此针对该情况，需要一种实时、高效和智能的路径规划方法协助完成突防任务。

传统的路径规划算法虽然能够解决部分路径规划问题，但是在城市战场环境下往往无法胜任。例如A*算法［1］和Dijkstra 算法［2］都是基于图论的全局路径规划算法，二者虽然对于路径的求解过程有所区别，但在具有精确地图的情况下都具有不错的性能和准确度，因此其在海战战场、路由规划和导航系统等场景中具有广泛应用。而面对城市战场时，如图1 所示的2类代价地图难以获取，因此A*算法和Dijkstra 算法在该场景不具有可行性。

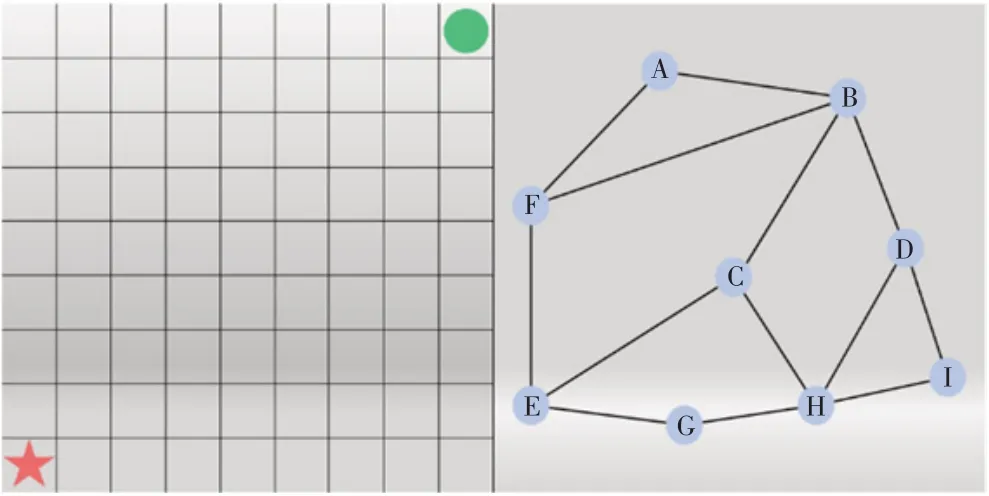
图1 路径规划代价地图

此外随机路线图算法（PRM）［3］和快速扩展随机数（RRT）算法［4］也需要通过采样的方式基于已知的地图数据建立无向图，且采样点过少、噪声干扰、局部最优和不合理的参数设置均可能导致找不到可行的路径解。智能仿生类算法如蚁群算法、遗传算法、粒子群算法等［5-7］，虽然对于多数任务和环境具有不错的实用性，但这类算法评价函数的计算需要全局地图的辅助，且其迭代过程具有很大的随机性，因此这类算法的收敛速度无法估计且规划时间相对较长，被广泛应用于一些能够离线规划的任务如快递配送路线规划和作战方案优化等。综上所述，全局规划类的算法由于需要构建已知的全局地图，且各类算法均有自身的局限性，因此在面对三维城市战场环境时并不能很好地适用。

人工态势场法［8-9］作为一种局部路径规划算法，其基本思路是通过叠加障碍物周围的斥力和目的地周围的引力构建一个势力场，使物体沿着势能按由高到低的方向移动。然而，在面对三维城市战场中的不规则物体时，该算法的势力场构建十分困难，即使在面对二维环境中的不规则障碍物时，其势力场构建也需要大量的计算。谌海云等［8］将其应用于无人机的三维编队问题，但其任务场景中的障碍物均为规则图形。如果要将该算法应用于三维复杂场景，需要对场景中的障碍物进行极大似然的近似，将其近似为圆、矩形或正方形等规则图形，这样做不仅工作量巨大，而且会丢失很多周围的环境信息，因此该算法不适用于高维状态空间。

目前面向该场景的相关工作较少，暂时未找到可参考的案例。故此本文所提出的基于深度强化学习算法的路径规划算法虽然需要额外训练，但其具有更好的适应性、灵活性和应对高维状态的能力，以及具有能够自主地学习和优化路径规划策略［10-11］的优点，可使其成为解决城市战场突防任务的有力工具。

1 问题描述

当涉及军事行动时，突防行动的路径规划是一项具有挑战性的任务。针对真实的城市战场，需要考虑多种因素，这些因素包括但不限于道路网络、建筑物位置和形状、障碍物位置和形状、交通流量、天气、时间等。对于道路网络，可以从卫星图像或其他地图数据中提取信息以构建拓扑结构，帮助完成任务的整体规划。但对于城市街道场景这类具体场景，智能装备需要面对敌方干扰和许多具体的障碍物如垃圾桶、小车、路障等，这些障碍物形状特征差异较大，难以用规则的几何形状表示。同时真实的智能装备需要通过自身的各类传感器获取周边信息，辅助做出行为决策。因此为了更好地将深度强化学习算法应用于城市战场突防任务，动态地实现路径规划，需要对城市战场环境和智能车建模，以更好地描述任务、设计算法流程和实验方案。

本文搭建了基于机器人操作系统（Robot Operating System，ROS）的智能车模型，用于深度强化学习算法的训练。本文所构建的智能车搭载了激光雷达传感器用于感知周围环境，整体架构如图2 所示。传感器的各项参数配置将在实验部分介绍。

图2 智能车整体架构

在突防任务当中，智能车需要时刻获取周围场景信息，例如自身当前的位置、目的地与车头所在方向的夹角、周边障碍距自身的信息。本文主要通过车载激光雷达获取周围场景的信息，具体模型如图3所示。

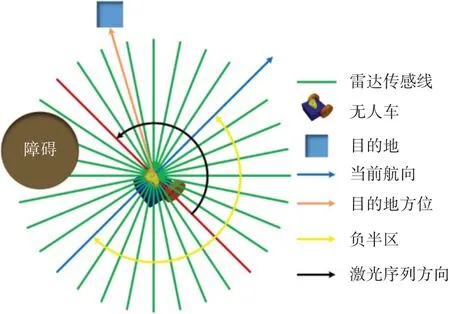
图3 智能车环境感知模型

如图3 所示蓝色箭头方向为车辆的前进方向，黄色箭头线覆盖区域为车辆负半区，与之对应的为后半区域，橙色箭头线指向目的地，激光雷达传感器所获取的环境信息S=［l1，l2，…，l180］（绿色线条），序号沿着黑色箭头方向递增。

每条激光雷达射线获取信息的处理公式如式（1）所示，其中si为激光雷达第i条射线探测到与障碍物之间的距离。

设（xg，yg）和（xs，ys）分别是目的地和智能车的绝对坐标，其中目的地与车辆之间的位置关系（ρ，θ）计算公式如下：

2 深度强化学习算法简介

2.1 马尔可夫决策

“试错”是强化学习的核心思想，而马尔可夫决策过程（Markov Decision Process，MDP）作为强化学习的理论基础，是一种无记忆的随机过程。MDP 基于智能体与环境之间的交互，以表示智能体在环境中的随机决策与回报，其模型要素可表示为（S，A，P，R，γ），其中：

S是状态集合，用于描述整个MDP 所有可能存在的环境状态。

A是动作集合，用于表示智能体在整个MDP 所有可能做出的决策结果。

P表示决策条件，表示智能体在t时刻st状态下采取动作a后，在t+1时刻的状态st+1的状态为s'的概率，其状态转移关系式如下：

R是评价函数，表示智能体在状态s执行动作a后状态转移到s'对任务目标的量化评价，其定义如下：

γ是折扣因子，表示MDP 中每次决策对未来决策的影响程度，当γ≤1时说明算法本身更加关注当前奖励。

MDP 的整体流程如图4 所示，智能体在状态st下做出动作at并根据状态转移策略转移到状态st+1，同时算法对智能体给予奖励rt（st，at，st+1），并不断循环执行该过程，直到达成最终任务目标［12］。

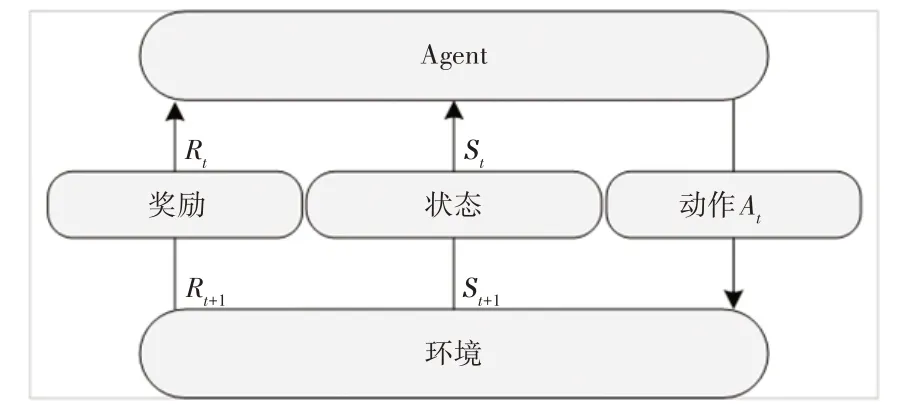
图4 马尔可夫决策过程

2.2 深度强化学习

深度强化学习作为解决复杂系统的感知决策问题的有效方法，通过结合深度学习的感知能力与强化学习的决策能力，实现了端到端的感知决策过程。深度Q 网 络（Deep Q-Network，DQN）［13-14］通过融合Q-Learning 和神经网络，使得其在一些游戏中能够做出比人更优的决策。此后在此基础上不断改进创新，提出了多种深度强化学习算法，目前主流的算法包括：深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）［15-16］、优 势 动 作 评 价 算 法（Advantage Actor-Critic，A2A）［17］、信赖领域策略梯度优化（Trust Region Policy Optimization，TRPO）［18］、近似策略梯度优化（Proximal Policy Optimization，PPO）［19-20］等，在游戏、自动驾驶、工业设计等诸多领域均取得了许多成果，表明了深度强化学习在高维环境状态和动作决策问题上具有优越性。

D3QN（Dueling Double Deep Q-Network）算法［21-23］是在DQN 算法的基础上进行改进的一种算法，主要的改进包括模型结构和训练方式。模型结构的改进使用了Double DQN［24］，通过使用一个网络（评估网络，Evaluaton Network）选择最佳动作，通过另一个网络（目标网络，Target Network）来估计Q值。这样可以减少Q值的偏移估计，从而提高学习效率。训练方式的改进是D3QN 在多台机器上同时运行多个代理程序，每个代理都是一个独立的DQN 学习算法的实例，提高了算法的训练效率。

本文面向三维城市街道场景，设计离散的动作空间简化问题的求解过程，因此D3QN 算法十分契合解决本文所遇到的问题。

3 面向城市战场的智能车自主导航深度强化学习算法

在城市战场突防任务中，由于智能车的动作是连续的，这使得强化学习的训练难度增加。同时，评价策略又需要实时根据任务进度改变比重，而传统的奖励函数无法随任务进度变化，难以满足要求。因此，为了解决上述问题，需设计出合适的深度强化学习算法。本文设计面向智能车的离散动作空间，并提出基于任务完成度的奖励函数，设计算法框架和流程，以更好地完成算法的学习和训练。

3.1 离散动作空间设计

在实际任务中，智能车的动作需要连续执行，这使得深度强化学习的动作空间变得非常大，从而增加了自主导航任务的求解难度［25-26］。因此，本文设计离散的动作空间来简化智能车的控制参数，以加快算法的训练速度。例如可以将车辆的移动简化为左转、右转、直行和停止等离散动作，通过这些动作的组合可以获得有限的动作空间。表1 为本文设计的动作空间，其中1 m/s 表示车速，0 m/s 表示静止；0 rad/s表示保持当前朝向，-1 rad/s 表示以1 rad/s 的角速度逆时针转向，反之表示顺时针转向。

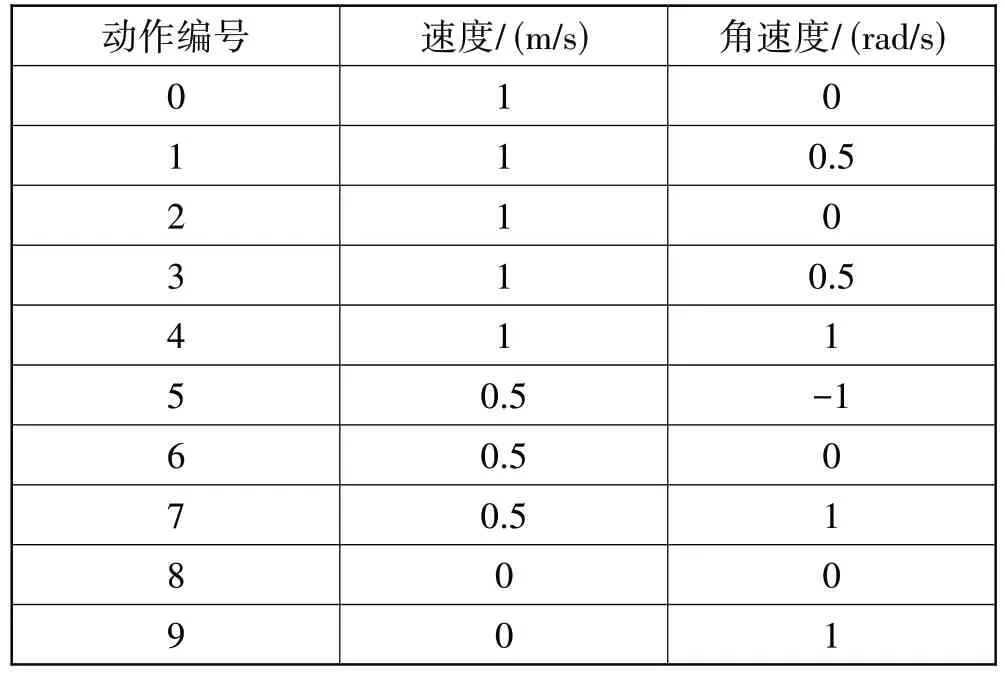
表1 离散动作设计

采用离散动作空间不仅可以简化模型的训练过程，还可以加快模型的训练速度。同时，相对于连续的动作序列，在自主导航任务中使用离散动作空间也可以获得更好的控制效果。

3.2 基于任务完成度的奖励函数设计

虽然深度强化学习在解决决策类问题方面表现出色，但奖励函数的设计对于算法的训练和模型的表现至关重要，传统的线性奖励函数无法根据任务进度提供合适的奖励。因此本文针对城市战场突防任务设计基于任务完成度的奖励函数，以实现不同任务进度下的奖励计算［27］。

如图5 所示，当β＞1 时奖励系数可随着任务进度的增加不断增大；当β=1 时，奖励系数恒为1，与传统奖励函数相同；当β＜1时奖励系数可随任务进度不断减小。本文称其为奖励基数（Reward Base，RB），记为β，其计算公式如式（5）。其中r为总奖励，d为任务完成度，ri与βi分别为对应的传统奖励和奖励基数。

图5 基于任务完成度的奖励系数变化曲线

在城市战场突防任务中，为了避免智能车在距离目的地较远的情况下频繁改变动作，定义了智能车动作变化量和任务完成度的计算公式如式（6）所示。其中v、w表示智能车的速度与角速度，ρ表示智能车与目标之间距离。

基于式（5），选取β=1.5，奖励函数计算公式如下：

综上所诉，通过调节RB 的大小可以计算出合适的连续任务进度下的奖励系数，制定出更合理的奖惩策略，有利于强化学习模型的训练。

3.3 算法框架和流程

通过结合Gazebo 仿真平台和ROS 以及D3QN 算法，本文设计面向城市战场的智能车自主导航算法框架和流程，整体架构如图6所示。

图6 智能车自主导航算法流程

具体步骤如下：

步骤1构建2个具有一样深度宽度和初始参数的神经网络分别来表示预测网络θ和目标网络θ'，并初始化算法参数和经验缓存池。

步骤2初始化训练环境并返回状态向量st。

步骤3通过预测网络计算st的Q值，并根据εgreedy策略从智能车的动作空间选择动作。

步骤4执行选择动作，并产生新状态st+1，奖励r和回合结束标记done，其中奖励r依据公式（7）计算。

步骤5将［st，at，rt，st+1，done］添加到经验缓存池中。

步骤6若done 为真，则回合结束依据退火算法更新探索率ε，依据公式（8）更新，返回步骤2，否则继续。

步骤7从经验缓存池当中随机选取n个样本［st，at，rt，st+1，done］k，k=1，2，3，4，…，n，用于预测网络θ的训练。

步骤8当达到目标网络更新频率，则利用预测网络θ更新目标网络θ'。

步骤9更新状态st=st+1，返回步骤3。

步骤10重复步骤3~步骤9 直到达到一定的训练步数或者达到预设的奖励。

4 仿真实验设计及结果分析

为了验证算法在突防任务中的有效性，本文在Ubuntu20.04 上使用ROS 和Gazebo 构建一个智能小车和虚拟仿真环境。本文分析模型的平均奖励、探索率变化、探索步数和Loss 值与训练轮数之间的关系，并通过可视化仿真环境验证最终模型的有效性和稳定性。

4.1 实验场景描述

在不影响问题求解的情况下，本文在Gazebo 仿真环境中搭建一个简化的城市街道场景，场景大小为20 m×20 m，该场景中设置了多种障碍物，由沥青路面、护栏、锥形桶、木头车和地锁等代替城市内各种物体，作为智能车路自主导航的训练场景，如图7所示。

图7 实验场景

智能车的初始位置位于场景中心，其初始坐标为（0，0），目的地坐标则随机选取10 个预设坐标中的1个，10 个预设坐标为（-5.2，3.3），（-7.0，1.44），（-6.0，2.2），（-5.8，-3.0），（3.0，5.6），（2.2，-6.0），（9，-6.8），（-2，5.9），（-6.0，4.0），（6.6，2.5）。

表2列出了本文实验所搭建激光雷达的各项参数。

实验搭建了基于ROS 的智能车控制系统，用于为智能车提供基于深度强化学习算法的导航避障训练。智能车与ROS主题之间的数据交换流程如图8所示。

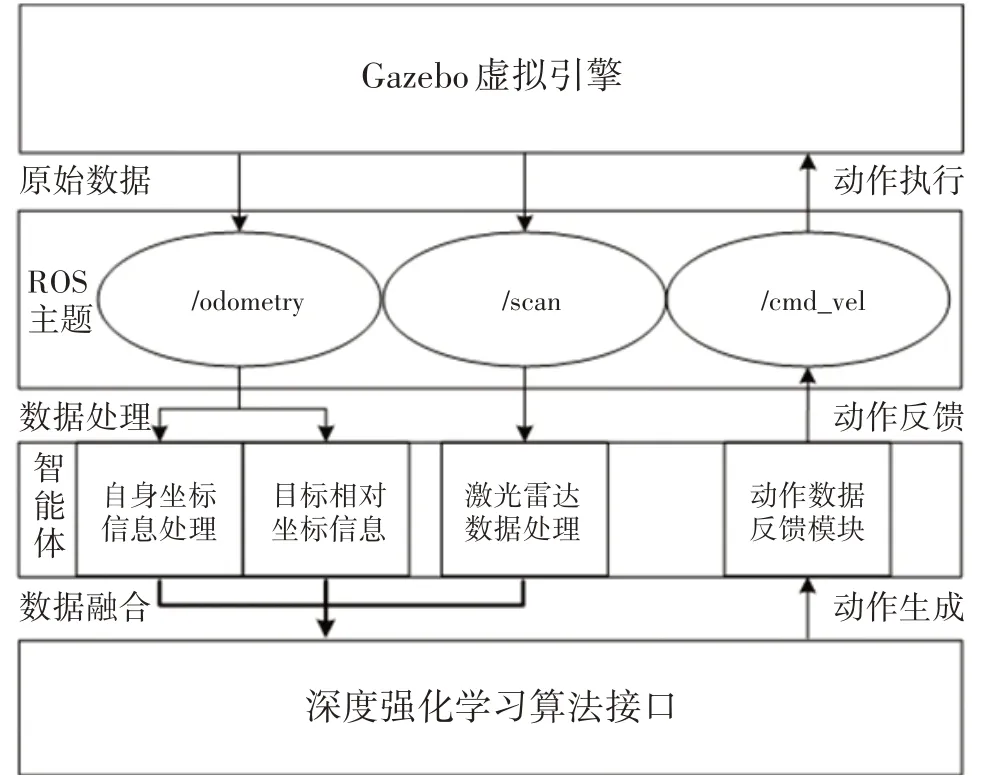
图8 智能车控制架构模型

4.2 参数设置

表3 为神经网络参数设置。本文实验中，状态空间大小由激光雷达数据和智能车、目的地之间的位置关系和任务结束符共同决定，即［S，ρ，θ，done］大小为183；动作空间大小为本文设计的离散动作的数量；由于实验设计的离散动作只有10 个，因此选用宽度为256的3层神经网络足以表达状态与动作之间的映射关系；BatchSize 大小参考网络宽度大小设置，选择0.001的学习率既可以保证模型在训练过程中不会过早拟合，又能避免训练时间过长影响实验结果产出。

表3 神经网络参数设置

表4 为算法相关参数设置。实验数据表明智能车单个回合的平均步数为在300 步，所以设置每回合最大步数为1000 步既可以保证实验前期模型的探索能力，又可以测试实验后期模型是否具有连续导航的能力；经验池的大小越大越好，本文实验中106条经验可以大约包含500 回合以内的数据；采样数量与BatchSize大小保持一致，折扣因子选取0.99加大模型对于长期收益的期望；0.99450≈0.01，因此0.99 的退火系数和0.01的ε-greedy策略终止参数可以赋予模型约450回合的探索时间，充分保证模型前期的探索能力。

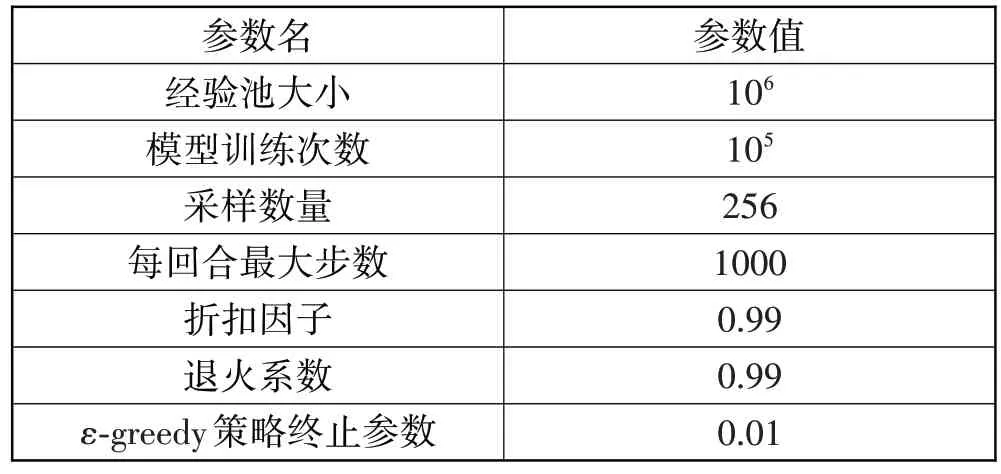
表4 算法参数设置

4.3 奖励函数设置

表5 为本文实验的奖励函数设置，其中d表示初始时智能车与目的地之间距离，dt表示当前距离，dt-1表示前一刻距离；vt表示当前速度，vt-1为上一次速度；wt表示当前角速度，wt-1为上一次角速度。

4.4 实验结果分析

4.4.1 奖励函数与ε退火策略曲线

奖励曲线可以直观地反映出模型的训练效果，ε-greedy 策略变化曲线可以展示模型训练过程中的探索能力的变化。图9 和图10 分别为每100 轮平均奖励变换曲线图和ε变化曲线图。

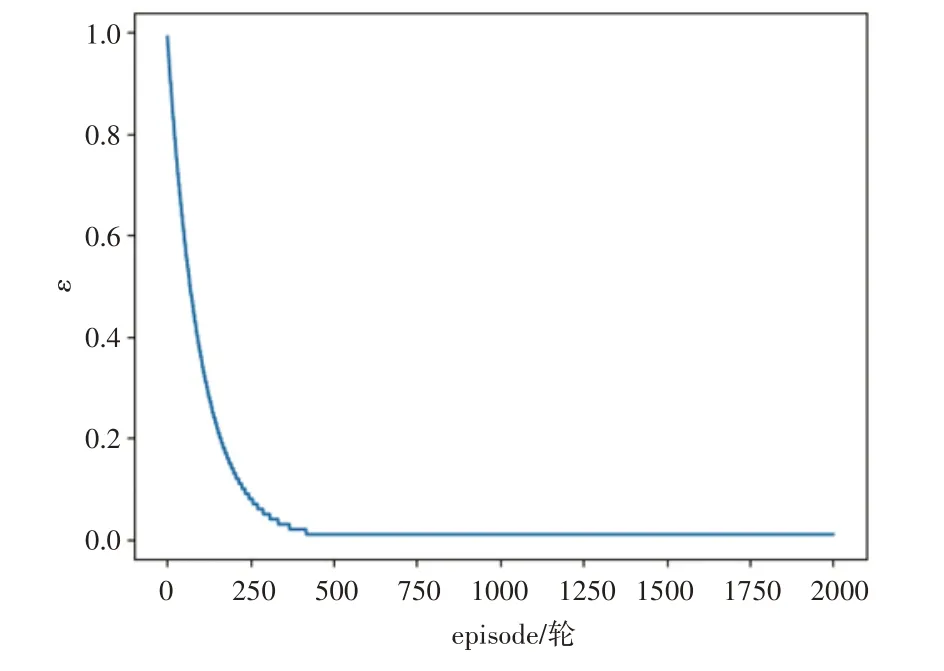
图10 ε变化曲线图

从图9 和图10 可以观察到，算法在训练过程中，平均奖励在约2000 轮时开始显著提升，在5000 到7000轮之间变化缓慢，在7000轮之后逐步提升，由于环境限制，本文实验只迭代了104轮。ε-greedy 策略初始值为1，采用退火算法衰减，其中衰减系数为0.99。在200 轮之前贪婪系数ε快速衰减，算法的探索能力逐步开发能力增强，约在400 轮时ε达到最小值，此时算法的开发能力最强，探索能力最弱。

4.4.2 损失函数与平均步数分析

损失函是评价算法收敛程度的重要参考依据，图11 展示了训练过程的损失函数曲线。为了方便展示，仅展示了5000 轮训练的损失函数变化曲线。从图11 中可以看出，约在1000 轮时损失达到最大值，2000 轮之后损失变化幅度较小，总体来看，该算法模型能够快速收敛。

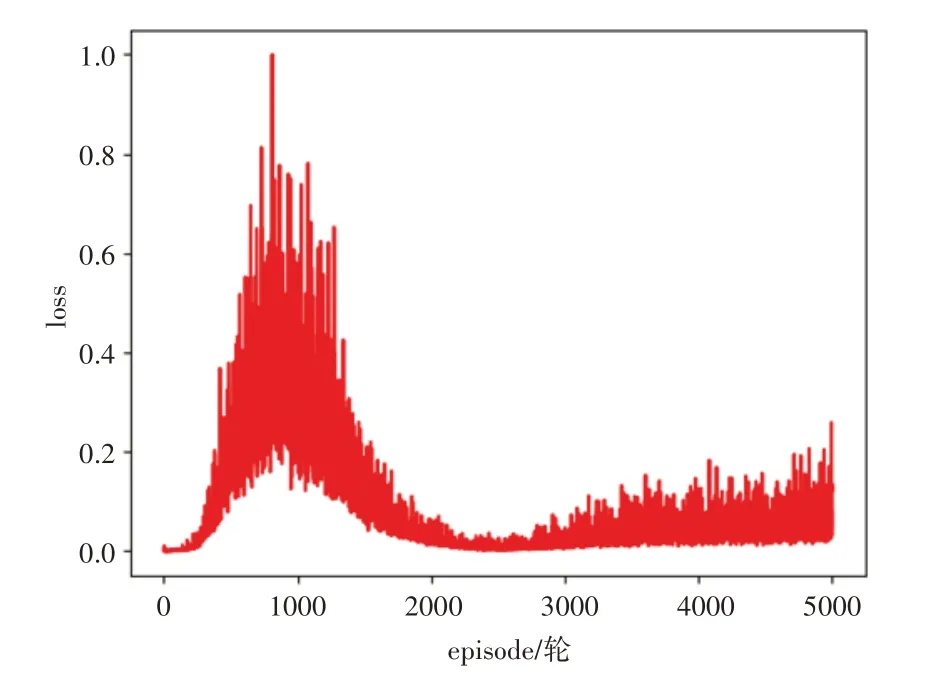
图11 损失值变化曲线

由于本文实验训练过程中，采用的是碰撞结束任务的策略，即当智能车到达目的地后，选择变化目的地继续当前回合，发生碰撞终止任务。因此，智能车到达的目的地越多，单个回合执行的步数也往往越多。图12 展示了训练过程中每100 回合的平均执行步数。从图中可以看出，模型在训练过程中单个回合的执行步数越来越多，这也侧面说明了模型能够较好地连续完成导航避障任务。

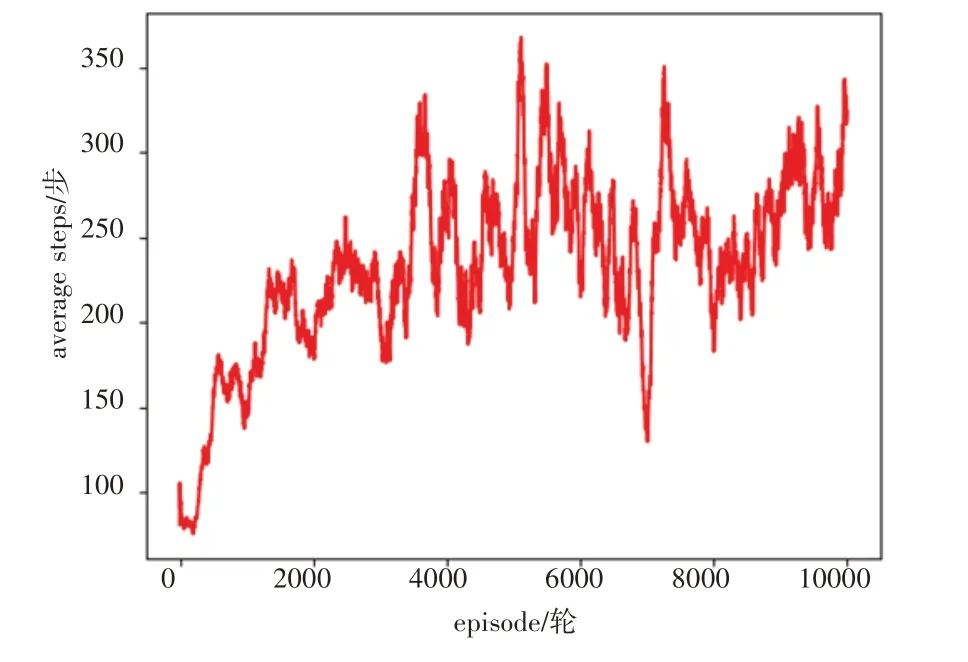
图12 单回合平均探索步数

4.4.3 运行结果和时间代价分析

实际运行结果和时间代价是最终展示模型有效性的标准。图13 展示了从初始位置出发连续变化5次目的地时智能车的运行轨迹。表6 展示了从初始位置到各预设目的地的执行时间和回合步数。

表6 到达各目的地的执行时间和回合步数

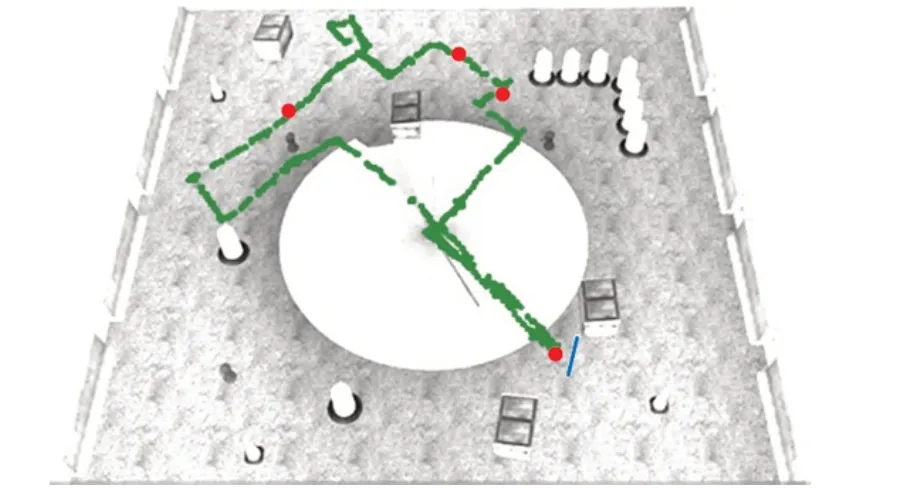
图13 运行结果展示

图13 中展示的路径为智能车连续以（6.6，2.5）、（-6.0，2.2）、（-7.0，1.44 ）、（-5.8，-3.0）、（6.6，2.5）为目的地所形成的路径，图中蓝色小圆柱为初始目的地标记，红色圆点为其他目的地标记。从实际运行结果分析，智能车的实际行走路径并非最优路径，且由于设计了基于任务完成度的奖励函数，使得智能车距离目的地较远时不会优先改变方向，但可以避免智能车前期频繁地发生速度和角速度的变换。同时，由于智能车依赖自身传感器数据获得动作，因此即使相同的目的地，其最终运行轨迹也可能不相同。然而，总体来看，通过该算法模型，智能车能够依靠自身的局部感知数据实现自主导航。

表6 展示了智能车从初始位置（0.0，0.0）分别到达各目的地的实际执行时间和回合步数。其中，平均执行时间为9.7 s、平均回合步数为184.3 步、单步响应时间约为0.05 s。这些数据表明，最终模型能够及时快速地响应完成既定任务。同时数据显示，距离越远实际执行时间和回合步数也越大。虽然二者之间存在相关性，但并没有严格的对应关系，这主要与场景环境和障碍物的具体位置有很大关系。因此表6所展示的数据，并不能完全代表模型每次的实际执行时间和回合步数。

5 结束语

本文面向城市战场提出了一种智能车自主导航方法，以解决传统算法在城市突防任务中遇到的问题，如依赖精确地图和无法应对高维状态空间等。该方法基于深度强化学习算法，设计了离散的动作空间和基于任务完成度的奖励函数。同时，本文还搭建了基于ROS 和Gazebo 的仿真训练环境，用于验证该方法的有效性。实验结果表明，该方法能够自主规划路径、快速收敛并保持稳定性，在连续变化目的地的情况下仍能取得不错的效果。然而，目前该方法仍然存在一些问题需要改进，例如使用离散的动作空间和单一的传感器数据训练强化学习模型与真实战场任务需求的差距，以及训练需要大量数据和计算资源、容易受到噪声和局部最优的影响等。因此，这些问题需要进一步改进，以提高该算法的实用性和效率。综合理论和实验，本文用深度强化学习算法构建智的能车自主导航模型，在街区战场突防任务中能够取得一定效果。