基于PWLCM和秃鹰俯冲机制改进的野狗优化算法

欧基发，蔡茂国，洪广杰，詹楷杰

（深圳大学电子与信息工程学院，广东 深圳 518060）

0 引 言

优化问题是社会各个领域逃避不了的一个问题，例如自动化［1］、计算机科学［2］、电力［3］、交通运输［4］等众多领域。然而使用梯度下降法等旧式数学方法已经难以解决当今社会大规模的优化问题。元启发式算法应运而生，其具备通俗易懂、易于实现等优点，逐渐成为人们解决优化问题的一种常规手段。元启发式算法通过对决策空间的部分子集进行采样来搜索优化解，成为解决黑箱优化问题的有效途径［5］。目前，除了蚁群算法［6］、遗传算法［7］和粒子群算法［8］等经典算法，麻雀搜索算法［9］、哈里斯鹰优化算法［10］、蝴蝶优化算法［11］和萤火虫优化算法［12］等算法也是人们使用得比较多的元启发式算法。在科技迅猛发展的时代里，旧的元启发式算法不断被改进优化，甚至被新的元启发式算法取代更替。

野狗优化算法（Dingo Optimization Algorithm，DOA）的工作原理简单明了，具有较强的全局开发探索能力，其寻优速度也有不俗表现［13］，已应用在网络带宽选择［14］、光伏组件参数提取［15］、特征选择［16］和粒子滤波器导航［17］等领域中。

元启发式算法普遍存在寻优速度偏慢、收敛精度偏低等现象，作为其子集的野狗优化算法也存在相同的情况。针对上述问题，学者从种群的初始化、野狗的群体攻击策略、迫害策略和种群生存标准等方面着手对DOA 进行一系列改进。Almazán-covarrubias 等人［18］利用局部搜索，对生存标准进行修改，来实现更佳的种群更替。Chaabane 等人［16］通过正弦切混沌映射策略初始化种群和引进惯性权重来改进群体攻击和迫害策略得到CDOA，并将该算法结合深度学习应用到光谱传感特征选择领域中。蔡新雷等人［19］将原来判断野狗种群行为的固定概率值P和Q修改成动态概率值，形成的IDOA 应用到电车调峰领域中，取得了良好的效果。然而这些改进的算法在寻优的速度和精度上仍有很大的提升空间，全局搜索以及收敛精度等有待深究。

上述研究表明野狗优化算法存在应用价值和研究意义，并为改进野狗优化算法提供了一些研究方向，因此本文提出一种基于PWLCM 和秃鹰俯冲机制改进的野狗优化算法。

1 野狗优化算法

野狗优化算法模拟了澳洲野狗在自然界生存时的行为，主要由4 个部分组成：群体攻击策略、迫害策略、食腐策略和种群更新。澳洲野狗种群补充生存发展的能量是通过狩猎活物（兔子、绵羊和爬行动物等）或者食用腐肉（动物的遗体）来进行的。本章描述DOA工作的基本步骤。

1.1 初始化种群

野狗个体随机分布在大自然中各个位置，并根据3种策略寻找食物补充能量。具体初始化公式如下：

1.2 群体攻击策略

当澳洲野狗种群在生存环境中发现大型活物时，它们便对该猎物进行包围、追逐，并发动群体攻击，共同分享食物。然而，包围体型巨大的猎物时，并非每个野狗都会对猎物进行攻击。澳洲野狗个体采用群体攻击策略时，其位置更新公式如下：

1.3 迫害策略

当野狗个体在觅食过程中发现个体比较小的猎物（例如兔子、老鼠等）时，野狗个体便会单独行动，并对小猎物进行追赶、迫害捕食。野狗个体在迫害小猎物过程中，其位置更新公式如下：

其中，β2是随机数，取值范围为［-2，2］；(t)是从野狗种群中随机选择出来的个体；r1为随机数，取值范围为1到最大野狗数，其中i≠r1。

1.4 食腐策略

野狗种群在寻找食物过程中如果没有发现活的猎物，就会将找到的动物遗体等腐肉作为食物来摄取营养维持种群的生存和发展。野狗个体在寻找腐肉充饥过程中，其位置的更新公式如下：

其中，σ是随机生成的二进制数，即σ∈ {0，1} 。

1.5 3种不同策略对应的条件

采用群体攻击策略、迫害策略和食腐策略等3 种狩猎策略是通过生成2个随机概率值（P1和P2）和2个预设概率值（P和Q）进行比较实现的。

第一个判断是判断野狗是否找到活的猎物，包括体型小的猎物和体型大的猎物：当第一个随机概率值P1＜P时，野狗找到活的猎物；否则，野狗找不到活的猎物，只能通过清除生存环境中的腐肉来维持生存。

第二个判断是判断当野狗找到活的猎物时，根据猎物的体型大小采取的是群体攻击策略还是迫害策略。即当P2＜P时，野狗种群觅食到体型较大的猎物时，采用群体攻击策略；否则，野狗个体觅食到体型较小的猎物时，采用迫害策略。总的判断依据如下：

1.6 种群更新

DOA 通过每只野狗的位置信息来确定其适应值，其中个体适应值越大对应的生存率越低。根据“适者生存”法则，当野狗个体生存率低于某个数值时，说明该个体不适应当前的生存环境，就会被大自然淘汰。基于野狗种群规模趋于稳定，其种群规模大小默认不会有变化，而那些被淘汰的野狗将会由新的个体替代。

1.6.1 适应值计算

野狗个体的适应值等于该只野狗各维度上对应的位置信息的平方和。

其中，fitness（i）是第i个野狗个体的适应值，positionk*（i）是第i个野狗第k个维度上的具体位置信息。

1.6.2 生存率计算

通过公式（7）对野狗个体的生存率在［0，1］区间内进行归一化。

其中，survival（i）是第i个野狗个体的生存率，fitnessmax是野狗种群中最大的适应值，其生存率最小，对应的生存率值为0；fitnessmin是野狗种群中最小的适应值，其生存率最大，对应的生存率值为1。

1.6.3 野狗个体更替

2 融合多种策略改进的野狗算法

2.1 基于PWLCM 的种群初始化

DOA 在初始化种群个体时划定边界，在指定的空间内得到的野狗个体种群分布不均、质量参差不齐，种群多样性得不到保证。使用质量欠佳的种群进行迭代不仅会让算法求解精度下降，而且也会降低算法寻优效率。而混沌映射在解决伪随机数序列存在的问题上表现不俗，能够让个体按照一定规则随机并均匀分布在特定的空间里。通过文献［20］可知，PWLCM 生成的随机序列拥有良好的遍历性、统计特性，能生成覆盖率高、质量高的种群。

见名识义，PWLCM（分段线性混沌映射）是将混沌值映射分成4 段，每一段都具备线性混沌的性质。利用PWLCM生成的种群，避免了极端的种群初始化问题的出现，不仅能加快原始DOA寻优速度，而且使得算法的求解精度得到一定程度的提升。通过文献［21］以及实验得知，当K=0.4时，PWLCM的性能较好。

2.2 融合秃鹰搜索算法的迫害策略

澳洲野狗在采用迫害策略捕食过程中，通过追踪猎物，直至猎物疲惫放弃挣扎。原始野狗优化算法在模拟这一过程时不经意间让自身的寻优速度偏慢，因此对这一策略进行优化改进能让野狗优化算法得到很大提升。而秃鹰搜索算法［22］具有极强的搜索能力，收敛速度快。通过引进秃鹰搜索算法中的俯冲捕获猎物机制能让野狗个体更快地靠近、捕获小猎物，即引进秃鹰俯冲机制能极大地改善野狗优化算法迫害策略的局部搜索能力差的问题。

其中，C1和C2为野狗迫害策略时的运动强度参数，取值范围均为［1，2］的随机数；A=10，为控制螺旋轨迹的参数；Pmean为野狗种群的平均位置。

2.3 基于改进的螺旋搜索因子的食腐策略

螺旋搜索因子分别被应用到飞蛾火焰优化算法（MFO）［23］和鲸鱼优化算法（WOA）［24］中。由文献［25］可知，改进的螺旋搜索因子能有效地增强算法在指定区域的探索和开发能力。本文在1.4节食腐策略中引进改进的螺旋搜索因子，以增强算法局部开发和寻找更优质解的能力。野狗个体位置更新公式如下：

其中，a∈(0，1)，是随机变量，U是控制对数螺旋曲线形状的定值参数，I是服从正态分布的随机变量。与原始的DOA 食腐策略相比，融合改进的螺旋搜索因子的食腐策略使得野狗个体呈螺旋状的方式进行寻优求解，让算法不会轻易地被局部最优所迷惑，从而使得算法的寻优精度在原基础上得到突破。

2.4 IDOA的伪代码

IDOA算法的伪代码如下：

输入：野狗种群数量SizePop。

1 初始化Iterations、Fn和Times等参数

2 PWLCM初始化野狗种群，计算个体适应值

3 参数设置：种群数量SizePop、P、Q

4 while Iteration＜Iterations do

5 if 随机数P1＜Pthen

6 if 随机数P2＜Qthen

7 使用式（2）更新群体攻击的野狗位置

8 else

9 使用式（18）更新迫害策略的野狗位置

10 end if

11 else

12 使用式（21）更新食腐策略下的野狗位置

13 end if

14 根据式（7）计算野狗个体的生存率

15 根据式（8）对低生存率个体进行种群更替

16 ifPnew＜P*then

17P*=Pnew

18 end if

19 Iteration=Iteration+1

20 end while

21 输出全局最优解

整个IDOA的算法流程图如图1所示。

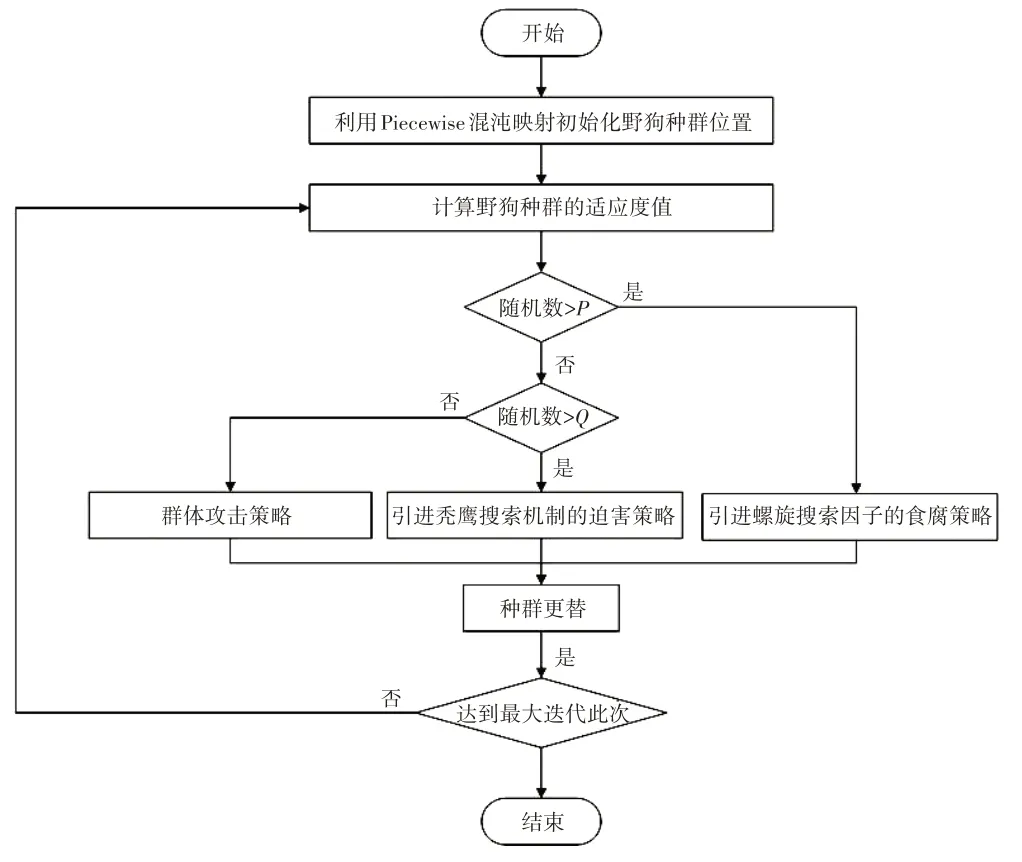
图1 IDOA流程图

3 算法的性能测试

3.1 测试函数

为了验证IDOA 的优良性能，选取8 个测试函数［26］进行仿真实验。这8 个测试函数的理论最优值均为0，其中F1~F5 是单峰函数，F6~F8 是多峰函数。仿真实验使用的函数信息如表1所示。

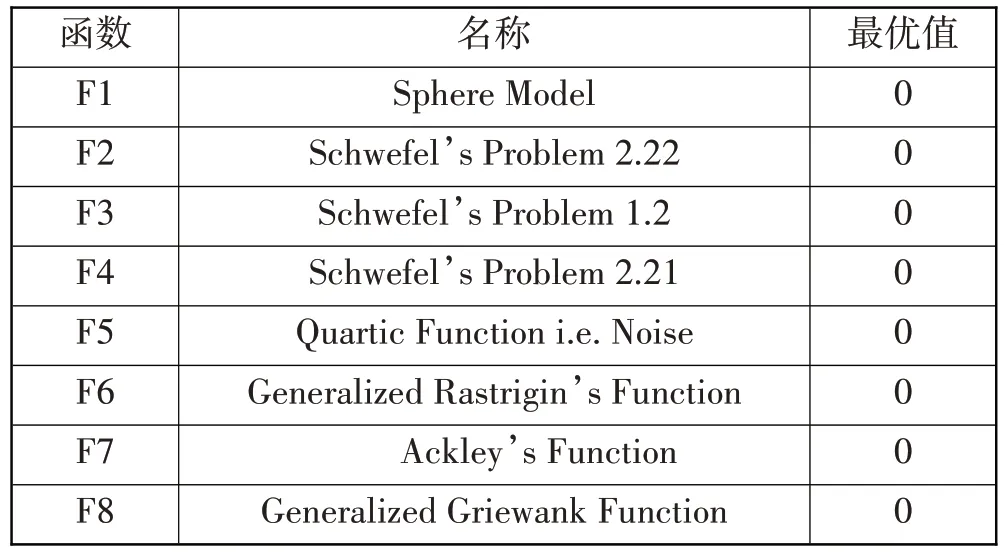
表1 测试函数

3.2 参数设置

参数设置如表2所示。

表2 参数设置

3.3 不同种类智能优化算法比较

为确保实验的公平有效，6 种算法的对比仿真实验均在同一环境下进行。即使用CPU 参数为11th Gen Intel（R）Core（TM）i7-11700、主频参数为2.5 GHz、内存大小为16 GB 的64 位Windows 10 操作系统的电脑设备上的R2021a版本的MATLAB 进行算法对比。将基于PWLCM和秃鹰俯冲机制改进的野狗优化算法（IDOA）同粒子群优化算法（PSO）［8］、灰狼优化算法（GWO）［27］、北方苍鹰优化算法（NGO）［28］、鹈鹕优化算法（POA）［29］、野狗优化算法（DOA）在8 个测试函数上进行实验对比。种群数量和迭代次数分别设置为30 和500 ，严格遵循8 种测试函数的维度、搜索上下界范围。通过仿真实验，可以得到6 种算法在8 种不同函数上的测试结果（见表3）：最优值、平均值以及标准差。其中表现最好的数据用粗体来表示。

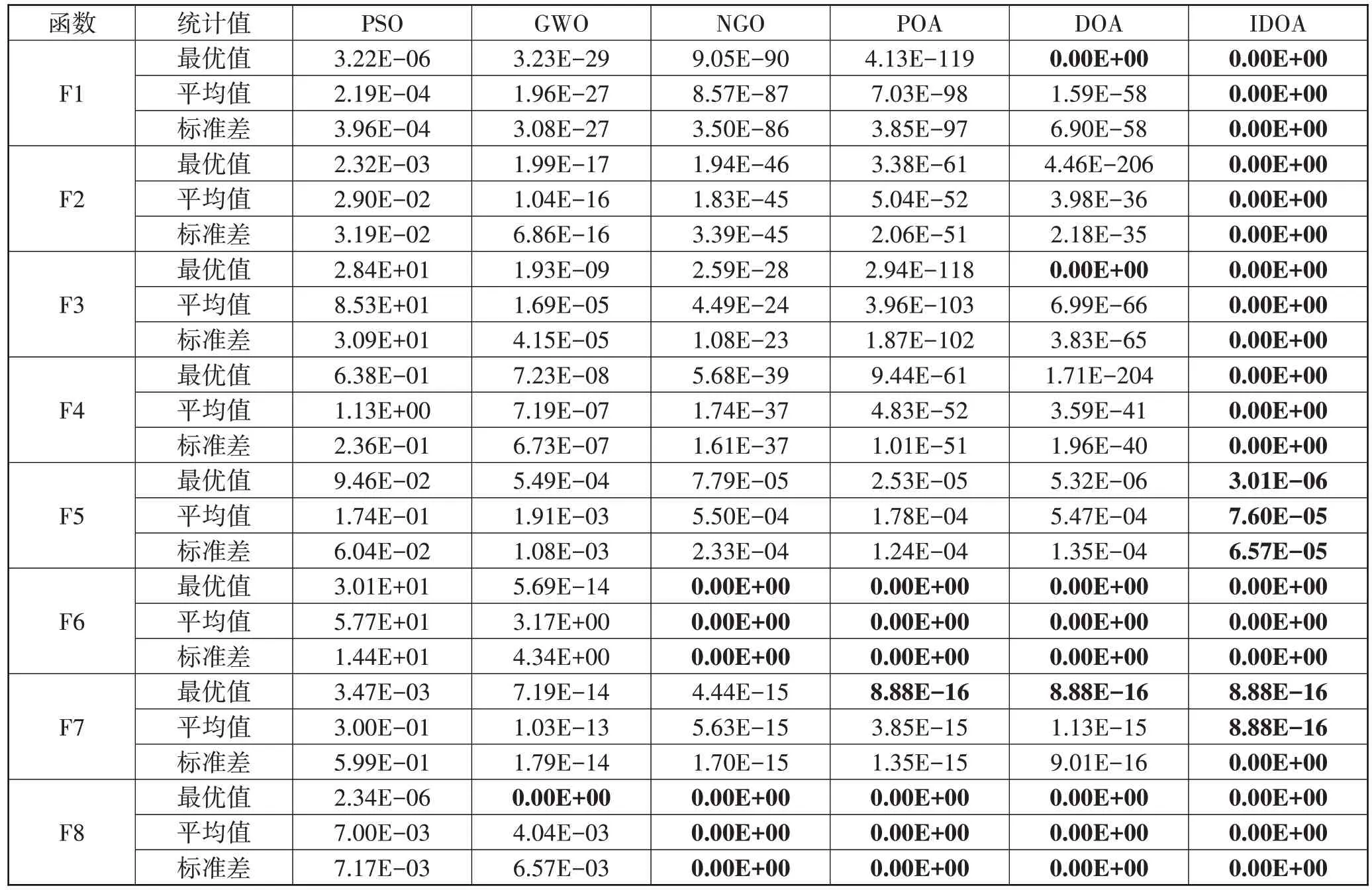
表3 IDOA与其它元启发式算法比较结果

3.4 IDOA与其它元启发式算法的比较

8种测试函数的收敛曲线图如图2所示。

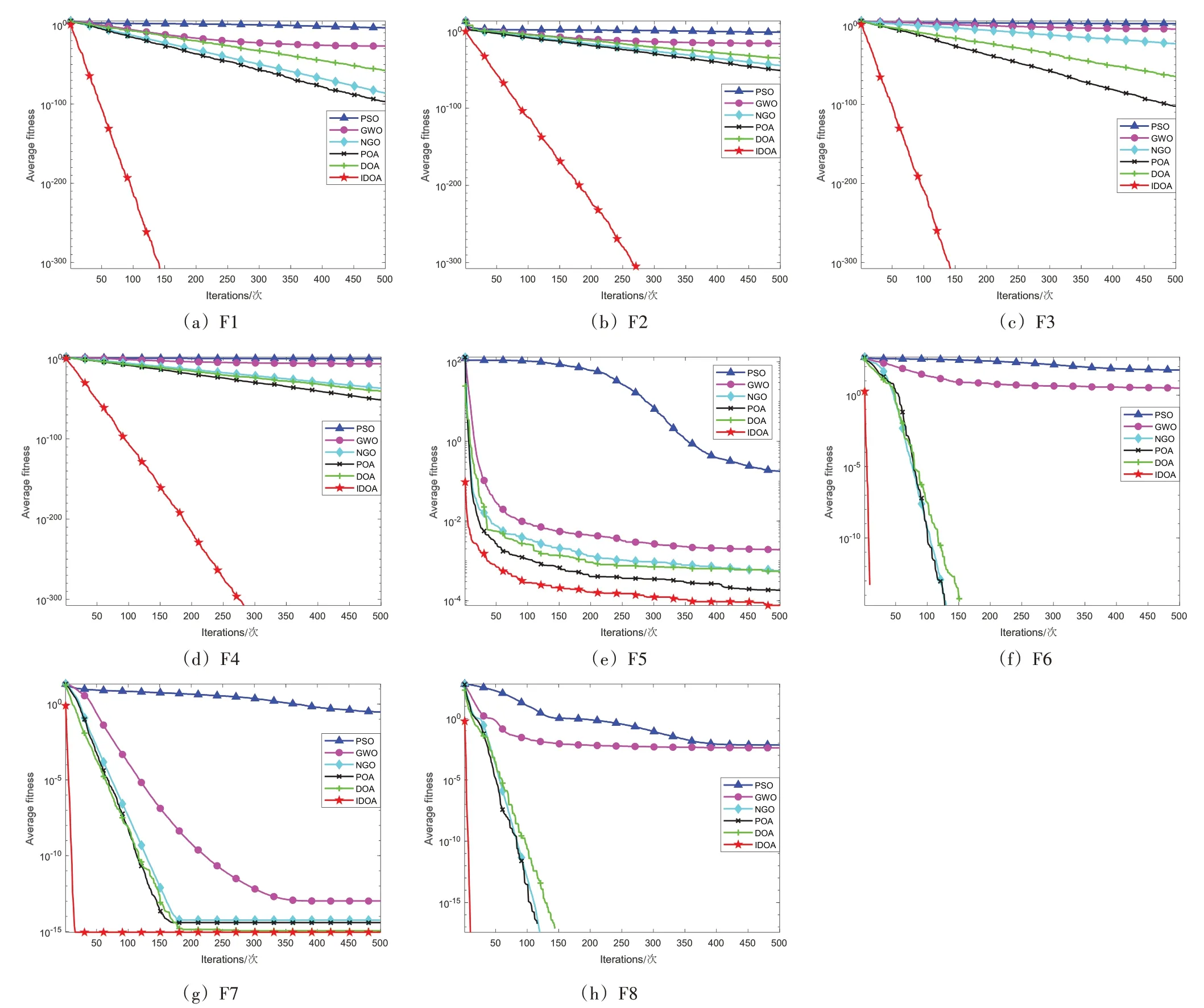
图2 8种函数的收敛曲线图

结合表3 和图2，从函数F1~F4 的收敛曲线图（图2（a）~图2（d））可直观地看到IDOA 的寻优速度和精度遥遥领先于PSO、GWO、NGO、POA、和DOA，并且只有IDOA 求解到最优解。对于函数F5 和F7（图2（e）和图2（g）），虽然所有算法均没有寻找到最优值，但是IDOA 的收敛速度和寻优精度明显优于其他算法。对于函数F6 和F8（图2（f）和图2（h）），与PSO 和GWO相比，IDOA 与NGO、POA、DOA的寻优精度表现更佳且它们之间平分秋色，但是IDOA 的收敛速度远快于其他算法，在迭代20次之前就收敛到最优值。

3.5 IDOA与其它改进的DOA的比较

为了验证 IDOA 与其他改进DOA 算法的优劣性，将本文的IDOA 与CDOA［16］、IDOA［19］进行对比分析。各算法的共有参数与3.2 节中保持一致，其他参数设置跟原文献保持一致，对比结果见表4，其中原文献中没有出现的数据用“-”表示。算法寻找到测试函数的最优值，表明该算法在该测试函数里达到最优，则记录该算法达到一次最优，该项数据则用粗体来表示。

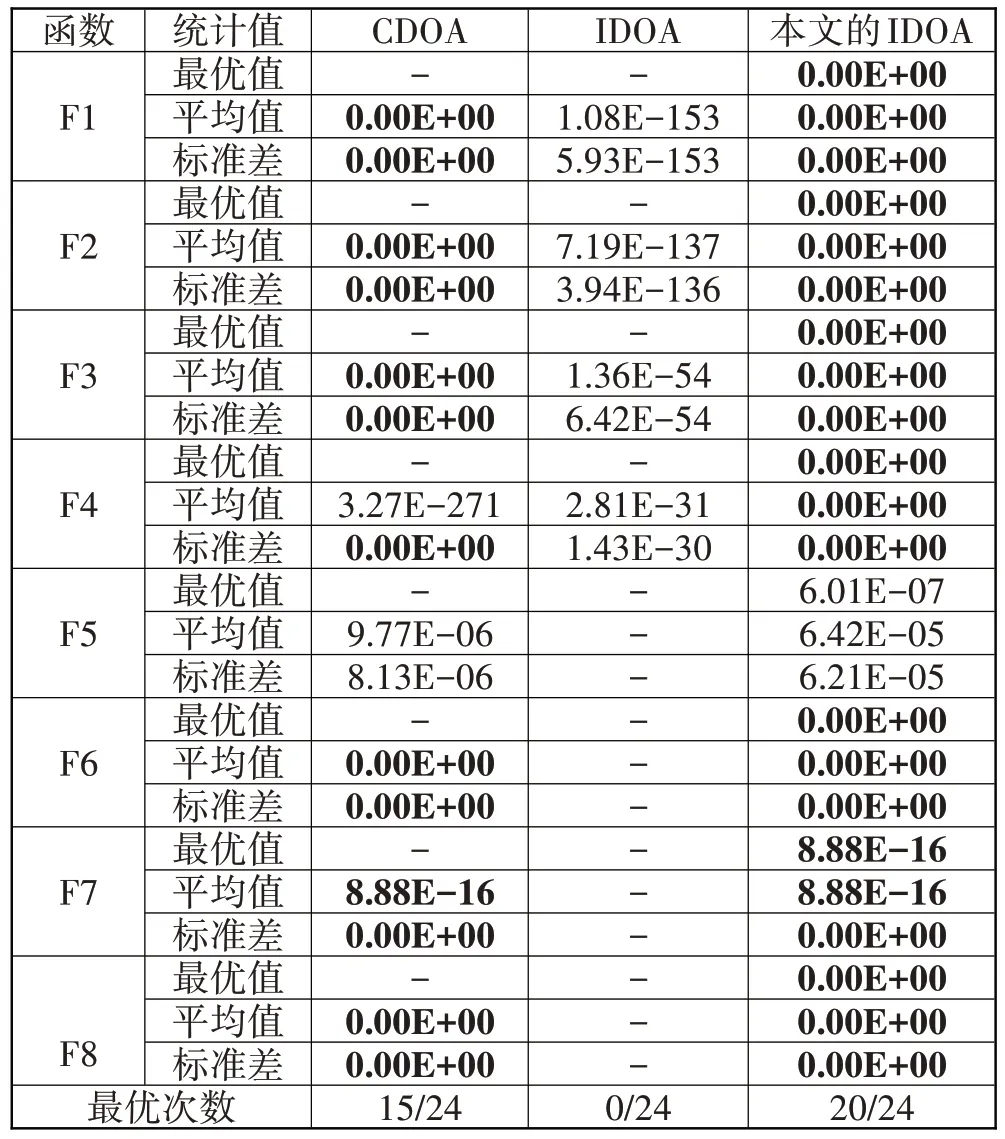
表4 IDOA与其他改进的DOA的比较分析

如表4 所示，对于函数F1~F3，本文的算法与CDOA 的寻优精度相同，与IDOA 相比，拥有巨大优势。对于函数F4，本文的IDOA 的平均值和标准差大幅度优于其他2种改进的算法。对于函数F5，因为本文的IDOA和CDOA这2种算法都是在DOA的基础上改进而来，故性能指标接近，但本文的IDOA 的寻优精度劣于CDOA。在函数F6~F8 中，本文的算法和CDOA 的平均值和标准差的表现不分上下。本文的IDOA 在8 种测准测试函数实验的24 项数据中，有20项占优；而CDOA 次之，有15 项占优；IDOA 表现最差，0 项占优。结果表明，兼顾精确度和稳定性，本文提出的IDOA的整体性能优于其他2种改进的DOA。

3.6 消融实验

为了验证IDOA 每一处改进的有效性，本文的IDOA 在3.1 节和3.3 节的实验环境下进行消融实验。其中DOA 利用2.1节的PWLCM 初始化种群改进得到IDOA1；DOA 利用2.1 节的PWLCM 初始化种群和基于秃鹰俯冲机制的迫害策略，改进得到IDOA2。各算法的共有参数与3.2 节中保持一致，其他参数设置跟原文献保持一致。即使用F1~F8 共8 个30 维的测试函数来进行仿真实验，进行30 次独立重复实验，每次独立实验中，算法迭代500次。对比结果见表5，其中较上一个算法在寻优精度上有提升，则用“↑”表示；无提升则用“→”表示；寻优精度有所下降则用“↓”表示。每项最优数据用粗体来表示。

表5 3个改进策略的消融实验

通过表5 可以看出，IDOA1 在F1~F5 和F7 这6 个测试函数上提升了DOA 的寻优精度，但算法的平均值仍未达到最优；在F6 和F8 中，IDOA1 的寻优精度和DOA 的保持一致。IDOA2 在F1~F4 这4 个测试函数上提升了IDOA1 的寻优精度；在F5~F8 中，IDOA2的寻优精度和IDOA1 的不分上下。IDOA 在F5 这1个测试函数上提升了IDOA2 的寻优精度；在剩下7个测试函数中，IDOA 的寻优精度和IDOA2 的旗鼓相当。

图3 中的算法收敛曲线图表明，在收敛速度方面，DOA＜IDOA1＜IDOA2＜IDOA，充分表明3处改进均提升了算法的收敛速度。综合表5 和图3，充分表明基于PWLCM 初始化种群、基于秃鹰俯冲机制的迫害策略和螺旋搜索因子的食腐策略都能提高算法的寻优精度和寻优速度。即充分表明了2.1 节、2.2 节和2.3节等3种改进方法的有效性。

图3 消融实验算法收敛曲线图

3.7 Wilcoxon秩和检验

为全面地评估IDOA 的性能，本节将使用Wilcoxon 秩和检验［30］进行统计分析，以此来验证IDOA和SSA、NGO、POA、BWO算法之间是否存在显著性差异。设定显著性水平为5%，并与Wilcoxon 秩和检验计算得到的P进行比较。当P≥0.05 时，表示比较的2种算法之间不存在显著性差异，实验结果中用“-”表示；当P＜0.05 时，则表示比较的2 种算法之间存在显著性差异，实验结果中用“+”表示；NaN 表示比较的2种算法性能旗鼓相当，不能进行显著性分析，实验结果统计中用“=”表示。

实验结果如表6 所示，可以看出大部分P值是远小于0.05 的。IDOA 跟PSO 和GWO 在8 个测试函数中存在显著性差异。此外，IDOA 跟NGO 和POA 在6个测试函数中存在显著性差异；在剩下的2 个测试函数里，不能进行显著性分析。而IDOA 跟DOA 在5 个测试函数中存在显著性差异；在1 个测试函数中不存在显著性差异；在剩下的2 个测试函数里，不能进行显著性分析。Wilcoxon 秩和检验的结果说明，IDOA的优化性能比其他5 种算法要好，具备更强大的寻优能力。

表6 Wilcoxon秩和检验结果

4 结束语

针对野狗算法寻优速度偏慢、求解精度偏低的问题，本文提出了一种基于PWLCM 和秃鹰俯冲机制改进的野狗优化算法。首先利用分段线性混沌映射初始化得到更均匀、高质量的种群；其次引进融合秃鹰搜索机制的迫害策略，有效地加速野狗个体捕获小猎物，即加快算法寻找最优解的过程；最后通过引入改进的螺旋搜索因子的食腐策略，增强了算法的局部探索开发能力，提高了算法寻优效率以及求解精度。而消融实验充分表明了3 种改进策略均能提高了野狗优化算法的收敛速度以及寻优精度。6 种算法在8个测试函数仿真实验结果以及Wilcoxon 秩和检验的结果都表明提出的IDOA 具有更快的寻优速度和更强的寻优能力。与最近改进的野狗优化算法相比，本文的IDOA 兼顾精确度和稳定性，呈现出更强的整体性能。