一类分数阶Laplace方程解的径向对称性研究

李升萍,周长亮

(东华理工大学理学院,330013,南昌)

0 引言

分数阶Laplace算子是一个非局部算子,其形式为

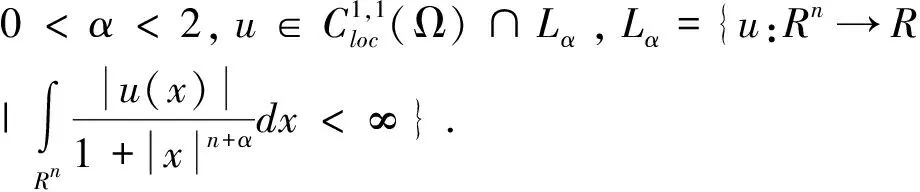
为解决非局部性这一难题, Caffarelli等[1]引入了延拓法。延拓法的核心在于将非局部问题转化为更高一维局部问题。对函数u:Rn→R,并将函数u在高一维的延拓记作U:Rn×[0,∞)→R,且U(x)满足

那么,u与U满足

这一方法得到了很好的应用[2-4]。

2006年, Chen等[5]通过证明微分方程与积分方程的等价性,引入了积分形式的移动平面法。证明了0<α<1时,微分方程

(1)

与积分方程

(2)

的等价性,对方程(2)通过积分形式的移动平面法得到正解u(x)的径向对称性。此后,积分形式的移动平面法得到广泛的应用[6-8]。

(3)

2021年,郭天培[15]利用移动平面法研究了以下Laplace方程

-Δu(x)=|x|βup(x)+|x|γuq(x),n≥3.

(4)

基于上述研究,本文主要采用直接移动平面法,将方程(4)的研究推广到分数阶上,考虑以下更为一般的分数阶Laplace方程正解的对称性。

(5)

1 准备工作

(6)

那么

Wλ(x)≥0,x∈Ω

(7)

同时,若存在x∈Ω使得u(x)=0,那么

u(x)=0,a.e.x∈Rn.

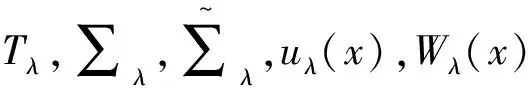
(8)

那么,对足够小的l,有

Wλ(x)≥0,x∈Ω.

(9)

同时,若存在x∈Ω使得u(x)=0,那么

u(x)=0,a.e.x∈Rn.

(10)

(11)

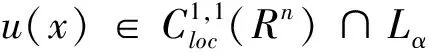
(12)

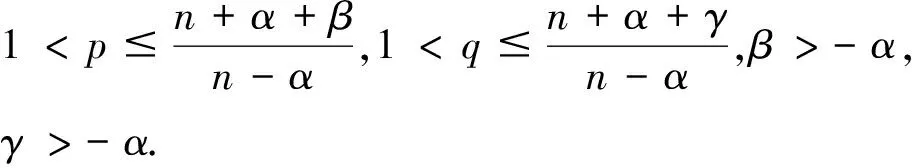
那么,存在常数C>0,使得对于任意小的ε和足够负的λ,有

Wλ(x)≥C>0,x∈Bε(0λ){0λ}.

证明:假设η(x)为一光滑截断函数,在Rn中η(x)∈[0,1],suppη(x)⊂B1且在B1/2内η(x)≡1。令

则有

由此可得,对任意足够大的|x|,存在常数C1>0,使得

(13)

对足够大的R>0,令

(14)

由式(13)、(14)、(17)可得

则由极大值原理可得

g(x)≥0,x∈BR,

即

当R→∞时,有

v(x)≥φ(x),x∈Rn.

(15)

利用式(15),当x∈Bε(0λ){0λ},即xλ∈Bε(0){0}时,有

vλ(x)≥φ(xλ)

对足够小的ε>0,存在C>0使得

vλ(x)≥φλ(x)≥2C>0.

当λ足够负时,根据v(x)在无穷远处的衰减情况可得

v(x)≤C,x∈∑λ.

因此

Wλ(x)≥C>0,x∈Bε(0λ){0λ}.

2 主要结论与证明

本节将采用直接移动平面法对方程(5)正解的径向对称性进行研究,主要证明以下定理。

2.1 主要结论

2.2 主要结论的证明

由于没有u(x)在无穷远处的退化条件,无法对u(x)直接使用移动平面法。为了克服这一困难,需对u(x)进行Kelvin变换。

令

(16)

是u(x)的Kelvin变换。经计算可得

(17)

其中,

τ1=n+α+β-p(n-α),τ2=n+α+γ-q(n-α).

任意选取x1的方向。对于λ<0,令Tλ={x∈Rn|x1=λ}为所需移动的平面,xλ=(2λ-x1,x2,…,xn)为点x关于平面Tλ的对称点,同时

vλ(x)=v(xλ),Wλ(x)=vλ(x)-v(x).

由中值定理可得

(18)

(19)

2.2.1 次临界条件

此时,τ1>0,τ2>0。

证明过程分为2步。

第1步, 证明对足够负的λ,有

Wλ(x)≥0,x∈∑λ{0λ}.

(20)

这可由引理3来实现。

首先,根据Wλ(x)的定义,有

(21)

因此,若Wλ(x)在区域∑λ内某点小于0,那么Wλ(x)的负极小值一定能在∑λ内取得。由引理4可知,对于足够负的λ,存在c0>0和ε>0,使得

Wλ(x)≥c0>0,x∈Bε(0λ){0λ}.

这说明Wλ(x)的负极小值不会在0λ上取得。

(22)

现在,对于λ≤-R0,必有Wλ(x)≥0,x∈∑λ{0λ}.

这验证了式(20)。至此完成了第1步的证明,并得到了移动平面Tλ的起始位置。

第2步,在保持式(20)成立的前提下,一直将平面Tλ从左向右移动,直至移动到其极限位置Tλ0,

λ0=sup{λ|Wμ(x)≥0,∀x∈∑μ{0μ},μ≤λ}.

接下来需证明

λ0=0,Wλ0(x)≡0,x∈∑λ{0λ}.

结合引理2与引理3即可证得。

由反证法可知,若λ0<0,将证明Tλ还可以向右再移动一小段距离,即存在ε>0,使得对任意的λ∈(λ0,λ0+ε)有

Wλ(x)≥0,x∈∑λ{0λ}.

(23)

这将与λ0的定义相矛盾。因此必有λ0=0。

现在结合引理2与引理3证明式(23)。由式(21)可知,Wλ(x)的负极小值不可能在BR0(0)外取得,接下来证明Wλ(x)的负极小值也不可能在BR0(0)内取得。

事实上,可以证明对于足够接近λ0的λ,

Wλ(x)≥0,∀x∈(∑λ∩BR0(0)){0λ}.

(24)

要想证明式(24),只需证明存在足够小的ε,δ>0,使得对任意的λ∈(λ0,λ0+ε),有

Wλ(x)≥0,∀x∈∑λ0-δ{0λ}.

(25)

若式(25)成立,则

Wλ(x)≥0,∀x∈(∑λ∑λ0-δ){0λ}.

(26)

首先证明式(25)成立。只需证明

Wλ0(x)≥0,∀x∈(∑λ0∩BR0(0)){0λ}.

(27)

当λ0<0时,必有

Wλ0(x)>0,∀x∈∑λ0-δ{0λ0}.

(28)

(29)

这与式(29)矛盾,因此式(28)成立。

由式(28)可知,存在常数c0>0和δ,使得

(30)

再由Wλ(x)关于λ连续可得,存在ε>0和ε<δ,使得对所有的λ∈(λ0,λ0+ε)

(31)

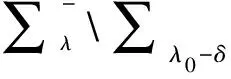
Wλ(x)≥0,x∈(∑λ∑λ0-δ){0λ}.

(32)

结合式(22)、(31)、(32)可得,对所有的λ∈(λ0,λ0+ε),

Wλ(x)≥0,x∈∑λ{0λ}.

(33)

这与λ0的定义相矛盾。因此,必有λ0=0。

同理,将平面Tλ从+∞往左移动可得

Wλ0(x)≤0,x∈∑λ0{0λ0}.

到目前为止,已经证得

λ0=0,Wλ0(x)≡0,x∈∑λ0{0λ0}.

即v(x)关于平面T0对称。由于x1的方向可以任意选择,实际上就已经证明了v(x)是关于原点径向对称的,因此u(x)也是关于原点径向对称的。

此时τ1>0,τ2=0。

(34)

(35)

此时τ1=0,τ2>0。

(36)

(37)

现对情形(2)、(3)综合分析。

由式(35)、(37)可得

均满足引理3的要求(10)。

接下来的证明过程与情况1)的证明过程相似。

第1步,证明对足够负的λ,有Wλ(x)≥0,x∈∑λ{0λ}。

第2步,保持Wλ(x)≥0,x∈∑λ{0λ}成立的前提下,一直将平面Tλ从左向右移动,直至移动到其极限位置Tλ0,

λ0=sup{λ|Wμ(x)≥0,∀x∈∑μ{0μ},μ≤λ}.

然后,结合引理2与引理3可证得

λ0=0,Wλ0(x)≡0,x∈∑λ0{0λ0}.

即v(x)是关于平面T0对称的。由于x1的方向可以任意选择,实际上已经证明了v(x)关于原点径向对称,因此,u(x)也是关于原点径向对称的。

这样就得到在情形(2)、(3)中,u(x)均是关于原点径向对称的。

此时τ1=0,τ2=0。

C(x)=pvp-1(x)-qvq-1(x).

第1步 ,与次临界条件下完全相同,利用引理3可得,当λ足够负时,

Wλ(x)≥0,x∈∑λ.

第2步,令

λ0=sup{λ≤0|Wμ(x)≥0,∀x∈∑μ,μ≤λ}.

情况1：λ0<0.类似于次临界条件下,结合引理2及引理3可证得

Wλ0(x)≡0,x∈∑λ0.

由此可知,0不是v(x)的奇点。因此,当|x|足够大时u(x)～|x|α-n,但由于β,γ>-α,在对u(x)直接运用移动平面法时,无法满足条件(10),所以只能通过证明v(x)关于Rn中某点径向对称来得到u(x)也是关于Rn中某点径向对称。

情况2：λ0=0.然后再将平面Tλ从+∞向左移动,可得Wλ0(x)≡0,x∈∑λ0,即v(x)是关于原点对称,故u(x)也是关于原点对称的。

在这2种情况下,u(x)都是关于Rn中某点径向对称的,故临界条件下方程(5)的正解是关于Rn中某点径向对称。这样就得到了定理1。

综上,利用移动平面法可得方程(5)在次临界条件下是关于原点径向对称的,而在临界条件下是关于Rn中的某点径向对称的。