民机雷达罩的抗鸟撞非线性力学行为仿真研究

庞小强,朱小龙,荆雲杰,龙舒畅,唐 维,王 焰,刘 卫

(1.中航成飞民用飞机有限责任公司,四川 成都 610092;2.华南理工大学 土木与交通学院,广东 广州 510641)

近年来,航空业取得了长足的发展,空难也引起了公众的关注。鸟撞问题是飞机在低空飞行阶段的一个主要问题,鸟类的撞击可以摧毁飞机结构[1]。统计数据显示,72%的坠机事故发生在150 m以下,92%的事故发生在900 m以下,即飞机的起飞和着陆阶段,而这类事故大部分都是由鸟撞引起的,因此,对飞机结构抗鸟撞问题的研究具有重大意义,这对飞机的飞行安全至关重要[2]。

复合材料由于重量轻、强度高,在飞机上有着广泛的应用。由于铺层复杂多样,复合材料结构具有显著的各向异性特点,在鸟撞、冰雹等作用下,其损伤模式相较于传统的金属、合金结构更加复杂。因此,研究复合材料结构在鸟撞问题下的动力学响应是研究飞机结构抗鸟撞性能的关键一环。

研究人员对飞机复合材料部件的鸟撞响应进行了研究,一些研究重点关注了鸟类撞击测试的试验方法和表征方法。Hu等[3]使用加速度计、位移传感器和动态应变仪来表征直升机复合驾驶舱对鸟类撞击的响应。Park等[4]使用前缘内表面上的环氧树脂粘合光纤传感器测量了复合材料机受到鸟类撞击时的瞬态应变。Liu等[5]使用明胶射弹进行的气枪试验研究了机织织物碳纤维复合材料的鸟撞冲击性能。

由于飞机结构试件制造成本高、鸟击试验难度大,数值模拟成为研究飞机结构抗鸟撞分析的有效工具。一些数值研究描述了鸟类在撞击过程中的巨大变形,另一些研究则试图模拟复合材料结构的动态失效行为。学者们研究了3种有效的鸟撞模型建立方法,包括任意拉格朗日-欧拉(Arbitrary Lagrangian-Eulerian,ALE)模型[6]、耦合欧拉-拉格朗日(Coupled Eulerian-Lagrangian,CEL)模型[7,8]和平滑粒子流体动力学(Smoothed particle hydrodynamics,SPH)模型[9]。Heimbs[2]发现用状态方程描述鸟体的本构模型,采用SPH方法与试验结果吻合较好。

复合材料的材料模型的建立需要综合各种失效准则。Heimbs等[10]使用正交各向异性线弹性公式和Hashin失效准则来表征复合材料层合板的动态损伤行为。Orlando等[11]使用Chang-Chang准则来表征复合材料机翼襟翼和风扇叶片的损伤行为。Hu等[3]利用Tsai-Hill失效理论预测了直升机复合材料座舱结构鸟撞击反应。Vijaya Kumar[12]使用横向和剪切损伤因子来预测复合材料机头结构中受到鸟类撞击而引起的刚度损失。复合材料失效之前的结构变形通常可以通过上述模型进行预测。在对复合材料的非线性本构和应变率效应的研究上,Johnson等[13]使用Ladeveze的本构模型对复合材料前缘上的鸟类撞击事件进行了建模,该模型通过损伤能量释放率引入了复合材料的非线性行为,仿真结果与试验结果较匹配。Georgiadis等[14]使用双相材料模型模拟了复合材料机翼后缘结构在鸟撞下失效的全局非线性行为。失效应力和损伤参数独立地表征了基体和纤维强度,并且模型正确地预测了中高冲击速度下的损伤。McCarthy等[15]在纤维金属层压机翼前缘结构上模拟了鸟类的撞击。该模型描述了玻璃/环氧树脂复合材料的各向异性应变率效应和非线性损伤行为。模拟的结果显示,鸟体没有穿透边缘蒙皮,与试验测试结果相符。

建立了可以准确描述复合材料力学行为的材料模型后,许多学者对复合材料结构的抗鸟撞行为进行了研究。Hou等[16]使用纤维/环氧树脂系统对复合板进行了鸟撞试验。结果表明,击穿阈值速度和高速冲击下的变形机理共同决定了复合材料的抗冲击性能。Di Caprio等[17]利用经过验证的数值模型来测试具有不同夹心材料和蒙皮厚度的众多前缘的耐撞性。较厚的蜂窝和较薄的蒙皮可以最好地减少变形,防止鸟类穿透。Liu等[18]改进了复合材料垂直尾翼、天线罩后面的盖板和水平尾翼的防鸟撞性能。最佳设计包括纵梁、泡沫填充、变化曲率和三角形加固。优化后结构在不增加重量的情况下提高了抗鸟撞的最大冲击速度。

复合材料结构上的鸟撞行为已被广泛研究。然而,很少有人考虑复合材料的非线性行为和应变率效应。大多数优化工作关注材料和结构形状,忽略堆叠影响。本文根据Long等[19]提出的一种基于ABAQUS的模拟复合结构鸟类撞击行为的数值方法以及纤维增强复合材料非线性行为和应变率依赖性的本构模型,对某民机机头雷达罩的抗鸟撞性能进行研究。实现了面板复合材料铺层顺序以及前后面板厚度比的数值优化。结果有助于大曲率的复合材料结构的耐撞性设计。

1 有限元模型

有限元数值模型的有效性主要取决于本构关系的准确性。本文对鸟撞事件中涉及的每种材料选取了适当的本构模型。本文研究的雷达罩结构由T700/3234碳纤维增强环氧树脂基复合材料、聚氨酯泡沫制成。值得注意的是,泡沫和复合材料在动态载荷下的表现与静态载荷下的表现不同。因此,鸟撞数值模拟中使用的本构模型应考虑材料的应变率效应。本文采用Long等[19]报告的本构模型。Long等在研究机翼前缘的鸟撞响应时,提出了构成前缘的每种材料的本构模型。其中,复合材料模型考虑了非线性行为、应变率依赖性以及不同的失效模式。然后,通过对2种边缘结构的鸟类撞击测试来验证该模型。从动态响应到最终失效特征,2种结构的数值结果都与试验观察结果吻合良好。

1.1 面板材料的本构模型

本文中的雷达罩模型采用泡沫夹芯结构,两层复合材料之间采用泡沫填充,这样不仅可以增强结构的吸能能力,还可以吸收电磁波,使飞机在雷达上隐形[19]。在蒙皮的实际结构中,沿厚度方向的尺寸远小于面内尺寸。同时,类似雷达罩这样的大曲率结构在鸟类撞击过程中,厚度方向的应力可以忽略不计。因此,可以假设复合材料层压板在鸟击期间处于平面应力状态下。此外,由于单向复合材料的纤维沿相同方向放置,该材料可被视为正交各向异性。正交各向异性材料在平面应力情况下的弹性应力-应变关系被用作本构模型的基础,表示为

(1)

E1、E2和G12分别代表纵向弹性模量、横向弹性模量、纵向剪切模量。从不同应变率下的单轴试验结果观察到[20],模量随着应变率的增加而增加。为了表征材料的应变率依赖性,使用幂函数来表达模量和应变率的关系,如下式

(2)

同时,为了描述材料在横向压缩和纵向剪切作用下的非线性力学行为,引入了2个损伤因子

(3)

(4)

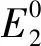
随着损伤的发展,材料失去承载能力后就会发生破坏。对于任意加载方向,当应变达到阈值时,材料承载能力就会突然下降。并且,每种模式的失效应变与应变率无关[20]。因此,Long等[19]为单向复合材料引入了5种失效模式,并且每个方向的失效准则均被定义为失效应变的二次函数

(5)

(6)

(7)

(8)

(9)

其中,式(5)和式(6)分别为沿纤维方向的拉伸破坏和压缩破坏的失效准则,式(7)和式(8)分别为垂直于纤维方向的拉伸破坏和压缩破坏的失效准则,式(9)为纵向剪切破坏的失效准则。

本研究中夹层材料使用的泡沫是硬质聚氨酯,一般被认为是均质各向同性材料,可使用冯·米塞斯屈服准则和各向同性硬化规则的弹塑性模型进行描述。根据已有研究[21],聚氨酯泡沫的屈服应力对应变率有很强的依赖性。为了获得泡沫的机械参数,Long等[19]进行了准静态和动态压缩测试。结果表明,聚氨酯泡沫的加载过程可分为3个阶段:以屈服应力结束的线弹性阶段、具有稳定的应力值的平台阶段和密实强化阶段。随着应变速率的增加,弹性模量以及强化曲线的斜率几乎不变。因此,与应变率相关的唯一变量是屈服应力,可用以下公式描述

(10)

式中:σ0是在0.001/s的参考应变率下的屈服应力,k是通过试验获取的与应变率相关的系数。本文对硬质聚氨酯泡沫的材料参数定义如下:密度ρ=75 kg/m3,弹性模量E=92 MPa,参考屈服应力σ0=1.55 MPa,k=0.23。

1.2 雷达罩及鸟体的有限元模型

本文按照实际尺寸建立雷达罩几何模型,雷达罩采用“三明治”泡沫夹芯结构,即2层复材层中间加入泡沫层并通过Tie连接。基于几何模型、材料参数以及碳纤维增强聚合物复合材料的非线性动力本构,建立鸟撞计算的有限元模型。模型共186 430个单元,其中鸟体和雷达罩泡沫层采用C3D8R单元,分别有2 596个和61 278个;雷达罩面板层采用S4R单元,共122 556个。

本文使用ABAQUS软件提供的Conventional shell模型定义复合材料层合板,如图1所示。根据记录的鸟撞测试视频,鸟类在高速撞击相对刚性的结构时表现出类似液体的行为。本文通过SPH方法对鸟进行实体单元建模。SPH方法是一种基于插值理论和平滑核函数的无网格拉格朗日技术[22],该方法不受网格大变形问题的影响,因此该方法能够较好地描述鸟体剧烈的大变形和飞散现象。现今,大多数与鸟撞问题相关的研究均选用SPH法进行数值模拟。鸟体的有限元模型为两端呈半球状的圆柱体,根据试验的几何尺寸设置。鸟体模型的半球直径为56 mm,纵向总长度为112 mm,如图2所示。

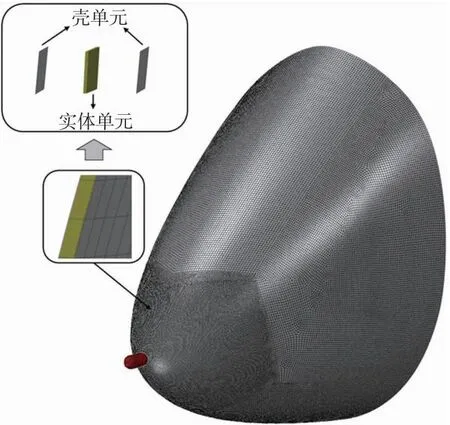
图1 雷达罩有限元模型

图2 鸟体有限元模型

材料属性方面,雷达罩复合材料面板采用复合材料牌号为T700/3234,其材料参数如表1所示。鸟体密度为938 kg/m3,弹性模量为68.9 MPa,泊松比为0.49,屈服应力6.89 kPa,网格尺寸为10 mm。设置鸟体沿航向速度为183 m/s。

表1 T700/3234复合材料单层的力学参数

首先,讨论了面板材料的本构模型对模拟结果的影响,分别对以下4种本构进行模拟鸟撞试验:(1)采用复合材料非线性动力本构;(2)采用线弹性本构与ABAQUS软件内嵌Hashin失效准则;(3)仅考虑复合材料的应变率效应;(4)仅考虑材料的非线性行为。

进而,在同时考虑材料非线性以及应变率效应的框架下,为了分析复合材料铺层顺序对雷达罩吸能的影响,本文对8种铺层顺序进行讨论,如表2所示。

表2 A组工况设置

同时,为了分析前后面板厚度比值对雷达罩吸能的影响,在相同的面板总厚度下,本文对5种不同前后面板厚度比的工况进行分析讨论,为避免出现连续叠置相同铺层角度,取非对称铺层顺序,固定为[90/0/45/-45/0/90],通过改变复合材料的单层厚度达到不同前后面板厚度比,面板厚度设置如表3所示。

表3 B组工况设置

对于鸟撞问题这种极其不连续过程的分析,本文使用ABAQUS/Explicit 进行了显式动态分析,该分析被认为对于分析动态响应时间相对较短的大型模型而言计算效率较高。鸟体在大约0.15 ms时开始首次接触雷达罩,总模拟持续时间为15 ms。

1.3 网格收敛性分析

在鸟撞冲击的模拟过程中,雷达罩模型的网格尺寸往往会对模拟的结果有所影响。一般来说,尤其在受冲击的区域,雷达罩模型的网格尺寸应不大于10 mm,以保证模拟结果的准确性。但同时,越小的网格会带来越多的计算消耗。因此,本文在正式开始模拟试验之前,进行了网格收敛性分析,旨在找到一个能平衡计算效率和计算精度的网格尺寸。本文对5～80 mm区间内的模型全局尺寸进行试验,以鸟体动能作为量化指标,结果如图3所示。

图3 不同网格尺寸下的鸟体动能-时间图

由图3可知,网格尺寸达到20 mm时会进入收敛状态,为了确保计算的准确性,本文对鸟体撞击区域的雷达罩模型采用10 mm的网格尺寸,和鸟体网格尺寸保持一致,对撞击区域之外的模型采用20 mm的网格尺寸,如图1所示。这种网格尺寸的分层设计旨在对有大变形的区域使用更细的网格以保证计算精度,防止网格出现畸变,而外层的较大尺寸的网格可以让计算效率维持在一个合理区间。

2 结果与讨论

2.1 非线性效应及应变率效应对雷达罩鸟撞响应的影响

首先对采用的考虑非线性和应变率效应的本构模型进行讨论。Hashin准则作为一种经典的复合材料失效准则,其适用范围是广泛的。然而,在考虑鸟撞这类强冲击问题时,Hashin失效准则模型对这种高应变率下复合材料结构损伤破坏行为描述便不够准确。因此,本文采用了Long等[19]提出的非线性本构模型对碳纤维增强复合材料雷达罩模型进行描述。同时,该本构模型还考虑了材料的应变率效应,进一步增强了本构模型的适用性和准确性。

如图4所示,在铺层顺序均为[90/0/45/泡沫/-45/0/90]、前后面板厚度均为0.3 mm的情况下,分别考虑以下4种本构模型:(1)同时考虑非线性和应变率效应;(2)仅考虑应变率效应;(3)仅考虑非线性;(4)非线性和应变率效应均不考虑。结果显示,仅在同时考虑非线性和应变率效应的工况中,模型能出现与试验结果吻合的大变形模式[19-21]。图4(a)中的雷达罩模型在受到鸟体撞击后,发生大变形凹陷,面板中的复合材料发生损伤出现非线性力学行为,泡沫材料快速进入塑形阶段进行吸能,最终鸟体未能击穿雷达罩。而图4(b)～(d)中的雷达罩模型在受到鸟体撞击后,应力状态在数毫秒内达到失效条件发生破坏,表现为鸟体迅速击穿雷达罩并威胁到后部结构,这种现象显然是不符合试验真实表现的。鸟撞问题是典型的高速大变形问题,对于高速问题,考虑材料的应变率效应是必要的;而对于大变形问题,考虑材料的非线性是必要的,这也解释了为什么非线性和应变率效应缺一不可,只有采用同时考虑材料非线性和应变率效应的本构模型,才能较为准确地描述这一类问题。

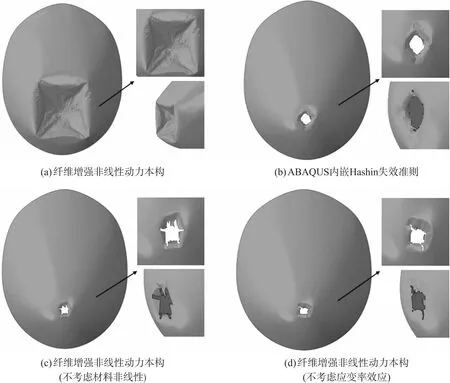
图4 不同复合材料本构下雷达罩受鸟撞后变形图

本文还考虑泡沫的应变率效应对结构破坏模式的影响,如图5所示,图5(a)为考虑泡沫应变率效应的泡沫层失效情况,图5(b)中的模型仅设置了泡沫的塑性应变,不考虑应变率效应。由图5可以发现泡沫层失效情况稍有不同,在考虑应变率效应的工况中,应力集中在破坏面的角落位置,而对于不考虑泡沫应变率效应的模型来说,应力集中区域分散在破坏边缘。此外,考虑应变率效应的泡沫层的最大Mises应力达到了2.81 MPa,而不考虑应变率效应的模型仅有1.63 MPa。相对而言,考虑应变率效应的模型的最大Mises应力比不考虑应变率效应的模型高42.3%。

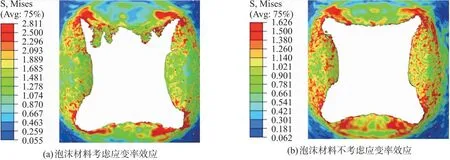
图5 雷达罩面板泡沫层应力云图

2.2 面板复合材料铺层顺序对抗鸟撞性能的影响

在验证了面板复合材料的非线性动力本构的有效性和必要性之后,本文对面板复合材料的铺层顺序进行了研究和讨论。如表2所示,A组的8个工况分别对应不同的铺层顺序。计算结果如图6～10所示。

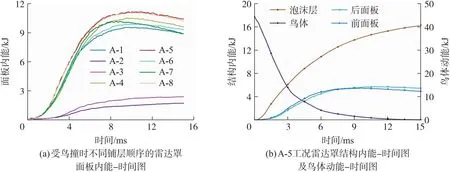
图6 受鸟撞时不同铺层顺序雷达罩面板及最优工况结构内能-时间图和鸟撞动能-时间图

图6统计了雷达罩面板的内能随时间变化的曲线图。在鸟撞问题中,若雷达罩被击穿,鸟体动能主要转化为结构的内能和鸟体剩余动能,此时鸟体剩余动能越小说明结构抗鸟撞能力越强;当雷达罩未被击穿时,结构的内能越高则说明结构的抗鸟撞能力越强[23]。对于A组工况而言,8个工况的雷达罩全部被击穿,因此在图5中,雷达罩面板的内能越高,证明该结构的吸能效果越好,对后部结构的保护作用越强。如图6(a)所示,A-2和A-3工况的吸能效果是最不理想的,这是因为A-2和A-3的铺层顺序分别为[45/45/45]/[45/45/45]和[-45/-45/-45]/[-45/-45/-45],不仅前后面板的铺层方向一样,面板内部的3层复合材料的铺层材料也均相同,这是最为极端的不理想情况。若连续叠置相同铺层角度,会降低结构的最大屈曲载荷,减少对能量的吸收。因此,这2个工况的表现极差,仅能吸收1～2 kJ左右的能量,面板能量吸收率低于5%。除此之外,其余工况均表现出相同的变形模式和吸能行为。在0～8 ms内,结构的内能迅速从0增加到9～11 kJ,同时,鸟体动能从44 kJ迅速下降至2.4 kJ,面板能量吸收率达到20%～25%。在6个工况之中,A-5和A-8工况的吸能效果最好,在8 ms时结构内能均达到了11 kJ。A-5工况的铺层顺序为[0/-45/45]/[45/-45/0],前后面板呈对称交叉排列;A-8工况的铺层顺序为[0/-45/45]/[-45/45/0],铺层角度交叉排列。这种排列方式有助于复合材料发挥其各向异性的优异性能,尤其是对于纤维增强复合材料而言,交叉排列的铺层顺序能保证面板结构没有一个明显的弱方向,进而能更好地承受实际情况中各种不同的极端应力状态。在图6(b)中,本文对A-5工况中雷达罩各个铺层的吸能效果进行分析。总体而言,鸟体的动能在13 ms内被完全吸收,而面板材料中吸收能量最多的是夹芯泡沫层,面板和芯材发生耦合作用,导致其排列对称、厚度相同的前后复合材料面板吸收能量基本相同。

高速冲击会对复合材料基体和纤维造成损坏,其中纤维断裂可能导致复合材料层压板的整体失效。图7～10比较了8种不同铺层顺序和角度的复合材料面板的损伤模式。从蓝色到红色表示从未损坏(弹性)到最大损坏(失效)的损坏状态。如果某个单元的损伤因子等于1,则该元素已失去其承载能力并发生破坏。

图7 A-1～A-8工况的纤维压缩/拉伸损伤图

复合材料夹层结构包括前面板和后面板损坏。图7描述了A-1～A-8工况前后面板的纤维拉伸损伤和纤维压缩损伤。据观察,前后面板的损伤模式基本一致,初始撞击区域为高损伤区域,随后以不同的模式向周围传播,传播模式与铺层顺序和纤维排列方向有关。纤维拉伸和压缩的损伤模式类似,无明显区别。由于夹心泡沫层吸收了很大一部分能量,从而使得后面板的损伤程度普遍较轻,但损伤的分布还是与前面板一致。A-2和A-3工况作为纤维方向排布最不合理的2个工况,面板的损伤是最小的,吸收的能量也是最低的,由于纤维方向排布一致,考虑材料非线性和应变率效应的情况下,雷达罩变形模式明显不同于其他几种工况。所以这2个工况的鸟体能量主要有泡沫夹芯层吸收,从而使前后面板的损伤不明显。

图8描述了雷达罩面板复合材料基体的损伤行为。从图中可以看出,同一工况前、后面板的损伤模式依然相似,拉伸、压缩的损伤也遵循同一个模式。然而,对于基体材料而言,拉伸损伤的程度和范围比压缩损伤要严重。基体损伤的发展路径规律与纤维损伤的发展模式相似,都会在初始撞击区域产生最严重的损伤区,然后在铺层顺序和纤维方向的共同影响下演化出不同的损伤发展路径。

图8 A-1～A-8工况的基体压缩/拉伸损伤图

2.3 面板复合材料层厚比对抗鸟撞性能的影响

除了不同铺层顺序以及铺层角度的面板外,本文还对具有相同总厚度,不同前、后面板层厚比的面板的雷达罩模型进行研究。复合材料层共6层,厚0.6 mm,在先前的研究中,前后面板的复合材料层数是相等的,即各有3层复合材料,厚0.3 mm。在本节中,对复合材料层进行重新分配,B-1～B-5工况分别对应着具有1至5层复合材料的前面板,相应的,后面板的复合材料层数为5至1层,故前、后面板层厚比为0.2、0.5、1、2和5。复合材料总层数控制在6层,总厚度控制在0.6 mm,与前文保持一致,具体设置见表3。

图9为B-1～B-5工况受鸟撞时雷达罩面板内能随时间变化的曲线图,与图6(a)类似,面板内能越大意味着其吸收能量越多,结构的抗鸟撞性能越好。不难发现,前后面板厚度相等的B-3工况拥有最好的吸能能力,可以吸收10 kJ的鸟体动能,层厚比为2的B-4工况以及层厚比为0.5的B-2工况次之,且发现层厚比为2的B-4工况比层厚比为0.5的B-2工况多吸收近2 kJ的能量,说明在总厚度不变的情况下,前面板较厚工况比后面板较厚工况的吸能情况要好。极化分布的B-1和B-5工况吸能表现最差,仅能吸收6 kJ左右的能量,并且由图可知,当层厚比越接近1时,前后面板吸能越多,抗鸟撞性能越好。但是,B-1和B-5工况的响应是最快的,在2 ms的时候已经吸收了3 kJ的能量,是该面板能吸收的总能量的50%,而同时期的其他工况仅吸收了1 kJ的能量。

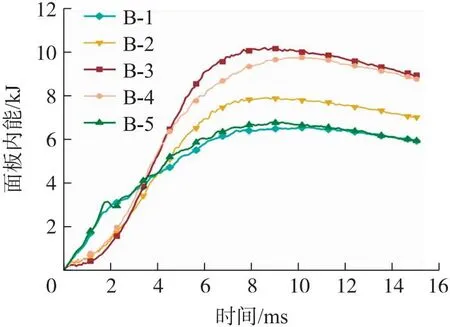
图9 受鸟撞时不同层厚比的雷达罩面板内能-时间图

图10描述了B组所有工况下与泡沫芯材相邻的前面板和后面板的基体压缩损伤。据观察,面板的厚度分布对不同配置的复合材料的基体压缩损伤有显著影响。复合材料层极化分布的B-1和B-5工况的损伤情况较另外3种工况明显更为严重,材料有更大的可能发生破坏。

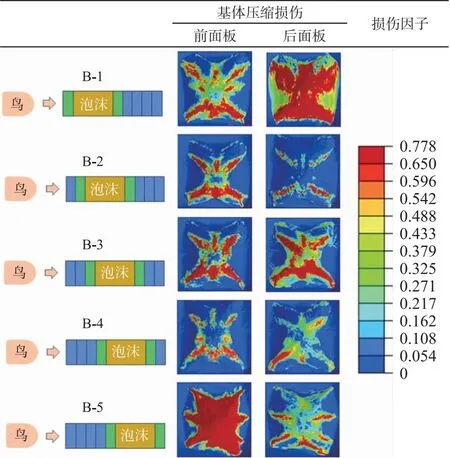
图10 受鸟撞时不同层厚比的雷达罩面板复合材料基体压缩损伤图

可以观察到,与泡沫芯材相邻的前后面板,B-1工况的后面板和B-5工况的前面板是损伤最严重的,即越厚的面板,其靠近芯材的复合材料单层的基体压缩损伤越严重,即在这种极端情况下,最中间铺层所受基体压缩破坏最严重。

2.4 面板复合材料铺层角度和层厚比对结构最大挠度的影响

除了材料的损伤之外,雷达罩的最大挠度也是本文关心的指标。当雷达罩的变形过大时,即使材料本身没有破坏、鸟体没有直接击穿雷达罩也会影响后续结构,雷达罩自身过大的变形仍然有可能致使后续结构发生变形和位移,影响部件的正常工作。对于拥有不同复合材料铺层角度的A组工况来说,结果如图11所示,不同铺层顺序前后面板最大挠度值相差不大,前面板比后面板多3～4 mm。2种叠置相同铺层工况A-2、A-3的挠度值最大在1 350 mm左右,明显大于其他工况;3种对称排布工况A-1、A-4、A-6的面板最大挠度值在1 030 mm左右;2种非对称排布工况A-7、A-8的面板最大挠度值在992 mm左右,是所有工况中最小的。该结果说明连续叠置相同铺层角度会导致过大挠度值出现,非对称排布工况的最大挠度值要稍低于对称排布工况。

图11 不同铺层顺序前后面板最大挠度值对比

复合材料面板的吸收内能越多、最大挠度值越小说明该工况的抗鸟撞性能越好,为了更直观地对比出不同工况的抗鸟撞性能,本文对前后面板吸收最大内能和出现的最大挠度值分别进行了如下处理,用单个数据与均值的差值除以均值,得到影响因子(Impact factor,IF)

(11)

以吸收内能为例,IF值为正且值越大,说明该工况下面板吸收内能高于平均吸收内能,在这8种工况中表现的抗鸟撞性能较好;最大挠度值则与内能相反,IF值为负且值越小,说明该工况下最大挠度值低于平均最大挠度,表现的抗鸟撞性能越好。

需要说明的是,本文用IF值的大小来对比这几种工况的抗鸟撞性能,在图12当中,将与挠度相关的IF值取负处理,保证IF值为正且越大,其抗鸟撞性能在这8种工况中越好。如图所示,处于蓝色区域说明抗鸟撞性能高于平均值,处于红色区域说明低于均值。

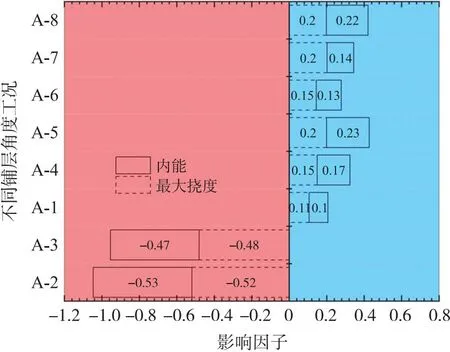
图12 不同铺层角度对雷达罩面板内能及最大挠度的影响

根据图12,可以清楚地知道A-2、A-3叠置相同铺层工况的抗鸟撞性能最差,其他非叠置相同铺层的工况中,无90°铺层的A-5、A-8工况对比有90°铺层的A-1、A-4、A-6和A-7工况的抗鸟撞性能较好。

对于拥有不同前后面板层厚比的工况来说,结果如图13所示,对比B-1和B-5这2种层厚比低于0.5或者大于2的情况,其最大挠度值明显低于其他工况,说明层厚比对最大挠度值有较大的影响。B-5工况的前后面板最大挠度值为902.3 mm和904.58 mm,明显低于其他4种工况,且由于前面板厚度是后面板的5倍,导致其前面板最大挠度值低于后面板,这是与其他所有工况都不同的;B-1工况前后面板最大挠度值为953.88 mm和951.56 mm,比B-5工况多了约51 mm。

图13 不同层厚比前后面板最大挠度值对比

对比B-2、B-4和B-3工况,层厚比为1时,最大挠度值低于其他2种;B-4工况最大挠度值为1 008.24 mm,低于B-2工况的1 011.41 mm,说明增厚前面板,会降低面板的最大挠度。

由图14可知,层厚比为0.5的工况抗鸟撞性能最差,吸收内能和最大挠度均处于红色区域;层厚比为1和5的工况抗鸟撞性能最好,层厚比为0.2和2的工况次之。综合上文对面板损伤情况的评估,可知,层厚比接近1的工况是抗鸟撞性能最优的。

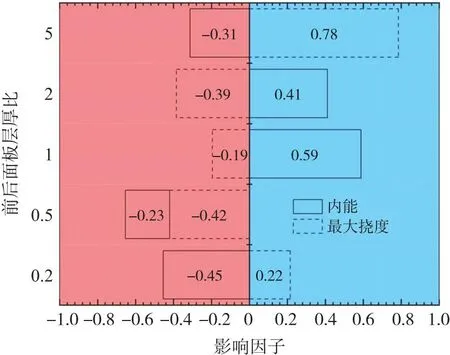
图14 不同前后面板层厚比对雷达罩面板内能及最大挠度的影响

3 结论

本文通过有限元方法,采用纤维增强非线性动力本构对复合材料的力学行为进行描述,对某民航客机的雷达罩的鸟撞问题进行了探究。本文主要对纤维增强复合材料板的铺层顺序和角度,以及层厚比进行讨论,具体结论如下:

(1)运用ABAQUS的VUMAT子程序,实现了二维平面应力状态下的纤维增强非线性动力本构模型的数值方法应用。并通过数值模拟,和不考虑材料非线性、应变率效应本构的对比,验证了纤维增强非线性动力本构模型对鸟撞雷达罩的模拟更加精确。

(2)分析了运用纤维增强非线性本构的雷达罩前后面板的层内损伤因子图,发现在不同铺层角度下,其破坏形式基本相同,面板最主要的失效形式是基体拉伸破坏,纤维拉伸、压缩破坏情况基本相同,而对于基体材料,拉伸破坏远比压缩破坏更加严重。

(3)对比了不同层厚比面板对抗鸟撞性能的影响,发现层厚比越接近1,即前后面板厚度一致时,面板吸收能量越多,其次是前面板较厚的工况;当面板层厚比低于0.5,或者大于2时,面板吸能最差。

(4)对比了不同铺层角度和不同层厚比对面板最大挠度的影响,发现非对称铺设工况的最大挠度值小于对称铺设和叠置相同角度的工况;对于不同层厚比工况,发现层厚比值越偏离1时,最大挠度值越小。