ECM重塑下肿瘤淋巴管生成模型的定性分析与数值模拟

王振友，黄亚婷

（广东工业大学 数学与统计学院, 广东 广州 510520）

肿瘤是一种严重危害人类生命健康的疾病，特别是恶性肿瘤。近年来，许多学者开始关注肿瘤生长、转移和微环境等相关问题，尤其是在了解肿瘤转移的机制并提供有效治疗策略方面，数学建模成为重要的研究手段之一。肿瘤转移是癌症发展过程中的关键环节，也是治疗失败和恶化的主要原因之一[1]。

肿瘤淋巴管是肿瘤中新形成的血管(tumor angiogenesis)，为肿瘤提供营养和氧气，被认为是与肿瘤转移和发展有关的重要因素之一[2]。淋巴管在正常情况下是通过一系列复杂的反应和信号来生成的，但在肿瘤中肿瘤细胞释放特殊的生长因子和化学信号物质，诱导周围的血管和淋巴管内皮细胞增殖和分化，形成新的淋巴管网络[3]。研究肿瘤淋巴管生成对于了解肿瘤的生长、转移和治疗具有重要意义。通过阻断肿瘤淋巴管生成，可以抑制肿瘤的生长和转移，并提高现有抗肿瘤治疗的效果。

在肿瘤淋巴管生成中，内皮细胞生长因子(Vascular Endothelial Growth Factor, VEGF)和细胞外基质(Extracellular Matrix，ECM)重塑是关键因素之一。VEGF在肿瘤发展中起着重要作用，高表达的VEGF与肿瘤的恶性程度和淋巴管生成密切相关[4]。ECM重塑则为肿瘤细胞的转移和淋巴管生成提供了条件[5]。VEGF作为一种主要的血管生成因子，已被广泛研究和证实其在血管新生和肿瘤转移中的作用。先前的研究表明，VEGF是肿瘤淋巴管生成的重要调节因子之一，实验证实干扰VEGF可以有效抑制肿瘤生长和淋巴管生成[6]。曹雪涛院士等[7]的研究综述中指出，肿瘤转移微环境对VEGF的产生和释放具有重要的调节作用，以及和ECM重塑等多方面的协同作用。此外，在过去的几十年里，前人研究中提到基质降解酶(Matrix Metalloproteinases，MMP)也是ECM重塑的一个关键成分[8]。

以往的数学模型主要关注肿瘤生长规律，而忽略了基于肿瘤转移各组分间的相互作用[9-10]。为了更准确地描述肿瘤淋巴管生成过程，本文提出了一个考虑ECM重塑的模型，并且考虑了MMP对肿瘤淋巴管生成的影响。此外，VEGF作为关键的血管生成因子，在模型中起着重要作用。研究发现肿瘤转移微环境对VEGF的产生和释放具有调节作用，这进一步说明了VEGF在肿瘤淋巴管生成中的关键性。

1 数学模型及方程

上述考虑肿瘤转移过程中的ECM重塑作用，针对微环境中各种涉及肿瘤淋巴管生成的成分进行建模。至此，用流程图来描述本文提出的模型机制(见图1)，由图1可知，内皮细胞的趋化性作用由内皮细胞生长因子VEGF引起。内皮细胞生长因子由肿瘤细胞和ECM分泌，MMP由肿瘤细胞和内皮细胞分泌，MMP的作用是降解ECM。内皮细胞和MMP的趋触性由ECM引起，内皮细胞和MMP会向ECM发生微小转移。

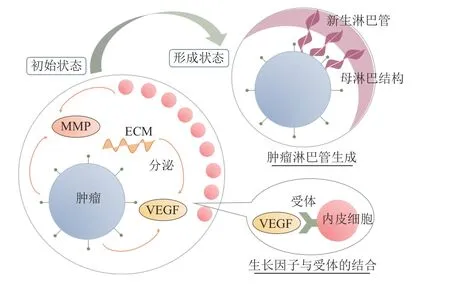
图1 肿瘤淋巴管生成模型示意图Fig.1 Schematic diagram of generative model of tumor lymphatic vessels

为了建立肿瘤转移微环境的模型，需要对肿瘤淋巴管生成的机制进行数学描述。本文总结在肿瘤淋巴管生成过程中的主要参与成分，并进行各个因素和变量的确定。根据上述肿瘤淋巴管生成机制的表述，这里设定相关成分：m为 ECM的浓度，n为肿瘤细胞的浓度，c为内皮细胞的浓度，s为淋巴管内皮细胞生长因子VEGF的浓度，q为基质降解酶MMP的浓度。

不同因素之间存在相互作用和调节关系，共同影响和塑造了肿瘤淋巴管生成的环境。因此，本文可以考虑各成分之间作用关系的数学表达，以描述它们之间的相互作用和调节关系。

式中：t为时间，σ 为MMP降解系数。

(2) 肿瘤细胞会发生增殖和扩散，还会分泌内皮细胞生长因子。因此肿瘤细胞的浓度方程为

式中：等号右边第1项为肿瘤细胞的扩散，Dn为肿瘤扩散系数；右边第2项为肿瘤细胞的增殖，λ 为肿瘤增殖系数，n0为 肿瘤细胞初始浓度，nM为肿瘤细胞增殖上限；右边第3项为肿瘤细胞的死亡， μn为肿瘤细胞死亡系数。

(3) 内皮细胞会发生扩散，并且会对VEGF的刺激发生趋化运动，内皮细胞的受体会与VEGF相结合，另外内皮细胞还会向ECM转移，帮助形成淋巴管结构。内皮细胞的方程为

式中：等号右边第1项为肿瘤细胞的扩散，Dc为内皮细胞扩散系数；右边第2项为内皮细胞受到VEGF的刺激发生的趋化运动项， θ,ρ为相关激活和趋化系数；右边第3项为内皮细胞向ECM的转移项， χc为内皮细胞转移系数；右边第4项为肿瘤细胞的死亡，μc为肿瘤细胞死亡系数。

(4) VEGF由肿瘤细胞和ECM分泌，会与内皮细胞相结合，并且还会发生扩散。VEGF的浓度方程为

式中：等号右边第1项为肿瘤细胞的扩散，Ds为VEGF扩散系数；右边第2、3项为肿瘤细胞和ECM分泌VEGF项， αs,βs分别为肿瘤分泌VEGF系数和ECM分泌VEGF系数；右边第4项为内皮细胞吸收项，φ 为内皮细胞与 VEGF作用的吸收系数。

(5) MMP由肿瘤细胞和内皮细胞分泌，并发生扩散，并且向基质转移降解ECM。MMP的浓度方程为

式中：等号右边第1项为肿瘤细胞的扩散，Dq为MMP扩散系数；右边第2项为MMP向ECM转移项，χq为 MMP转移系数；右边第3、4项为分泌项，αq,γq分别为肿瘤分泌MMP系数和内皮细胞分泌MMP系数。

本文提出一个模型来研究肿瘤淋巴管生成中VEGF的影响。在建立模型之前，基于以下假设：

(a) 假设VEGF是肿瘤淋巴管生成的关键因素之一，其高表达与淋巴管生成的增加密切相关。VEGF的表达受到多个因素的调控，如肿瘤细胞内部信号通路的激活以及外部环境因素的影响，本模型仅考虑VEGF与内皮细胞受体结合后生成淋巴管结构的情况。

2 预备知识

下面将介绍一些需要用到的引理和记号。首先，本文引入一些记号：

式中：

下面介绍一些有用的引理。

引理1[11]假设D是一个正常数，a(x,t),b(x,t)是区间 ΩT连 续有界函数，函数f(x,t)∈Lp(ΩT)，φ ∈C1[0,T]，且对1 ＜p＜∞ 有u0(x)∈DP(0,L) 。 令其中(1) α =0，β=1； (2) α =1，β ≥0，初值问题

3 局部解的存在唯一性

显然度量空间 (XM,d)是一个完备的度量空间，对于∀u∈XM，定义一个映射u→～u，式中～u=F(u)满足如下问题：

类似地可以得到问题(5)结论为

取T＞0 充分小，使得0 ＜η(T)C(T)＜1， 此时F为XM上的压缩映射。由Banach不动点定理可知，当T＞0 充分小时，F存在唯一的不动点(m,n,c,s,q)，是问题(6)～(10)在区域 ΩT中的唯一解。由证明过程可知T依赖于初值m(x,0),n(x,0),c(x,0),s(x,0),q(x,0)在空间C2+α(0,L)中的范数的上确界。上述结果可以整理为定理1。

定理1 存在T＞0 ，对所有t∈[0,T]，原问题(1)～(5)的逼近问题(6)～(10)在区域ΩT内存在唯一的解 ，其中T依赖于m(x,0),n(x,0),c(x,0),s(x,0),q(x,0)在C2+α(0,L)中的范数的上确界。

4 整体解的存在唯一性

引理4 对式(1)～(5)有结论：0 ≤n≤nM， 以及m,c,s,q≥0成立。

证明 对式(2)应用极值原理可得

同理对于问题(1)、(3)、(4)、(5)中的变量X，应用极值原理可得

则有m,n,c,s,q≥0成立。引理4得证。

引理5 对任意1 ＜k＜∞ ，存在一个依赖于T的常数Ck(T)满足

则‖(c+q)‖Lk+1(ΩT)≤Ck(T) ， 又c≥0,q≥0，则

引理5得证。

引理6 对任意1 ＜p＜∞ ，存在一个依赖于T的常数Cp(T)满足

由引理5可知

且ac(x,t),aq(x,t)是连续有界函数，由引理1 可得‖c‖Wp2,1(ΩT)≤Cp(T),‖q‖Wp2,1(ΩT)≤Cp(T)，引理6得证。

由定理1可得解的局部存在性，由引理7可得解的有界性，基于解的有界性，进而可以得到如下定理：

定理2当条件(b)成立时，任何t＞0时，模型(1)～(5)存在唯一的全局解。

5 数值模拟

为了更直观地体现模型中各成分的关系，本文考虑用差分数值方法求解偏微分方程组(1)～(5)，包括二阶中心差分和一阶前后差分。为了说明简单，考虑无量纲化的数值模拟，这里设定模拟区域在[0,50]×[0,50]网 格中，时间步长为 0.1， 空间步长为 0.5。

相关参数值为[17]：m0=n0=c0=s0=q0=1,Dn=1×10-7,Dc=1×10-5,Ds=1×10-2,Dq=1×10-3,χc=5,χq=7,μn= 0.7,μc=10,θ = 9×10-3,δ = 9×10-7,λ=5,nM=50,φ=0.3,αs=βs=αq=γq=7×10-8。

通过参数调整和数值方法求解，本文得到了从t=0.1到t=0.5肿瘤淋巴管生成的5种成分浓度变化的模拟结果对比，如图3所示。

从图3可以看出，随时间从t=0.1 到t=0.5：(1)ECM受到MMP降解作用局部出现波动；(2) 肿瘤细胞持续发生扩散增殖；(3) 内皮细胞由于趋化和发生转移而减少，局部呈现凹凸峰错叠状；(4) VEGF由ECM和肿瘤细胞分泌而增多，受到内皮细胞吸收而减少，局部出现波动；(5) MMP由肿瘤细胞和内皮细胞分泌而增多，向ECM发生转移而减少，局部也呈现凹凸峰错叠状；此外还包括有些成分的死亡消减等。由此，通过数值实验验证了本文所建立的模型符合如图1所示的生物原理和如图2所示的建模原理，是可靠和准确的，从数学层面反映了主要影响肿瘤淋巴管生成的各成分的变化。

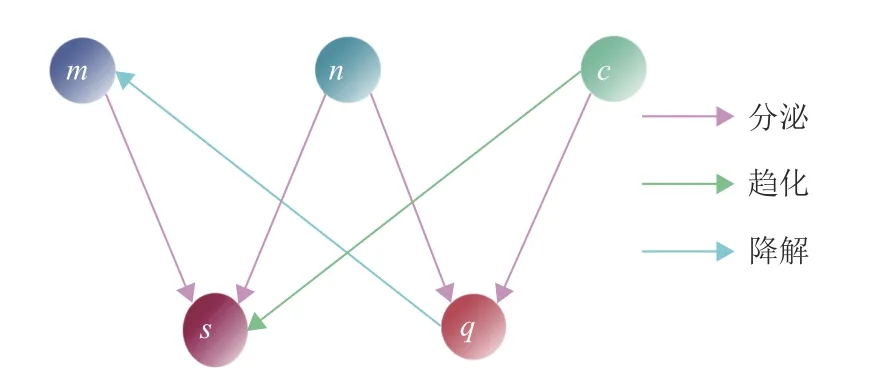
图2 关键因素及其相互关系示意图Fig.2 Schematic diagram of key factors and their interrelationships

图3 从t =0.1到 t =0.5各成分的浓度变化图Fig.3 Concentration variation diagram of each component from t =0.1 to t=0.5

6 结论与展望

相较于以往关注肿瘤生长规律的模型，本文在考虑了肿瘤与ECM相互作用的基础上，建立了一个新的肿瘤淋巴管生成模型。本文考虑了多种成分的相互影响，包含肿瘤生长情况以及ECM重塑和肿瘤淋巴管生成的数量情况。通过对该模型进行理论分析，证明了局部解和整体解的存在唯一性，并通过数值模拟验证了模型的可靠性和准确性。

这项研究对于更深入地理解肿瘤转移机制，指导癌症治疗，并推动相关研究的发展具有重要意义。未来，将进一步探索该模型在不同肿瘤类型和治疗方案中的应用，例如关键因素如何影响肿瘤转移等，并进一步优化模型以提高其预测能力和临床实用性，使其更符合真实的生物学环境。