不同晶面应变纤锌矿GaN/AlN量子阱的价带结构理论研究
刘亚群,李希越,章国豪
(1.广东工业大学 信息工程学院, 广东 广州 510006;2.广东工业大学 集成电路学院, 广东 广州 510006)
纤锌矿氮化镓(GaN)及其异质结构由于具有众多优异的性能,如高导热性、高击穿场以及高电子迁移率等,在高功率电子器件与射频电子学等领域中具有重要的应用前景[1-2]。然而,GaN较大的空穴有效质量导致了低空穴迁移率,阻碍了其在大功率转换器及互补逻辑电路[3]上的广泛应用。对于电力电子学和射频电路的新应用领域,迫切需要一种与N通道GaN高电子迁移率晶体管对应的P型晶体管,以形成宽带隙互补金属氧化物半导体。随着GaN外延生长技术的进步,众多研究机构争相对GaN异质结制备技术开展研究,并通过理论建模探索GaN空穴输运性能的优化方案[4-6]。
GaN的极化效应极大地影响了其空穴的输运性能。通常的GaN外延及其异质结构是在(0001)晶面生长的,即Ga极性面。由于较大的自发极化及应变诱导产生的较大压电极化,AlGaN/GaN异质结构界面处出现高密度的二维电子气[7]。与之类似,在GaN/AlN界面上也会形成二维空穴气[8]。这对于高功率器件和耗尽型器件的生产非常有意义,但对GaN异质结光电器件产生了负面影响,同时GaN基增强型器件的制造有一定难度[9]。通过生长非极性(1 01¯0)及半极性(1 01¯2)晶面,GaN可以避免极化效应的影响。目前,已有文献研究这两类晶面材料的外延生长及其性能[10-11]。尽管对晶面半导体有较多研究,但晶面对GaN基本物理性能的影响还需进一步探究。
此外,研究表明应力可以有效地改变能带结构,这为评估能带色散以及有效质量在应力下的变化提供了一种简单且实用的方法。Poncé等[12]发现,在(0001)晶面上施加2%的双轴拉伸应变,可使自旋-分裂带能量位于重空穴带和轻空穴带之上,使块体GaN的空穴迁移率明显增加。文献[13-14]也研究了单轴应力对GaN空穴有效质量的影响。但上述建模工作主要针对在(0001)晶面的块体GaN,有关GaN异质结量子阱完整结构模型仿真的文献较少。
为了研究应力对不同晶面GaN异质结量子阱性质的影响,本文基于六带k·p方法和自洽薛定谔-泊松方程,并考虑极化效应,研究了(0001)、(1 01¯2)与(1 01¯0)晶面的纤锌矿GaN/AlN异质结量子阱在应力下的二维价带子带结构,给出了空穴有效质量在双轴和单轴应力下的变化关系,探讨P型GaN工作性能的优化方案。
1 理论模型
根据Chuang等[15]的报道,[0001]方向(c-轴)生长的应变纤锌矿晶体包括自旋轨道相互作用的完整哈密顿量H可以表示为
其中矩阵元素为:
式中: Δ1对应于晶体场分裂能量( Δcr),Δ2和 Δ3解释了自旋轨道分裂能( Δso)的相互作用;ki(i=x,y,z)表示波矢,Ai(i=1~6)上的价带有效质量参数,与闪锌矿晶体中的Luttinger参数类似;Di(i=1~6)为Ai相应位置上的纤锌矿晶体的形变势; ϵij(i,j=x,y,z)为应变张量;ℏ 为约化普朗克常数;m0为电子有效质量。
为了探索沿非极性和半极性晶面生长的纤锌矿GaN的显著特征,本文利用(0001)晶面的k·p哈密顿矩阵通过旋转矩阵获得了任意晶面的矩阵[16]。如图1所示,欧拉角θ和φ的旋转将物理量从z(对应于c轴[0001])方向转换为z′方向(对于任意[hkil]晶向)。在旋转参考框架中,新的自旋基矢量为
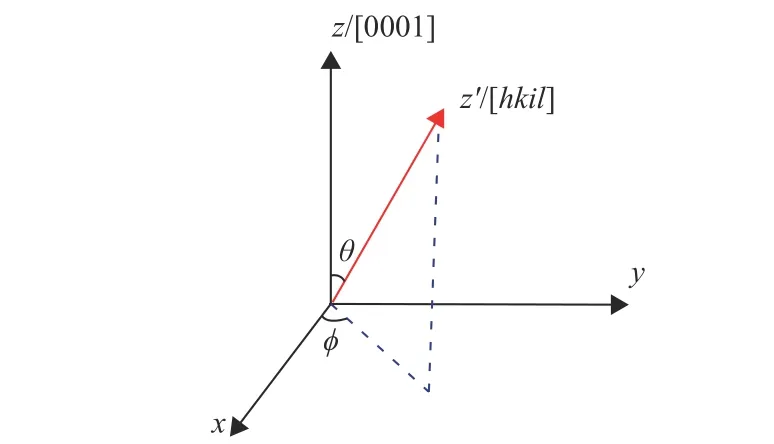
图1 本文中描述的坐标系示意图Fig.1 Schematic diagram of coordinate system described in this paper
旋转矩阵为
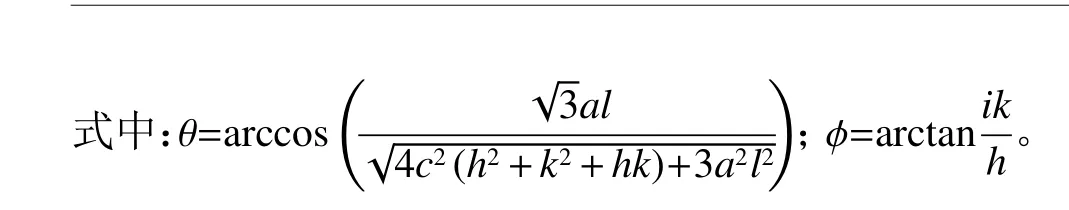
由于GaN晶体具有六重对称性,本文只考虑以下物理量的θ依赖性(即规定φ=0)[17]。从基态(x,y,z)坐标转换为(x′,y′,z′)坐标是通过旋转角度θ来完成的。如图2所示,非极性平面是垂直于c平面的晶体平面,极化矢量位于生长平面。半极性平面与c平面以一定角度相交。在轴的旋转下,向量的分量由式(5)给出:任意晶面的k·p哈密顿量可导出为
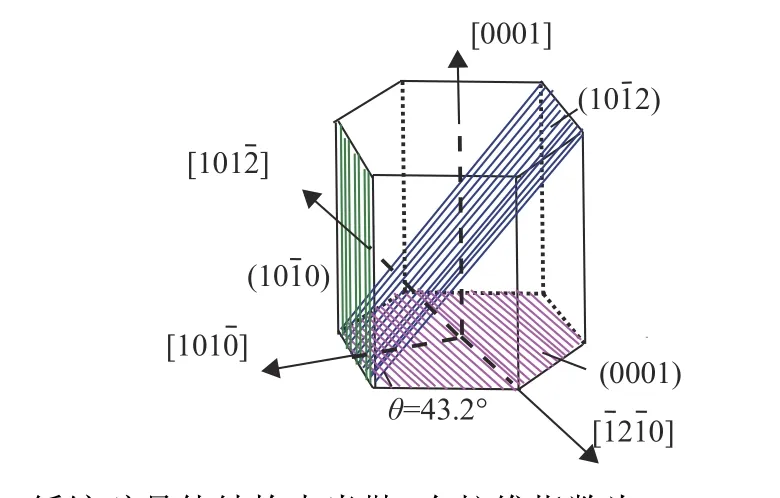
图2 纤锌矿晶体结构中米勒-布拉维指数为(0001)、(1 01¯2)和(1 01¯0)的晶体生长平面的完整示意图Fig.2 The complete schematic diagram of the crystal growth plane in wurtzite crystal structure with Miller-Bravais indices of (0001) , (1 01¯2 ) and (1 01¯0)
其中U为变换矩阵[18],上标* 和T分别表示复共轭和转置。
通常,由于晶格失配,GaN/AlN异质结界面上将产生双轴应力。对于在[hkil]方向生长的应变纤锌矿GaN晶体,应变张量ϵij与倾角θ相关[19],如式(7)所示。
式中:cij是GaN层的弹性刚度常数,a和c是晶格常数,下标s和e分别表示AlN层和GaN层。
本文假设当考虑弛豫AlN上的GaN时,可以忽略AlN衬底,只使用应力分量描述来自衬底的影响。由于GaN的晶格常数小于AlN,所以受到压缩应变的影响,此时,GaN层中同时存在本身固有的自发极化(Psp)和应变诱导的压电极化(Ppz)。参考文献[20],设置AlN厚度为400 nm,GaN层厚度为13 nm,如图3所示,其中点线与界面的电流通道厚度假定为2 nm。生长平面沿(x′,y′,z′)坐标的极化P′可以根据(x,y,z)中的极化矢量P和倾角θ计算得出[21],计算公式为沿(x,y,z)坐标的应变诱导的极化分量Px,Py和Pz的计算公式为

图3 GaN/AlN量子阱示意图Fig.3 The schematic of the GaN/AlN quamtum well
dij是GaN层的压电常数。本文中,只考虑平行于量化方向的压电极化分量。对于量子阱内场(Ez)的计算,可以根据高斯定律确定[22]。
式中:ε是GaN层的相对介电常数,ε0是真空的介电常数。
采用文献[23]中的方法来计算价带子带结构,即基于六带k·p包络函数理论自洽求解薛定谔-泊松方程。计算了Γ点附近的约束带结构,即k< 0.3(2π/a),其中a为晶格常数。在这里,以(0001)极性晶面为例做简要介绍。(0001)输运面上的垂直场产生的量子阱,kz方向被量子化,其可被视为一个算子 (ℏ/i)(∂/∂z),需求解的薛定谔方程为
式中:H(kp,kz) 是价带极值附近的k·p哈密顿量,I是6×6单位矩阵,ψ(z) 是与特征值E(kp) 对应的六维包络函数,kp是二维平面内分量(kx,ky) ,U(z) 为局域密度近似下内场影响下的空穴势能Vp(z) 和交换相关势Vxc(z) 之和[24]。利用有限差分法对薛定谔方程和泊松方程进行数值求解。然后将方程式(11) 离散在一个具有Nz节点的z方向网格上,并转化为三对角块形式的6Nz×6Nz特征值问题。本文中计算GaN/AlN量子阱使用的关键参数如表1所示。
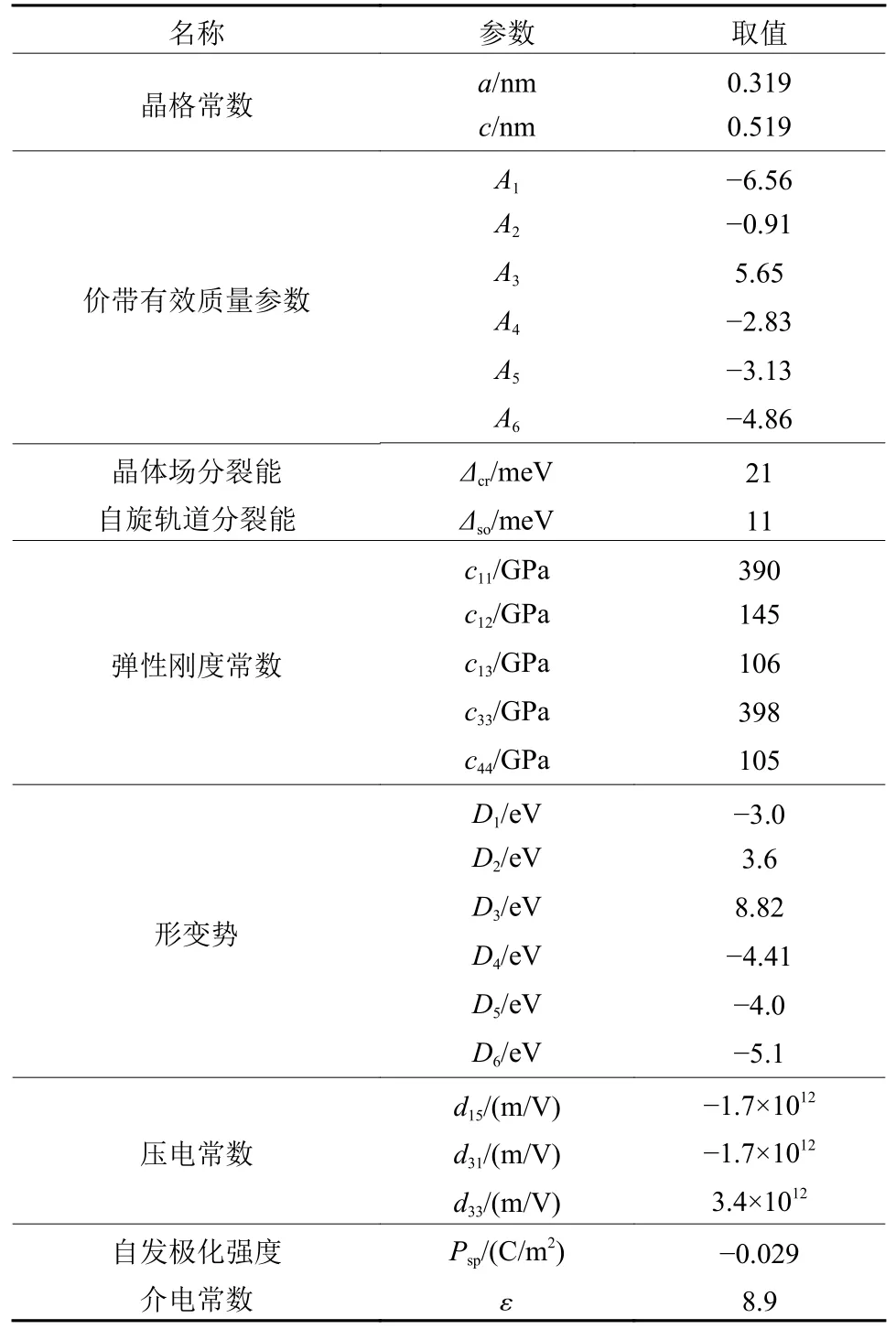
表1 计算中GaN的关键参数[25-27]Table 1 Key parameters of GaN in calculation[25-27]
2 结果与讨论
图4显示了应变张量分量、极化强度和极化场与倾角θ的关系。相应的极性和非极性晶面分别为θ=0°(沿c轴或[0001]方向生长)和θ=90°(沿[1 01¯0]方向生长)。考虑到纤锌矿GaN的六重对称性,只计算了θ=0°和θ=90°之间的角。在图4(a)中,通常应变的符号对于拉伸应力为正,对于压缩应力为负。观察到应变分量 ϵyy是常数,应变分量ϵxx和 ϵzz分别在θ=0°和θ=90°处出现最大值,且在大多数区域其符号相反。此外,(0001)和(1 01¯0) 晶面的分量ϵxz为零,这意味着极性晶面的应变是各向同性的。
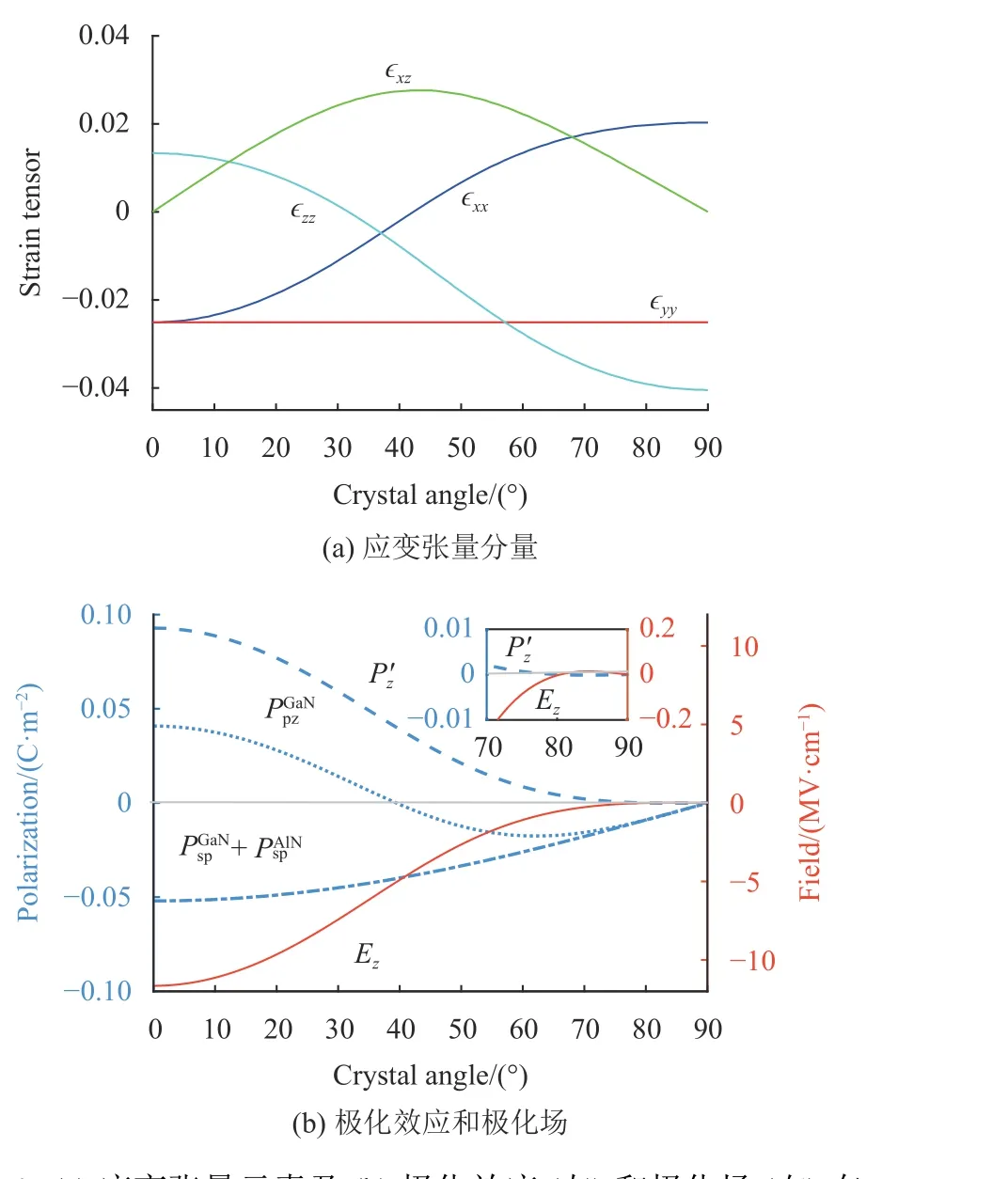
图4 (a) 应变张量元素及 (b) 极化效应 (左) 和极化场 (右) 在压缩应变GaN/AlN生长方向上与角θ的关系Fig.4 (a) Strain tensor elements and (b) polarization effect (the left) and polarization field (the right) with respect to the growth plane as a function of crystal angel θ for compressively strained GaN/AlN
根据式(8)至式(10),可以计算得到沿生长方向z′的极化强度和极化场。图4(b)显示了沿生长平面的应变诱导极化分量的结果,该结果取决于倾角θ,并对应于极化场,证明了GaN/AlN量子阱的总极化响应与晶体的对称性有关。由于在非极性(1 01¯0)晶面情况下,极化与生长方向垂直,不存在晶体对称性,Psp和Ppz为0,因此在该晶面上的极化场为0。在θ=0°处存在较大的压缩应变,使其P′z值出现最大值,因此在极性晶面纤锌矿GaN/AlN量子阱中产生强极化场。其中的插图显示了极化场在θ=81°附近为零,即Psp和Ppz在异质结中相互抵消。在θ=81°处和Ez′符号发生变化,其与应变条件有关。在极性晶面的情况下,Psp和Ppz产生的影响严格相加,在半极性异质结构中,加性效应则显著降低。
根据上述应变张量和极化效应对θ的依赖关系,计算了任意应力下GaN/AlN量子阱(0001)、(1 01¯2)和(1 01¯0)晶面的价带子带结构。本文研究了双轴应力和单轴应力下的应变效应。双轴应力不会破坏晶体对称性,只改变能级而不提升能带简并。然而,单轴应力产生的剪切应力对工艺制备来说很重要,因为它降低了晶体对称性,导致简并提升和能带翘曲,且单轴应力可以产生强烈的各向异性能面。由于沿z′方向的场约束对x′-y′平面内的能量色散没有显著影响,因此可以讨论应变下的平面内能量色散。
接下来,本文研究了双轴和单轴应力对价带子带二维等能图的影响。不同晶面的生长平面在文中用“平面内”表示,“平面外”是指在平面内之外。子带的二维等能图则是在平面内被描述。图5显示了在无应力下不同晶面GaN/AlN量子阱的最低能量子带的二维等能图。最低能量子带主导了顶部价带的性质,因为大多数空穴倾向于占据能量较低的价带。这里,k′x和k′y是(x′,y′,z′)坐标系中的平面波矢量,粗黑色箭头表示沟道方向(适用于本文所有二维等能图)。不同晶面的价带结构显示出有趣的特征:其形状强烈依赖于晶体生长方向,在(0001)晶面GaN/AlN量子阱的情况下,它是完全各向同性的。然而,半极性和非极性晶面在量子阱平面上表现出各向异性,而非极性晶面的各向异性更强。(1 01¯2 ) 和(1 01¯0)晶面的能量模式显示出二重对称性。具体而言,A、C区域(垂直于沟道方向)沿通道方向的曲率大于B、D区域(沟道方向)。因此,位于A、C上的空穴的有效质量比位于B、D上的小。在应力作用下,能量可以上下移动。因此,预计价带子带结构与空穴有效质量会受到单轴应力与晶体晶面的影响。
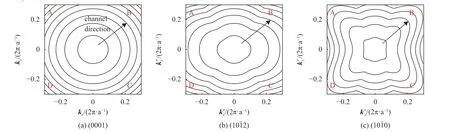
图5 无应力作用下不同晶面GaN/AlN量子阱的最低能量子带等能线Fig.5 Iso-energy contours of the lowest energy subband without stress with different crystal orientations for GaN/AlN quantum well
在晶体主坐标系中的平面内单轴应力由双轴压缩分量(sxx和syy)和剪切项(sxy)组成[28],如图6所示。为了方便比较,图7显示了双轴拉伸应力(sxx=syy=8 GPa)、无应力情况和双轴压缩应力(sxx=syy=-8 GPa)的不同晶面GaN/AlN量子阱的二维子带结构,分别由黑色虚线、灰色虚线和紫色实心等能线表示。可以看出,双轴应力几乎不影响(0001)晶面的价带结构。随着θ角的增大,等能线的变化更加明显。在图7(c)中,双轴拉伸应力使其最内层的等能线类似于圆形,而不是原来的六边形,其原因在于此时类轻空穴子带比类重空穴子带更接近Γ点。图8显示了在双轴拉伸和压缩下(0001)、(1 01¯2 ) 和(1 01¯0)晶面的最低子带能量。能量随应力上下移动,在拉应力下增加,在压应力下减少。这与已报道结果一致[29-30]。此外,它还揭示了双轴压缩降低了平面内区域的能量,将空穴从平面外区域移动到平面内区域。相反,双轴张力降低了平面外区域的能量。
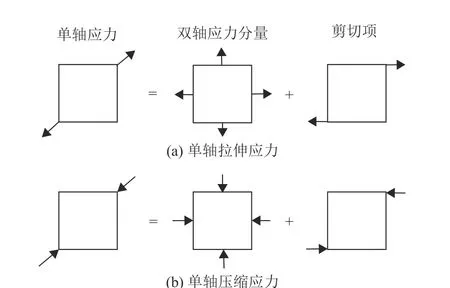
图6 单轴应力在传输平面上的等效效应Fig.6 The equivalent effect of uniaxial stress on the transport plane
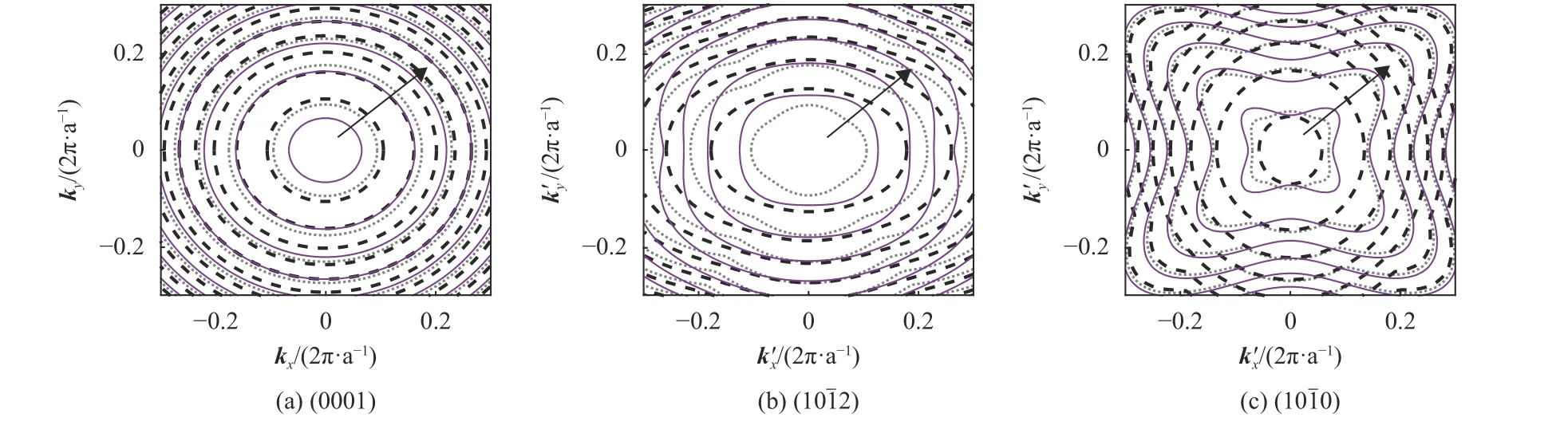
图7 8 GPa双轴应力作用于不同晶面GaN/AlN量子阱的最低能量子带间隔为100 meV的等能线Fig.7 Iso-energy contours separated by 100 meV for the lowest energy subband with the different crystal orientations under 8 GPa biaxial stress for GaN/AlN quantum well

图8 在不同应力配置下不同晶面GaN/AlN量子阱在 kx (或 k′x)方向的最低子带能量的比较Fig.8 Comparison of the lowest subband energies of different crystal orientations along kx (or k ′x) direction under different stress configurations for GaN/AlN quantum well
单轴应力与双轴应力不同,z轴方向对称性不再是C4v而是C2v,导致晶体对称性被严重破坏,影响了价带子带结构。在实验过程中可以采用四点弯曲试验设备施加单轴应力于输运面上[28]。图9显示了不同晶面GaN/AlN量子阱在沿沟道方向(即图中箭头方向)的8 GPa单轴拉伸应力(sxx=syy=sxy=4 GPa)和单轴压缩应力(sxx=syy=sxy=-4 GPa)作用下的二维等能图,其中明确显示了等能线最内部的形状近似于一个椭圆。图10显示了在不同应力配置下,(0001)、(1 01¯2)和(1 01¯0)晶面的结构沿沟道方向和垂直于沟道的最低能量子带能级。最低能级在沿A方向的单轴压缩应力下,导致A和C区域成为空穴有效质量减少的主要区域。在单轴拉伸应力下,空穴从轻空穴有效质量区域(A和C)重新填充到重空穴有效质量区域(B和D)。但对于单轴压缩应力,其显示出相反情况。单轴应力有助于打破子带结构对称性,改变载流子的分布并减少有效质量。根据上述结果,最有效的应力配置是沿沟道方向的单轴压缩应力,所得结果符合文献报道的结果[12,31-32]。
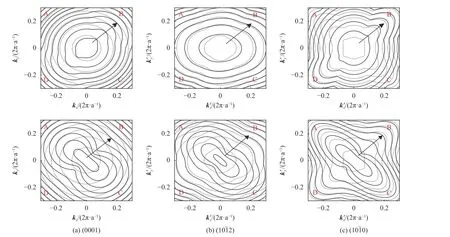
图9 在8 GPa单轴拉伸(上图)和压缩(下图)应力作用下不同晶面GaN/AlN量子阱中能量间隔为100 meV的最低能量子带的等能线Fig.9 Iso-energy contours separated by 100 meV for the lowest energy subband with the different crystal orientations under 8 GPa uniaxial tension (top) and compression (below) for GaN/AlN quantum well
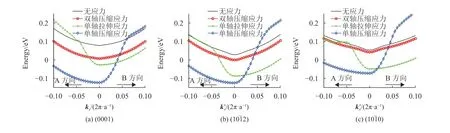
图10 不同应力配置下不同晶面GaN/AlN量子阱沿沟道方向(B方向)和垂直于沟道(A方向)最低子带能量的比较Fig.10 Comparison of the lowest subband energies of different crystal orientations along the channel direction (B direction) and perpendicular to the channel direction (A direction) under different stress configurations for GaN/AlN quantum well
为了量化有效质量的变化,本文基于子带结构的二维等能图对E-k关系求二阶导数,得到的结果列于表2中。无应力作用下(0001)晶面GaN/AlN量子阱的输运空穴有效质量比(1 01¯2) 和(1 01¯0)情况下的大得多。正如预期的那样,与其他应力配置相比,沿沟道方向的8 GPa单轴压缩应力可以显著降低不同晶面GaN/AlN量子阱的空穴有效质量,且比无应力情况下减少了约90%。

表2 不同晶面纤锌矿GaN/AlN量子阱在不同应力配置下沿沟道方向的空穴有效质量Table 2 Hole effective mass along the channel direction of wurtzite GaN/AlN quantum well with the different crystal orientations under different stress configurations
3 结论
本文利用一种综合模型研究了不同晶面纤锌矿GaN/AlN量子阱在双轴和单轴应力作用下的价子带结构。该模型基于k·p方法和自洽薛定谔-泊松方程,并且通过对(0001)晶面的k·p哈密顿矩阵进行旋转推导出半极性(1 01¯2 ) 及非极性(1 01¯0)晶面的矩阵。分析了双轴应力和单轴应力作用下的价带子带结构。此外,给出了GaN/AlN量子阱生长方向z′和c轴之间的倾角θ与应变和极化效应的关系。结果表明,在无应力作用下,半极性和非极性晶面的价带子带结构表现出各向异性,非极性晶面的子带等能线更加弯曲。双轴应力对极性晶面结构的有效质量的改善并不明显。然而单轴应力有利于打破晶体对称性,改变载流子的分布,降低空穴有效质量。其中,单轴压缩应力是降低空穴有效质量最有效的应力类型,且在不同晶面的结构中都减少了约90%。该研究结果为应变GaN材料及其器件的研究和设计提供理论指导和实验依据。

