关于含参量不等式恒成立问题的试题探究
——以2023年新高考I卷第19题为例
汤一鸣 马兆海 耿凤杰
(中国地质大学(北京)数理学院 100083)
1 引言
含参量不等式恒成立问题是不等式、函数、方程等知识的交叉,对于这类新高考的热点考题,学生在学习过程中难以形成固定的解题策略,遇到这一类问题时失分严重.不等式恒成立问题与函数最值联系紧密,要求学生将化归、分类讨论、函数与方程等数学思想融会贯通,学会一题多解.本文以2023年新高考Ⅰ卷第19题为例谈谈该问题的解题教学策略.
2 追本溯源,真题呈现
已知函数f(x)=a(ex+a)-x.
(1)讨论f(x)的单调性;
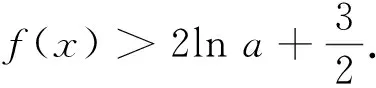
3 拨云见日,解法探究
(1)f′(x)=aex-1,当a≤0时,f′(x)<0在R上恒成立,f(x)在R上单调递减;当a>0时,令f′(x)=0,得x=-lna,在(-∞,-lna)上f′(x)<0,在(-lna,+∞)上f′(x)>0.综上所述,当a≤0时,f′(x)<0在R上恒成立,f(x)在R上单调递减;当a>0时,f(x)在(-∞,-lna)上单调递减,在(-lna,+∞)上单调递增.
第(2)题给出了3种解法:
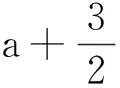
点评本题是一道典型的含参量不等式恒成立问题,但是它不具备进行参变量分离的条件,且其中给出的函数是非常规函数.注意到第一问求得f(x)的单调性,且不等式的右端不含自变量x,根据不等号的方向确定我们只需寻求f(x)的最小值,从而直接转化成求解函数f(x)的最小值问题.对于此解法,由于复习备考中对恒成立问题已有训练,因此学生容易想到利用导数思想求解函数相关问题,少数学生在问题转化过程中出现逻辑混乱,错误地去求了函数的最大值.
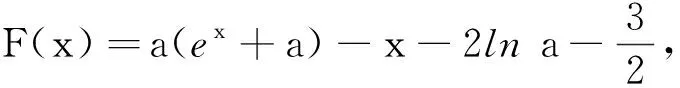
点评对于解决含参量不等式恒成立问题,移项构造函数不失为学生容易接受的方法之一,所以大部分学生能够考虑到将原问题转化为求解新构造函数的最值,使原问题迎刃而解.可是,运用这种方法的弊端在于,在中学数学知识范围内,新构造的函数不一定能顺利求得其最值,所以学生可以在尝试该方法的基础上判断是否可行.对于此解法,部分学生得到新构造函数的最小值后发现形式不够简洁,并不能一眼看出正负,从而产生错误的心理暗示,无法继续求解.
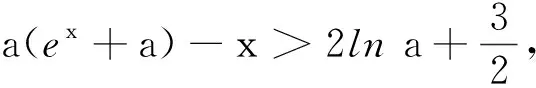
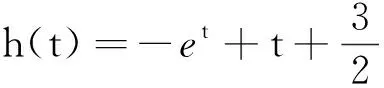
4 活学活用,变题训练
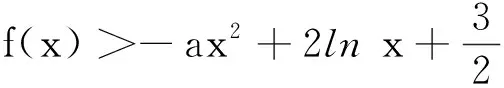
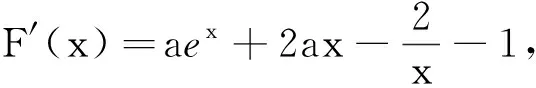
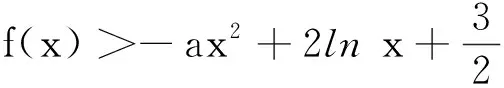
变题2已知函数f(x)=ex-a,证明:当a≤0时,f(x)≥e ln(ex+a).
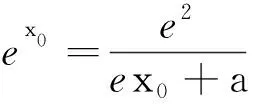
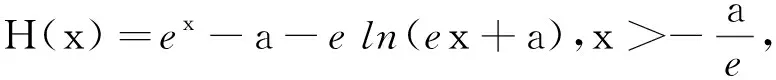
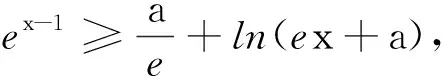
5 教学建议
(1)重视解题灵感与基本题型相结合
对学生而言,通过恒等变形构造函数及带有隐零点的函数最值问题常常成为解决问题的“拦路虎”.真题解法3和变题2中,利用恒等变形的基础是熟练运用指数与对数运算进行化简,带有隐零点的函数最值问题建立在用导数方法分析函数的最值之上.学生无法将这些基本题型迁移到待解决的问题上,解题思路就很难顺畅.解题灵感来源于对高中数学基本题型解题方法的积累,教学环节一方面应注重对基础知识的深度理解,培养学生的领悟力与独立分析能力,另一方面建议以教材为基础,以新高考试题为标杆,加强优质习题课建设,夯实基础,将各部分知识系统化处理与融合,激发学生的学习热情,推动由“双基”到能力的升华.
(2)重视数学思想的本质教学
数学思想是数学学科本质的集中体现,是数学最为显著的特征,是支撑全部数学大厦的脊梁,是数学知识发展的主线,是数学重要成就的提炼与反映[2].转化思想、分类讨论思想和函数与方程思想在含参量不等式恒成立问题中的地位尤为显著.学生总是将数学思想当作一种“方法”,形成做题的思维定式.比如在变题1中,学生容易陷入直接证明恒成立的“泥潭”,若换个角度思考,利用反证法,将恒成立作为条件,思路会柳暗花明.作为教师,应从数学思想角度切入教学,给予学生有价值的落脚点,充分发挥数学思想在育人层面上的抓手作用.因此,教学中应该摒弃一些逻辑思维跨度大、技巧性强的题目,避免给学生造成就题论题的困境,否则将不利于其深刻领悟其中蕴含的数学思想.教师在讲授含参量不等式恒成立问题时,可以详细解读典型例题,注重凸显不同例题中数学思想的本质区别,给学生时间去领会如何找到问题的突破口,以培养良好的数学思维品质.
(3)重视一题多解与一题多变
参变量分离法是学生解决含参量不等式恒成立问题的“法宝”.从真题角度上看,不是所有题目都能分离参变量,学生往往只知道方法本身而忽视了方法适用的条件.其实真题的解法多变,但考场上学生往往局限于一题一解,凭借自己的“经验”解决问题,一旦思路阻断就无法解题,因此课堂教学不是简单解决问题的过程,还要教师注重一题多解的教学.高考试题具有稳中求变的特点,要求教师经过变题解题教学,帮助学生梳理变题中不变的思路与破题点,挖掘变题的创新之处,培养学生全方位思考的品质.

