初中数学“链+”课堂教学资源的建设与思考
——以人教版“锐角三角函数”(第1课时)为例*
冯 娟
(江苏省如皋市实验初中 226500)
印冬建
(江苏省如皋市教师发展中心 226500)
教材是数学教学最重要的工具.在初中数学“链+”课堂[1]中,核心教学资源一般取自教材.但有时由于教材资源与学生认知水平、发展速度不能完全匹配,教师常会基于学生的发展需求,对教材资源进行优化调整与丰富完善,重构课时教学资源.“链+”是重构数学教学资源的一种有效策略,教师通过丰富教材资源优化教学过程,形成环环相扣的课时资源,推动学生数学核心素养发展,达成学科育人目标.本文结合人教版九年级下册“锐角三角函数”(第1课时)的教学资源建设谈谈笔者的思考,供大家参考.
1 教学分析
1.1 教材资源简述
教学资源见表1.

表1 教学资源
1.2 学情分析
在学习本节内容之前,学生已经学习了正比例函数、一次函数、二次函数、反比例函数,对函数的学习内容、方法、流程等都有了最基本的认识.但由于上述函数的学习均是在代数中展开的,而本单元要探索的正弦、余弦、正切等锐角三角函数均是基于图形展开的,其在探索过程、内容与方式上与前面的函数学习有明显差异.因此,如何将学生在前面函数中积累的“四基”巧妙地迁移到新的函数学习中来,并在形向数转化的过程中得到深度应用,将是本节课的一个难点.
此外,在本节课前学生已经较为系统地研究了直角三角形的两锐角关系、勾股定理、相似三角形等知识,在此基础上,自然地应进一步研究直角三角形的边角关系.这是为后续解直角三角形作铺垫,更是学习立体几何、解析几何以及物理中的力学的有力工具.
基于以上分析,我们将本节课的重点确定为直角三角形中边角关系的提出过程以及锐角正弦的定义,将“在概念形成之前,研究直角三角形中锐角的对边和斜边的比值和锐角的对应关系”确定为本节课的教学难点.当然,本节课除了让学生理解正弦的概念之外,还应让学生感受到学习三角函数知识的必要性、三角函数知识对科技发展的作用.
1.3 教学资源建设设想
基于学情和教材给定的教学资源,充分考虑学生发展的需求,我们拟定对教材资源进行扩充建设,在用好教材的基础上,从下面三个方面对教学资源进行整合与优化.
(1)增加教学资源的函数味
此前学生已学过一次函数、二次函数、反比例函数,锐角三角函数作为函数的一种,在教材中直到第2课时才在旁边注释中提及.教材中锐角三角函数仅作为一个比值给出,没有像研究其他函数那样,从定义、图象、性质等方面进行学习.高中数学教材教师用书中指出,学习三角函数时应注意以函数的一般概念为指导,借鉴其他函数的研究经验,引导学生自主构建三角函数的研究内容、过程和方法[2].从这个角度看,初中教材与高中教材联系甚少,常常会让学生感觉初高中学习的三角函数是两个不同的知识内容.为了打破这一现状,我们应增加教学资源的“函数味”,让学生体会到“直角三角形中锐角的度数与相关边的比值之间的单值对应关系”,加深学生对锐角三角函数的理解.
(2)增加教学资源的文化味
人类对三角函数的认知有着漫长的历史.三角学的原义为三角形测量,古希腊、印度、阿拉伯数学中三角函数的出现最初是由于天文观测的需要.我国古代最初虽没有出现三角函数概念,但是据《周髀算经》记载,与泰勒斯约为同时代的陈子已利用勾股定理测量太阳的高度,而后徐光启等人编写了《测量全义》,其中有平面三角和球面三角的论述,这些都是我国古代数学家对锐角三角函数研究的重要证据.现在,在天气预报、建筑设计、航海、测量、国防中都能找到三角函数的影子,而且诸如物理中的简谐振动、交流电中的电流、潮汐等,有许多周期现象都可以建立三角函数模型来解释.人教版教材中虽然也有关注到三角函数的发展史,但内容较少,学生不太能理解研究锐角三角函数的意义和必要性,我们可以增加一些有利于学生学习的文化素材.
(3)增加教学资源的探究味
学生的探究能力不应仅仅体现在根据课本问题完成学习活动,更应体现在对研究内容的确定、研究方法的选择,以及研究结束后对研究过程的反思及研究经验的积累上.从这个角度看,本节课的学习不能单纯地停留在对正弦概念的探究上,而应该从知识结构的完整性出发,引导学生分析、归纳出直角三角形边、角关系的所有研究内容,形成一个研究框架,并对已有的“四基”展开合情迁移,为后续的余弦、正切学习积累知识与经验.这就要求我们应基于教材给定的教学资源,进行资源探究性升级,一方面给教材资源增加探究味,让结论的得出过程稍微复杂一些,增加探究的环节和时间,让学生在深度参与中获得结论;另一方面,可增加引发学生深度思考的新素材,为学生提供认识正弦的不同视角,让学生在经历了画图、计算、观察、猜想、论证等活动后,得到正弦的定义及全章的知能网络.
2 “锐角三角函数”(第1课时)教学资源建设及简析
·活动1 创设情境,引入课题
教学资源建设 教材资源1,新增资源1~2
新增资源1 介绍意大利比萨斜塔的小视频.
新增资源2 问题:对于直角三角形,我们研究过哪些知识?(角与角的关系,三条边的关系)我们还应该研究什么?那么边与角的关系是怎样的呢?本章我们将共同来研究直角三角形中锐角与任意两边的比值的关系.任意两边之比有哪些呢?(整理之后,确定共有3种类型可研究)
教学设计依次投影教材资源1、新增资源1,在学生观影后引导学生将“求出1972年时比萨斜塔的倾斜角”转化为数学问题:已知直角三角形的两边长,求锐角的度数.渐进呈现新增资源2,根据学生作答,逐步板书,引导学生梳理未来探究内容(图5中虚线框中内容).

图5
设计意图以教材资源1和新增视频资源1激发学生的学习兴趣,引出课题,说明锐角三角函数的学习是解决实际问题的需要.通过新增资源2 “前链后引”[1],引导学生回顾直角三角形已学过的知识,使学生认识到本节课的学习也是使知识结构更完整的内部需要,逐步确定研究内容,勾勒出本章的研究框架,整体感知直角三角形的知识结构.
·活动2 特例探索,猜想结论
教学资源建设 教材资源2~3,新增资源3
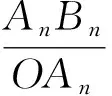

图6
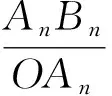
设计意图让学生经历从特殊到一般的探究过程,在已有结论的应用、特殊条件的推证和几何画板的展示中形成猜想:直角三角形中,当锐角A的度数一定时,∠A的对边与斜边的比值相等.
·活动3 抽象概念,巩固概念
教学资源建设 教材资源4,新增资源4~6
新增资源4 以单位圆为背景的一组练习题:
如图7,在平面直角坐标系中,以O为圆心、 1为半径作圆,交x轴正半轴于点A,点P(x,y)是圆上第一象限内的一个动点,设∠POA=α.

图7
(1)试表示出sinα.
(2)当α增大时,sinα如何变化?
(3)试分析sinα值的范围.

新增资源5 三角函数发展史与《托勒密与那张古老的“三角函数表”》史话材料.
基于史话材料的追问:随着人们对数学研究的不断深入,后来的三角函数表在此基础上不断完善.同学们,你们能不能利用提供给你们的正弦表,解决课堂一开始的问题呢?(屏幕呈现正弦表)求1972年比萨斜塔的倾斜角.
新增资源6 借助网络资源,介绍锐角三角函数在许多领域起到的作用,如科学研究、生产实践、军事活动等.
教学设计应用教材资源4,引导学生抽象新增资源1形成概念,结合学生探究的结果引出正弦定义.
设计意图练习题是利用高中三角函数的定义背景设置的,除了加深对正弦函数概念的认识,还增加了初中锐角三角函数的函数味,使学生初高中学习能更好地衔接.对学生进行数学文化熏陶的同时,解决古老的比萨斜塔倾斜角问题,感受三角函数的应用价值.
·活动4 知能梳理,总结引申
教学资源建设 新增资源7
新增资源7 问题:本节课我们学习了哪些知识?定义锐角正弦的过程、方式是什么?你认为今天这节课所学有什么作用?后续你还想自主研究哪些问题?
教学设计递进呈现新增资源7中几个小问题,引导学生在对话中总结全课收获,释疑解惑,形成基于课时的全域知识网络.
设计意图通过新增资源7,引导学生体会“锐角和边的比值间的函数关系”,对知识、方法进行梳理与总结,完善板书,形成单元知识结构.
3 三点启示
3.1 深入理解数学,为整体建构充实教学资源
数学教学要注意整体性,要注意将单个的数学知识与技能放到整体数学知能体系中展开教学.教师在进行数学教学前应首先站在学科视角去理解数学知能,从内涵到外延对所学知能进行全面剖析与解读,梳理知能的“来龙去脉”,从而确定知能教学的“边界”.在对知能有了较为全面理解的基础上,设计指向整体建构的教学资源,让知能在结构化的资源链中自然生长.因此,有时考虑到教材资源的不足,我们需要为梳理知能的“来龙”“去脉”而补充教学资源.本文课例是“锐角三角函数”的起始课,除了要学习正弦之外,还要整体建构单元的知识网络,也就是要让学生在锐角三角函数的知识结构中学习正弦.所以,我们基于教材资源补充“新增资源2”,唤醒学生掌握的直角三角形的角之间的关系、边之间的关系,逐步建构出的直角三角形的知识结构,并将本课时的边角关系探究合理纳入到这一结构中去,补齐知识网络缺口(图5);而最后补充的“新增资源7”,通过问题的渐进呈现引导学生回顾探索过程,梳理课时所学,猜想后续内容.这样的资源补充能促进学生对以正弦为起点的全章数学知能的整体建构,让学生在看到正弦这棵“树木”的同时,更看到了树木赖以生存的“森林”(全章知识网络).
3.2 全面解读教材,为全面认知完善教学资源
理解数学知能离不开教材解读,但“读教材就是读所教的教材”这样的理解显然是狭隘的.教材解读,一方面要解读教学内容所在的教材,理解知能本身,理解知能在本册教材中的地位,找寻出知能在本册教材中的关联内容;另一方面,要解读学段内的所有教材,甚至跨学段教材,充分厘清所学内容在学段乃至其在整个数学学习过程中的发展历程,彻底明晰课时知能生长的完整路径.全面的教材解读有助于教师从全面认知的教学出发增加能使新旧知识产生联系的教学资源,将知能横向、纵向链接在一起,帮助学生既认识知识本身,又发现知识内部之间存在着关联,形成更完善的知识结构.在文中这节课的教学中,不少学生感觉学习三角函数时较为困难,感觉初高中三角函数知识联系不大.为使初中三角函数的学习更好地链接到高中学习,适当增加初中锐角三角函数的“函数味”,设计中注重强调变化与对应,联系函数知识下定义.在活动3中,以补充的三个新增资源为纽带将两个学段的三角函数学习关联起来,既能巩固当堂课所学定义,也能链接到高中三角函数的研究背景,既能深化初中数学的学习、拓宽视野,又能为高中数学学习提供最近发展区.
3.3 合理优化进程,为素养提升增添教学资源
探究是学生获取数学知能的一条最重要的路径.近两版《义务教育数学课程标准》对学习活动的探究性均提出了较高的要求,对此,一线教师一直努力在教学中加以落实.但有时由于教材资源的探究性不足,如果仅按照教材给定的资源与流程教学,学生的素养难以得到充分发展.所以,对探究性资源不足的教学内容,可适当增加探究资源,并基于新增资源优化探究的过程,让学生的探究过程更加充分,增加知识获得过程的“含金量”,让学生在目标探究中形成积极向上的数学情感,形成良好的学习习惯以及正确的人生观、价值观.对于文中这节课而言,直角三角形的锐角与边的比值之间的函数对应关系是教学难点.为了让学生在体会这种对应关系的同时发展数学核心素养,教师新增几何画板资源(新增资源3),用几何画板动态演示,让学生从同类问题中发现结论,发展了几何直观、空间观念、逻辑推理等数学核心素养,获得了探索数学结论的一般方法,体会到特殊与一般的关系,初步形成学会辩证地看问题的能力.此外,借助史话材料《托勒密与那张古老的“三角函数表”》引导学生解决比萨斜塔倾斜角的问题,让学生学会用所学知识解决简单的实际问题,发展学生的几何直观、空间观念、逻辑推理、运算能力、应用意识等诸多核心素养.
教学资源是教学内容的载体,是教学目标得以实现的保障.在日常教学中,教师应多积累,多从学生的心理与认知特征考虑,放眼于长远的发展目标,适当补充教学资源.通过补充教学资源,使学生的认知过程更顺畅、知识结构更完整.通过补充教学资源,激发学生的数学学习兴趣,渗透数学历史与数学文化,促进其数学核心素养的提高.

