基于信号检测论的认知诊断评估：构建与应用*

郭 磊 秦海江

基于信号检测论的认知诊断评估：构建与应用*

郭 磊1,2秦海江1,3

(1西南大学心理学部;2中国基础教育质量监测协同创新中心西南大学分中心, 重庆 400715) (3贵阳市第三十七中学, 贵阳 550003)

作答选择题可被看作从噪音中提取信号的过程, 研究提出了一种基于信号检测论的认知诊断模型(SDT-CDM)。新模型的优势在于：(1)无需对选项进行属性层面的编码。(2)能获得传统诊断模型无法提供的题目区分度和难度参数。(3)可以直接表达每个选项之间的合理性差异, 对题目性能刻画更加细微全面。两个模拟研究结果表明：(1)EM算法可以实现对新模型的参数估计过程, 便捷有效。(2) SDT-CDM具备良好性能, 分类准确性和参数估计精度较高以外, 还能提供选项层面的估计信息, 用于题目质量诊断与修订。(3)属性数量、题目质量与样本量等因素会影响SDT-CDM的表现。(4)与称名诊断模型NRDM相比, SDT-CDM在所有实验条件下对被试的分类准确性更高。实证研究表明：SDT-CDM比NRDM具有更好的模型数据拟合结果, 其分类准确性和一致性更高, 尤其当属性考察次数较少时具有很强的稳定性, 难度和区分度参数与IRT模型估计结果的相关性也更高, 值得推广。

信号检测论, 认知诊断, 选择题, EM算法

1 引言

自Kelly (1916)第一次提出选择题(Multiple-Choice, MC)测验形式, 因其客观、有效、便捷等特点而广受欢迎, 直至当下仍是测验主流题型之一, 并广泛应用在TIMSS、PISA、NAEP和TOEFL等标准化测验。MC题型具有诸多优势：不受主观误差影响、提高测验信度、易于批阅且计分快速、满足内容平衡需求等(郭磊, 周文杰, 2021)。通常, MC作答数据被当作0-1计分形式(即答对或答错)处理, 但这样会造成干扰项信息的损失。为了充分挖掘干扰项的诊断信息, 提高个体知识状态的分类精度, 研究者提出了许多方法, 如MC-DINA模型(Multiple- Choice DINA; de la Torre, 2009)及其拓展的结构化MC-DINA模型(Ozaki, 2015), 包含干扰项信息的SICM模型(Scaling Individuals and Classifying Misconceptions Model; Bradshaw & Templin, 2014)和GDCM-MC模型(Generalized Diagnostic Classification Models for Multiple Choice Option-Based Scoring; DiBello et al., 2015), 以及基于选项层面的非参数认知诊断方法(郭磊, 周文杰, 2021; Wang et al., 2023)。这些方法的目标是在知识状态空间中对被试进行分类, 从而知晓其学科知识或认知属性的掌握情况, 这种评估方式也被称作认知诊断评估。但上述MC处理方法有个前提条件, 即要求对干扰项进行编码, 然后才能表征出区别于正确选项所表征的潜在类别。虽然前期的研究要求干扰项的编码需要是正确选项编码的子集、不同干扰项之间也要有包含关系(郭磊等, 2013), 但最近的研究已突破了该限制, 即干扰项的编码无需嵌套于正确选项编码中(Wang et al., 2023), 进一步推动了该领域研究。

实际上, MC测验也可以被视作一种信号检测任务, 被试需从一系列的噪音(所有选项)背景中选择出信号, 即做出正确反应。被试作答过程中存在两种可能性, 要么“会答/知道(Know)”, 要么“不会答/不知道(do not Know)”。从信号检测论(signal detection theory, SDT)的视角出发, 被试作答行为可包含两个阶段：①感知阶段：被试在理解题意后对每个选项产生不同程度的合理性1合理性可理解为基于个人知识、经验等因素认为该选项是正确的/合理的倾向性。(plausibility)判断, 可用合理性参数表达, 每个选项的合理性参数均服从一定分布。②决策阶段：被试在权衡每个选项的合理性后, 会做出选择最合理选项的决策。基于该理念, DeCarlo (2021)将SDT与项目反应理论(IRT)结合用于MC题目分析, 通过SDT模型可获得被试在选择各选项时的相对合理性参数、以及题目的区分度和难度参数信息。研究表明, SDT模型估计得到的难度参数与两参数、三参数项目反应模型基本一致, 但区分度参数仅与两参数模型相关较高, 与三参数模型相关低至0.04。此外, SDT还可以提供更丰富的信息, 如被试对每个选项尤其是干扰项的合理性倾向, 以及被试在每个选项上感知到的合理性差异(即选项差异)。因此, SDT对题目的解析更细微, 可以从选项层面知晓题目的整体情况, 其价值在于：①若某道题目偏简单, 为了增大该题目难度, 可以通过估计得到的选项合理性参数进行选项层面的针对性调整, 起到修订题目的作用。②诊断题目是否有问题。当被试“会答”该题目时, 选择干扰项的倾向性仍比选择正确选项的倾向性更大, 则预示着该题目的质量出现了问题。以上优势是两参数和三参数模型无法做到的。此外, SDT对MC题目的分析要比称名反应模型(Nominal Response Model, NRM; Bock, 1972)更加简洁易于解释。尽管NRM也可分析基于选项的数据, 但它引入了多个区分度参数, 使得参数估计和结果解释都变得复杂。若进一步想在NRM中表征猜测行为的话, 又需要引入更多的猜测参数, 这会导致模型参数增多并且难以估计(Thissen & Steinberg, 1997), 但SDT模型无需增加额外参数便可对猜测行为进行表征, 更加简约。并且根据DeCarlo (2021)的实证研究2600名被试参与的32道题目的学术评估测试(Scholastic Assessment Test, SAT), 每道题目有5个选项。表明, SDT模型比NRM有更好的模型拟合结果。

尽管在认知诊断评估中, Templin等(2008)将NRM拓展为称名反应诊断模型(Nominal Response Diagnostic Model, NRDM), 使之能够分析认知诊断的数据。随后, Ma和de la Torre (2016)提出了顺序G-DINA (sequential G-DINA)的模型框架, 将NRDM包含在内, 可实现对顺序(ordered)和称名数据的处理。但这些模型均是基于最初NRM思想的拓展, 也保留了NRM存在的问题, 如题目参数过多等问题：每道题目的每个选项都要估计截距项、主效应项及其交互作用项。因此, 基于SDT视角分析选项层面的诊断数据, 并探讨其适用价值具有重要意义。SDT用于认知诊断评估有以下优势：①无需对MC题目的选项进行编码, 节省大量人力物力。②在保证提供选项水平分析结果的前提下, 还可以使用更加精简的模型表达方式来达到比NRDM模型更好的解释意义, 参数更容易估计。③由于模型更加简洁, 模型和数据的拟合可能会进一步提升。④能够提供传统诊断模型无法提供的难度和区分度3传统诊断模型没有难度参数的具体表达, 而区分度是通过估计得到参数后计算才能得到。参数。

综上所述, 信号检测论视角的MC题型认知诊断评估将具备诸多优势, 因此本文拟探讨基于信号检测论的MC题型认知诊断评估方法与技术, 构建SDT-CDM模型并推导其参数估计方法, 并在模拟和实证测验中检验新模型的性能和有效性。本文结构如下：首先介绍SDT模型的逻辑背景, 其次阐述SDT诊断模型(记作SDT-CDM)的构建过程和参数估计方法, 之后通过模拟和实证研究探讨SDT- CDM的性能, 最后对结果进行讨论与展望。

2 SDT模型简介

被试在作答MC题目时, 首先会对每个选项产生不同程度的感知, 进而将这种感知转换成认为该选项是正确答案的合理性倾向。为了用模型表达出该加工过程, 可认为被试对每个选项的合理性倾向均服从一个概率分布, 如图1所示。

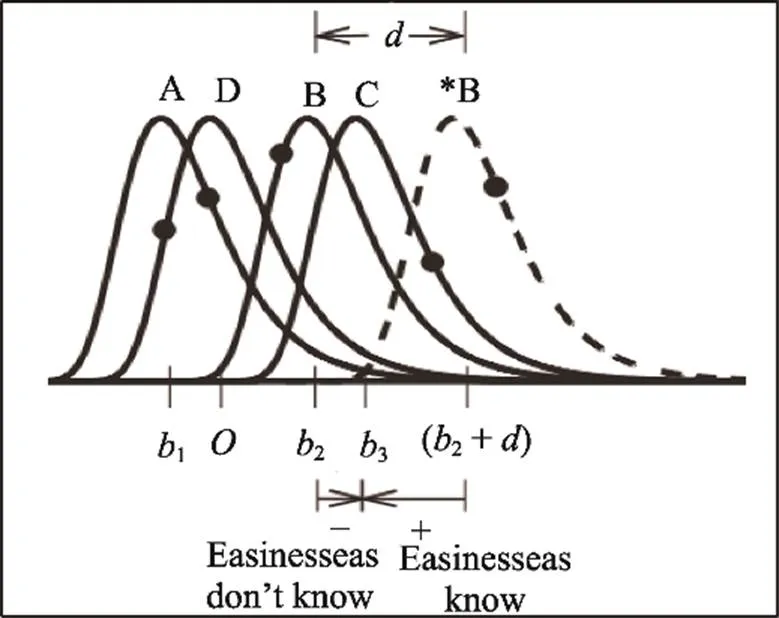
图1 SDT模型的反应示意图

(取自DeCarlo, 2021; P3, Figure 1)

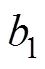
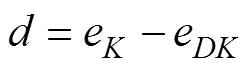
基于上述理论基础, SDT模型本质上是一个混合模型, 如公式(1)所示(详细推导请参见DeCarlo (2021))：

3 SDT-CDM的构建及参数估计

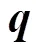
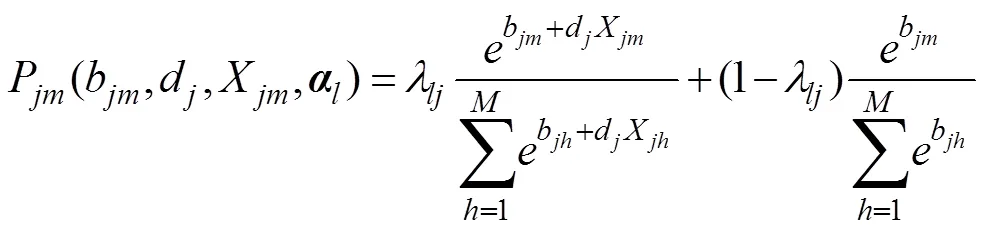
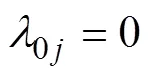
SDT-CDM的模型参数估计可用MMLE/EM算法实现, 算法推导过程及其标准误计算请参见网络版附录。

4 模拟研究1

4.1 研究目的

采用蒙特卡洛模拟方式探讨SDT-CDM在不同实验条件下对被试的分类准确性和参数估计精度。

4.2 实验设计

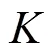
4.2.1 题目的模拟

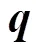
4.2.2 被试的模拟

被试的知识状态采取高阶和多元正态分布生成。其中, 高阶分布参考Ma和de la Torre (2016)的设置, 具体如下：

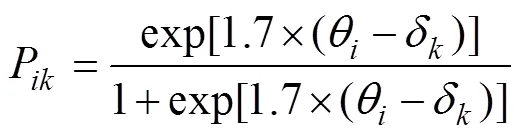
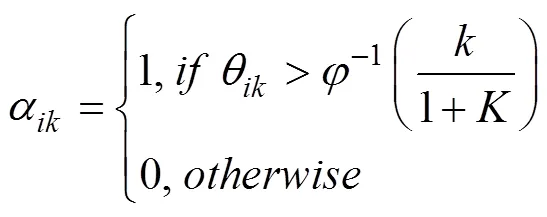
4.3 评价指标

参数估计精度的评价指标主要采用平均偏差Bias、均方误差根(root mean squared error, RMSE), 计算见公式(7)和公式(8)。

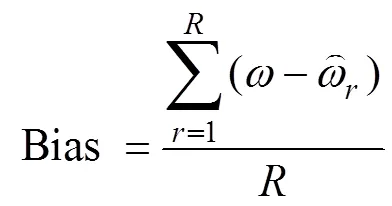
被试属性掌握情况的估计精度评价指标采用平均属性判准率(average attribute correct classificationrate, AACCR)和模式判准率(pattern correct classification rate, PCCR), 计算公式如下：

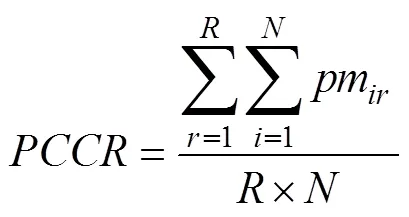
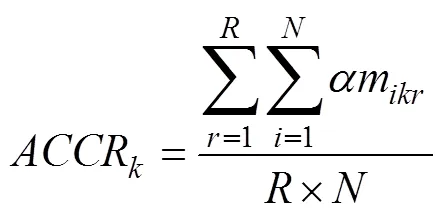
4.4 研究结果

图2和图3呈现了不同自变量水平下SDT- CDM的参数估计Bias和RMSE的总体结果。由于每道题目的合理性参数、属性主效应和属性交互效应的参数不止一个, 考虑呈现的简洁性和篇幅, 结果用均值表示。整体来看, 各参数的估计精度均较高, 如：合理性参数Bias范围为−0.003至0.007, 均值为0.002; RMSE范围为0.119至0.261, 均值为0.173。区分度参数Bias范围为−0.054至−0.001, 均值为−0.022; RMSE范围为0.145至0.385, 均值为0.253。易度参数eK的Bias范围为−0.014至0.075, 均值为0.027; RMSE范围为0.181至0.334, 均值为0.260。其余参数不再赘述。

不同自变量对参数估计精度的影响不同。首先, 属性分布为高阶分布的精度要稍优于多元正态分布的精度, 如高阶分布下的b、d、eDK、eK、δ-M和δ-I参数的Bias(RMSE)均值分别为0.002(0.160)、−0.022(0.234)、0.046(0.245)、0.025(0.248)、0.001(0.078)和−0.001(0.154), 多元正态分布下的对应参数的Bias(RMSE)均值分别为0.002(0.187)、−0.022(0.271)、0.051(0.267)、0.029(0.271)、0.008(0.126)和−0.009(0.236)。其次, 属性个数越多, 精度会略有下降, 如由= 3变为= 5时, 尽管所有参数的Bias均值由0.009变为0.010, 但RMSE的均值由0.189增大至0.224, 增幅为18.5%。然而, 题目数量对参数估计精度的影响较小。当= 20增加至40题时, 所有参数的Bias均值由0.008变为0.010, RMSE的均值由0.203变为0.210, 相差无几。再次, 题目质量对精度的影响较大, 当题目质量由高变低时, 所有参数的Bias均值由0.000变为0.019, RMSE的均值由0.192变为0.221, 增幅为15.1%。最后, 样本量的影响最大, 当人数由2000降低至1000时, 所有参数的Bias均值由0.007变为0.010, RMSE的均值由0.179变为0.234, 增幅高达30.7%。

图2 SDT-CDM参数估计的Bias结果

注：为所有合理性参数的均值,为区分度参数, eDK为被试不会作答时的易度参数, ek为被试会作答时的易度参数, δ-M为属性的主效应, δ-I为属性的交互效应。横坐标“3-20-H-1000表示”3属性-20题-高题目质量-1000人的实验条件。

图3 SDT-CDM参数估计的RMSE结果

图4呈现了SDT-CDM的AACCR和PCCR判准率结果。整体而言, 新模型能够较为准确的对被试进行分类, 其分类精度同样会受不同自变量的影响。在本文关注的5个因素中, 对分类精度影响最大的是题目质量。当题目质量较低时, AACCR的范围为0.902至0.988, 均值为0.951, PCCR的范围为0.609至0.964, 均值为0.816; 当题目质量提升后, AACCR的范围为0.973至1.000, 均值为0.990, PCCR的范围为0.876至0.999, 均值为0.957, 增幅为17.4%。其次是属性个数对精度的影响, 当= 3时, AACCR的范围为0.950至1.000, 均值为0.983, PCCR的范围为0.858至0.999, 均值为0.951; 当= 5时, AACCR的下降幅度为2.5%, 而PCCR的下降幅度为15.7%。第三位的影响因素为题目数量, 题量越多, 对被试获得的信息就越多, 因此对其分类精度也会提升。如= 20时, 平均的AACCR和PCCR分别为0.958和0.841, 当= 40时, 平均的AACCR和PCCR分别提升至0.984和0.932, 增幅分别为2.7%和10.8%。而其余两个变量：属性分布和样本量对分类精度的影响不大。如高阶分布时的平均AACCR和PCCR分别为0.969和0.882, 多元正态分布时的平均AACCR和PCCR分别为0.972和0.891; 人数为1000人时的平均AACCR和PCCR分别为0.970和0.883, 当人数增长至2000时, 平均AACCR和PCCR分别为0.972和0.890, 相差无几。

图4 SDT-CDM的PCCR和AACCR判准率结果

5 模拟研究2

5.1 研究目的

采用蒙特卡洛模拟方式主要比较SDT-CDM和NRDM在不同实验条件下的被试分类准确性。NRDM模型如下所示：

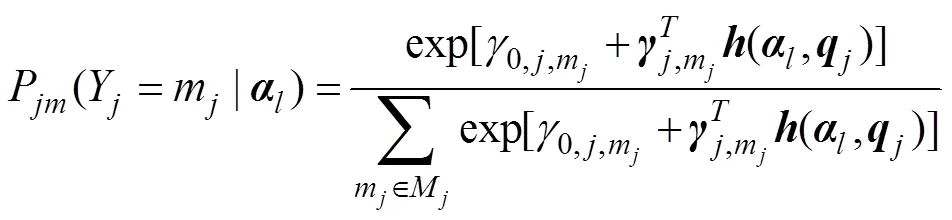
5.2 实验设计

5.3 研究结果

网络版附录图A1和网络版附录图A2直观地呈现了两个模型分别为真模型时在不同自变量水平下的PCCR和AACCR结果。不论真模型是哪个, SDT-CDM的表现均要优于NRDM。当SDT-CDM为真模型时, 属性分布对两个模型的分类精度影响均较小, 样本量仅对NRDM有中等程度影响(样本量增大, N-PCCR的均值提高了7.6%)。属性个数由3个增加至5个时, S-PCCR和N-PCCR的均值分别下降了12.9%和10.3%; 题目质量降低时, S-PCCR和N-PCCR的均值分别下降了14.3%和29.4%。值得注意的是, 题目数量对两个模型的影响趋势存在不同, 题目数量增大时, S-PCCR的均值提高了9.2%, 但N-PCCR的均值反而下降了18.2%。一个可能的原因是：题目数量越多, NRDM的题目参数数量将大幅度增长(由公式(12)可以看出), 因此需要更多的样本量才能保证题目参数的估计精度, 而当样本量不足时, 题目参数的估计精度会降低, 从而进一步降低了被试的分类精度。该影响也可以从最初提出NRDM的研究中得到佐证(Templin et al., 2008), 作者即使采用了缩减的补偿NRDM模型而非饱和的NRDM模型也需要高达5000人才能得到理想的参数估计精度。相对而言, SDT-CDM就表现的和大部分研究结果相近, 即题目数量越多, 分类精度越高, 这点也可以说明新模型对于处理诊断测验中的称名数据更为理想。同时, 这5即使是缩减的补偿NRDM模型也需要高达5000人才能得到理想的参数估计精度。也解释了为何NRDM作为真模型的表现仍不如SDT-CDM。当NRDM为真模型时, 尽管自变量对分类精度的影响趋势与真模型为SDT-CDM时类似, 但此时SDT-CDM与NRDM的表现差异要更小, 如题目质量降低时, S-PCCR和N-PCCR的均值分别下降了6.2%和14.8%, 这说明SDT-CDM比起NRDM具有更强的稳定性。

网络版附录表A1进一步呈现了不同自变量对两个模型差异的影响。不论真模型是哪个, 题目数量对于两者的影响均是最大的, 当= 20时, 两者表现相差无几; 但当= 40时, SDT-CDM比NRDM的PCCR均值在不同真模型条件下分别高出了42.29%和21.04%, 说明NRDM不太适合分析题目数量较多的测验, 若要分析则需要增加较多样本量, 而SDT-CDM在一定的样本量基础上就可以分析较多题量的测验情景。影响其次的是题目质量, 尤其当题目质量较低时, SDT-CDM比NRDM的PCCR均值在不同真模型条件下分别高出了36.06%和16.52%, 说明SDT-CDM可以有效缓冲题目质量较低产生的负面影响。接下来是样本量, 当样本量较小时, SDT-CDM比NRDM的PCCR均值在不同真模型条件下分别高出了24.72%和14.93%, 说明SDT-CDM比起NRDM来说更适合处理小样本。而其余变量均有不同程度的影响, 不再赘述。

通过上述结果综合来看, SDT-CDM从各方面都要优于NRDM, 通过详尽的模型比较研究, 进一步证明了新模型的优势：当实验条件变化时, SDT- CDM比NRDM更能维持住相对好的模型表现, 因此可以认为SDT-CDM比NRDM的适用场景更广, 表现更稳定。

6 实证研究

实证数据取自Ma和de la Torre (2020)使用过的TIMSS 2011数据, 该数据共包含23道数学测验题目, 本研究选择其中的14道选择题进行分析。数据中包含748名来自美国被试的作答数据, 数据中的缺失值采用随机的错误答案进行替换。Q矩阵属性个数为6个, 分别为：A1)整数; A2)分数、小数和比例; A3)表达式、方程式和函数; A4)线条、角度和形状; A5)位置和移动; A6)数据组织、表示和解释识别明确信息, 如表1所示。诊断结果的信效度指标采用Wang等(2015)提出的属性与模式分类一致性指标(Attribute-Level and Pattern-Level ClassificationConsistency), 以及属性与模式分类准确性(Attribute- Level and Pattern-Level Classification Accuracy), 它们可以分别从属性层面与模式层面综合判断诊断结果的信效度, 均是取值越高则表明信效度越好。为了展现SDT-CDM的实际表现, 在分析实证数据时加入了NRDM6使用R软件中的GDINA程序包进行参数估计。进行对比。

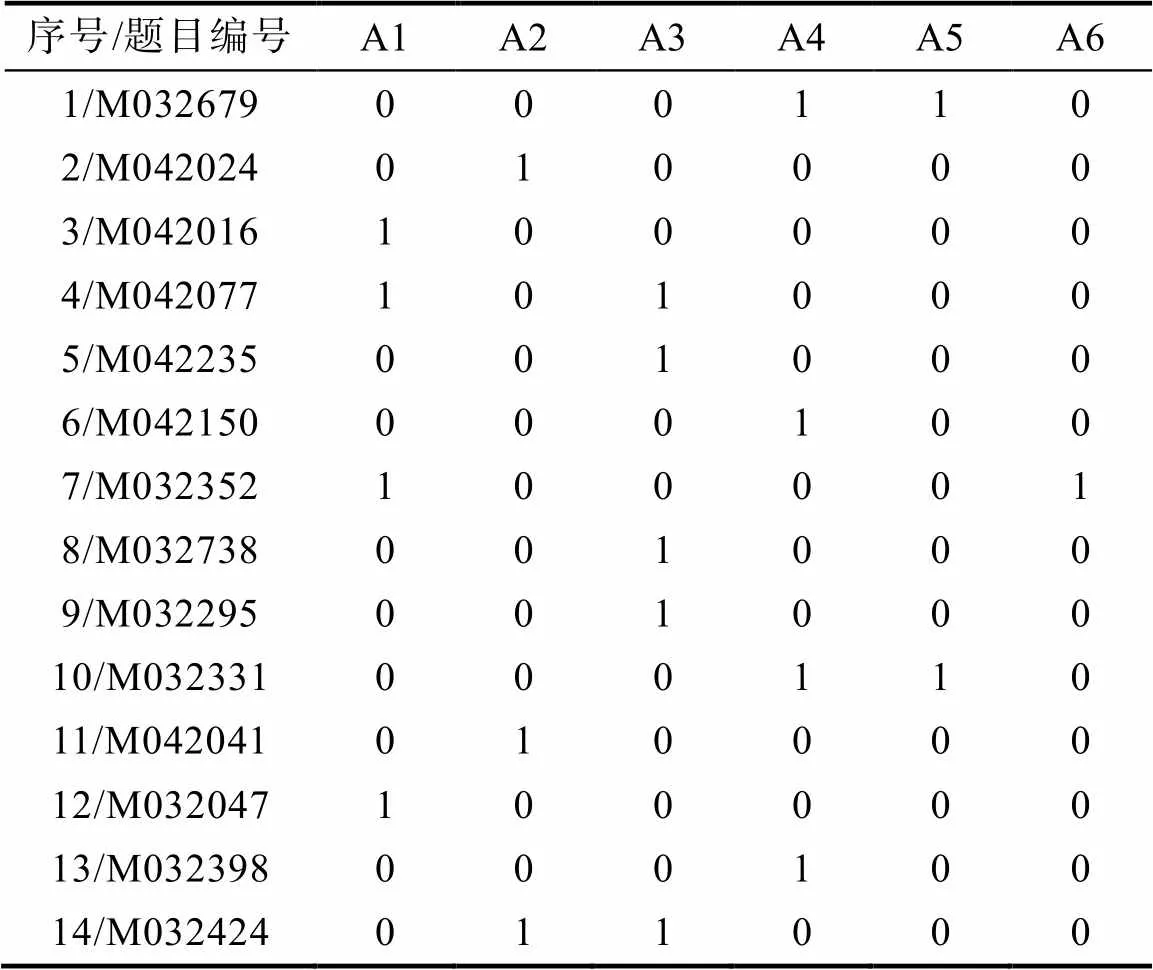
表1 TIMSS 2011数学测验(选择题)的Q矩阵

表2呈现了SDT-CDM与NRDM的模型−数据的相对拟合指标：负2倍对数似然值(−2 Log likelihood)、AIC (Akaike information criterion)与BIC (Bayesian information criterion), 三者均是取值越小越好。结果表明, SDT-CDM在3个拟合指标上的结果都要优于NRDM, 如粗体结果所示, 并且模型自由估计的参数数量为71个, 而NRDM需要估计87个参数, 更加复杂。

表2 模型数据相对拟合指标

网络版附录表A2和表A3分别呈现了SDT- CDM和NRDM的模型参数估计结果。由网络版附录表A2可以看出, 14道题目的区分度均为正值, 这表明“会答”题目的被试和“不会答”题目的被试能够被正常区分。理论上,越大则表明题目质量越好, 但根据DeCarlo (2021)实证数据参数估计结果的经验, 当过大时可能导致标准误的增大, 例如DeCarlo研究中在6以上的3道题, 其值的标准误均在8以上, 表明参数估计不稳定。相比之下, 本研究仅有第7题的值大于6, 其标准误为4.044远小于8, 整体来说, 估计结果较为理想。

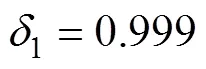
表3呈现了属性与模式的分类准确性和分类一致性指标(Wang et al., 2015)结果。在分类准确性上, SDT-CDM除A1属性低于NRDM之外, 其余属性的分类准确性和模式分类准确性均要高于NRDM, 尤其是模式分类准确性提升了39.13%, A6的属性分类准确性提升了23.77%; 在分类一致性上, SDT-CDM除A1属性低于NRDM之外, 模式和其余属性的分类一致性均要高于NRDM, 尤其是A6的属性分类一致性提升了28.63%。由表2的Q矩阵可知, A6仅被考察了1次, 相对其他属性被考察的次数偏少, 此时对NRDM的影响更大, 而SDT-CDM能够在有限考察次数内保持较高的分类准确性和一致性, 更加稳健。以上结果表明新模型可以得到比旧模型更佳的信效度结果。

表3 属性与模式水平的分类准确性和一致性

注：提升率 = (SDT-CDM − NRDM)/ NRDM

SDT-CDM从可能的64种知识状态中识别出748名被试各自所属的知识状态。图5呈现了被试数量最多的前10类知识状态, 总占比为79.3%。进一步计算SDT-CDM和NRDM估计得到的属性掌握程度与总分间的相关(郭磊, 周文杰, 2021), 相关高表明总分越高的被试其掌握属性的程度越好, 符合现实情况。其中, SDT-CDM为0.87 (< 0.001), NRDM为0.76 (< 0.001), 表明新模型的表现要优于NRDM。

图5 各类知识状态的被试占总体的比例(前十类)

6 讨论与研究结论

6.1 讨论与展望

MC作答过程可以看作是信号检测的过程, 意味着被试对每个选项都有一个合理性感知, 并且总会选择感知到合理性最强的选项。本研究将SDT模型整合进CDM中, 得到一些主要发现：首先, SDT-CDM无需对MC题目的选项进行编码, 而是为每个选项赋予了一个合理性参数, 用来刻画选项之间的差异, 并且通过这些合理性参数的组合可以计算得到传统诊断模型无法提供的难度和区分度参数, 这些信息可用于题目质量诊断及修订。通过研究表明, SDT-CDM的这些优势都是存在的, 其模型构建是成功的。其次, 通过两个模拟研究, 在5个因素上全面地检验了新模型的性能, 结果发现：(1)题目质量和样本量对SDT-CDM的参数估计精度影响较大, 而属性分布、属性个数和题目数量的影响较小。(2)题目质量、属性个数和题目数量对被试判准率的影响较大, 而属性分布和样本量对判准率的影响不大。(3)通过模型比较研究后发现, 不论真模型是哪个, SDT-CDM的被试判准率均要优于NRDM, 导致该现象的原因是由于NRDM需要很大样本量才能估计准确导致, 这也恰恰证明了SDT-CDM的现实适用性和稳健性。最后, 通过TIMSS 2011的实证数据分析发现, 不论是模型数据拟合, 分类精确性和一致性, 还是与IRT的难度和区分度的相关, 均是SDT-CDM表现更优。此外, 由表4所得结果可用于判断题目/选项的质量和合理性, 为完善和提升题目质量提供的针对性指标, 这也是NRDM所不能实现的功能。本研究值得探讨的问题还有以下几点。

6.1.1 干扰项信息的利用

6.1.2 EM算法的改进及标准误的计算

本研究推导了SDT-CDM的EM算法, 但EM算法存在多样的变式(Chalmers, 2012), 例如标准的EM算法(the standard EM algorithm with fixed quadrature)、蒙特卡洛EM估计(Monte Carlo EM estimation)、随机EM算法(the stochastic EM)、MH-RM算法(Metropolis-Hastings Robbins-Monro algorithm)、最小化卡方的EM (朱玮等, 2006)等, 这些算法大部分已应用于IRT研究领域, 且可以通过软件包实现。然而, 目前在CDM中的EM算法比较单一, 从de la Torre (2009)提出DINA模型的边际极大似然的EM算法(MMLE/EM)后, MMLE/EM便一直是主要的估计算法, 包括本文也是使用这一框架拓展。尽管MMLE/EM算法简单高效, 但探索精度更高、收敛更快、或具有其他独特优势的新算法很有必要。未来可以考虑将IRT里较为成熟的算法引入新模型中。

此外, CDM中参数估计的标准误采用信息矩阵的逆求解, 但目前已有多种信息矩阵(刘彦楼, 2022), 例如经验交叉相乘信息矩阵法(Empirical Cross-product Information Matrix, XPD)、观察信息矩阵法(Observed Information Matrix, Obs)和三明治信息矩阵法(Sandwich-type Information Matrix, Sw)等。本文使用的是XPD矩阵, 未来可探索使用不同信息矩阵对SDT-CDM参数标准误估计的影响。

6.1.3 与过程性数据相结合

随着计算机技术的发展, 记录被试的作答过程性数据变得方便快捷, 许多研究者开始挖掘这些过程性数据所提供的信息是如何帮助提升被试知识状态的诊断精度, 以及反映出不同的作答风格或策略。如, 和反应时数据结合的诊断(郑天鹏等, 2023), 和眼动数据结合的诊断(詹沛达, 2022), 以及和动作序列结合的诊断(Zhan & Qiao, 2022)。这些研究均将过程性数据融入CDM中, 并证明了融入辅助信息的可行性和有效性, 为多模态数据分析提供了方法。尽管挖掘过程性数据中蕴含的信息已被研究者接受, 但尚未就如何能更好地分析它们达成共识(He et al., 2021), 同时, 用于分析过程性数据本身的模型或方法也具有多样性, 如处理计数数据的模型包括泊松模型(poisson model)、负二项式模型(negative binomial model)、零膨胀模型(zero-inflated model)、跨栏模型(Hurdle model)等。再如, 动作序列的提取方法也有很多, 如潜在空间模型(latent space model, Chen et al., 2022), 基于递归神经网的序列到序列自动编码器(recurrent neural network-based sequence-to-sequence autoencoders, Tang et al., 2021), 及多维尺度法(multidimensional scaling, Tang et al., 2020)等, 不同的特征提取方法也会影响诊断分类的效果。未来可以探讨不同的过程性数据模型和不同的特征提取方法与SDT-CDM结合的实际效果。

6.1.4 与追踪诊断相结合

纵向追踪诊断研究也是CDA领域近年来的一个研究热点, 通过对学习过程的追踪, 不仅能进一步刻画学生的学习轨迹, 更能有效发挥CDA的诊断功能, 帮助教师等实施针对性补救教学, 最终促进学生发展。目前纵向CDM包括基于潜在转移分析的纵向CDM (Wang et al., 2018; Zhang & Chang, 2020)和基于高阶潜在结构的纵向CDM两大类(Lee, 2017; Zhan et al., 2019), 未来可以考虑将SDT模型融入纵向CDM中, 不仅实现对被试知识状态的追踪, 还能随时间点观察题目质量的改变。

本研究尚存一些不足之处, 例如本研究只将SDT-CDM与NRDM进行比较, 虽然这是由于能够处理选项层面数据且不需要选项层面编码的CDM较少导致, 但正是缺乏更多的对比目标导致难以对SDT-CDM模型进行更深一步的探索研究。本文使用的XPD信息矩阵属于解析法信息矩阵, 而解析法信息矩阵在计算CDM模型参数的标准误时可能会遇到矩阵非正定、以及方差协方差矩阵对角线元素可能小于0等问题, 导致无法求解出标准误。因此计算标准误更好的方法是采用刘彦楼(2022)提出的“并行自助法”, 以类似于蒙特卡洛模拟的方式进行计算, 可以不受解析法信息矩阵的限制, 但本研究并未探索该方法在SDT-CDM模型中的有效性。此外, 本文使用的MMLE/EM算法尽管高效, 但EM算法可能会陷入局部最优解, Zeng等(2023)提出了Tensor-EM算法, 较好地改善了局部最优解的困境, 对于复杂模型而言是很好的参数估计方法。

6.2 研究结论

本研究提出了基于信号检测论的认知诊断模型SDT-CDM, 基于模拟和实证研究结果, 得出如下结论：

(1) SDT-CDM可以通过EM算法实现其参数估计。除能提供传统诊断模型不能提供的题目难度和区分度参数外, 还能估计得到每个选项的合理性参数, 通过这些题目参数信息可以对题目进行修订以提高其质量。

(2)模拟研究结果表明, SDT-CDM参数估计精度较好, 不同自变量对题目参数和被试分类精度存在影响。其中, 对分类精度影响重要性排序为：题目质量、属性个数和题目数量, 而属性分布和样本量对精度的影响较小。

(3)实证研究结果表明, SDT-CDM比NRDM有更好的模型数据拟合结果, 更高的模式/属性分类准确性和一致性(尤其当某个属性被考察次数较少时, SDT-CDM展现出了极高的稳定性), 被试属性总体掌握程度与其总分的相关结果也更高, 且无需对干扰项进行编码。此外, 可以根据两个易度参数(eDK和eK)和区分度参数对题目质量进行诊断及针对性修订。

Bock, R. D. (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories.(1, Pt. 1), 29–51.

Bradshaw, L., & Templin, J. (2014). Combining item response theory and diagnostic classification models: A psychometric model for scaling ability and diagnosing misconceptions.(3), 403–425.

Chalmers, R, P. (2012). mirt: A multidimensional item response theory package for the R environment.(6), 1–29.

Chen, Y., Zhang, J., Yang, Y., & Lee, Y.-S. (2022). Latent space model for process data.(4), 517–535.

Chiu, C.-Y. (2013). Statistical refinement of the Q-matrix in cognitive diagnosis.(8), 598–618.

Cohen, J. (1988).(2nded.). New York, NY: Erlbaum.

DiBello, L. V., Henson, R. A., & Stout, W. F. (2015). A family of generalized diagnostic classification models for multiple choice option-based scoring.(1), 62–79.

DeCarlo, L, T. (2021). A signal detection model for multiple- choice exams.(6), 423–440.

de la Torre, J. (2009). DINA model and parameter estimation: A didactic.(1), 115–130.

de la Torre, J. (2011). The generalized DINA model framework.(2), 179–199.

Fang, G., Liu, J., & Ying, Z. (2019). On the identifiability of diagnostic classification models., 19–40.

Guo, L., Yuan, C. Y., & Bian, Y. F. (2013). Discussing the development tendency of cognitive diagnosis from the perspective of new models.(12), 2256–2264.

[郭磊, 苑春永, 边玉芳. (2013). 从新模型视角探讨认知诊断的发展趋势.(12), 2256–2264.]

Guo, L., Zheng C., Bian Y., Song N., & Xia L. (2016). New item selection methods in cognitive diagnostic computerized adaptive testing: Combining item discrimination indices.(7), 903–914.

[郭磊, 郑蝉金, 边玉芳, 宋乃庆, 夏凌翔. (2016). 认知诊断计算机化自适应测验中新的选题策略：结合项目区分度指标.(7), 903–914.]

Guo, L., & Zhou, W. J. (2021). Nonparametric methods for cognitive diagnosis to multiple-choice test items.(9), 1032–1043.

[郭磊, 周文杰. (2021). 基于选项层面的认知诊断非参数方法.(9), 1032–1043.]

He, Q., Borgonovi, F., & Paccagnella, M. (2021). Leveraging process data to assess adults’ problem-solving skills: Using sequence mining to identify behavioral patterns across digital tasks.: 104170.

Kelly, F. J. (1916). The kansas silent reading tests.(2), 63–80.

Lee, S. Y. (2017).(Unpublished doctorial dissertation). University of California, Berkeley.

Liu, Y. (2022). Standard errors and confidence intervals for cognitive diagnostic models: Parallel bootstrap methods.(6), 703–724.

[刘彦楼. (2022). 认知诊断模型的标准误与置信区间估计：并行自助法.(6), 703–724.]

Ma, W., & de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses.(3), 253– 275.

Ma, W., & de la Torre, J. (2020). An empirical Q-matrix validation method for the sequential generalized DINA model.(1), 142–163.

Ozaki, K. (2015). DINA models for multiple-choice items with few parameters: Considering incorrect answers.(6), 431–447.

Tang, X., Wang, Z., He, Q., Liu, J., & Ying, Z. (2020). Latent feature extraction for process data via multidimensional scaling., 378–397.

Tang, X., Wang, Z., Liu, J., & Ying, Z. (2021). An exploratory analysis of the latent structure of process data via action sequence autoencoder.(1), 1–33.

Templin, J., Henson, R., Rupp, A., Jang, E., & Ahmed, M. (2008).. Annual Meeting of the National Council on Measurement in Education, New Brunswick, New Jersey.

Thissen, D., & Steinberg, L. (1997). A response model for multiple-choice items. In W. J. van der Linden & R. K. Hambleton (Eds.),(pp. 51–65). Springer.

Wang, S., Yang, Y., Culpepper, S. A., & Douglas, J. A. (2018). Tracking skill acquisition with cognitive diagnosis models: A higher-order, hidden markov model with covariates.(1), 57–87.

Wang, W., Song, L., Chen, P., Meng, Y., & Ding, S. (2015). Attribute-level and pattern-level classification consistency and accuracy indices for cognitive diagnostic assessment., 457–476.

Wang, Y., Chiu, C.-Y., & Kohn, H. F. (2023). Nonparametric classification method for multiple-choice items in cognitive diagnosis.(2), 189–219.

Xu, G. (2017). Identifiability of restricted latent class models with binary responses.(2), 675–707.

Xu, X., Chang, H., & Douglas, J. (2003).. Paper presented at the annual meeting of National Council on Measurement in Education, Montreal, Quebec, Canada.

Zeng, Z., Gu, Y., & Xu, G. (2023). A tensor-EM method for large-scale latent class analysis with binary responses., 580–612.

Zhan, P. D. (2022). Joint-cross-loading multimodal cognitive diagnostic modeling incorporating visual fixation counts.(11), 1416–1432.

[詹沛达. (2022). 引入眼动注视点的联合-交叉负载多模态认知诊断建模.(11), 1416–1432.]

Zhan, P. D., Jiao, H., Liao D. D., & Li, F. M. (2019). A longitudinal higher-order diagnostic classification model.(3), 251–281.

Zhan, P. D., & Qiao, X. (2022). Diagnostic classification analysis of problem-solving competence using process data: An item expansion method.(4), 1529– 547.

Zhang, H. C., & Xu, J. P. (2015).(4thed.). Beijing Normal University Press.

[张厚粲, 徐建平. (2015).(第4版). 北京师范大学出版社.]

Zhang, S. S., & Chang, H. H. (2020). A multilevel logistic hidden markov model for learning under cognitive diagnosis., 408–421.

Zheng, T. P., Zhou, W. J., & Guo, L. (2023). Cognitive diagnosis modelling based on response times.(2), 478–490.

[郑天鹏, 周文杰, 郭磊. (2023). 基于题目作答时间信息的认知诊断模型.(2), 478–490.]

Zhu W., Ding S., & Chen X. (2006). Minimum chi-square/EM estimation under IRT.(3), 453–460.

[朱玮, 丁树良, 陈小攀. (2006). IRT中最小化χ2/EM参数估计方法.(3), 453–460.]

Cognitive diagnostic assessment based on signal detection theory: Modeling and application

GUO Lei1,2, QIN Haijiang1,3

(1Faculty of Psychology, Southwest University;2Southwest University Branch, Collaborative Innovation Center of Assessment toward Basic Education Quality, Chongqing 400715, China) (3Guiyang No.37 Middle School, Guiyang 550003, China)

Cognitive diagnostic assessment (CDA) is aimed at diagnose which skills or attributes examinees have or do not have as the name expressed. This technique provides more useful feedback to examinees than a simple overall score got from classical test theory or item response theory. In CDA, multiple-choice (MC) is one of popular item types, which have the superiority on high test reliability, being easy to review, and scoring quickly and objectively. Traditionally, several cognitive diagnostic models (CDMs) have been developed to analyze the MC data by including the potential diagnostic information contained in the distractors.

However, the response to MC items can be viewed as the process of extracting signals (correct options) from noises (distractors). Examinees are supposed to have perceptions of the plausibility of each options, and they make the decision based on the most plausible option. Meanwhile, there are two different states when examinee response to items: knows or does not know each item. Thus, the signal detection theory can be integrated into CDM to deal with MC data in CDA. The cognitive diagnostic model based on signal detection theory (SDT-CDM) is proposed in this paper and has several advantages over traditional CDMs. Firstly, it does not require the coding of-vector for each option. Secondly, it provides discrimination and difficulty parameters that traditional CDMs cannot provide. Thirdly, it can directly express the relative differences between each options by plausibility parameters, providing a more comprehensive characterization of item quality.

The results of two simulation studies showed that (1) the marginal maximum likelihood estimation approach via Expectation Maximization (MMLE/EM) algorithm could effectively estimate the model parameters of the SDT-CDM. (2) the SDT-CDM had high classification accuracy and parameter estimation precision, and could provide option-level information for item quality diagnosis. (3) independent variables such as the number of attributes, item quality, and sample size affected the performance of the SDT-CDM, but the overall results were promising. (4) compared with the nominal response diagnostic model (NRDM), the SDT-CDM was more accurate in classifying examinees under all data conditions.

Further, an empirical study on the TIMSS 2011 mathematics assessment were conducted using both the SDT-CDM and the NRDM to inspect the ecological validity for the new model. The results showed that the SDT-CDM had better fitting and a smaller number of model parameters than the NRDM. The difficulty parameters of the SDT-CDM were significantly correlated with those of the two- (three-) parameter logical models. And the same was true of the discrimination parameters for the SDT-CDM. However, the correlation between the discrimination parameters of the NRDM and those of the two- (three-) parameter logical models was low and not significant. Besides, the classification accuracy and classification consistency of the SDT-CDM were higher than those of the NRDM. All the results indicated that the SDT-CDM was worth promoting.

signal detection theory, cognitive diagnostic assessment, multiple-choice items, expectation maximization algorithmtext

B841

2023-04-21

* 国家自然科学基金青年项目(31900793); 中央高校基本科研业务费专项资金(SWU2109222); 西南大学2035先导计划项目(SWUPilotPlan006)。

郭磊, E-mail: happygl1229@swu.edu.cn