任务相关性对数量感序列依赖效应的影响*

刘雨杰 刘晨淼 周丽琴 周 可

任务相关性对数量感序列依赖效应的影响*

刘雨杰1,2刘晨淼3周丽琴3周 可3

(1中国科学院生物物理研究所, 脑与认知科学国家重点实验室, 北京 100101) (2中国科学院大学中丹学院, 北京 100049) (3北京师范大学心理学部, 应用实验心理北京市重点实验室, 心理学国家级实验教学示范中心(北京师范大学), 北京 100875)

序列依赖效应反映了当前的知觉体验不仅取决于当下的刺激输入, 还受到近期历史的影响。这一效应对于我们在动态变化的环境中形成相对稳定的知觉至关重要。本研究使用点阵作为刺激材料, 在数量/面积(实验1)或数量/大小(实验2)两个维度上进行正交设计, 旨在通过估计任务探索任务相关性如何影响线性分布特征的序列依赖效应。结果显示无论特征是否与任务相关, 前一试次与当前试次同一特征总会对当前试次的知觉产生相反的影响。对于任务相关特征, 前一试次产生的序列依赖始终为排斥效应。而对于任务无关特征, 如果在当前试次中无关特征对被试的知觉反应有正向预测作用, 则前一试次无关特征产生排斥的序列依赖效应; 反之, 如果在当前试次中无关特征对被试的知觉反应有负向预测, 则前一试次无关特征产生吸引的序列依赖效应。任务相关性对序列依赖效应的影响主要体现在效应幅值的降低。这些发现揭示了线性分布特征的序列依赖效应受任务相关性以及特征本身特性的共同影响, 而无关特征的序列依赖效应则暗示在客体水平也可以产生序列依赖效应。

序列依赖效应, 数量感, 任务相关性, 线性分布的特征

1 研究背景

我们的感官系统持续从周遭环境中接受大量刺激信息, 这些输入信息往往复杂多变且带有噪声。当这些信息在大脑中加工时, 内部神经元的反应也可能伴随噪声。尽管如此, 我们所感知到的世界仍显得如此非常稳定。那么大脑是如何在瞬息万变的环境中维持对事物连续稳定的知觉呢？近年来研究表明, 人脑可能是通过一种主动过滤掉外源性和内源性噪声的机制以保证对外部世界的稳定知觉。这种过滤机制也被称为序列依赖效应(serial dependence) (Fischer & Whitney, 2014)。

序列依赖效应指的是我们对当前视觉刺激的知觉不仅受到当前刺激本身, 还受到过去知觉经验的影响, 这可能导致对当前刺激知觉的偏差。一般认为这种偏差是吸引的, 使得当前刺激被认为与前一刺激更相似, 但也有研究发现排斥的偏差, 使得对当前刺激的知觉与前一刺激更不同(Cicchini et al., 2017; Fischer & Whitney, 2014; Pascucci & Plomp, 2021; Sun et al., 2020; Xu et al., 2022)。序列依赖效应可能发生在信息处理和表征的各个层面(Cicchini et al., 2021; Fritsche et al., 2017; Xu et al., 2022)。根据当前的各种范式和多项研究结果表明, 序列依赖效应是一种多因素现象, 即先前的感知、记忆、决策和任务的具体要求共同影响对当前刺激特征的决策(Fritsche et al., 2017; Fritsche & de Lange, 2019; Pascucci et al., 2019)。在这种加工机制下, 我们的知觉系统可能保留着最近输入的信息, 使当前的知觉内容系统性地偏向于最近的刺激输入, 从而减少冗余的信息加工和神经噪声。这种内在加工机制被认为是对知觉稳定性的一种解释：过去的经验和当前的刺激输入共同决定了我们当前的知觉。

序列依赖效应广泛存在于各种视觉任务和刺激中, 比如在表征空间上呈圆分布的朝向知觉(Fischer & Whitney, 2014; Fritsche et al., 2017), 颜色估计(Barbosa & Compte, 2020), 圆周空间位置判断(Manassi et al., 2018), 形状知觉(Collins, 2022b)等; 同时, 序列依赖也存在于在表征空间上呈线性分布的特征, 如数量感(Cicchini et al., 2014; Fornaciai & Park, 2018b), 时间知觉(Togoli et al., 2021), 面孔吸引力知觉(van der Burg et al., 2019), 甚至是刺激集合的统计属性, 如变异性(Suárez- Pinilla et al., 2018)。线性分布的特征, 如数量、面积、距离、亮度等, 其值会在一定范围内单向变化; 而圆分布的特征, 如方向、颜色、月份、角度等, 其值在一定范围内变化, 到达上限后会回到起始值, 形成一个循环。有研究者认为, 由于圆分布的数据具有周期性, 它们和线性分布的数据有本质的不同(Cremers & Klugkist, 2018)。鉴于样本空间呈现不同类型的分布形式, 圆分布的数据与线性分布的数据通常需要借助不同的数学模型进行描述, 并采用不同的统计分析方法(Cremers, 2021; Fisher, 1995; Fisher & Lee, 1992; Lagona, 2016; Ravindran & Ghosh, 2011)。

根据以往研究, 圆分布的特征和线性分布的特征在序列依赖效应的方向和强度上, 受到相邻试次间特征物理差异的不同影响。在研究“圆分布”特征的序列依赖效应时, 如朝向特征的研究中, 当先后呈现的两个刺激朝向差异较小时, 被试的反应会系统地偏向于先前试次的朝向, 表现为吸引效应; 而当朝向差异较大时, 则可能没有效应或表现为远离先前试次朝向的排斥效应(Fischer & Whitney, 2014; Fritsche et al., 2017)。这一现象通常使用高斯分布的一阶微分函数或正弦函数来拟合。其他在表征空间上符合圆分布(即：冯·米塞斯分布)的特征在行为表现上也体现出与朝向判断相似的序列依赖效应。然而, 在呈线性分布的视觉特征中存在的序列依赖效应在表现形式上与呈圆分布的不同。比如, 在数量感的研究中, 前一试次的点阵数值越大, 对当前点阵的高估程度越大; 同时, 前一试次的点阵数值越小, 则对当前点阵的低估程度越大。体现出先前数量对当前数量估计的单调影响(Cicchini et al., 2014; Fornaciai & Park, 2020)。这两类特征在序列依赖效应上的差异可能源于我们对二者的表征方式和处理机制可能不同。

虽然线性分布的特征在日常生活中同样普遍, 但与圆分布特征相比, 对线性特征的序列依赖效应研究相对较少。本研究将以数量感及其相关线性特征为研究对象, 考察线性特征的序列依赖效应。数量感是人类和动物的基本数字能力, 在不同物种中普遍存在(杨伟星等, 2017; Cantlon et al., 2009; Kutter et al., 2018), 涉及快速理解、评估和处理数值信息, 以及表征和理解数值之间的关系(Dehaene, 2002)。数量感对很多生物的生存有着重大影响。例如, 鱼会选择更大的鱼群以降低被捕食的风险, 而蜜蜂能够通过花瓣数量来识别花朵(Agrillo et al., 2016; Gross et al., 2009; Pisa & Agrillo, 2009)。此外, 数量感是人类基础的认知能力, 甚至可能是高级数学能力的认知基础(Sadler & Tai, 2007; Starr et al., 2013)。因此, 研究数量感的加工机制尤为重要。

已有多项研究表明, 序列依赖效应的强度和方向受注意和任务相关性影响(Fischer et al., 2020; Fornaciai & Park, 2019a; Fritsche & de Lange, 2019)。有研究发现, 即使在没有明确任务的情况下, 仅通过被动观看刺激也会出现序列依赖效应(Fornaciai & Park, 2018a), 表明任务无关刺激也具有序列依赖效应。Pascucci等人(2019)的研究发现, 被试被明确告知某些试次不需要做朝向的复现报告时, 这些试次的吸引效应消失, 甚至会对后一个试次的朝向知觉产生排斥效应。与之一致的是, 许多的研究证据支持在产生序列依赖效应的过程中, 注意起着至关重要的作用：任务相关的位置或特征会得到更多注意, 其吸引效应也更强。例如, 当多个刺激同时呈现时, 观察者对当前目标位置的光栅朝向的知觉更靠近先前试次中目标位置处的光栅的朝向, 这表明注意位置产生了吸引的序列依赖效应; 但是, 对于先前未被注意的位置(任务无关位置)来说, 吸引的效应减弱甚至出现排斥(Fischer & Whitney, 2014; Fornaciai & Park, 2018b)。除了受空间注意的影响, 序列依赖效应还受到特征注意的影响。即使是同一物体的不同特征(如大小和朝向、颜色和运动方向), 当注意力被引向其中一个特征时, 另一个特征上的序列依赖效应就会大幅减少(Fischer et al., 2020; Fritsche & de Lange, 2019)。

尽管上述实验证据大多支持任务相关性对序列依赖效应的影响, 但是这些研究主要集中于服从圆分布的特征属性, 如朝向或位置。正如前文所述, 线性空间特征的序列依赖效应与圆分布特征表现出不同之处, 其背后的机制可能也有所差异。数量感(numerosity perception)不仅是一项基本的视觉特征, 也是具有代表性的线性空间的特征(Anobile et al., 2012; DeWind et al., 2015; Kutter et al., 2022)。当点阵在数量上不同时, 其他刺激属性, 如点的大小(Item Area, IA)、点的密度(Density)和点阵面积(Field Area, FA)也可能会不同。这些属性之间相互影响, 共同决定了我们知觉到的内容(Franconeri et al., 2009; Harvey et al., 2015; Tokita & Ishiguchi, 2010)。考虑到知觉过程中点阵的不同属性之间可能存在干扰, 这种干扰是否会进入刺激的历史信息, 进而体现在序列依赖效应中？当作为任务无关特征和任务相关特征时, 不同刺激属性的序列依赖效应又将分别呈现出什么特点？

到目前为止, 仅有少数团队和研究尝试探讨数量感及其相关特征之间的序列依赖效是否受任务相关性的影响。例如, 基于数量感和时间知觉的研究发现, 当这两种特征分别作为无关特征时, 对另一特征均不具有吸引效应(Togoli et al., 2021)。此外, 数量和点阵中单个点的平均面积大小也只在作为任务相关特征时影响自身的序列依赖效应(Fornaciai et al., 2023)。利用事件相关电位技术(event−related potentials, ERP)的研究发现, 虽然行为上数量和大小都没有体现出跨特征的序列依赖效应, 神经信息中却能够解码出它们作为无关特征时的表征(Fornaciai et al., 2023)。

尽管上述以数量感为研究对象的研究已尝试探讨线性特征的序列依赖效应受任务相关性的影响, 但它们所使用的研究范式与经典的序列依赖效应研究范式存在区别。在研究圆分布的特征的序列依赖效应时, 常采用复现/估计任务(Adjustment tasks) (Cicchini et al., 2018; Fischer & Whitney, 2014), 如经典的朝向复现范式, 而“线性表征”的特征(如数量感)的序列依赖效应研究多采用迫选任务(Forced-choice tasks) (Cicchini et al., 2021; Fornaciai & Park, 2018b, 2019b, 2020)。复现/估计任务要求被试调整反应工具, 使之尽量与他们知觉到的刺激特征匹配。迫选任务通常是让被试需要比较目标刺激和参考刺激的某一特征(如朝向、数量) (Cicchini et al., 2021; Fritsche et al., 2017), 通过心理物理曲线的偏移来揭示诱导刺激是否改变了目标刺激的知觉特征。

复现/估计任务与迫选任务主要有以下区别。首先, 迫选任务主要关注同一试次中诱导刺激对探测刺激知觉的影响(Fornaciai & Park, 2018b, 2019b; Togoli et al., 2021)。在该范式下, 被试不需要对诱导刺激本身进行知觉报告, 因此任务无关特征的知觉加工并没有被特别明确地抑制, 对诱导刺激的知觉加工是否准确或加工到什么程度也无法明确得知。然而在复现/估计范式中, 被试对前后两个试次的刺激的任务相关特征都需要进行报告, 可以最大程度上减小无关特征的知觉加工。其次, 相对于估计任务, 迫选任务对认知加工的要求更少, 被试不一定需要完成从非符号到符号的转换。复现/估计任务则更多涉及到记忆等更为高级的知觉阶段。最后, 经典的复现/估计范式中, 先前试次刺激的特征往往具有多个水平; 而在以往迫选任务中, 诱导刺激的特征水平数较少, 这可能限制了其实验效度。综上所述, 为了直接比较线性特征与圆分布特征的序列依赖效应, 并排除掉实验范式等混淆因素的潜在影响, 我们选用复现/估计任务对数量感的序列依赖效应进行考察。

本研究旨在应用经典的序列依赖效应研究范式, 并通过数量估计和面积估计两种任务, 探究任务相关性如何影响线性特征的序列依赖效应及其作用机制。在数量感的序列依赖效应研究中, 通常会呈现一系列点阵, 要求被试估计点阵中点的数量或者分辨哪一个点阵包含的点的数量更多(Castaldi et al., 2018; Cicchini et al., 2014; Fornaciai & Park, 2018b, 2020)。本研究同样采用点阵作为刺激材料, 其中点的数量与点阵面积(实验1)或者点的数量与点的大小(实验2)两个维度正交变化。前人研究发现, 先前刺激的物理特征和被试的反应都会影响当前的判断, 且放在同一模型中相比逐一单独考虑时, 二者表现出来的序列依赖效应有很大的差异(Shan & Postle, 2022; Stern et al., 2022)。本研究以刺激的物理特征和被试反应中的一个或多个因素分别作为自变量, 建立广义线性混合效应模型(Generalized Linear Mixed-effects Models, GLMM)。GLMM作为一种强大的统计工具, 能够处理不同的响应变量分布, 使得模型更加灵活。它可以同时考虑固定效应和随机效应的影响, 从而更好地处理被试之间的个体差异和实验设计中的复杂交互效应, 因此可以提供更精确和稳健的估计结果(Bolker et al., 2009)。我们将通过模型比较来确定最优模型, 并进一步分析该模型中刺激的物理特征和被试反应对序列依赖效应的贡献。

2 实验1：数量与点阵面积的任务相关性对序列依赖效应的影响

2.1 实验目的

本实验采用估计任务, 评估数量和面积估计中序列依赖效应的行为特征, 以及数量和面积分别作为任务无关特征时, 对后续面积或数量的知觉的影响。预期在估计任务中, 任务相关性会影响序列依赖效应。在数量估计任务中, 由于数量是任务相关特征, 其序列依赖效应应该更强, 而面积作为任务无关特征, 其序列依赖效应应该较弱。在面积估计任务中则相反。

2.2 方法

2.2.1 被试

本研究采用G*power 3.1.9软件(Faul et al., 2009), 设置Effect size2为0.3, Power (1 − β)为80%, α水平为0.05, 计算出所需样本量为29人。实验1实际招募33名被试, 其中包括25名女性, 平均年龄21.15岁, 均为北京师范大学在校学生, 所有参与者视力或矫正视力正常, 无色盲、色弱, 右利手。他们均非数学专业, 非心理学专业大二及以上年级。本研究通过北京师范大学心理学部实验伦理审查, 并支付被试相应实验费用。

2.2.2 实验仪器与材料

实验在安静且黑暗的房间内进行, 显示器为27英寸纯平彩色显示器, 垂直刷新频率59 Hz, 分辨率2560×1440, 实验时屏幕背景色为灰色, 亮度为10 cd/m2。被试距离计算机屏幕55 cm。实验材料为黑色实心小圆点和白色实心小圆点构成的点阵。点阵使用CUSTOM生成(de Marco & Cutini, 2020), 在点的数量和点阵面积两个维度上正交变化。点阵呈现在以屏幕中央为圆心的圆形区域内。点阵中点的个数有7个水平, 分别是8, 10, 12, 16, 20, 26, 或32个点。为保证光通量相等, 点阵中黑点和白点的数量相等, 各占二分之一。点阵面积也具有7个水平, 分别为40.1 degree2, 50.1 degree2, 60.1 degree2, 80.2 degree2, 100.2 degree2, 130.3 degree2或160.3 degree2。每个点的面积大小的范围是0.04 degree2到0.28 degree2; 每个点阵中点的平均面积大小(所有点的面积之和除以点的个数)为0.16 degree2。实验时以图片形式呈现不同点阵, 每个水平下生成20张不同的点阵图片, 共980张, 每次呈现目标刺激均为从对应水平的图片中不放回地随机调用一张图片。实验流程的实现和反应数据的记录由MATLAB (Matlab R2018b, The Mathworks, Inc., Natick, Massachusetts, USA)软件和Psychotoolbox−3插件(Brainard, 1997)控制完成。

2.2.3 实验设计与流程

实验采用7×7×2的组块设计, 每位被试参与了所有实验条件的测试。三个自变量分别是：(1)点阵中点的数量, 范围在8～32个点, 共7个水平; (2)点阵的面积, 范围在40.1 degree2～ 160.3 degree2, 也是7个水平; (3)任务相关性：数量估计任务中被试被要求注意点阵中点的数量, 此时数量为任务相关特征, 面积为任务无关特征; 面积估计任务中被试需要注意点阵的面积, 此时面积为任务相关特征, 点的数量为任务无关特征。两个任务的顺序在被试间进行了平衡。被试对任务相关特征的估计值被记录下来。

以数量估计实验为例, 实验流程如图1所示：(1)首先在屏幕中央呈现一个黑色十字注视点1350 ms ～ 1450 ms, 要求被试始终注视中央十字点位置; (2)接着呈现刺激图片, 每次在屏幕中央呈现一个点阵, 持续时间250 ms; (3)然后在屏幕上方呈现任务指导语“请尽量准确地估计点的个数”一行字, 并且在指导语下方呈现数轴, 数轴两端分别标有“5”和“40”刻度, 被试用鼠标在数轴上点击后, 点击位置会出现一条白色刻度线, 刻度线下方显示此处对应的数值。实验前告知被试反应阶段没有时间限制, 要求被试尽可能准确地估计, 被试可进行多次点击, 直至按下回车键确认, 记录此时的刻度值, 即为被试对点数的估计值。被试有15 s的反应时间, 超出15 s未按下回车键, 程序会自动进入下一试次, 该试次被试的反应为“N/A”。指导语和数轴位置均在刺激图片的上方, 和点阵呈现的位置不重叠。

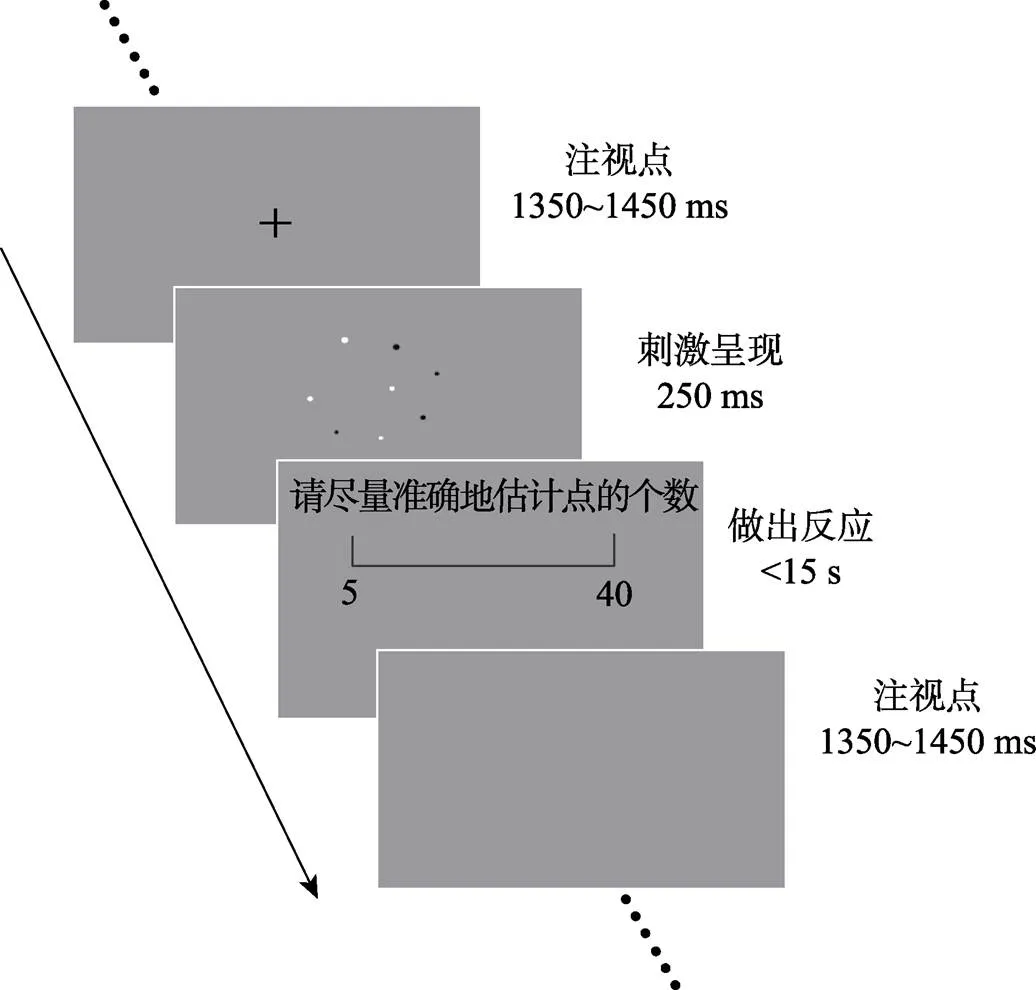
图1 实验流程图(以数量估计任务为例)。注视点即为试次间时间间隔, 为了防止被试产生预期, 间隔在1350～1450 ms间随机取样。实验前告知被试一定要尽量准确的估计。为了避免被试注意力分散长时间不反应, 15 s后将自动进入下一试次, 本试次被试的反应记录为N/A。

实验分为数量估计实验和面积估计实验两部分进行, 在每种任务条件下, 所有实验水平均随机呈现。整个实验共588个试次, 分为6个组块。每个任务包含3个连续的组块, 每个组块包含98个试次。实验任务的顺序在被试间平衡。每个实验任务开始之前, 被试均需要进行练习。一组练习为15个试次, 根据被试的表现练习2～3组, 数量估计任务的平均估计误差小于5, 面积估计任务的平均估计误差小于25 cm2视为通过练习。完成整个实验大约需要110分钟。

2.2.4 数据分析

实验数据采用MATLAB R2018b软件分析, 首先将单个任务下每个被试所有试次进行整合, 剔除没有记录到被试反应的试次。根据韦伯-费希纳定律可知, 对物理刺激的心理表征呈对数形式。所以本研究将所有试次中点的数量、点阵面积和被试的估计值以2为底数进行对数化。为统一数量和面积的单位进行量化分析, 进一步将对数化后的数量和面积属性进行标准化, 根据物理刺激中数量或面积的均值和标准差对被试的估计值进行标准化。

为了检验当前相关特征、当前无关特征、前一试次相关特征、前一试次无关特征和前一试次估计值对被试当前估计值的影响, 我们建立了4个GLMMs (Zhang & Luo, 2023)。根据以往文献, 前一试次估计值对当前估计值有一致较强的吸引效应(Moon & Kwon, 2022; Pascucci et al., 2019), 因此, 为了提高模型的解释能力, 在所有的GLMMs中, 我们都将前一试次估计值与当前相关特征放进来作为自变量, 另外三个因子分别进入到模型中。模型1假设前一试次相关特征影响当前估计值, 即任务相关特征的序列依赖效应。模型2假设当前无关特征对当前估计值有影响, 即同一客体的不同特征之间的相互影响。模型3假设前一试次任务无关特征会影响当前估计值, 即任务无关特征产生的序列依赖效应。模型4为全模型, 假设5个因子都对当前估计值有所贡献, 共同影响被试的决策。混合效应模型同时考虑了自变量在群体水平的固定效应和由于被试之间的差异而产生的随机效应。以数量任务为例, 模型4表达式为：

Y=0i+1iCurrentNumerosity+

2iPreviousResponse+3iPreviousNumerosity

+4iCurrentArea+5iPreviousArea(1)

0i=0+0i;1i=1+1i;2i=2+2i;3i=3+3i;

4i=4+4i;5i=5+5(2)

其中,代表第i个被试,代表当前任务下的第j个试次,Y代表第i个被试在第j个试次中的估计值。表示组水平效应的系数,代表个体水平随机效应。

2.3 实验结果

为了比较当前无关特征、前一试次相关特征和前一试次无关特征对当前试次的知觉的影响大小, 我们将所有被试的所有试次合并在一起进行回归分析, 建立了4种GLMMs, 模型1：包含了前一试次相关特征、当前试次相关特征和前一试次知觉估计值; 模型2：包含了当前无关特征、当前相关特征和前一试次估计值; 模型3：包含了前一试次无关特征、当前相关特征和前一试次估计值; 模型4：包含了前一试次相关特征、当前无关特征、前一试次无关特征、当前相关特征和前一试次估计值。通过计算和比较4个模型的贝叶斯信息准则(bayesian information criterion, BIC)值来确定最优的模型。BIC不仅考虑了模型的拟合优度, 还考虑了模型的复杂度, 可以帮助我们在模型拟合优度和模型复杂度之间找到一个平衡, 尽量避免过拟合的问题。相比于其他模型选择准则, BIC对模型复杂度的惩罚更大, 因此在样本量较大时, BIC可以提供更稳健的模型选择结果(Burnham & Anderson, 2004)。结果如表1所示, 无论是在数量估计任务还是面积估计任务中, 模型4(全模型, Full model)的表现都是最优的(数量任务：模型1～4的BIC分别为8533、8158、8589、8052; 面积任务：模型1～4的BIC分别为11713、10882、11838、10713), 即在两种任务下, 当前无关特征、前一试次相关特征和前一试次无关特征的信息都对当前试次的知觉估计有贡献。

我们同时还使用均方误差(Mean Squared Error, MSE) (如表2所示)作为模型比较的指标, 得到了一致的结果, 模型4仍然具有最优表现。

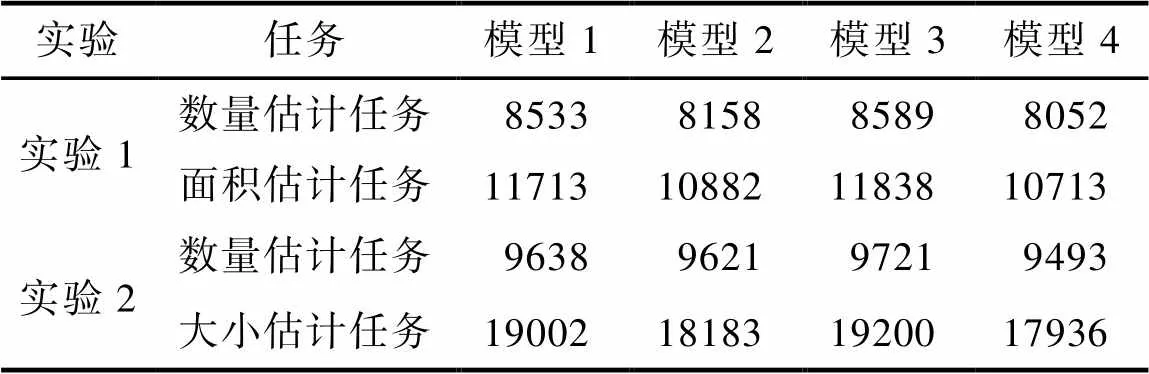
表1 各模型BIC值

表2 各模型MSE值

进一步检验胜出模型(模型4)中各变量的回归系数, 考察各个因素对当前估计的序列依赖效应的大小和方向。如图2a所示, 数量估计任务中, 当前点阵中点的个数(即：当前相关特征)、点阵面积(即：当前无关特征)、以及前一试次的知觉估计值均正向预测了被试对当前试次刺激特征的知觉(当前相关特征：回归系数值β = 0.76, 95% CI = [0.75, 0.77],(9561) = 203.94,< 0.001; 当前无关特征：β = 0.08, 95% CI = [0.07, 0.09],(9561) = 21.47,< 0.001; 前一试次知觉估计值：β = 0.19, 95% CI = [0.17, 0.21],(9561) = 19.07,< 0.001); 而前一个试次中点阵的数量和面积都与当前试次的知觉呈负相关, 即先前刺激特征的序列依赖效应均为排斥作用(前一试次相关特征：β = −0.09, 95% CI = [−0.10, −0.07],(9561) = −10.33,< 0.001; 前一试次无关特征：β = −0.02, 95% CI = [−0.03, −0.02],(9561) = −6.23,< 0.001)。

在面积估计任务中, 各变量对当前试次知觉的影响方向与数量估计任务一致, 也表现为当前刺激的任务相关特征、任务无关特征以及前一试次的估计值均与当前知觉估计值呈正相关(当前相关特征：回归系数值β = 0.64, 95% CI = [0.63, 0.65],(9553) = 149.70,< 0.001;当前无关特征：β = 0.14, 95% CI = [0.13, 0.15],(9553) = 32.22,< 0.001; 前一试次知觉估计值：β = 0.22, 95% CI = [0.20, 0.24],(9553) = 21.70,< 0.001), 而前一试次的相关和无关特征产生的序列依赖效应均为排斥作用(前一试次相关特征：β = −0.11, 95% CI = [−0.12, −0.09],(9553) = −13.79,< 0.001; 前一试次无关特征：β = −0.02, 95% CI = [−0.03, −0.01],(9553) = −4.21,< 0.001)。

图2 (a)实验1两个任务全模型的各自变量的回归系数(β)值。CurRF (Current Relevant Feature)为当前任务相关特征, 例如在数量估计任务中是指当前刺激点阵中点的个数; PreRF (Previous Relevant Feature)为前一试次任务相关特征, 例如在数量估计任务中是指上一试次的刺激点阵中点的个数; CurIRF (Current Irrelevant Feature)为当前任务无关特征, 例如在数量估计任务中是指当前刺激点阵的面积; PreIRF (Previous Irrelevant Feature)为前一试次任务无关特征, 例如在数量估计任务中是指上一试次的刺激点阵的面积; PreRes (Previous Response)为前一试次被试估计值, 例如在数量估计任务中是指被试对上一试次中刺激点阵的点的个数的估计值。图中误差线代表β值的一倍标准误(Standard Error, SE); (b)实验2两个任务全模型的各自变量的回归系数(β)值。

2.4 讨论

无论是在数量估计任务还是在面积估计任务中, 全模型的表现均为最优。这说明对于点阵中数量和面积这两个属性而言, 当前无关特征、先前相关特征、先前无关特征和先前知觉估计值都对当前试次的知觉决策有显著影响。一方面, 结果体现了同一客体的不同属性之间在表征时会相互影响, 即使是未被要求注意的特征, 也能够影响被试对当前任务相关特征的表征; 另一方面, 结果表明对于线性分布的特征, 先前的无关特征仍具有序列依赖效应, 但相比与任务相关特征, 任务无关特征的贡献较小。

在序列依赖效应的方向上, 本研究发现前一试次的知觉估计对当前试次的知觉估计有吸引效应, 而前一试次刺激的物理特征则对当前试次的知觉有排斥效应。这两种不同方向的偏差可能涉及不同加工水平在不同时间尺度上的表现, 知觉决策被最近的知觉决策吸引, 同时被最近的物理特征值排斥(Gekas et al., 2019; Moon & Kwon, 2022; Schwiedrzik et al., 2014)。

数量和面积是量感理论中关系非常密切的两种属性。这种无关特征引起的序列依赖效应是否源于这两种属性之间特殊的关系, 还是普遍存在于数量感与其他非数量属性之间？比如, 点阵中单个点的平均大小。点的平均大小是一个关键的统计属性, 用于衡量点阵中圆点占据视网膜的区域, 对被试的表征过程提出了更高的认知挑战, 因为它涉及到对视觉输入的综合评价和加工。作为任务无关特征时, 先前点阵中点的数量是否依然会影响当前试次点大小的判断, 同时, 未被注意的点的大小属性又是否会影响被试对当前数量的表征？为了探究这一问题, 我们设计了实验2。

3 实验2：数量与点大小的任务相关性对序列依赖效应的影响

3.1 实验目的

为了探究实验1发现的任务相关性对线性特征的序列依赖效应的影响是否特定于数量感和面积, 还是线性特征中的一般现象, 实验2选择数量和单个点的平均大小作为研究对象, 探究大小属性的序列依赖效应的行为特征, 以及任务相关性对序列依赖效应的调节作用。我们仍然采用估计任务, 以评估面积和数量之间存在的任务无关特征的序列依赖效应能否泛化到其他数量相关特征中, 如果可以, 表现形式是否一致。预期与实验1中类似, 任务相关性会影响序列依赖效应。在数量估计任务中, 由于数量是任务相关特征, 其序列依赖效应应该更强; 而点的平均大小作为任务无关特征, 其序列依赖效应应该较弱。在大小估计任务中则相反。

3.2 方法

3.2.1 被试

和实验1标准一致, 本实验也需要样本量29人, 实验2实际招募到34名被试, 其中有25名女性, 平均年龄21.24岁, 均为北京师范大学在校学生, 视力或矫正视力正常, 无色盲、色弱, 右利手, 非数学专业, 非心理学专业或者心理学大一同学。本研究通过北京师范大学心理学部实验伦理审查, 并支付被试相应实验费用。

3.2.2 实验仪器与材料

实验在安静黑暗的房间内进行, 被试距离计算机屏幕55 cm, 实验材料为黑色实心小圆点和白色实心小圆点构成的点阵。点阵是以屏幕中央为圆心, 到距离最远的点为半径画的圆形区域, 同样使用CUSTOM生成, 在点的数量和点的平均面积两个维度上正交变化。点阵中包含8, 10, 12, 16, 20, 26, 或32个点, 为保证光通量相等, 点阵中黑点和白点的数量相等, 各占二分之一。点阵面积为80.2 degree2, 每个点阵中点的平均面积, 即所有点的面积之和除以点的个数, 为0.04 degree2, 0.05 degree2, 0.06 degree2, 0.08 degree2, 0.1 degree2, 0.13 degree2或0.16 degree2, 每个点的面积为大小的0.25～1.75倍。其余设置与研究一一致。

3.2.3 实验设计与流程

实验采用7×7×2的block设计, 每名被试参与了所有实验条件的测验。3个自变量分别是：(1)点阵中点的数量, 范围在8～32个点, 共7个水平; (2)点的平均大小, 范围在0.04 degree2～ 0.16 degree2, 同样为7个水平; (3)任务相关性：数量估计任务中被试被要求注意点阵中点的数量, 此时数量为任务相关特征, 大小为任务无关特征。大小估计任务中被试需要注意点阵中所有点的平均面积大小, 此时大小为任务相关特征, 点的数量为任务无关特征。两个任务的顺序在被试间平衡。实验的因变量是被试对任务相关特征的估计值。

实验2的实验流程与数据分析方法与实验1相同, 只是其中的面积估计任务改为大小估计任务。

3.3 实验结果

与实验1相同, 我们把同一任务下每个被试的所有试次合并在一起, 以进行回归分析, 建立了与实验1相同的4个GLMMs, 通过分别计算4个模型的BIC值以决定哪个模型最优。无论是在数量估计任务还是大小估计任务中, 依旧是包含了当前无关特征、前一试次相关特征和前一试次无关特征的信息的模型4最优(表1), 其BIC值远低于前三个模型(数量任务：模型1～4的BIC分别为9638、9621、9721、9493; 大小任务：模型1～4的BIC分别为19002、18183、19200、17936)。这表明在对数量的估计和大小的估计中, 被试综合运用了当前无关特征、前一试次相关特征和前一试次无关特征的信息。

进一步检验胜出模型(模型4)中各变量的回归系数, 以考察各个因素对当前试次知觉估计的序列依赖效应的大小和方向。模型4中各变量的回归系数如图2b所示。在大小估计任务中, 与实验1的发现一致, 当前特征的任务相关特征、任务无关特征和前一试次知觉估计值均与当前试次知觉估计呈正相关(当前相关特征：β = 0.84, 95% CI = [0.83, 0.85],(9868) = 140.41,< 0.001;当前无关特征：β= 0.20, 95% CI = [0.19, 0.21],(9868) = 33.28,< 0.001; 前一试次知觉估计值：β = 0.29, 95% CI = [0.27, 0.31],(9868) = 30.00,< 0.001), 前一试次特征产生的序列依赖效应则为排斥作用(前一试次相关特征：β = −0.16, 95% CI = [−0.18, −0.14],(9868) = −16.43,< 0.001; 前一试次无关特征： β = −0.03, 95% CI = [−0.04, −0.02],(9868) = −4.50,< 0.001)。

在数量估计任务中, 当前点阵中点的个数和前一试次知觉估计值均与当前试次的数量知觉呈正相关(当前相关特征：β = 0.74, 95% CI = [0.73, 0.75],(9835) = 188.37,< 0.001; 前一试次知觉估计值：β = 0.22, 95% CI = [0.20, 0.23],(9835) = 22.29,< 0.001)而当前点阵中大小与当前试次的数量知觉呈负相关(当前无关特征：β = −0.04, 95% CI = [−0.05, −0.04],(9835) = −11.21,< 0.001); 前一个试次中点阵的数量与当前试次的数量知觉呈负相关, 即相关特征的序列依赖效应为排斥作用(前一试次相关特征：β = −0.09, 95% CI = [−0.10, −0.07],(9835) = −10.33,< 0.001), 而前一试次中点的大小这一无关特征的序列依赖效应则为吸引作用(前一试次无关特征：β= 0.02, 95% CI = [0.02, 0.03],(9835) = 5.89,< 0.001)。结合实验1, 当前试次刺激的某一特征对当前试次知觉决策的影响与前一试次的该特征产生的序列依赖效应作用的方向是相反的, 即如果某个特征与当前知觉估计值呈正相关, 则其在后一试次的知觉估计上会产生负向的序列依赖效应; 反之, 如果与当前知觉估计值呈负相关, 则在后一试次上产生正向的序列依赖效应。

3.4 讨论

与实验1的发现一致, 无论是数量估计任务还是大小估计任务, 前一试次的知觉估计对当前试次的知觉均存在吸引效应, 并且无论是任务相关特征还是任务无关特征, 其前一试次的特征物理值都对当前试次的知觉有影响。前一试次任务相关特征对当前试次的知觉呈现排斥效应。前一试次任务无关特征的影响表现为：数量作为无关特征对当前试次点平均大小的知觉的影响为排斥效应, 而前一试次点平均大小作为无关特征时, 对当前试次数量的知觉则具有吸引效应。由此可见, 数量和单个点的大小分别作为无关特征时, 对彼此的序列依赖效应具有不对称性。这种不对称性可能与两种刺激特征之间本身特性的关系有关。

4 讨论

本研究以数量感为研究对象, 通过数量和面积的估计任务、以及数量和点平均大小的估计任务这两个实验, 考察了任务相关性对线性特征的序列依赖效应的影响。两个实验中, 广义线性混合效应模型比较的结果均一致支持, 除当前试次任务相关特征和前一试次知觉估计之外, 当前无关特征、前一试次相关特征和前一试次无关特征也都对当前试次的知觉决策有显著贡献。进一步检验上述各个因素的回归系数, 在两个实验中一致发现, 无论特征是否与任务相关, 前一试次的该特征与当前试次同一特征对当前试次的知觉的影响总是呈现反向关系。对于任务相关特征, 前一试次产生的序列依赖效应总是排斥效应; 而对于任务无关特征, 前一试次该特征产生的序列依赖效应是吸引还是排斥效应, 则取决于该特征本身的性质：数量作为无关任务特征时, 无论当前任务特征是点阵面积还是单个点平均大小, 其序列依赖效应总是排斥效应; 点阵面积作为无关任务特征时, 其序列依赖效应也是排斥的; 而单个点平均大小作为无关特征时, 其序列依赖效应则是吸引的。

前一试次的任务相关特征对当前知觉的排斥效应与经典研究中发现的吸引的序列依赖效应恰好相反(Cicchini et al., 2018; Fischer & Whitney, 2014; Xia et al., 2016)。这应该与本研究中同时考虑了前一试次的知觉估计对当前试次知觉的序列依赖效应有关。先前研究已发现, 前一试次中被试的行为反应与刺激物理值对随后试次中知觉的影响存在差异。Pascucci等人(2019)的研究中, 被试对某些试次不需要对目标进行报告, 在这些试次中, 刺激对于后续知觉的影响表现为排斥效应, 相反, 当需要进行知觉报告时, 其对于后续知觉的影响则是吸引的。此外, 由于迫选任务被认为是一种更直接的感知测量方法, 作者还使用迫选任务代替了朝向复现范式(被试不需要报告刺激的准确朝向, 只需要报告目标刺激的朝向是更接近垂直方向还是水平方向), 结果再次证实刺激本身引起排斥效应, 而被试的反应则引起吸引效应。Moon和Kwon (2022)把经典研究中发现的刺激的吸引性序列依赖效应归因于它与被试反应的高相关性, 在分别固定知觉朝向和特征的物理朝向后, 发现当固定知觉朝向时, 物理朝向的序列依赖效应是排斥的, 而先前反应的序列依赖效应仍然是吸引的。Sadil等(2021)则采用了同时考虑前一试次刺激和反应的双因素分析取代了经典序列依赖效应研究中常用的单因素分析(仅考虑前一试次的刺激值), 对这些经典研究的数据进行重新分析, 一致发现刺激的序列依赖效应是排斥的, 而反应的序列依赖效应则是吸引的。因此, 经典研究中刺激的吸引性序列依赖效应可能与其未考虑上一试次被试的反应这一因素有关。以上研究证据以及本研究发现的任务相关特征的排斥序列依赖效应, 均支持先前试次对当前知觉的吸引效应主要来自于先前试次的知觉反应, 而排斥效应则主要来自于先前试次刺激特征的物理值。序列依赖效应在刺激和反应水平的方向是相反的, 这可能体现了视觉系统在加工外界刺激时需要在对外界信息的敏感度和过去经验的依赖性之间进行权衡和调节(Pascucci et al., 2019)。在知觉和认知过程中, 我们需要处理和加工各种刺激, 平衡敏感度和经验依赖性。过于敏感会干扰注意力和认知, 过于依赖过去的经验会导致忽略新信息。需要根据任务灵活调整敏感度和经验依赖之间的平衡, 如清晰任务需更敏感, 而处理复杂任务需更依赖经验。这种平衡可以帮助提高我们的知觉和认知表现。

本研究发现, 即使是与任务无关的线性特征, 也表现出明显的序列依赖效应, 从而为客体水平上序列依赖效应的存在提供了支持。一般认为, 客体是一个由一系列特征整合而成的可数的实体(Adelson & Bergen, 1991; Pascucci et al., 2023), 通常具有时空连续性(Kahneman et al., 1992)。客体档案(Object file)被认为是知觉、注意和工作记忆等信息加工的基本单元。若知觉构建在客体基础上, 那么过往知觉经验对当前知觉的影响, 是基于客体还是特征水平呢？Collins (2022a) 提出了两种理论假设。第一种理论主张序列依赖直接发生在基本的视觉特征水平。如果序列依赖作用发生在低水平的特征加工阶段, 预计跨特征的序列依赖效应不会出现。第二种理论认为序列依赖效应可能发生在客体水平。关注一个客体的单一特征, 比如颜色, 会使得注意力集中, 同时该客体的其他特征也会进入注意的焦点, 从而提高客体表征的质量和效率(Kahneman et al., 1992; Printzlau et al., 2022; Zhou et al., 2016)。如果该假设成立, 预期不同客体间相同特征的序列依赖效应将消失; 同时, 同一客体的不同特征之间应存在相互影响。基于客体的序列依赖效应在圆分布特征的序列依赖效应研究中获得了验证。Liberman等人(2016)利用客体的时空连续性证明了基于客体的序列依赖效应。具体来说, 他们发现只有当光栅以连贯的运动穿过屏幕上的遮挡物, 而不是在遮挡物上不连贯移动或静止在遮挡物两侧时, 被试对最后一个光栅的朝向知觉才会受前面光栅朝向的影响。Kramer和Jacobson(1991)的研究则发现, 相较于在不同客体上的情况, 目标和干扰子在同一客体上时, 被试搜索到目标的反应速度和准确度更高。Liberman等人(2014)的研究揭示, 即便在客体保持不变而其特征发生变化的情况下, 例如面部观察角度的改变, 仍会引发序列依赖效应。另外, 当要求被试判断面孔表情是厌恶还是高兴时, 面孔性别的变化被发现能够显著地削弱情绪的序列依赖效应(Collins, 2022a)。此外, Fritsche和de Lange (2019)的研究发现, 尽管在判断前一个光栅的大小任务中, 相对于朝向判断任务, 被试对当前光栅的朝向知觉的序列依赖效应减弱, 但仍然显著存在。这说明即使当前任务要求被试选择性注意特定的目标特征(如大小), 属于该客体的其他特征(如朝向)并没有因为其与任务无关被完全过滤, 而仍然被知觉或者记忆, 从而影响对后续刺激的知觉加工。这些研究一致的支持了基于客体的序列依赖现象的存在。

我们发现虽然任务无关的线性特征具有序列依赖效应, 但该效应较任务相关特征明显更小。这也与以往研究注意或者任务相关性对圆分布特征序列依赖效应影响的发现一致。Flesch等人(2022)使用叶片形状和分叉枝条个数分别作为任务相关或无关特征, 研究大脑额顶叶皮层对于二者的表征解码时, 发现无关特征具有压缩表征的特性, 特征的不同水平之间表征相似度很高; 而相关特征不同水平的表征则区别较明显。这可能是因为将无关特征的表征压缩到一个低维空间中可以减少冗余信息和干扰, 从而提高特征的区分度和鲁棒性, 使大脑更加高效稳定地处理任务。

任务无关特征的序列依赖效应的方向的差异表明, 这种效应还与特征本身的特性密切相关。研究发现, 当数量作为无关任务特征时, 无论当前任务相关特征是点阵面积还是单个点平均大小, 数量的序列依赖效应总是排斥的。点阵面积作为无关任务特征时, 其序列依赖效应也是排斥效应。然而, 仅在单个点平均大小作为无关特征时, 产生的是吸引的序列依赖效应。所有任务中的一致发现是, 虽然前一试次无关特征对当前知觉的序列依赖效应因特征而异, 但是该效应总与它们作为当前试次无关特征时的影响方向相反。前一试次无关特征的序列依赖效应可能与特征之间相互作用的方式有关。例如, 当任务无关特征(例如面积)在数量空间里与数量特征同向变化时(DeWind et al., 2015), 其对数量的影响在当前试次表现为吸引, 而在前一试次表现为排斥; 相反, 当任务无关特征(例如平均大小)在数量空间里与数量特征反向变化时(DeWind et al., 2015), 该特征对数量的影响则是当前试次排斥, 前一试次吸引。不过该假设的验证和具体机制还有待将来的进一步研究。

以往研究中也发现无关特征的特性本身或者它与相关特征之间的关系会影响序列依赖效应。Liberman等人(2018)发现, 情绪判断中的序列依赖效应在改变面孔性别后会消失, 而在改变面孔种族后则仍然存在, 这表明性别差异在面孔之间产生的不相似性比种族更大。在Fornaciai和Park(2019a)的一项研究中, 尽管数量感和闪光次数存在吸引的序列依赖效应, 但数量感和声音播报的次数分别作为任务无关特征时则不对彼此产生显著的序列依赖。此外, 当背景刺激的颜色变化与任务无关时, 序列依赖效应不受背景特征的影响, 对当前朝向的决定独立于刺激背景中的颜色变化, 只系统地偏向于先前刺激的朝向(Fischer et al., 2020)。特征之间的加工关系分为独立表征和整合表征(Leibovich et al., 2017; Lourenco & Aulet, 2023)。独立加工的特征在知觉上表现为不同特征维度之间的相互独立。这意味着, 当我们感知一个物体时, 我们可以独立地处理其不同的特征, 例如颜色、形状、大小和方向。这些研究中朝向和大小分别拥有独立的加工机制, 由不同的脑区负责加工, 因此两种特征之间不会产生序列依赖效应。而来自神经影像学、计算模型、视觉错觉和心理物理学的证据, 证明非数字的幅值, 如累计面积, 是与数字一起编码的, 并在整个视觉知觉中持续存在, 它们之间的交互作用可能会影响到数字感知本身, 例如数字大小的感知可能会受到物体大小或形状的影响(Harvey et al., 2015)。当这些特征作为任务无关特征时, 依然会影响当前任务相关特征的序列依赖效应。因此, 考察任务相关性对特征的序列依赖效应的影响时, 特征间是否具有独立的加工过程也是影响该效应方向的重要因素。

综上所述, 本研究探讨了任务相关性对线性特征的序列依赖效应的影响。研究结果显示, 对于线性分布的特征, 先前的无关特征仍表现出序列依赖效应, 尽管其影响程度相较于任务相关特征较小。这一发现揭示了同一客体内不同属性的知觉表征之间存在相互影响, 即使是未被明确要求注意的特征, 也能够影响对当前任务相关特征的知觉。此外, 跨特征的序列依赖效应的存在支持了序列依赖效应可以发生在客体水平的假设。未来研究可以进一步结合功能磁共振成像等技术, 深入探索数量感中跨特征序列依赖效应的神经基础以及该效应的表征模式。

Adelson, E. H., & Bergen, J. R. (1991). The plenoptic function and the elements of early vision. In M. S. Landy & J. A. Movshon (Eds.),(pp. 3−20). The MIT Press.

Agrillo, C., Petrazzini, M. E. M., & Bisazza, A. (2016). Number versus continuous quantities in lower vertebrates. In A. Henik (Ed.)(pp. 149−174). Academic Press. https://doi.org/10.1016/ B978-0-12-801637-4.00007-X

Anobile, G., Cicchini, G. M., & Burr, D. C. (2012). Linear mapping of numbers onto space requires attention.,(3), 454−459. http://doi.org/10.1016/j. cognition.2011.11.006

Barbosa, J., & Compte, A. (2020). Build-up of serial dependence in color working memory.,(1), 10959. http://doi.org/10.1038/s41598-020-67861-2

Bolker, B. M., Brooks, M. E., Clark, C. J., Geange, S. W., Poulsen, J. R., Stevens, M. H. H., & White, J. S. S. (2009). Generalized linear mixed models: A practical guide for ecology and evolution.(3), 127−135.

Brainard, D. H. (1997). The psychophysics toolbox.(4), 433−436.

Burnham, K. P., & Anderson, D. R. (2004). Multimodel inference: Understanding AIC and BIC in model selection.(2), 261−304. https://doi.org/10.1177/0049124104268644

Cantlon, J. F., Platt, M. L. & Brannon, E. M. (2009). Beyond the number domain.(2), 83−91.

Castaldi, E., Mirassou, A., Dehaene, S., Piazza, M., & Eger, E. (2018). Asymmetrical interference between number and item size perception provides evidence for a domain specific impairment in dyscalculia.,(12), e209256. http://doi.org/10.1371/journal.pone.0209256

Cicchini, G. M., Anobile, G., & Burr, D. C. (2014). Compressive mapping of number to space reflects dynamic encoding mechanisms, not static logarithmic transform.,(21), 7867−7872. http://doi.org/10.1073/pnas.1402785111

Cicchini, G. M., Benedetto, A., & Burr, D. C. (2021). Perceptual history propagates down to early levels of sensory analysis.,(6), 1245−1250.

Cicchini, G. M., Mikellidou, K., & Burr, D. (2017). Serial dependencies act directly on perception.,(14), 6. http://doi.org/10.1167/17.14.6

Cicchini, G. M., Mikellidou, K., & Burr, D. C. (2018). The functional role of serial dependence.(1890). http://doi.org/10.1098/rspb.2018.1722

Collins, T. (2022a). Serial dependence occurs at the level of both features and integrated object representations.,(8), 1821−1832. http://doi.org/10.1037/xge0001159

Collins, T. (2022b). Serial dependence tracks objects and scenes in parallel and independently.,(7), 4. http://doi.org/10.1167/jov.22.7.4

Cremers, J. (2021).(2.0.2) [Computer software]. https://cran.r-project.org/web/packages/bpnreg/index.html

Cremers, J., & Klugkist, I. (2018). One direction? A tutorial for circular data analysis using R with examples in cognitive psychology.,2040. https://www.frontiersin.org/articles/10.3389/fpsyg.2018.02040

Dehaene, S. (2002). Précis of the number sense.(1), 16−36.

de Marco, D., & Cutini, S. (2020). Introducing CUSTOM: A customized, ultraprecise, standardization-oriented, multipurpose algorithm for generating nonsymbolic number stimuli.,(4), 1528−1537. http://doi. org/10.3758/s13428-019-01332-z

DeWind, N. K., Adams, G. K., Platt, M. L., & Brannon, E. M. (2015). Modeling the approximate number system to quantify the contribution of visual stimulus features.,, 247−265. http://doi.org/10.1016/j.cognition. 2015.05.016

Faul, F., Erdfelder, E., Buchner, A., & Lang, A. (2009). Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses.,(4), 1149−1160. http://doi.org/10.3758/BRM. 41.4.1149

Fischer, C., Czoschke, S., Peters, B., Rahm, B., Kaiser, J., & Bledowski, C. (2020). Context information supports serial dependence of multiple visual objects across memory episodes.,(1), 1932. http://doi.org/10.1038/s41467-020-15874-w

Fischer, J., & Whitney, D. (2014). Serial dependence in visual perception.,(5), 738−743. http:// doi.org/10.1038/nn.3689

Fisher, N. I. (1995).. Cambridge University Press.

Fisher, N. I., & Lee, A. J. (1992). Regression models for an angular response.,(3), 665−677. https://doi. org/10.2307/2532334

Flesch, T., Juechems, K., Dumbalska, T., Saxe, A., & Summerfield, C. (2022). Orthogonal representations for robust context-dependent task performance in brains and neural networks.,(7), 1258−1270. http://doi. org/10.1016/j.neuron.2022.01.005

Fornaciai, M., & Park, J. (2018a). Attractive serial dependence in the absence of an explicit task.,(3), 437−446. http://doi.org/10.1177/0956797617737385

Fornaciai, M., & Park, J. (2018b). Serial dependence in numerosity perception.,(9), 15. http://doi.org/10.1167/18.9.15

Fornaciai, M., & Park, J. (2019a). Serial dependence generalizes across different stimulus formats, but not different sensory modalities.,, 108−115. http://doi.org/10.1016/j.visres.2019.04.011

Fornaciai, M., & Park, J. (2019b). Spontaneous repulsive adaptation in the absence of attractive serial dependence.,(5), 21. http://doi.org/10.1167/19.5.21

Fornaciai, M., & Park, J. (2020). Attractive serial dependence between memorized stimuli.,, 104250. http://doi.org/10.1016/j.cognition.2020.104250

Fornaciai, M., Togoli, I., & Bueti, D. (2023). Perceptual history biases are predicted by early visual-evoked activity.(21), 3860−3875.

Franconeri, S. L., Bemis, D. K., & Alvarez, G. A. (2009). Number estimation relies on a set of segmented objects.,(1), 1−13. http://doi.org/10.1016/j.cognition. 2009.07.002

Fritsche, M., & de Lange, F. P. (2019). The role of feature-based attention in visual serial dependence.,(13), 21. http://doi.org/10.1167/19.13.21

Fritsche, M., Mostert, P., & de Lange, F. P. (2017). Opposite effects of recent history on perception and decision.,(4), 590−595. http://doi.org/10.1016/ j.cub.2017.01.006

Gekas, N., McDermott, K. C., & Mamassian, P. (2019). Disambiguating serial effects of multiple timescales.,(6), 24. http://doi.org/10.1167/19.6.24

Gross, H. J., Pahl, M., Si, A., Zhu, H., Tautz, J., & Zhang, S. (2009). Number-based visual generalisation in the honeybee.(1), e4263. https://doi.org/10.1371/ journal.pone.0004263

Harvey, B. M., Fracasso, A., Petridou, N., & Dumoulin, S. O. (2015). Topographic representations of object size and relationships with numerosity reveal generalized quantity processing in human parietal cortex.,(44), 13525−13530. http://doi.org/10.1073/pnas.1515414112

Kahneman, D., Treisman, A., & Gibbs, B. J. (1992). The reviewing of object files: Object-specific integration of information.,(2), 175−219. http:// doi.org/10.1016/0010-0285(92)90007-o

Kramer, A. F., & Jacobson, A. (1991). Perceptual organization and focused attention: The role of objects and proximity in visual processing.,(3), 267−284. http://doi.org/10.3758/bf03206750

Kutter, E. F., Bostroem, J., Elger, C. E., Mormann, F., & Nieder, A. (2018). Single neurons in the human brain encode numbers.,(3), 753−761.e4. https://doi. org/10.1016/j.neuron.2018.08.036

Kutter, E. F., Boström, J., Elger, C. E., Nieder, A., & Mormann, F. (2022). Neuronal codes for arithmetic rule processing in the human brain.,(6), 1275−1284. http://doi.org/10.1016/j.cub.2022.01.054

Lagona, F. (2016). Regression analysis of correlated circular data based on the multivariate von Mises distribution.,(1), 89−113. https://doi.org/10.1007/s10651-015-0330-y

Leibovich, T., Katzin, N., Harel, M., & Henik, A. (2017). From "sense of number" to "sense of magnitude": The role of continuous magnitudes in numerical cognition.,, e164. http://doi.org/ 10.1017/S0140525X16000960

Liberman, A., Fischer, J., & Whitney, D. (2014). Serial dependence in the perception of faces.,(21), 2569−2574. https://doi.org/10.1016/j.cub.2014.09. 025

Liberman, A., Manassi, M., & Whitney, D. (2018). Serial dependence promotes the stability of perceived emotional expression depending on face similarity.,(6), 1461−1473. http://doi. org/10.3758/s13414-018-1533-8

Liberman, A., Zhang, K., & Whitney, D. (2016). Serial dependence promotes object stability during occlusion.,(15), 16. http://doi.org/10.1167/16. 15.16

Lourenco, S. F., & Aulet, L. S. (2023). A theory of perceptual number encoding.,(1), 155−182. http://doi.org/10.1037/rev0000380

Manassi, M., Liberman, A., Kosovicheva, A., Zhang, K., & Whitney, D. (2018). Serial dependence in position occurs at the time of perception.,(6), 2245-2253. http://doi.org/10.3758/s13423-018-1454-5

Moon, J., & Kwon, O. (2022). Attractive and repulsive effects of sensory history concurrently shape visual perception.,(1), 247. http://doi.org/10.1186/s12915- 022-01444-7

Pascucci, D., Mancuso, G., Santandrea, E., Della Libera, C., Plomp, G., & Chelazzi, L. (2019). Laws of concatenated perception: Vision goes for novelty, decisions for perseverance.,(3), e3000144. http://doi. org/10.1371/journal.pbio.3000144

Pascucci, D., & Plomp, G. (2021). Serial dependence and representational momentum in single-trial perceptual decisions.,(1), 9910. http://doi.org/ 10.1038/s41598-021-89432-9

Pascucci, D., Tanrikulu, Ö. D., Ozkirli, A., Houborg, C., Ceylan, G., Zerr, P., Rafiei, M., & Kristjánsson, Á. (2023). Serial dependence in visual perception: A review.,(1), 9. https://doi.org/10.1167/jov.23.1.9

Pisa, P. E., & Agrillo, C. (2009). Quantity discrimination in felines: A preliminary investigation of the domestic cat (Felis silvestris catus).(2), 289−293. https://doi.org/10.1007/s10164-008-0121-0

Printzlau, F. A. B., Myers, N. E., Manohar, S. G., & Stokes, M. G. (2022). Neural reinstatement tracks spread of attention between object features in working memory.,(9), 1681−1701. http://doi.org/ 10.1162/jocn_a_01879

Ravindran, P., & Ghosh, S. K. (2011). Bayesian analysis of circular data using wrapped distributions.,(4), 547−561. https:// doi.org/10.1080/15598608.2011.10483731

Sadil, P., Cowell, R. A., & Huber, D. E. (2021). The push-pull of serial dependence effects: Attraction to the prior response and repulsion from the prior stimulus.https://doi.org/10.31234/osf.io/f52yz

Sadler, P. M., & Tai, R. H. (2007). The two high-school pillars supporting college science.(5837), 457−458.

Schwiedrzik, C. M., Ruff, C. C., Lazar, A., Leitner, F. C., Singer, W., & Melloni, L. (2014). Untangling perceptual memory: Hysteresis and adaptation map into separate cortical networks.,(5), 1152−1164. http://doi.org/10.1093/cercor/bhs396

Shan, J., & Postle, B. R. (2022). The influence of active removal from working memory on serial dependence.(1), 31. http://doi.org/10.5334/ joc.222

Starr, A., Libertus, M. E., & Brannon, E. M. (2013). Number sense in infancy predicts mathematical abilities in childhood.(45), 18116−18120.

Stern, Y., Ben-Yehuda, I., Koren, D., Zaidel, A., & Salomon, R. (2022). The dynamic boundaries of the Self: Serial dependence in the Sense of Agency.,, 109−121. http://doi.org/10.1016/j.cortex.2022.03.015

Suárez-Pinilla, M., Seth, A. K., & Roseboom, W. (2018). Serial dependence in the perception of visual variance.,(7), 4. http://doi.org/10.1167/18.7.4

Sun, Q., Zhang, H., Alais, D., & Li, L. (2020). Serial dependence and center bias in heading perception from optic flow.,(10), 1. https://doi.org/ 10.1167/jov.20.10.1

Togoli, I., Fedele, M., Fornaciai, M., & Bueti, D. (2021). Serial dependence in time and numerosity perception is dimension-specific.,(5), 6. http:// doi.org/10.1167/jov.21.5.6

Tokita, M., & Ishiguchi, A. (2010). How might the discrepancy in the effects of perceptual variables on numerosity judgment be reconciled?,(7), 1839−1853. http://doi.org/10. 3758/APP.72.7.1839

van der Burg, E., Rhodes, G., & Alais, D. (2019). Positive sequential dependency for face attractiveness perception.,(12), 6. http://doi.org/10.1167/19.12.6

Xia, Y., Leib, A. Y., & Whitney, D. (2016). Serial dependence in the perception of attractiveness.,(15), 28. http://doi.org/10.1167/16.15.28

Xu, L. H., Sun, Q., Zhang, B., & Li, X. (2022). Attractive serial dependence in heading perception from optic flow occurs at the perceptual and postperceptual stages.,(12), 11. https://doi.org/10.1167/jov.22.12.11

Yang, W. X., Zhang, M. L., Li, H. X., Yang, Y. L., & Si, J. W. (2017). Evolutionary evidences of primitive mathematics ability in human beings.(5), 810−824.

[杨伟星, 张明亮, 李红霞, 杨雅琳, 司继伟. (2017). 人类基本数学能力的进化证据.(5), 810−824.]

Zhang, H., & Luo, H. (2023). Feature-specific reactivations of past information shift current neural encoding thereby mediating serial bias behaviors.,(3), e3002056. http://doi.org/10.1371/journal.pbio.3002056

Zhou, J., Zhang, H., Ding, X., Shui, R., & Shen, M. (2016). Object formation in visual working memory: Evidence from object-based attention.,, 95−101. http:// doi.org/10.1016/j.cognition.2016.04.009

The effect of task relevance on serial dependence in numerosity

LIU Yujie1,2, LIU Chenmiao3, ZHOU Liqin3, ZHOU Ke3

(1State Key Laboratory of Brain and Cognitive Science, Institute of Biophysics, Chinese Academy of Sciences, Beijing 100101, China)(2Sino-Danish College, University of Chinese Academy of Sciences, Beijing 100049, China) (3Beijing Key Laboratory of Applied Experimental Psychology, National Demonstration Center for Experimental Psychology Education (Beijing Normal University), Faculty of Psychology, Beijing Normal University, Beijing 100875, China)

Serial dependence refers to the phenomenon where current perception is influenced not only by the current stimulus input but also by preceding events in recent history. This effect plays a crucial role in the establishment of relatively stable perceptions in dynamically changing environments. Previous studies have shown that the extent and direction of serial dependence are related to the task relevance of stimulus features. It is still unclear, though, if task relevance in linearly distributed features affects this impact, given that the majority of these researches have mostly focused on experiments using circularly distributed features. The current study investigated the impact of task relevance of linearly distributed features on serial dependence by using estimation tasks with dot arrays as stimulus materials, which were varying orthogonally in two dimensions: number/area (Experiment 1) or number/size (Experiment 2).

The study employed a 7 (number of dots) × 7 (dot array area in Exp 1/average dot size in Exp 2) × 2 (task relevance: relevant vs. irrelevant feature) block design. In the number estimation task, participants were instructed to focus on the number of dots, thus prioritizing the number as a relevant feature, while deeming the field area irrelevant. Conversely, the field area estimation task directed attention to the field area of dot array, making it the relevant feature and relegating the number to irrelevance. Experiment 2 followed the same experimental paradigm as Experiment 1, with the key difference being that it replaced the field area estimation task with an average item size estimation task. Each participant underwent all experimental conditions, with the order of the two tasks balanced across them. Initially, a fixation cross was presented for 1350−1450 ms, followed by a dot array image shown at the center of the screen for 250 ms. Task instruction then appeared at the top of the screen, accompanied by an axis beneath. Participants were instructed to accurately estimate the number of dots in the array by selecting a point on the number line through mouse click. The mouse click would trigger the appearance of a white marker, indicating the selected position, and its corresponding numerical value was exhibited underneath. Participants then affirm their estimation by pressing the “Enter” key. A response window of 15 seconds was provided; failure to respond within this period led to a 'no response' recording (marked as “N/A”) for that trial, and the program automatically proceeded to the next trial.

Our findings revealed that the effect of a feature from previous trial on current perception consistently counteracted the influence of the same feature in the current trial, regardless of the feature's task relevance. From a serial dependence perspective, the effects of previous task-relevant features were always repulsive; however, whether the previous task-irrelevant features showed attractive or repulsive serial dependence effects, was depended on the specific feature. This highlights the dual influence of task relevance and feature characteristics on the serial dependence effect of linearly distributed features. Notably, the persistence of the serial dependence of the irrelevant features implies that serial dependence can also arise at the object level.

serial dependence, numerosity perception, task relevance, linear distributed feature

2023-03-28

* 科技创新2030-重大项目(2021ZD0203803); 国家自然科学基金(32200840); 国家重点研发计划(2019YFA0709503); 中国博士后科学基金(2022T150061、2022M710435); 中央高校基本科研业务费支持。

周可, E-mail: kzhou@bnu.edu.cn; 周丽琴, E-mail: zhouliqin@bnu.edu.cn

B842