基于阶梯碳价和自适应分时电价的电动汽车有序充电

王 均，黄钶然，许 潇，吴 兰，姜 伟，黄明山

（1.河南工业大学 电气工程学院，河南 郑州 450001；2.四川大学 电气工程学院，四川 成都 610065；3.河南工业大学 机电工程学院，河南 郑州 450001；4.河南许继仪表有限公司，河南 许昌 461000）

0 引言

随着化石资源枯竭和环境问题的日益加剧，电动汽车受到了广泛的关注。纯电动汽车作为新能源汽车的代表，具有行驶成本低、温室气体排放少、能源多样化等优点。在新型电力系统“双高”“双峰”形势下，电动汽车和电网的双向能量交互可以促进电网削峰填谷和清洁能源消纳，实现电动汽车与能源互联网的融合发展［1］。然而，大量电动汽车的无序充电会引发电网峰值负荷陡增，影响电能质量，给配电网带来诸多挑战［2］。因此，确保电动汽车安全、可靠、经济运行是目前亟待解决的问题。

利用峰谷分时电价、实时电价和需求响应引导电动汽车用户合理充电，可以有效降低负荷峰谷差，提高电动汽车的充电效益。文献［3］提出了代理商和用户收益最大化的电动汽车有序充放电合作博弈模型，采用改进型分配原则对合作联盟收益进行公平分摊，并验证了基于动态分时交易电价的有序充电模型可以有效降低电网负荷的波动、提高联盟收益的稳定性。文献［4］提出了孤岛式光储充电站和电动汽车非合作Stackelberg 博弈的双层调度模型，通过实时电价引导电动汽车有序充电，实现了充电站收益的最大化。文献［5］建立了考虑电网公司、充电站运营商、电动汽车多方需求和决策特性的电动汽车有序充电模型，通过电价调节代价机制对充电站运营商进行补贴，保证了多方的盈利能力和配电网的运行安全性。文献［6］考虑“夜间充电、日间补贴”模式，提出了一种调控电动公交车有序充电的需求响应方法，通过削峰响应分段激励结算机制有效降低了电动公交车站的馈线负载率。然而，上述研究未将碳交易机制考虑到电动汽车的有序充电调度中。

2020 年，我国提出了碳达峰和碳中和的宏伟目标，许多学者围绕碳交易机制开展了相关的研究［7］。文献［8］针对综合能源系统提出了一种奖惩阶梯型碳交易模型，通过算例验证了所提模型对碳排放量的控制更加严格。文献［9］建立了电动汽车的碳配额模型，采用多目标粒子群优化算法进行求解，仿真结果验证了在引入电动汽车碳配额后，电动汽车的绿色性能得到充分发挥，但未将阶梯碳价与电动汽车的调度进行关联。因此，亟需提出一种综合考虑碳交易价格和动态分时电价的电动汽车有序充电定价策略，以解决新型电力市场中多主体的盈利能力评估和成本分摊问题。逼近理想解排序（technique for order preference by similarity to an ideal solu⁃tion，TOPSIS）模型可以快速高效地进行多主体、多目标综合评价，对评价对象进行优劣排序［10］。文献［11］提出了兼顾充电满意度和居民用电总负荷平稳性的多目标模型，采用TOPSIS 算法确定用户的充电排序优先级，通过电动汽车有序充电实现了电网和用户经济效益的双赢。为了解决电网规划中的多目标优化问题，文献［12］采用带精英策略的快速非支配排序遗传算法（fast and elitist non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ）求解风电场与电网联合规划多目标模型，通过TOPSIS 算法对Pareto 解集进行评分，进而确定风电场与电网联合规划的最优解推荐方案。

综上可知，现有的电动汽车有序充电策略未考虑碳交易价格和分时电价的内在耦合关联，为此本文提出了一种基于奖惩式阶梯碳价和自适应分时电价的电动汽车有序充电调度策略，并对碳交易机制的关键参数进行了灵敏度分析。在电碳双定价的基础上，构建了电网、电动汽车用户、发电商的多目标优化调度模型，采用熵权TOPSIS 模型对4 种碳交易机制下基于NSGA-Ⅱ得到的Pareto 解集进行评分排序，并输出各目标函数的权重。通过阶梯碳价和电网负荷的变化来激励动态分时电价，引导电动汽车用户有序充电，降低电网负荷波动，减少电动汽车用户的充电成本和发电商的碳交易成本。最后，通过算例分析和多场景对比，验证了所提策略的有效性和可行性。

1 电动汽车的无序充电模型

电动汽车的充电负荷模型主要取决于用户的返回时刻、日行驶里程等因素［13］。根据2009 年美国国家公路交通安全管理局的车辆出行统计数据［14］，电动汽车用户的返回时刻τ服从期望为μτ、标准差为στ的正态分布，其概率密度函数f(τ)为：

式中：μτ=17.6；στ=3.4。

电动汽车的日行驶里程d服从期望为μd、标准差为σd的对数正态分布，其概率密度函数f(d)为：

式中：μd=3.2；σd=0.88。

则电动汽车所需充电时长Tc可表示为：

式中：E为电动汽车的单位行驶行程耗电量，单位为kW·h／km；Pc为电动汽车的充电功率，单位为kW；ηc为电动汽车的充电效率。

利用蒙特卡罗方法生成电动汽车的无序充电场景，具体流程图见附录A 图A1。假设电动汽车在每天出行结束后立即以恒定功率进行充电，直到电动汽车的荷电状态（state of charge，SOC）达到设定值。电动汽车采用慢充模式，且假设充电期间不受分时电价的影响，充电功率Pc=3 kW，充电效率ηc=0.9，单位行驶行程耗电量E=0.195 kW·h／km［14］。通过单辆电动汽车充电功率的时序累加可计算得到电动汽车集群的总充电功率。附录A图A2展示了1 000辆电动汽车的无序充电负荷曲线。

2 奖惩式阶梯碳价和自适应分时电价模型

建立碳交易机制是为了实现节能减排的目标，通过合理分配或交易碳排放权，以此减少碳排放量［15］。我国的碳配额分配方式主要有无偿分配和有偿分配2 种。目前，我国电力行业主要采用无偿分配方式进行初始碳排放额的分配。本文假设所有电网负荷由煤电机组进行供电，并采用基准线法确定机组的无偿碳配额。

煤电机组每天的平均碳配额QH，av可表示为：

式中：PM，t为t时段煤电机组的有功出力，单位为MW；δH为煤电机组单位发电量的碳配额，本文中取值为0.798 t／（MW·h）［16］；Δt为单位时段时长；T为1 d的时段总数。

t时段煤电机组的实际碳排放量QF，t为：

式中：ζF为煤电机组的电力碳排放因子，表征每度电产生的碳排放量，取值为0.838 6 t／（MW·h）［17］。

2.1 奖惩式阶梯碳价模型

奖惩式阶梯碳价-碳交易量模型如附录A 图A3所示。当发电商的实际碳排放量大于无偿碳配额时，发电商在碳交易市场中购买超额碳排放权，从而保障煤电机组正常出力；当发电商的实际碳排放量小于无偿碳配额时，将盈余的碳排放额通过碳交易市场出售，以获取额外收益；当发电商的实际碳排放量等于无偿碳配额时，发电商无须购买或出售碳排放额。为了确保碳交易市场中碳价调度的灵敏性，设置5个购置碳排放量的正区间、2个出售碳排放量的负区间，根据实际碳排放量进行分段线性化。t时段的阶梯式碳交易成本CCO2，t为：

式中：Qt为t时段的碳排放权交易额，单位为t；L1、L0分别为碳排放量的正、负区间长度，单位为t；ξ1为奖励系数；λ1为碳交易基价，单位为元／t；τ1为碳交易成本增长率。

2.2 基于阶梯碳价的自适应分时电价模型

自适应分时电价随电网总负荷、碳交易价格动态变化，以实现电动汽车充电的全局调控。引入电价增长系数a1和电价下降系数b1，将初始电价与碳交易基价进行关联。将电价变化区间划分为上升区间和下降区间，可以灵活有效地对电动汽车进行调度。t时段自适应分时电价Xt的表达式为：

式中：Pav为电网的日负荷平均值，单位为MW；Xt0为碳交易机制下的初始电价，单位为元／（kW·h）；Y0为电价下降区间的设定功率，单位为MW；Y1为电价上升区间的设定功率，单位为MW；X0为无碳交易机制时的初始电价，本文中取值为0.944元／（kW·h）；λ0为初始碳交易基价，本文中取值为295 元／t；a0、b0分别为初始电价的增长、下降系数；τ0为初始碳交易成本增长率，本文中取值为0.3；ξ0为初始奖励系数，本文中取值为0.2；Pt0为不含电动汽车负荷的t时段电网原始负荷，单位为MW；PEV，t为t时段的电动汽车负荷，单位为MW；Pmax、Pmin分别为电网日负荷的最大值、最小值，单位为MW。

由式（8）—（11）可知，碳交易机制下的自适应分时电价与传统电价模型关联紧密。当碳交易基价λ1发生变化时，碳交易机制下的初始电价Xt0会随之变化。碳交易成本增长率τ1会影响峰时电价，奖惩式阶梯碳价模型中的奖励系数ξ1会影响谷时电价。式（6）—（16）将奖惩式阶梯碳交易机制与动态分时电价相关联，构建了基于阶梯碳价的自适应分时电价模型。

3 电动汽车的有序充电调度模型

3.1 电动汽车用户的价格响应模型

电动汽车用户的充电行为随着充电电价的变化而变化，充电行为的变化包括接受当前价格或改变充电时间。本文仅考虑电价对电动汽车用户充电行为的影响，忽略其他因素。电价综合反应函数为［18］：

式中：ρ(Xt)为电动汽车充电电量的变化率。

3.2 目标函数

为了验证所提模型的有效性，综合考虑电网、电动汽车用户和发电商的利益，构建多目标函数。

1）电网日负荷均方差最小。

减小负荷峰谷差对电网安全稳定运行至关重要，负荷越平稳，电网所受冲击越小。为了平抑电网的总负荷波动，以电网原始负荷与电动汽车充电负荷叠加后的负荷均方差最小为优化目标：

式中：F1为电网原始负荷与电动汽车负荷叠加后的负荷均方差，单位为MW2；为通过自适应分时电价调度后电网总负荷的平均值，单位为MW。

2）电动汽车用户的充电总成本最小。

电动汽车充电用户参与调度可以降低充电成本，为了保证用户的充电满意度，以电动汽车用户的充电总成本最小为优化目标：

式中：F2为电动汽车用户的充电总成本，单位为元。

3）发电商的碳交易成本最小。

煤电机组在发电过程中会产生碳排放量，为了提高发电商参加调度的积极性及保障其利益，以发电商的碳交易成本最小为优化目标：

式中：F3为发电商的碳交易成本，单位为元。

为了求解多目标函数解集的最优折中解，采用熵权TOPSIS 模型对式（18）—（20）中的3 个目标函数进行权重分配。分配权重后的多目标函数F为：

式中：ω1、ω2、ω3为熵权TOPSIS 模型分配的各目标函数权重，满足ω1+ω2+ω3=1；Fr，1、Fr，2、Fr，3为经过正向化、标准化后的各目标函数值。

3.3 约束条件

1）为了保证电动汽车能够正常行驶，即任意时段电动汽车电池的SOC 不能超过电池SOC 的上、下限，即：

式 中：SSOC，t为t时段电动汽车电池的SOC；SSOC，max、SSOC，min分别为电池SOC的上、下限。

2）从电网公司盈利与电动汽车用户节约成本两方面考虑，自适应分时电价应设置电价上限，且不应低于边际成本电价，即：

式中：Xmin、Xmax分别为边际成本电价、最高电价，本文中取值分别为0.25、3.00元／（kW·h）。

3）假设所有负荷均由煤电机组供电，则需满足如下功率平衡约束：

式（21）涉及电网、电动汽车用户、发电商多主体之间的联合优化，本文采用NSGA-Ⅱ求解多目标函数的Pareto 解集［19］。然后，利用熵权TOPSIS 模型对Pareto 解集进行正向化、标准化，计算各目标函数的权重，并输出经过评分排序后Pareto 解集的最优折中解［20］。熵权TOPSIS 模型的具体公式见附录A 式（A1）—（A10）。基于NSGA-Ⅱ和熵权TOPSIS 模型的多目标优化问题的求解流程图如图1所示。

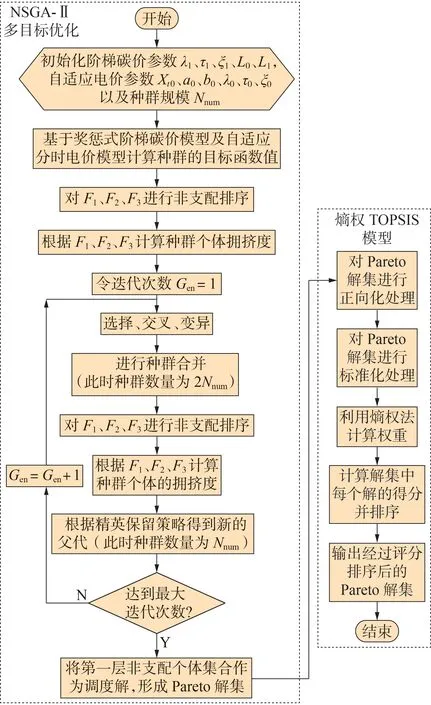
图1 多目标优化问题的求解流程图Fig.1 Flowchart of solving multi-objective optimization problem

4 算例分析

为了验证本文所提电碳双定价调控策略下电动汽车有序充电调度的有效性和经济性，以郑州市某10 kV馈线供电区域的日负荷曲线作为基础数据，假设辖区内有10 座大型商用充电站，每座充电站的最大充电功率为8.5 MW。电动汽车无序充电负荷和电网负荷功率曲线见附录A 图A4。电动汽车无序充电对电网运行造成了较大的冲击，在19:00时出现了“峰上加峰”的现象，电网最大负荷为478.5 MW。

将1 d等分为24个时段，选取4种不同的碳交易机制进行电动汽车有序充电建模仿真。碳交易基价λ1=335 元／t，碳排放量正区间长度L1=30 t，碳排放量负区间长度L0=40 t，初始电价增长系数a0=0.267 7，初始电价下降系数b0=0.093 9，碳交易成本增长率τ1=0.4，奖励系数ξ1=0.3。3 个目标函数权重分别为ω1=0.352、ω2=0.241、ω3=0.407。

4.1 4种碳交易机制的调度结果对比分析

为了验证不同碳交易机制对电网、电动汽车用户以及发电商的影响，设置4 种场景进行对比分析：①场景1，考虑奖惩式阶梯碳价机制的电动汽车充电调度；②场景2，仅考虑无奖励阶梯碳价机制的电动汽车充电调度；③场景3，考虑均碳价且无奖励机制的电动汽车充电调度；④场景4，无碳交易机制的电动汽车充电调度。

4 种场景下电动汽车参与电网负荷削峰填谷的效果见图2。4 种场景下电网日负荷均方差、电动汽车用户的充电总成本、发电商的碳交易成本及评分结果见表1。可以看出：相较于场景2 — 4，场景1 的日负荷均方差分别下降了39.09 %、47.99 %、32.19 %；相较于场景1、3、4，场景2的电动汽车用户充电总成本分别减少了49.64 %、42.50 %、73.23%；场景1的电动汽车用户的充电总成本相较于场景4 减少了46.84 %，发电商的碳交易成本相较于场景2、3 分别减少了88.49 %、90.55 %；相较于场景2 — 4，场景1考虑了奖惩式阶梯碳价和自适应分时电价策略，对电动汽车有序充电调度及电网削峰填谷的效果最为显著。

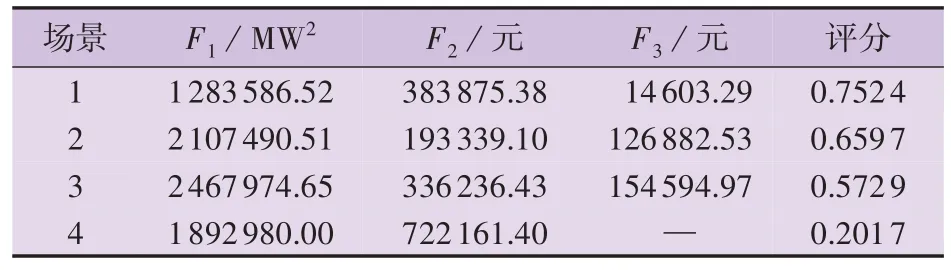
表1 4种场景的调度结果对比Table 1 Comparison of scheduling results among four scenarios

图2 4种场景下的电网总负荷对比Fig.2 Comparison of total grid load under four scenarios

4 种碳交易机制对3 个目标函数的影响呈现较大的差异，具体对比分析如下。

受自然和人类工程活动的综合作用，乐山市境内地质灾害种类发育较齐全、数量多，但分布不均，且具突发性及不可预见性。地质灾害种类以滑坡、崩塌(危岩)为主，其次为潜在不稳定斜坡、泥石流、地面塌陷(地面裂缝)。其中滑坡约占50%，崩塌约占30%，潜在不稳定斜坡、泥石流、地面塌陷、地裂缝等地质灾害约占20%。

1）4种场景的电网日负荷均方差对比。

场景1 考虑了奖惩式阶梯碳价和自适应分时电价策略，碳价对电价的调整作用比较明显，电网日负荷均方差大幅度减小，即电网总负荷曲线更加平滑。场景2和场景3采用不同的碳交易机制，当实际碳排放量低于无偿碳配额时，碳价、电价均未发生变化，电网负荷谷时段未调整。场景4 在无碳交易机制下对谷时段负荷进行正常调度，使得场景4 的电网日负荷均方差均比场景2、3 小。场景4 未考虑碳价的影响，电网负荷调整仅与电价相关，其调度效果与场景1有所差异。

2）场景1 — 3 中电动汽车用户的充电总成本对比。

场景1 中的自适应分时电价在奖惩式阶梯碳价的影响下会对电动汽车用户的充电行为产生调整作用，引导更多的用户在电网负荷谷时段充电，使得电网总负荷曲线在谷时段明显上升。在场景2、3 的碳交易机制下，发电商在电网负荷谷时段无法通过出售盈余的碳排放额获利，使得电价未跟随碳价变化，因此场景2、3 下谷时段的负荷曲线保持不变，电网总负荷曲线仅在峰时段下降。场景1、2 的碳交易机制仅在电网负荷谷时段有所差异，且奖惩式碳交易机制会引导更多的电动汽车用户在谷时段充电，使得场景1的电动汽车用户充电总成本比场景2大。

3）场景1 — 3中发电商碳交易成本对比。

场景1 考虑了奖惩式阶梯碳价机制，当实际碳排放量低于无偿碳配额时，发电商会将盈余的碳排放额出售以获利。场景2、3 下，发电商无碳配额出售权限，故其碳交易成本比场景1高。场景3采用均碳价机制，单位碳排放量价格保持不变，使得碳价对电价、电网负荷的调节作用较弱，因此场景3 中电网峰时段的总负荷功率比场景2 高。场景2、3 所用碳交易机制的区别在于：当实际碳排放量大于无偿碳配额时，场景2 的碳价阶梯上升，而场景3 的碳价未发生变化。因此，场景2 的碳交易机制对电网峰时段负荷的削峰效果更显著，使得场景3 的发电商碳交易成本比场景2高。

4.2 奖惩式阶梯碳价对电动汽车调度的影响

采用熵权TOPSIS模型对4种碳交易机制下的调度结果进行综合评价，由表1 中的评分可知：考虑奖惩式阶梯碳价机制对电动汽车的有序充电调度、电网负荷削峰填谷效果最好，评分值最高，为0.752 4。场景1 所用碳交易机制下多目标函数的Pareto 前沿如图3 所示。由图可知：减少发电商碳交易成本或电动汽车用户充电成本会使电网日负荷均方差变大。场景1 考虑了奖励机制，当实际碳排放量小于无偿碳配额时，发电商会将盈余的碳排放额通过碳交易市场出售以获利，使得发电商碳交易成本为负值。

4.3 奖惩式碳交易机制下关键参数的灵敏度分析

碳交易机制下关键参数的选取会直接影响分时电价，通过灵活调整关键参数取值可以实现电动汽车用户充电行为的差异化调控。为此，本节着重讨论场景1 中的碳排放量正区间长度L1、碳交易成本增长率τ1、碳交易基价λ1、奖励系数ξ1对电动汽车参与电网调度的影响，结果分别如附录A图A5 — A8所示。由附录A 式（A1）和式（A2）可知：经正向化、标准化处理后的目标函数值Fr，1、Fr，2、Fr，3越大，表明对应的目标函数F1、F2、F3越小。

由图A6可知：当发电商的实际碳排放量大于无偿碳配额时，随着碳交易成本增长率τ1增大，阶梯式碳交易成本CCO2，t随之增大。高电价抑制了电动汽车用户的充电需求，导致其选择在电价谷时段进行充电，此时Fr，1、Fr，2、Fr，3逐渐增大。

由图A7可知：当碳交易基价λ1在255～275元／t内变化时，随着λ1增大，Fr，1逐渐增大；当λ1在275～335 元／t 内变化时，随着λ1增大，碳价对电价的调控作用增强，峰时段电网负荷减小。因为初始电价Xt0受λ1的影响较大，导致谷时段电动汽车用户的充电积极性不高，相较于λ1=275 元／t，当λ1在295～335元／t内变化时，谷时段负荷的抬升效果减弱，使得电网日负荷均方差较大。当λ1逐渐增大时，电动汽车用户避峰充电，使得碳排放量处于高梯度的时间减少，电动汽车用户的充电成本逐渐减小。同时，发电商碳交易成本处在低碳价的时间较长，Fr，3逐渐增大。

当发电商的实际碳排放量小于无偿碳配额时，其可以在碳交易市场出售盈余碳排放额以获得一定的奖励，此时奖励系数ξ1会影响电网谷时段负荷的变化。由图A8 可知：当ξ1增大时，发电商收益逐渐增加，谷时段电价的下降幅度增大，促使电动汽车用户在电网负荷谷时段充电，从而使电动汽车用户的充电成本增大；同时，电网谷时段负荷曲线抬升，使得Fr，1增大；随着ξ1增大，碳价对电价的影响增大，电动汽车用户集中在电网负荷谷时段充电，发电商煤电机组的碳排放量随之增大，碳交易成本升高，使得Fr，3减小。

为了分析上述4 个关键参数对电网总负荷峰谷差的影响，分别对各参数调控下的电网总负荷进行对比，如图4 所示。场景1 考虑了奖惩式碳交易机制，关键参数取值为L1=30 t、τ1=0.4、λ1=335 元／t、ξ1=0.3。采用熵权TOPSIS 模型进行评估，以获得最高评分。可见：通过在电碳双定价机制下合理设置关键参数取值，可以有效引导电动汽车有序充电，促进电力需求侧移峰填谷，降低发电商的碳交易成本。

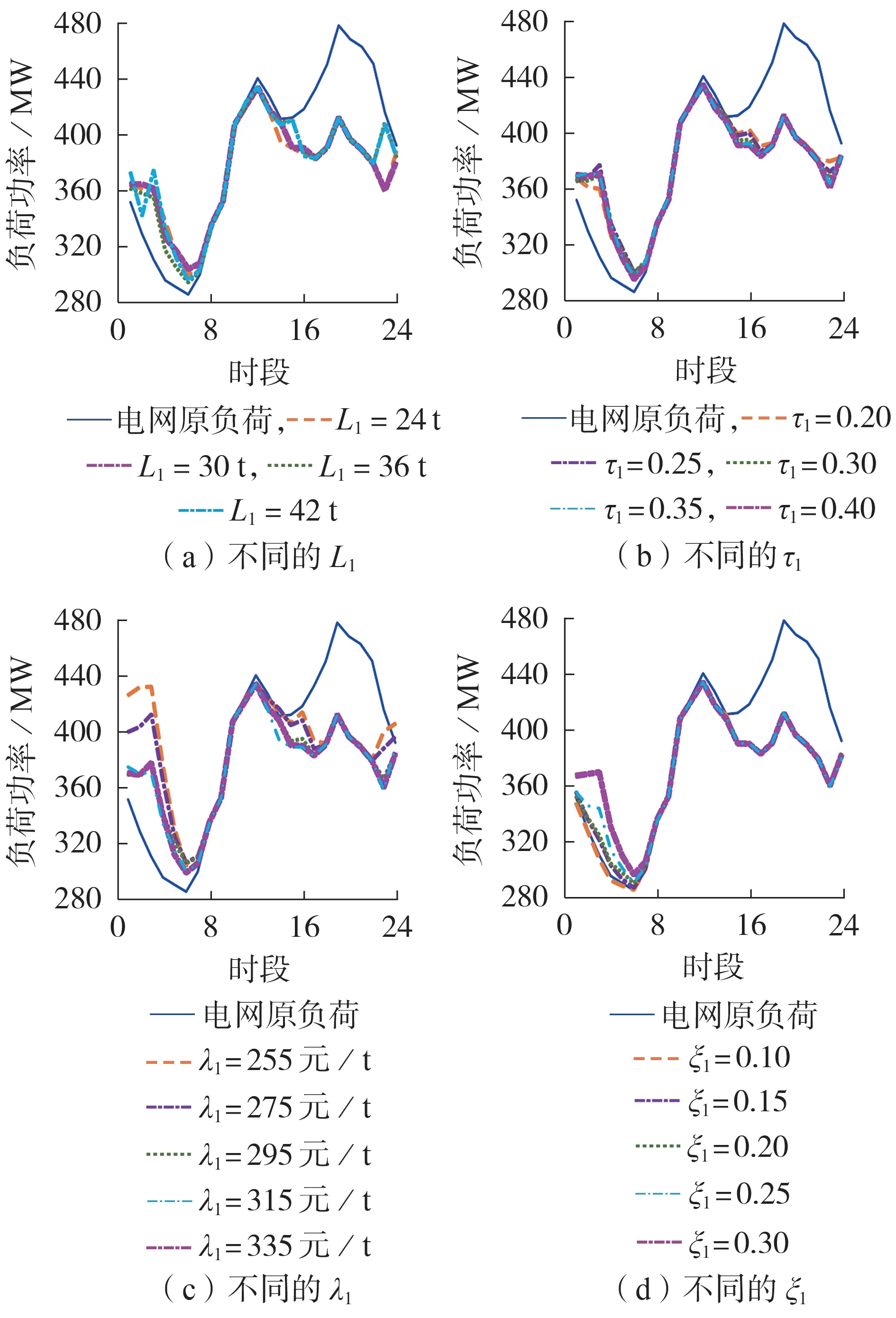
图4 关键参数取值对电网总负荷的影响Fig.4 Influence of values of key parameters on power grid total load

5 结论

本文提出了一种基于电碳双定价机制的电动汽车有序充电策略，利用蒙特卡罗方法生成电动汽车的无序充电场景，并分别建立奖惩式阶梯碳价和自适应分时电价模型，采用熵权TOPSIS 模型对NSGA-Ⅱ求得的多目标函数Pareto 解集进行正向化、标准化，输出各目标函数的权重，根据评分排序后得到最优折中解。通过对比4 种不同的碳交易机制下电动汽车用户充电行为的变化以及对碳交易关键参数的灵敏度分析，得到以下结论：

1）与无奖励、均碳价和无碳交易机制相比，奖惩式阶梯碳价和自适应分时电价机制对电动汽车有序充电的优化调度效果最佳，可以有效降低发电商碳交易成本，促进电网总负荷削峰填谷，实现电网、电动汽车用户和发电商的利益共赢；

2）对比奖惩式碳交易机制中4 个关键参数不同取值对电动汽车参与电网调度运行的影响，结果表明通过灵活选取碳交易机制下关键参数的取值，可以实现对电动汽车用户充电行为的差异化调控。

本文仅考虑了电网侧对电动汽车有序充电的影响，未计及交通信息影响下电动汽车充电负荷接入电网的时空分布特性，未来会进一步考虑电力-交通耦合网络下基于出行链理论刻画电动汽车出行空间特征的分层定价方法及有序充电策略。

附录见本刊网络版（http：//www.epae.cn）。