计及参与成本贡献的用户侧云储能服务及其纳什议价模型

谢涵铮，刘友波，马 超，殷 科，向 月，荆 渝，唐 早，刘俊勇

（1.四川大学 电气工程学院，四川 成都 610065；2.国网四川综合能源服务有限公司，四川 成都 610031；3.杭州电子科技大学 自动化学院，浙江 杭州 310038）

0 引言

储能作为一种能源灵活中转站，是未来以新能源为主体的新型电力系统中不可或缺的部分。 “双碳”目标下，我国新能源的并网率逐步提升［1］，用户侧分布式储能的应用也愈加普遍，电力用户从传统意义上的能源消费者逐步过渡为产消者。但受环境限制、价格约束、信息不对称等因素影响，且大多用户对储能设备缺乏有效的管理手段和精准的控制技术，储能的经济效益未能得到充分挖掘，用户难以获得可观的收益［2］。文献［3］提出了基于共享经济理念的新型储能商业模式——云储能（cloud energy storage，CES），云储能运营商（cloud energy storage operator，CESO）通过建设规模化储能，并对其进行集中式服务管理控制，可为用户提供可租赁的虚拟分布式储能服务。相较于分布式储能，集中式储能设备具有低边际投资及运行成本，同时结合运营商的优化控制手段，可使储能的经济效益得到充分体现，并为运营商提供利润空间。

近年来，国内外对共享储能的商业模式已有较完备的研究，不同类型模式下储能的从属关系、投资主体不同，故合理的服务定价或成本收益分配机制是亟需解决的问题之一。目前基于博弈论的定价机制是一主流方向，可分为非合作博弈和合作博弈2 种模式。非合作博弈中由于各主体间对资源或利益的竞争，储能共享的价值往往有所损失，具体可总结为：①储能需求者因使用的分散独立性及能量流动的闭塞性产生了多余的用能成本［4⁃5］；②储能提供者和需求者之间因利益冲突导致社会最优点的偏离［6］。因此，该模式始终存在可减小的社会成本。

合作博弈注重资源整合及能量协同，可以更低的成本实现储能的高效利用。如：文献［7］建立了分布式能源的共享机制，各设备共享后协同配合使得储能的利用率得到有效提升，但合作博弈下联盟内部效益分配的公平合理性是保证合作的前提［8］。文献［7］采用常规Shapley 值法对合作后的经济效益进行分配，但文献［9］对其弊端进行了分析，点明该方法只考虑了联盟中成员的边际贡献，而未计及其风险偏好，可能导致联盟解体。有研究对该方法进行了改进，如：文献［10］采用Shapley 值法对多微电网共享储能节省成本进行分摊，对线路功率损耗大的微电网适当增加节省成本，提升了其投资积极性；文献［11］采用核仁法为共享储能投资方分配成本，该方法以最小化联盟内部参与者的不满意度进行分配，结果较Shapley 值法稳定且唯一；文献［12］设计了计及主体参与度差异性的CES 纳什议价模型，为社区和用户分配CES 费用，纳什议价保证了各主体收益的帕累托最优，但所定义的参与度描述不够合理，缺乏对储能使用者因充放电需求互补对运行成本减少的实际贡献的考虑。因此，合作博弈模式下应设计更公平的贡献分配机制为参与者分配效益，以促使各主体合作共赢。

基于上述分析，本文提出了计及参与成本贡献的CES 纳什议价模型，对CESO 独立投资的集中式CES 服务进行定价。在所述框架中，CESO 优先对需求互补的用户交换电能，并仅需满足总体净充放电需求，从而可减小实体储能过多的充放电损耗及总体用能成本，并提升新能源的就地消纳。在贡献分配方面，采用Shapley 值法分配用户对储能的损耗贡献，以体现用户在联盟下因需求互补对储能损耗减少的影响，并综合考虑用户的新能源余量能量互济率和虚拟储能利用率对分配结果进行改进，以进一步促进用户的新能源余量上网及对虚拟储能的按需租赁；通过贡献度描述用户的服务费差异性，并设置统一的费用系数求解纳什议价模型，可在保证用户服务费差异合理的前提下，兼顾用户群体与CESO的利益诉求，最终实现成本和收益在各主体间的合理分配，促进各方合作。

1 CES服务框架

CES 服务框架如图1 所示，集中式实体储能由CESO 投资建设，与配电网连接，向用户提供虚拟储能租赁服务。储能的充放电功率、用户的新能源出力及负荷均由配电网传输，各主体的交互如下。

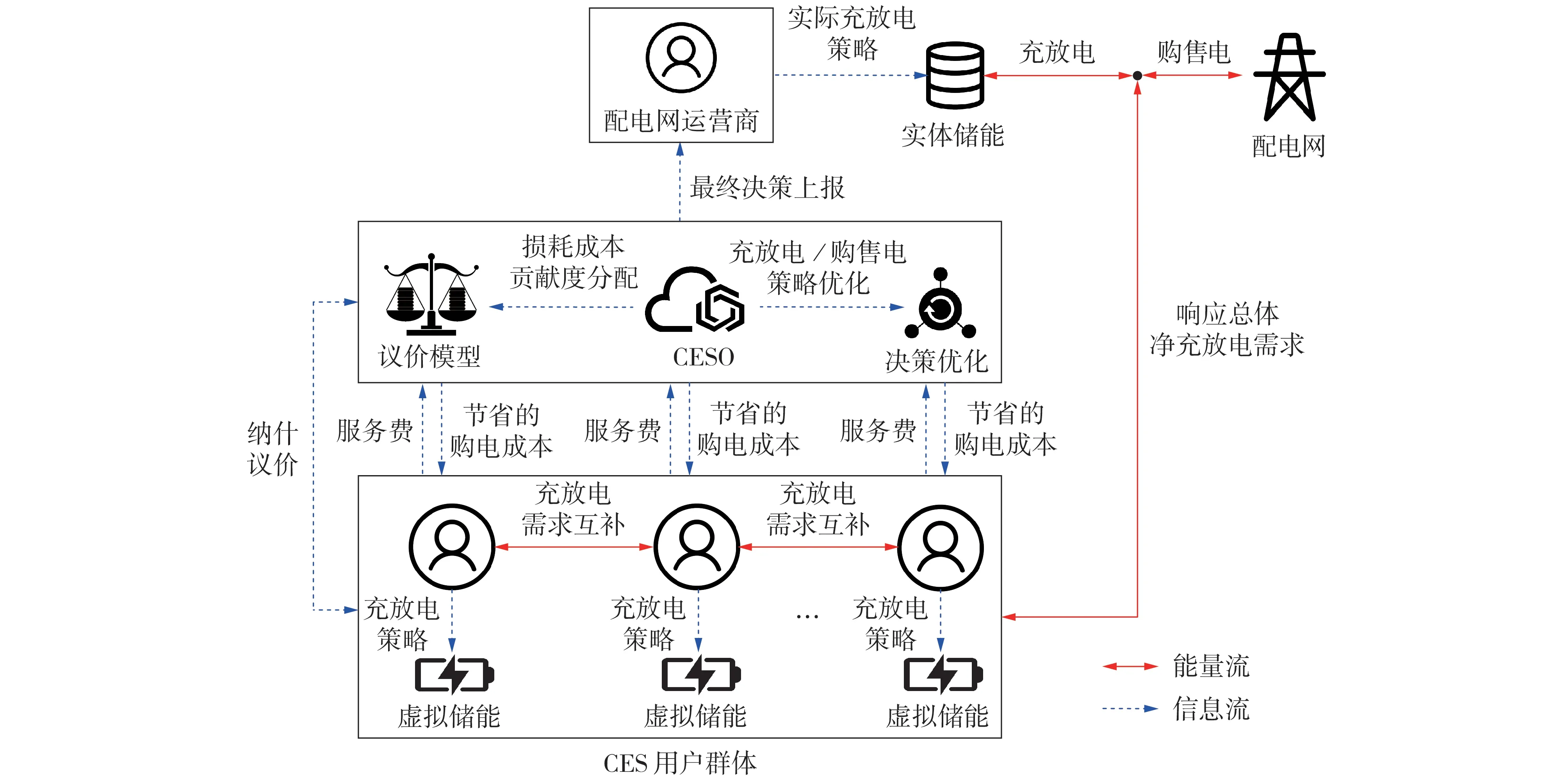
图1 CES服务框架Fig.1 Framework of CES service

1）用户i日前向CESO 申报租赁虚拟储能的额定容量ecapi及额定充电功率pc，capi、额定放电功率pd，capi，获得虚拟储能的使用权。结合次日负荷计划和新能源预测出力后，以购电成本最小化决策其次日的虚拟储能充放电策略，并将策略上报CESO。

2）CESO 将各用户虚拟储能的充放电策略叠加后，为了节省次日实体储能不必要的充放电损耗，并提升新能源的就地消纳率，对同一时段充放电需求互补的用户优先交换电能，因此CESO 仅需响应用户总体净充放电需求。对于交换后各时段的盈余或缺额电能，将由CESO 通过实体储能充放电或向电网购售电来满足，以达成各用户端口功率平衡。CESO 将以运行成本Cces最小化决策次日各时段实体储能的充放电功率和向电网的购售电功率，并将最终调度策略上报给配电网运营商，由其于次日执行调度方案。

3）当用户的虚拟储能租赁到期时，需向CESO支付服务费，服务费定价步骤如下：

a）计算CESO 的实体储能损耗成本Clossces及各用户因参与CES服务节省的购电成本Bi；

b）采用Shapley 值法为用户i分配实体储能损耗成本贡献度Ci，con，并综合考虑用户的新能源余量能量互济率及虚拟储能使用率，对Ci，con进行改进，最终通过改进后的贡献度C∗i，con刻画 各 用户的服务费差异性；

c）为用户群体设置统一的服务费系数η，以保证用户彼此服务费差异性的合理，并构建计及用户成本贡献的纳什议价模型，计算用户i的服务费，最终可兼顾用户群体和CESO的利益诉求。

2 CES运行模型

2.1 用户虚拟储能运行模型

2.1.1 目标函数

设定用户对虚拟储能的控制逻辑为：可通过虚拟储能充放电节省购电成本，但优先利用其新能源出力满足负荷，若存在过剩出力，则存入虚拟储能备用，并在购电电价高且存在负荷缺口的时段放出。基于此，用户虚拟储能运行模型的目标函数可表示为：

式中：C为用户i的购电成本为t时段电网的购电电价；p为t时段用户i从电网购电的功率；Δt为单位时段的时长；T为时段总数。

2.1.2 约束条件

用户配合其虚拟储能后需满足用电端口功率平衡约束，即：

式中：p、p分别为t时段用户i的负荷计划、新能源出力；p、p分别为t时段用户i虚拟储能的充、放电功率。

另外，还需满足虚拟储能的常规运行约束，具体见附录A式（A1）—（A6）。

2.2 CESO实体储能运行模型

2.2.1 目标函数

CESO 将以最小化运行成本Cces为优化目标，如式（3）所示。

式中：I为电网购售电收益；ε为储能单位充放电功率的损耗成本；P、P分别为t时段实体储能的充、放电功率；P、P分别为t时段CESO 向电网的购、售电功率；为t时段电网的售电电价。

2.2.2 约束条件

用户联盟需求互补后，CESO决策通过实体储能充放电或从电网购售电达成的各用户用电功率平衡约束如式（6）所示。用户联盟需求互补后的累计净充电功率应与实体储能的累计充电功率相等，如式（7）所示，该约束的意义在于响应用户总体净充放电需求后，CESO可能将剩余储能资源充放电用于购售电套利，这部分效益不属于提供CES 服务的运行成本部分。

式中：N为CES 用户数量；为用户联盟需求互补后的功率；[x]+的定义式如式（8）所示。

另外，还需满足实体储能的常规运行约束，具体见附录A式（A7）—（A13）。

3 CES服务定价

CESO作为实体储能的投资方，在提供虚拟储能租赁服务时会产生一定的成本，应向各用户收取租赁服务费以保证自身的利润空间。实际上，用户的服务费除受租赁规模、充放电情况等因素影响外，还与其所在的用户联盟相关。当各用户参与CES服务形成天然的合作联盟后，CESO因联盟内部需求互补使响应总体净充放电需求时储能的损耗成本减小，这也会对其服务费产生影响。为了合理刻画各用户CES服务费的差异性，并保证用户群体和CESO之间净收益分配均衡，本章提出了计及用户成本贡献的纳什议价模型，为CES服务定价。

CES服务定价流程如图2所示。首先，基于CES的运行模型求解双方的决策，计算各主体的成本及收益；然后，采用Shapley 值法为各用户分配其对实体储能损耗成本Clossces的贡献度，并综合考虑各用户的新能源余量能量互济率、虚拟储能利用率，对常规分配结果进行改进；最后，以改进后的结果刻画各用户服务费的差异性。同时，对用户群体设置统一的服务费系数η，在计及成本贡献的纳什议价模型中，对于损耗成本贡献度高的用户，其服务费也应更高，因此可在保证服务费差异性合理的前提下，使得用户与CESO 议价时彼此的效益公平分配，促进双方合作。

图2 CES服务定价流程Fig.2 Pricing process of CES service

3.1 各主体的成本及收益

3.1.1 CESO提供CES服务的成本

对于用户群体需求互补后的能量盈余，CESO将其于电价较高时段售出，并提前向电网购入低价电充入实体储能以套利；同理，CESO 可低价从电网购电以满足能量缺额，并将其本应放出的电能于电价较高时段放出以套利。CESO 仅需通过达成用户端口功率平衡为其提供名义上的充放电需求即可，因此其运行成本中的电网购售电收益I可完全为CESO 私有，故本文将实体储能的充放电损耗成本C作为CESO提供CES服务所产生的成本。

3.1.2 CES用户节省的购电成本

用户参与CES 服务后可节省购电成本，为其虚拟储能的放电收益与从电网购电以充电的成本之差，用户i节省的购电成本Bi可表示为：

式中：p为t时段用户i的虚拟储能充电功率中从电网购电的充电功率；p为t时段用户i过剩新能源充入其虚拟储能的功率；ei，t-1为t-1 时段用户i虚拟储能的容量；为用户i虚拟储能的充电效率。

3.2 基于改进Shapley 值法的实体储能损耗成本贡献度量化

3.2.1 常规Shapley值法下的损耗成本分配策略

各用户因虚拟储能使用情况、与其他用户充放电需求互补效果等因素的不同，对实体储能损耗成本的影响程度也不同，为了合理地衡量用户在大联盟下对损耗成本的贡献，可采用合作博弈领域中的Shapley 值法量化用户的贡献度，根据各用户对所在合作联盟的边际贡献率确定其贡献度。例如：用户i在参与合作联盟S时有(|S|-1)！种排序（|S|为合作联盟S中包含的CES 用户数量），剩余未参与合作联盟的N-|S|个用户有(N-|S|)！种排序，其参与的不同排序组合除以N个用户的排序组合即为合作联盟S分配成本的权重γS，即：

用户i参与不同联盟S创造的边际贡献Ci，S为：

因此，用户i的损耗成本贡献度Ci，con为：

式中：Sall={1，2，…，N}；C(S)为联盟S下实体储能的损耗成本；C(S{i})为联盟S中除去用户i后实体储能的损耗成本。

3.2.2 贡献度的改进因素

传统Shapley 值法只考虑了用户对合作联盟的边际贡献，未计及各用户自身风险分担因素，实际上隐含了各用户彼此风险分担均等的假设，为此本文考虑从以下2点对该方法的分配结果进行修正。

1）新能源的余量能量互济率。

对于将新能源的剩余出力充入虚拟储能的用户而言，其可与其他放电用户直接进行电能匹配，以减少实体储能因充放电产生的过多损耗，因此可对新能源余量能量就地消纳率高的用户减少一定的损耗成本贡献度。定义此时用户i的分摊系数Ki，comp为：

式中：pmp为t时段用户i的新能源余量互济量。

2）虚拟储能利用率。

为了激励用户按需租赁虚拟储能，充分利用储能资源，以减少CESO 初期对实体储能的投资成本，可根据用户的累计充放电功率占其虚拟储能容量的比例衡量用户的虚拟储能利用率，对利用率高的用户减少一定的损耗成本贡献度。定义此时用户i的分摊系数Ki，use为：

3.2.3 损耗成本贡献度的再分配

综合考虑新能源余量能量互济率和虚拟储能利用率后，用户i的再分摊系数Ki可表示为：

式中：α、β分别为分摊系数Ki，comp、Ki，use的权重值，可通过熵权法确定，即所含信息量大的分摊系数对应的权重值更大，且α+β=1。

改进后用户i的损耗成本贡献度C∗i，con可表示为：

式中：ΔKi为用户i损耗成本贡献度的调整系数；μ为控制系数，用于保证改进后大联盟内各用户的贡献度小于其单独参与CES服务后的贡献度。

3.3 基于纳什议价模型的CES服务费求解

3.3.1 计及参与成本贡献的CES服务议价模型

CES 服务中，用户的净收益为其节省的购电成本Bi与服务费之差，CESO的净收益为各用户的服务费总和与其实体储能的损耗成本之差，二者可通过议价提升彼此的利益。在合作博弈领域，纳什议价模型可保证博弈过程中各主体效益的帕累托最优，具有个体理性、独立性、对称性等特点，能有效引导存在利益冲突的主体之间的合作［13］，因此可通过纳什议价模型为CES服务进行定价。为了保证各用户之间服务费差异性的合理，各用户所缴纳的服务费应与其损耗成本贡献度Con成正比，因此可设定统一的服务费系数η，即用户i支付的CES 服务费qi应满足：

据此构建计及用户成本贡献的纳什议价模型，使用户群体和CESO 之间的净收益分配均衡。优化模型可表示为：

式中：R为各主体的效用函数乘积，(η-1)C为CESO的效用函数Bi-ηC)为用户群体的效用函数，为各用户参与CES服务的净收益乘积。CESO的谈判破裂点为其实体储能损耗成本C，各用户的谈判破裂点为其节省的购电成本Bi。

3.3.2 纳什议价问题的转换

纳什议价模型的优化目标为各主体效用函数的乘积，属于非凸非线性优化问题，可通过对目标函数取对数，将其转化为求解对数之和最大值的问题［14］，转换后的新目标函数R'为：

除去常量后按照参与合作的主体对新目标函数进行划分，第k次议价时CESO的目标函数为：

式中：Rces，k为第k次议价时CESO 的效用；ηces，k为第k次议价时CESO期望的服务费系数。

第k次议价时用户群体的目标函数为：

式中：Ruser，k为第k次议价时用户群体的效用；ηuser，k为第k次议价时用户群体期望的服务费系数。

按各主体划分目标函数之后，可以采用交替方向乘子法（alternating direction method of multipliers，ADMM）求解服务费系数η，该方法结合了对偶上升法的可分离特性及增广拉格朗日乘子法的松弛收敛条件，能求解有可拆分结构的凸优化问题［15］，具体求解步骤见第4章。

4 问题求解

本文采用商业求解器CPLEX 及ADMM 对优化模型进行求解，具体求解步骤如下：

1）各用户上报租赁的虚拟储能规模及期限；

2）根据用户虚拟储能和CESO 实体储能的运行模型求解CES服务中各主体的调度策略；

3）计算不同用户联盟下实体储能的损耗成本C(S)及各用户参与CES服务节省的购电成本Bi；

4）采用改进Shapley 值法为各用户分配损耗成本贡献度con；

5）构建计及用户成本贡献的纳什议价模型，求解服务费系数η，得到各用户的CES服务费。

ADMM 求解纳什议价模型的流程图见附录A 图A1，具体步骤如下。

1）设置初始CESO 和用户群体的服务费系数ηces，0、ηuser，0，初始化拉格朗日系数λ0、惩罚系数ρ，设定迭代阈值ε1、ε2。

2）求解CESO 优化服务费系数ηces，k问题，如式（26）所示，将其记为Q1。

3）求解用户优化服务费系数ηuser，k问题，如式（27）所示，将其记为Q2。

4）根据式（28）更新拉格朗日系数λk。

5）判断是否满足迭代终止判据，若满足，则终止迭代；否则，返回步骤2）继续迭代。

5 算例分析

5.1 算例参数

本文以3 个工业用户某典型日的数据［16］为算例进行仿真分析，其次日的负荷计划和新能源预测出力分别见附录A 图A2和图A3，其中用户1配备了光伏和风机，用户2和用户3配备了光伏。用户虚拟储能的规模按照文献［17］中的方法建立，并考虑用户因非理性决策导致的最优租赁规模存在一定的偏离，参数设定源自文献［18］。实体储能的规模设定为各用户租赁虚拟储能规模的总和，用户虚拟储能的充放电效率、荷电状态上下限与CESO 实体储能的参数一致。依据江苏省某年工业用户的峰谷分时电价时段对电价进行划分。具体参数见附录A 表A1 — A4。结算周期为1 d，储能单位电量的充放损耗成本为0.1元／（kW·h）［19］。

5.2 算例结果分析

5.2.1 各主体CES模型的运行情况分析

CESO 层面接收到的各时段用户群体虚拟储能的累加充放电功率如图3 所示（充电功率为正值，放电功率为负值），CESO 为了满足用户总体净充放电需求的实体储能充放电策略及购售电策略如图4 所示（购电功率为正值，售电功率为负值）。

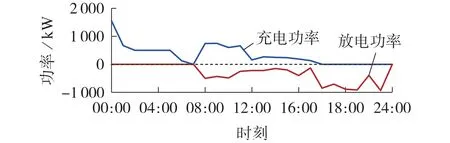
图3 用户群体虚拟储能的累加充放电功率Fig.3 Cumulative charging and discharging power of user community’s virtual energy storage

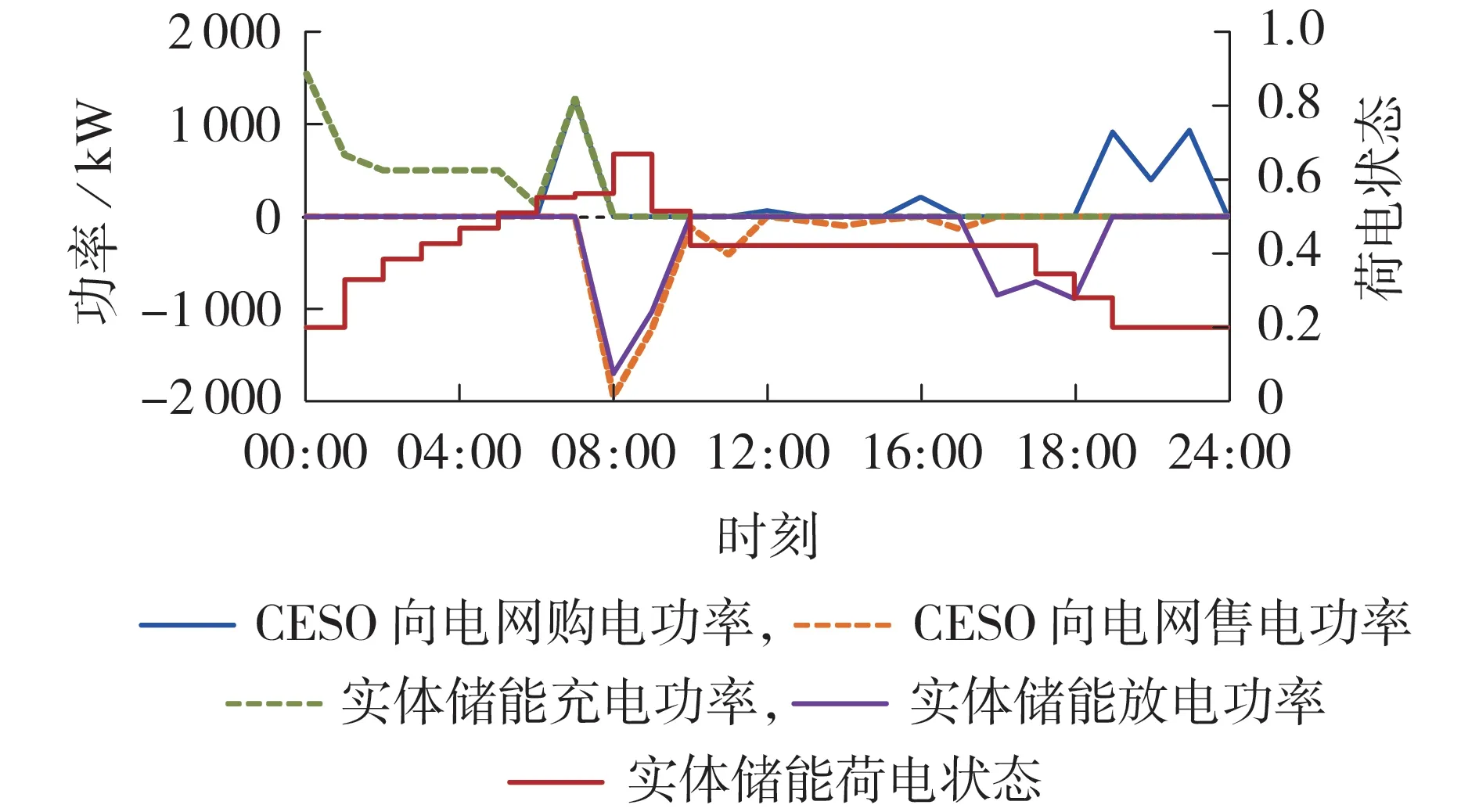
图4 CESO实体储能的充放电及购售电策略Fig.4 Charging／discharging and power purchasing／selling strategies of CESO’s physical energy storage

结合图3和图4可知：电价谷时段［00:00，08:00］，CESO 将用户群体的购电功率及用户1 的风电余量充入实体储能，并在［07:00，08:00］额外向电网购电，将之后时段内因用户需求互补售出的总能量盈余（1 276.431 kW）提前转移至电价低谷时段充入储能，由此获得充电套利收益；（08:00，18:00］时段包含电价峰平时段，因部分用户的新能源出力过剩，存在用户充放电需求互补的现象，CESO 对互补后各时段的电能盈余和缺额均通过直接向电网购售电的方式来达到功率平衡，且［12:00，13:00］、［16:00，17:00］、［21:00，24:00］时段的212.769 kW总电能缺额（［12:00，13:00］、［16:00，17:00］、［21:00，24:00］时段分别为63.33、210.71、2 517.25 kW）被提前通过实体储能转移至电价峰时段（08:00，10:00］放出，CESO获得放电套利收益。同时，由于用户控制虚拟储能时存在充放电效率导致的名义上的电能损失，但CESO实则在（08:00，18:00］时段通过能量交换减少了部分电能损失，因此获得了用户“电能损耗”部分的套利收益。

用户层面虚拟储能的运行情况如附录A 图A4所示。由图可知：各用户在电价谷时段［00:00，08:00］对虚拟储能充电，以满足电价峰平时段的放电需求；（08:00，18:00］时段用户存在不同程度的需求互补现象，CESO 名义上满足了用户的充放电需求，但实际是将各用户的需求进行能量交换，并对电能缺额／盈余以购售电的方式实现配电网的功率平衡；18:00之后，各用户通过放电满足了电价峰平时段的用电需求，但CESO 仅在电价峰时段对实体储能放电来满足用户的放电需求，在电价平时段则以直接购电的方式满足各用户的需求，这对于用户而言，使用效果与其自配储能无异。

5.2.2 用户损耗成本贡献度分配及其改进结果

不同联盟下实体储能的损耗成本如附录A 表A5 所示。由表可知，用户联盟后实体储能的损耗成本低于单个用户参与CES服务时实体储能损耗成本的总和，这是因为联盟因需求互补减少了实体储能不必要的充放电损耗。采用Shapley 值法为用户分配其在大联盟｛1，2，3｝下的损耗成本贡献度，改进前、后的结果如表1所示。

表1 改进前、后各用户的损耗成本贡献度Table 1 Loss cost contribution degree of each user before and after improvement

由表1 可知，相较于联盟前各用户的损耗成本贡献度分配结果，若只考虑各用户参与其所在联盟的边际贡献（改进前），则用户1 — 3的损耗成本贡献度分别下降了284.158、48.440、188.906元，其中用户1 的损耗成本贡献度下降最大。观察图A4 可知，用户1 与用户2、3 在（08:00，18:00］时段的充放电互补性较强，而用户2、3 的充放电行为趋同，故分配结果合理。

分析改进后的影响效果如下：在能量互济率方面，K3，comp＜K1，comp＜K2，comp，用户1 — 3累计被消纳的新能源余量分别为1 035.29、618.89、1 668.68 kW，即用户3 的过剩新能源与其余用户匹配最多；在虚拟储能利用率方面，K3，use＞K2，use＞K1，use，用户3的租赁容量较大，却未能充分利用储能资源。观察图A4 可发现，用户3 整体的充放电程度较弱，虚拟储能利用率较 低。由 熵 权 法 得 到Ki，comp、Ki，use的 权 重 值 分 别 为0.32、0.68，设控制系数μ=0.5，以保证合作联盟内用户1 — 3的损耗成本贡献度491.61、144.99、442.61元分别小于非合作时用户1 — 3 的损耗成本贡献度835.05、227.82、537.85 元。由于虚拟储能利用率分摊系数的权重值较大，改进后的结果显示用户1、2的损耗成本贡献度减小，而用户3 的损耗成本贡献度增大。因此，相较于只考虑对损耗的边际贡献，在计及新能源余量能量互济率和虚拟储能利用率的影响后，再分配结果可促进用户将新能源余量充至虚拟储能中，以达成用户需求互补的目的，并可敦促用户按需租赁虚拟储能。

5.2.3 用户群体和CESO议价收益分配结果

改进损耗成本贡献度后CESO 和用户群体的议价迭代过程如图5 所示。由图可知，随着迭代次数的增加，双方期望的服务费系数逐渐逼近，最终在服务费系数为1.103时达成一致（小于误差限值），此时具有利益冲突的用户群体和CESO 达成彼此效益的帕累托最优，兼顾了双方的利益诉求。

图5 CESO和用户群体的议价迭代过程Fig.5 Bargaining iterative process between CESO and user community

进一步验证CES 服务的优势，设置如下2 种场景进行对比分析：①场景1，用户自配储能；②场景2，用户参与CES 服务。两场景中用户储能的规模及运行控制策略均相同。2 种场景的用户储能成本对比如表2所示，其中场景1的储能成本指充放电损耗成本，场景2 的储能成本指CES 服务费。由表可知：场景1 中各用户的储能成本均高于场景2 中各用户的CES 服务费，这是因为用户自配储能后充放电独立，因此其累计充放电功率较大（16 007.38 kW），产生了更多的充放电损耗；而场景2 中CESO 通过需求互补节省了充放电损耗（累计充放电功率为10 792.35 kW，节省了521.50 元储能成本）；当CESO的损耗成本越小时，其与用户议价时的定价权越低，所期望的服务费系数ηces越小，此时节省损耗所产生的效益也以服务费减小的形式反馈给各用户，相较于场景1，场景2 中改进后用户1 — 3 分别节省了292.80、67.89、49.64 元储能成本，且用户参与CES的另一优势在于无须自配储能，节省了储能投资成本。

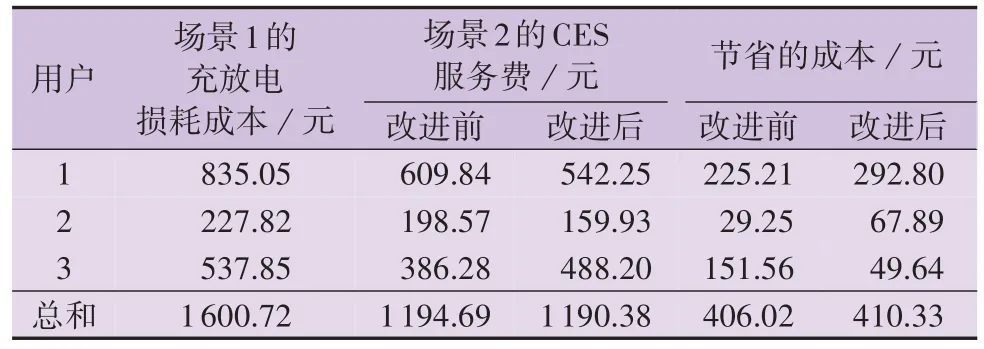
表2 2种场景的用户储能成本对比Table 2 Comparison of user energy storage cost between two scenarios

2 种场景中各主体的净收益结果对比如图6 所示，用户的净收益为节省的购电成本与储能成本之差。需要注意的是，此处CESO 的总体净收益除了其收取的服务费与实体储能损耗成本之差外，还包括其购售电收益Igridces。由图6 可知：场景2 中各用户参与CES 服务后的净收益均高于场景1 中各用户的净收益；且CESO 也因向用户收取服务费收回了储能损耗成本，获得了111.16 元利润及2 190.14 元套利收益。

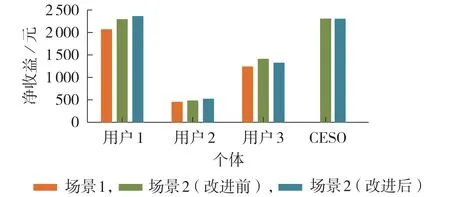
图6 2种场景中各主体的净收益结果对比Fig.6 Comparison of net income results of each entity between two scenarios

5.2.4 用户联盟对CES服务经济性的影响

由5.2.3 节的分析可知，CESO 的储能损耗成本是决定其服务费系数ηces的重要因素，而损耗成本的减小依赖于用户的充放电互补程度，其与联盟内部的充放电特性紧密相关。限于文章篇幅，本节仅探讨在包含用户1的3个联盟（｛1｝、｛1，2｝、｛1，2，3｝）下CES服务经济性的差异，结果见表3。

表3 不同联盟下用户1的CES服务费对比Table 3 Comparison of CES service fee of User 1 under different alliances

由表3 可知：联盟｛1｝中不存在充放电需求互补，用户1 需全额承担与其自配储能同等的储能损耗成本贡献度，且议价后CESO 需设定较高的服务费系数以保证自身有利可图，此时用户1 所缴纳的CES 服务费高于自配储能的损耗成本；联盟｛1，2｝中的充放电互补缓解了储能损耗成本的增大，但效益仍不显著，CESO仍需设定较高的服务费系数才能保证自身的利益；用户3 介入后，联盟｛1，2，3｝中的充放电互补性进一步增强，储能损耗成本的增大得到明显抑制，用户1 的CES 服务费甚至低于自配储能后的充放电损耗成本。可见，当CESO 聚拢大量具有较高程度充放电互补的用户时，其经济性才能得到显著提高。但无论是只存在少量用户的初期市场还是具有大量用户的成熟市场，各用户参与CES 服务后均无须自配储能，因此即使市场起步时用户的服务费较高，这也对用户有一定的吸引力。

5.2.5 考虑新能源出力不确定性的用能成本分析

本节对比2 种场景下的用能成本结果，用能成本由各主体的购售电成本和储能充放电损耗成本组成。本文中的虚拟储能运行模型未计及用户新能源出力波动性的影响，考虑一定的鲁棒性，建立用户鲁棒优化模型，具体见附录A 式（A14）—（A16）。设定预测误差θ=0.15，鲁棒系数τ的取值为0.7、0.8、0.9，不同τ值下2 种场景的用能成本对比如附录A 表A6所示。由表可知，随着鲁棒系数的增大，2 种场景的社会用能成本均增大，但在相同的条件下，场景2 的整体用能成本小于场景1 的整体用能成本，这表明当各用户参与CES 服务形成天然的联盟后，整体用能成本的减少不仅体现在CESO 通过充放电需求互补减少实体储能的多余损耗成本，还体现在CESO转移用户群体的总电能盈余和电能缺额所产生的购售电收益中，由此可见CES 服务在减小社会用能成本方面具有优势。

6 结论

本文基于所述CES 服务框架，提出了计及参与成本贡献的用户侧CES 服务及其纳什议价模型，实现了CESO 对用户提供的虚拟储能服务定价。经理论分析和算例仿真验证，得到如下结论。

1）用户参与CES 服务形成天然的联盟后，CESO通过对充放电需求互补的用户实现能量交换，有效减小了实体储能的充放电损耗成本，并提升了新能源的就地消纳率；对于用户群体各时段的用能盈余或缺额，CESO通过优化决策实体储能的充放电及购售电策略，减少了运行成本及总体用能成本。

2）采用Shapley 值法为各用户分配对实体储能损耗成本的贡献度，有效体现了用户在大联盟下因需求互补对损耗成本减少的影响；将各用户的损耗成本贡献度作为量化服务费差异性的依据，且结合各用户新能源余量能量互济率及虚拟储能利用率这2 个因素对其改进后，再分配结果可促进用户新能源余量的上网率及对虚拟储能的按需租赁。

3）在计及用户成本贡献的纳什议价模型中，通过求解统一的服务费系数，可在保证用户服务费差异性合理的前提下，兼顾用户群体和CESO 之间的利益诉求，促进双方的合作共赢。

本文对用户侧CES 定价进行了探究，为CES 业务的开展提供了一定的理论价值，后续将围绕CES容量规划、投资效益等方面进行进一步的研究。

附录见本刊网络版（http：//www.epae.cn）。