高压大容量储能功率转换系统的拓扑结构比较
吴传平,周天念,周特军,肖华根,谢 瑶,朱鸿章
(1.国网湖南省电力有限公司防灾减灾中心,湖南 长沙 410100;2.湖南科技大学 信息与电气工程学院,湖南 湘潭 411201;3.长沙理工大学 电气与信息工程学院,湖南 长沙 410114)
0 引言
随着新能源发电装机容量的比例不断提高,利用储能电池抑制新能源发电的随机波动性已成为国内外新能源发电领域的焦点。其中,功率转换系统(power conversion system,PCS)是储能系统的核心部件,其不仅决定了储能系统输出电能质量和动态特性,也影响着电池使用寿命[1]。在功率级数方面,PCS 可分为单级和双级;在拓扑方面,可用于10 kV及以上配电网的兆瓦级大容量储能PCS主要有变压器升压型变流器并联结构、H 桥链式多电平变流器、模块化多电平变流器(modular multilevel converter,MMC)等方案[2⁃3]。
变压器升压型变流器并联结构的优点是技术上容易实现,易扩容,储能直流电与电网交流电实现电气隔离,可防止电流直流分量进入交流电网;其缺点是体积较大,多个并联子系统之间易引发并联稳定性问题,系统总效率较低。早期储能PCS 由于开关器件的限制以及铅酸电池较低的充放电倍率和能量密度,多采用变压器移相多重化逆变技术实现[4]。H桥链式多电平变流器结构的优点是易于实现模块化,无隔离变压器,体积较小,重量较轻,效率较高,成本较低,将储能电池组并联接入H 桥链式多电平变流器的直流电容两端可以实现对巨量电池的“分割管控”,避免环流,安全性较高,电池管理系统的复杂性降低;其缺点是拓扑结构及控制系统较复杂,存在共模电流,相间桥臂需要电池荷电状态(state of charge,SOC)均衡控制[5]。文献[6⁃7]提出了H 桥链式多电平变流器拓扑结构在电池储能系统的应用研究,验证了功率控制和相内、相间的均衡控制。文献[8⁃9]对其主电路设计、功率控制、冗余控制和SOC均衡进行了研究,并指出不经过工频变压器而把储能系统直接接入中压电网,减小了损耗并降低了成本,该结构单机容量可达10 MW 以上,易于实现储能系统的大容量化。文献[10]针对H桥链式多电平变流器相间SOC 不均衡问题,提出了一种结合零序电压和负序电压注入的新型复合SOC 均衡控制策略,兼顾了储能装置的输出性能、相间SOC均衡能力和电能质量控制。MMC 的优点是易于实现模块化,无隔离变压器,体积较小,重量较轻,效率较高,成本较低,具有公共直流母线,适用于高压大容量储能系统;其缺点是拓扑结构及控制系统较H 桥链式多电平变流器拓扑结构更复杂,相间桥臂和上、下桥臂之间都需要SOC 均衡控制[11]。文献[12⁃13]对比分析了MMC 集中布置储能电池、分散布置储能电池以及级联H 桥电池储能系统(cascaded H bridge based battery energy storage system,CHB-BESS)的性能,指出MMC 分散布置储能电池效率最优,CHB-BESS效率次之,MMC 公共直流母线上集中布置储能电池效率最低。文献[14]对MMC 型电池储能系统(modular multilevel converter based battery energy storage system,MMC-BESS)的功率控制、模块均衡、桥臂均衡、相间均衡以及均衡增益的限制进行了分析和仿真。文献[15]对两级式MMC-BESS 的调制、功率控制、电池均衡和冗余控制进行了研究。文献[16]提出了一种基于MMC 的超导磁储能系统拓扑结构,该结构中的储能电池斩波器由多个子模块串联构成,可随MMC 扩展至多种电压等级和功率等级,且能均衡各子模块的电容电压。
综上所述,现有关于高压大容量储能PCS 的研究主要集中在控制策略方面,关于拓扑结构的研究很少,且仅进行了部分定性分析,未对3 种主要的高压大容量储能PCS 的拓扑结构进行全面的定量分析[17]。为了选择合理的高压大容量储能PCS拓扑结构,本文对变压器升压型变流器并联结构、H 桥链式多电平变流器、MMC 方案下的PCS 拓扑结构进行了理论与仿真比较研究。
1 变压器升压型高压直挂储能PCS
变压器升压型高压直挂储能PCS包括单级式变压器升压型PCS 和双级式变压器升压型PCS。其中,单级式变压器升压型PCS 通过预充电电路将储能电池接入三相脉宽调制(pulse width modulation,PWM)功率转换器直流侧,其结构见附录A 图A1;双级式变压器升压型PCS 通过双向DC/DC 变流器将储能电池接入三相PWM 功率转换器直流侧,其结构见附录A 图A2。相对单级式变压器升压型PCS,双级式变压器升压型PCS可以有效抑制电池侧二次脉动电流。
设绝缘栅双极型晶闸管(insulated gate bipolar transistor,IGBT)模块的单价为SIGBT,10 kV/380 V变压器的单价为ST,滤波电感的单价为SL,直流侧电解电容的单价为SC;储能系统的总容量为Pt,单台PCS的容量为Ps。单级式变压器升压型PCS包含NT1台变压器、NIGBT1台IGBT、NL1台滤波电感和NC1台直流侧电解电容,NT1、NIGBT1、NL1、NC1的表达式见附录A式(A1)。单级式变压器升压型PCS 的材料成本SSUM1为:
同理,双级式变压器升压型PCS 结构包含NT2台变压器、NIGBT2台IGBT、NL2台滤波电感和NC2台直流侧电解电容,NT2、NIGBT2、NL2、NC2的表达式见附录A 式(A2)。双级式变压器升压型PCS 的材料成本SSUM2为:
2 H桥链式高压直挂储能PCS
H 桥链式高压直挂储能PCS 中,每个功率转换模块包括单级式H 桥链式PCS 和双级式H 桥链式PCS。单级式H 桥链式PCS 拓扑结构如附录A 图A3所示。双级式H 桥链式PCS 通过附录A 图A2 虚线框所示双向DC/DC 变流器将储能电池接入单相PWM 功率转换器直流侧,其他部分的电路结构与附录A图A3相同。
H 桥链式高压直挂储能PCS 的功率转换模块还可由单相全桥变流器改为单相半桥变流器,使每个功率转换模块的IGBT 数量降低一半。但单相半桥变流器的直流侧电压利用率只有单相全桥变流器的一半。在此,只分析单相全桥功率转换模块结构的H桥链式高压直挂储能PCS。
令交流母线电压为UT_ac,单级式H 桥链式PCS的拓扑结构包含NIGBT3台IGBT、NL3台滤波电感以及NC3台直流侧电解电容,NIGBT3、NL3、NC3的表达式为:
单级式H桥链式PCS的材料成本SSUM3为:
式中:Udc为直流电压。同理,由双级式H桥链式PCS的拓扑结构包含NIGBT4台IGBT、NL4台滤波电感以及NC4台直流侧电解电容,NIGBT4、NL4、NC4的表达式分别为:
双级式H桥链式PCS的材料成本SSUM4为:
3 MMC型高压直挂储能PCS
在MMC 型高压直挂储能PCS 中,每个功率转换模块包括单级式MMC型PCS和双级式MMC型PCS。单级式MMC 型PCS 结构如附录A 图A4 所示。双级式MMC 型储能PCS 通过附录A 图A2 虚线框所示双向DC/DC 变流器将储能电池接入单相PWM 功率转换器直流侧。
单级式全桥MMC型PCS的材料成本SSUM5为:
同理,双级式全桥MMC 型PCS 中包含NIGBT6台IGBT、NL6台滤波电感和NC6台直流侧电解电容,NIGBT6、NL6、NC6的表达式为:
双级式全桥MMC型PCS的材料成本SSUM6为:
同理,单级式半桥MMC 型PCS 的材料成本SSUM7为:
双级式半桥MMC型PCS的材料成本SSUM8为:
4 不同拓扑结构的PCS比较分析
为了选择符合工程实际应用的最佳储能PCS拓扑结构,本文从系统可靠性、系统损耗、系统成本以及输出电流质量4 个角度,比较研究兆瓦级大容量储能系统拓扑结构。为了便于比较,所有拓扑结构中的功率开关器件均采用相同厂家和型号的IGBT,功率开关器件为常用的800 A 双管IGBT 模块,直流侧电压Udc为800 V,额定工作电流为300 A,开关频率均为f,交流滤波电感型号为300 A/0.7 mH,功率模块中直流电容型号为12 000 µF/450 V 的单位电容器,大容量储能PCS 的交流侧额定电压为10 kV,储能系统的总容量Pt为9 MW。
4.1 PCS的可靠性分析
影响系统可靠性的关键是主电路拓扑及所选器件的可靠性。对于双级式PCS,每个功率转换模块包括逆变侧的器件以及直流侧Buck-Boost 电路所含有的器件,其可靠性由所含有的IGBT、二极管以及电容器共同决定[17]。
定义逆变侧IGBT、二极管的可靠性分别为R1、R2,直流侧IGBT、二极管的可靠性分别为R3、R4,电解电容器的可靠性为R5;H 桥链式结构和MMC 结构的每个模块逆变侧有4 个IGBT 及反并联二极管,直流侧有2 个IGBT 及反并联二极管,同时还有1 个电容器。由此可以得到双级式H 桥链式PCS中功率模块j的可靠度RHj(t)为:
同理,得到双级式全桥MMC 型PCS 中功率模块j的可靠度RMj(t)为:
可靠性参数Ri(t)一般服从指数分布。Ri(t)表达式为:
式中:αi为第i种电力电子器件的失效率;时间t的单位为a。
因此,可以将双级式H 桥链式PCS 和双级式全桥MMC 型PCS 中单个H 桥功率模块的总可靠度RHU(t)统一表示为:
则基于k/m(G)评估模型的冗余度为k/m(m为PCS 中每链支路所含功率模块个数,k为PCS 中每链支路所含冗余功率模块个数)、每链支路含m个功率模块的双级式H 桥链式PCS 和双级式全桥MMC 型PCS的总可靠度Rsys( )
t可统一表示为:
式中:p为PCS 所含链式个数,双级式H 桥链式PCS中p=3,双级式全桥MMC型PCS中p=6。
系统平均无故障时间θsys( )t与可靠度间关系为:
故基于k/m(G)评估模型的冗余度为k/m、电平数为2(m-k)+1 的双级式H 桥链式PCS 的平均无故障时间θHsys(t)和双级式全桥MMC 型PCS 的平均无故障时间θMsys(t)分别为:
同理,由式(14)、(16)可得双级式半桥MMC 型PCS中单个半桥功率模块的总可靠度R0.5HU( )
t为:
则基于k/m(G)评估模型的冗余度为k/m、电平数为2(m-k)+1 的双级式半桥MMC 型PCS 的平均无故障时间θ0.5Msys(t)为:
为使分析结果具有可比性,假定变压器升压型PCS并联系统的容量、IGBT数量、功率模块冗余度与H 桥链式PCS 保持一致。则由H 桥链式PCS 和变压器升压型PCS的拓扑结构,可得变压器升压型PCS并联系统中功率模块数量m'与冗余模块数量k'分别为:
由于变压器的可靠性远高于IGBT、二极管、电容等器件,其失效率对PCS 总可靠性的影响可以忽略。变压器升压型PCS 的每个模块逆变侧有6 组IGBT及反并联二极管,直流侧有2组IGBT及反并联二极管,同时还有1 台电容器,则可得到变压器升压型PCS中单个功率模块的总可靠度RTU(t)为:
则基于k/m(G)评估模型的冗余度为k/m、总功率模块数为2(m-k)的变压器升压型PCS 并联系统的总可靠度RTsys(t)为:
变压器升压型PCS 并联系统中PCS 所含功率模块总个数、所含冗余功率模块个数、所含链式个数分别为2m、2k、1。则可得到变压器升压型PCS 并联系统的平均无故障时间θTsys(t)为:
由式(19)、(21)、(25)中θHsys(t)、θMsys(t)、θ0.5Msys(t)、θTsys(t)可知,当PCS 并联系统的容量及其功率模块冗余度一致时,无论αi如何变化,式(26)总成立。
由上述分析可知:当PCS 的系统容量及其功率模块冗余度一致时,变压器升压型PCS可靠性最高;当PCS 输出电压的电平数相同时,H 桥链式PCS 可靠性略高于双级式半桥MMC 型PCS,双级式半桥MMC型PCS可靠性高于双级式全桥MMC型PCS。
4.2 PCS的材料成本分析
上述8 种10 kV 高压大容量储能PCS 拓扑结构的材料成本函数及代入相关参数后的成本表达式可见附录A 式(A3)、(A4)。为便于比较成本,可根据各种器件的市场价格进行等价折算,将其他器件的单位成本统一折算为IGBT成本,成本折算关系式为:
式中:k1为PCS 中隔离变压器与IGBT 模块的成本之比;k2为PCS 中低压交流滤波电感与IGBT 模块的成本之比;k3为PCS 中高压交流电抗器与IGBT 模块的成本之比;k4为PCS 中子功率模块直流侧电容与IGBT模块的成本之比;SLL为PCS中低压交流滤波电感成本。当器件单位成本折算系数按市场价格确定后,则不同拓扑结构PCS 系统的总成本均为以IGBT单位成本为变量的函数,如式(28)所示。
根据式(28)可得表1 所示的器件单位成本折算系数与各种拓扑结构PCS的材料成本对应关系。表中:k5、k6分别为PCS 中隔离变压器与IGBT 模块的功率损耗之比、交流滤波电感与IGBT 模块的功率损耗之比;ΔPIGBT为IGBT的单位功率损耗;ΔPSUM1—ΔPSUM8为上述分析的8 种高压大容量储能PCS 拓扑结构的功率损耗。由表可知,对于单级式或双级式结构,H桥链式PCS 的材料成本最低,MMC 型PCS 的材料成本次之,变压器升压型PCS 并联系统的材料成本最高。
4.3 PCS的损耗分析
上述8 种10 kV 高压大容量储能PCS 拓扑结构的损耗计算函数见附录A 式(A5)。同理,为比较功率损耗大小,其他器件的单位功率损耗统一等价折算为IGBT 的单位功率损耗。各类器件的单位功率损耗折算关系式如式(29)所示,并将相关参数代入附录A 式(A5),则不同拓扑结构PCS 的功率总损耗均为以IGBT 单位功率损耗为变量的函数,功率损耗表达式如式(30)所示。
式中:ΔPT、ΔPL分别为变压器、滤波电感的单位功率损耗。根据产品手册确定各器件单位功率损耗折算系数后,由式(30)得到器件单位功率损耗折算系数与各拓扑结构PCS 的功率损耗对应关系如表1 所示。由表可知,H 桥链式PCS 的功率损耗最低,半桥MMC 型PCS 的功率损耗次之,变压器升压型PCS 并联系统的功率损耗最高。
4.4 PCS的输出电能质量分析
在电网电压一定的条件下,储能PCS 的输出电流谐波特性取决于交流滤波电感两侧的谐波电压差和滤波电感值的大小。而滤波电感值的选取属于参数设计范畴,因此当电感值一定时,选择储能PCS的输出电平数量直接决定其输出电流谐波特性。
无论哪种拓扑结构,当其电压等级和容量相同时,按各等效功率模块的输出电压相等进行等效,则等效功率模块的数量一致。因此,通过分析相同数量的单相电路等效功率模块所需器件及其产生的电平数量,可以比较分析不同拓扑结构在相同材料成本下的输出电流特性优劣。
根据上述比较分析,设单相PCS 中每链支路的等效功率模块数量为N时,变压器升压型PCS、H 桥链式PCS、全桥MMC 型PCS、半桥MMC 型PCS 的输出电平数量与功率开关器件数量的关系见附录A表A1。
在实际工程中,兆瓦级高压大容量储能系统中的PCS 所含H 型全桥功率模块总数在6 块以上。因此,由表A1可知:当总的等效功率模块数量相同,即储能PCS 容量相等,且交流侧滤波电感的滤波效果一致时,H 桥链式PCS 和半桥MMC 型PCS 拓扑结构的单位功率模块产生的输出电平数量最多,其输出电流特性最好,全桥MMC 型PCS 拓扑结构次之,变压器升压型PCS的输出电流特性最差。如果要求储能电池电流纹波可控,则选择双级式H 桥链式PCS和半桥MMC 型PCS 为最佳方案。附录A 表A1 中的2N、4N等表示等效功率模块数量为N时不同拓扑结构所含IGBT、直流电容等器件的数量,当应用于半桥型功率子模块时,上述与N的数量关系可由图A2 —A4 所示拓扑结构及半桥型功率子模块结构确定。
除此之外,当获得相同电平数时,半桥MMC 型PCS 的功率模块控制电路与交流侧滤波器数量比H桥链式PCS 多一倍;MMC 型PCS 的上、下桥臂电流存在以直流分量为主的环流,易引起电感饱和、降低可输出电流容量,而H 桥链式PCS 拓扑结构不存在该缺点。
根据上述工作可靠性、单位容量投资成本、系统损耗、输出电流质量等4 个方面的比较分析可知:H桥链式PCS和半桥MMC 型PCS是10 kV 大容量储能PCS的较优方案。
5 仿真建模与分析
5.1 仿真模型
变压器升压型PCS 拓扑结构、H 桥链式PCS、全桥MMC型PCS、半桥MMC型PCS的拓扑结构都具有单级式和双级式2种方案,且2种方案之间仅差一级双向DC/DC 变流器,用户可根据储能电池对电流纹波的要求及成本可接受度选择单级式或双级式;但逆变器部分为必要结构,故在此仅比较逆变器部分的性能指标。
10 kV 侧三相负载为:每相负载由2 Ω 串联8 mH 电感组成,通过补偿无功功率来检验PCS 输出电流质量。10 kV/6 MW 大容量储能PCS 的仿真方案及参数见附录A表A2。
5.2 仿真结果
5.2.1 方案Ⅰ:变压器升压型PCS并联方案
该仿真模型由24 台经变压器升压的储能PCS在升压变压器10 kV 侧并联而成。有功功率和无功功率给定值除以PCS 并联台数得到单台PCS 的有功功率和无功功率参考值,进而计算得到相应的有功电流和无功电流参考值;然后采用电流闭环控制策略控制每台变压器升压型储能PCS的输出电流。
方案Ⅰ的仿真结果如图1所示。图中:ia、ib、ic为储能PCS 的三相输出电流;ua为储能PCS 的单相输出电压。由图可知,每个子功率模块的直流侧电压即为PCS 的直流侧电压,PCS 的单相桥臂中点输出电压谐波分量较大,需要较大的滤波电感以控制输出电流的畸变率在合理范围内。
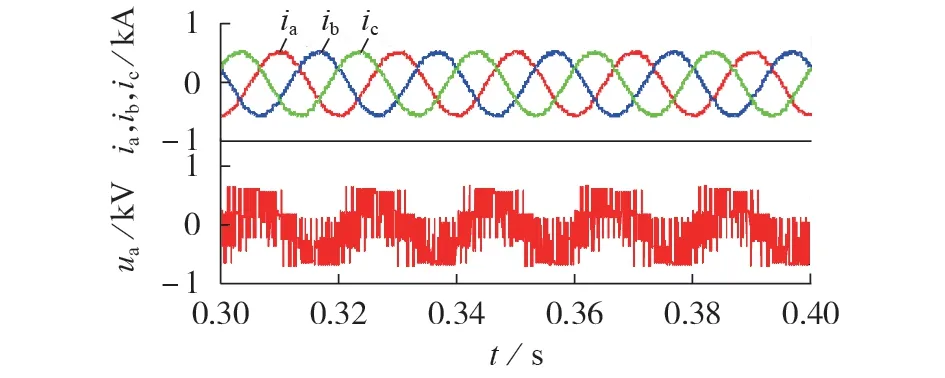
图1 变压器升压型PCS仿真波形Fig.1 Simulative waveforms of transformer step-up type PCS
5.2.2 方案Ⅱ:全桥MMC型PCS方案
该仿真模型中的每相全桥MMC 电路包括上、下2 个对称桥臂,上、下2 个桥臂各由8 个全桥H 型逆变模块级联而成,上、下2 个对称桥臂均通过0.7 mH滤波电感与第3个0.7 mH滤波电感连接,然后经第3个0.7 mH 滤波电感连接至10 kV 电网。该PCS 采用双闭环控制策略,外环为电压控制环,内环为电流控制环;调制策略采用载波移相控制。方案Ⅱ的仿真结果如图2 所示。由图可知,全桥MMC 型PCS 的单相桥臂中点输出电压的波形畸变率小,只需较小滤波电感就能保证输出电流的畸变率满足要求。
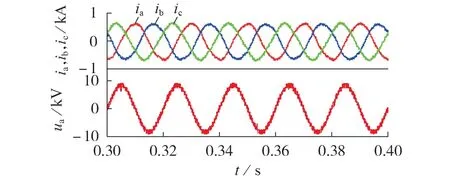
图2 全桥MMC型PCS方案仿真波形Fig.2 Simulative waveforms of full-bridge MMC-type PCS
5.2.3 方案Ⅲ:半桥MMC型PCS方案
该仿真模型中的每相半桥MMC 电路包括上、下2 个对称桥臂,上、下2 个桥臂各由8 个半桥逆变模块级联而成,上、下2个桥臂均通过0.7 mH 滤波电感与第3 个0.7 mH 滤波电感连接,第3 个0.7 mH 滤波电感连接至10 kV 电网。该PCS 采用双闭环控制策略,外环为电压控制环,内环为电流控制环;调制策略采用载波移相控制,同相电路上、下桥臂的相同序号子功率模块的载波信号相差22.5°。仿真结果如图3 所示。由图可知,半桥MMC 型PCS 的单相桥臂中点输出电压的波形畸变率小,只需较小滤波电感即可保证输出电流的畸变率满足要求。

图3 半桥MMC型PCS方案仿真波形Fig.3 Simulative waveforms of half-bridge MMC-type PCS
5.2.4 方案Ⅳ:H桥链式PCS方案
该仿真模型中的每相H 桥链式电路由16 个H全桥逆变模块级联而成,三相H 桥链式电路采用星形联结方式,交流侧经0.7 mH滤波电感连接至10 kV电网。该PCS 采用双闭环控制策略,外环为电压控制环,内环为电流控制环,且调制策略采用载波移相控制。仿真结果如图4 所示。由图可知,H 桥链式PCS 的单相桥臂中点输出电压的波形畸变率小,只需较小滤波电感即可保证输出电流的畸变率满足要求。
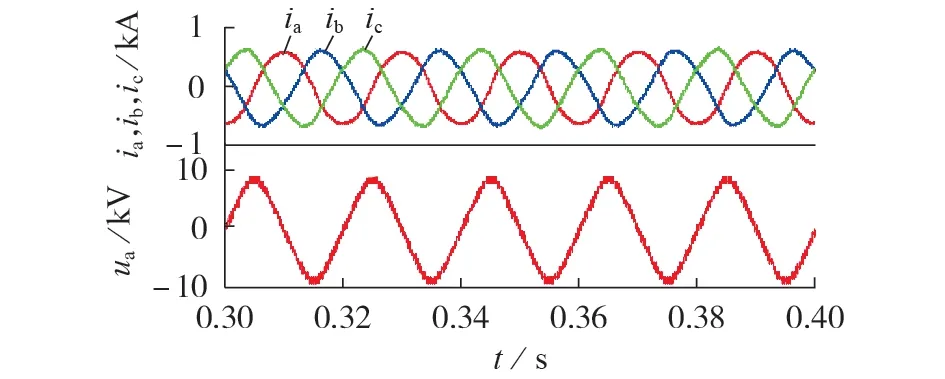
图4 H桥链式PCS方案仿真波形Fig.4 Simulative waveforms of H-bridge chain PCS
5.3 仿真结果分析
根据仿真结果数据及前面的材料总成本换算公式,得到4 种高压大容量储能PCS 方案的交流输出电流谐波含量及材料成本等参数如表2 所示。表中:S4500V-IGBT、S2500V-IGBT、S1700V-IGBT、S1400V-IGBT分别为额定电压为4 500、2 500、1 700、1 400 V 和额定电流为800 A的IGBT 价格;iaTHD、ibTHD、icTHD分别为储能PCS 的三相输出电流的总谐波含有率。
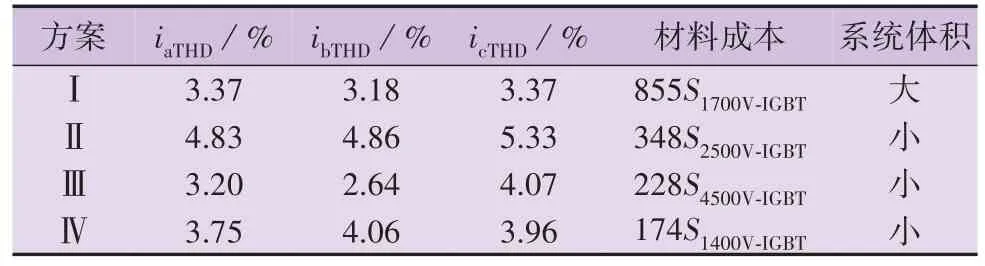
表2 10 kV/5 MW储能PCS输出电流谐波含量及材料成本Table 2 Harmonic content of output current of 10 kV/5 MW energy storage PCS and material cost
由于4 种典型高压大容量储能PCS 拓扑结构中的IGBT 电流大小相同,则额定电压等级越高的IGBT 越 贵,即S4500V-IGBT>S2500V-IGBT>S1700V-IGBT>S1400V-IGBT。由表2可知,当4种典型高压大容量储能电池PCS的输出电流质量基本相同时,综合考虑PCS 的交流输出电流质量、系统总成本和体积等方面,H 桥链式PCS 方案和半桥MMC 型PCS 方案较优,与理论分析结果基本一致。
6 结论
本文从工作可靠性、材料成本、功率损耗、输出电流质量等方面,对变压器升压型PCS、H 桥链式PCS、全桥MMC 型PCS、半桥MMC 型PCS 拓扑结构进行了理论比较分析和仿真验证,结果表明:上述4 种拓扑结构中,H 桥链式PCS 和半桥MMC 型PCS在构建10 kV 兆瓦级高压大容量储能PCS 时具有较优的综合性能指标。具体结论主要有:
1)当PCS并联系统的容量及其功率模块冗余度一致时,变压器升压型PCS 的可靠性最高,H 桥链式PCS次之,全桥MMC型PCS最低;
2)H 桥链式PCS 的总成本最低,半桥MMC 型PCS 的总成本次之,变压器升压型PCS 的总成本最高;
3)H 桥链式PCS 与半桥MMC 型PCS 的总损耗最低,全桥MMC 型PCS 的总损耗次之,变压器升压型PCS的总损耗最高;
4)当等效功率模块总数相同,即储能PCS 容量相等,且交流滤波电感的电感值一致时,H 桥链式PCS 与半桥MMC 型PCS 的输出电压电平数量最多,输出电流特性最好,全桥MMC 型PCS 结构次之,变压器升压型PCS 的变流器输出电流特性最差,但是由于升压变压器的绕组相当于电感,特别是低压侧采用三角形接法时,升压变压器对谐波电流也具有较好抑制效果。
附录见本刊网络版(http://www.epae.cn)。

