基于简化HMM和时间分段的非侵入式负荷分解算法

刘 凯，符 玲，杨金刚，熊思宇，蒿保龙，刘丽娜

（1.西南交通大学 唐山研究院，河北 唐山 063000；2.西南交通大学 电气工程学院，四川 成都 611756；3.国网四川省电力公司计量中心，四川 成都 610045）

0 引言

以高级量测体系（advanced metering infrastruc⁃ture，AMI）等技术作为支撑，家庭用户与供电公司之间的关系由原来的家庭用户单方向用电发展为家庭用户与供电公司双向灵活互动。负荷监测是AMI的一种重要功能，可为供电公司提供详细的用户用电数据信息，同时也可使用户更清晰地了解自己的用电行为，从而帮助用户／供电公司选择更节能高效的用电／供电策略。

负荷监测按照各种设备级负荷数据的获取方式分为侵入式负荷监测（intrusive load monitoring，ILM）和非侵入式负荷监测（non-intrusive load monitoring，NILM）。相比于直接获取负荷数据的ILM，NILM 更依赖于算法，通过分解在用户电力入口端测量的集总数据得到用户家庭内部各种设备的用电详情［1］。NILM 由于具有更好的经济性和隐私保护性，受到了大量学者的关注［2］。NILM 的求解需要以负荷特征作为支撑，根据数据的不同采样频率，可以将负荷特征分为高频（频率大于1 Hz）特征和低频（频率不大于1 Hz）特征［3］。高频特征主要包括负荷的电流谐波、电压-电流轨迹、高频暂态波型等，低频特征包括负荷的有功功率、无功功率、电流有效值等。虽然高频特征包含更多的负荷信息，但是现有AMI 中的智能电表一般仅提供低频数据的采集支持［4］，要获得高频特征就需要额外添加采集设备，这会增加经济和人工成本，因此，利用智能电表提供的低频特征数据来实现居民家庭的负荷分解，是一种具有实际应用价值的方案［5］。

负荷分解算法可以分为2 类。一类是组合优化，如：文献［6］提出利用时间概率因子来改进目标函数，再利用遗传优化算法进行负荷分解，该算法的准确率高但求解时间长；文献［7］结合改进的交叉熵算法和惩罚函数，通过迭代更新概率求取最优解并将其作为分解结果。另一类是模式识别，如：文献［8］利用各种电器间的关联规则，基于信息熵和k近邻算法实现状态辨识，但仅考虑两两负荷之间的关联；文献［9］提出利用模体挖掘的方式，结合事件检测与调和函数进行事件匹配和设备识别，但算法依赖于运行窗的选取。近年来，随着神经网络的发展，利用神经网络来实现负荷分解也受到了研究人员的关注，如：文献［10］提出利用深度神经网络，综合电器的时间和功率信息进行负荷分解，但是模型参数的训练需要大量的历史数据和时间。在负荷分解的求解算法中经常采用隐马尔可夫模型（hidden Markov model，HMM），如：文献［11］为每种负荷均建立一条HMM 链，再结合二次整数规划进行求解，通过假设初始分布概率相等简化了部分运算，但是算法的计算复杂度较高；文献［12］为一天中的每个小时单独建立HMM，再结合行为影响因子来实现负荷辨识。总体而言，现有的低频负荷分解算法模型复杂，求解时间长，在部署监测设备方面压力较大。此外，大部分算法需要将前一个或多个时刻的分解结果作为当前时刻分解的依据，若前面的分解结果出错，则会造成误差累积。

基于以上分析，本文提出一种利用有功功率，并在每个时刻独立求解的负荷分解算法。首先，在训练阶段，利用改进的亲和力传播聚类算法自适应地获取负荷功率模板，并将数据按照时间分段；然后，对HMM 进行简化，构建负荷分解算法，并在不同的时间段内分别训练模型参数，在负荷分解阶段，结合时间信息实时求取用户负荷功率组合；最后，基于2 个国外的低频公开数据集的测试结果表明，本文算法准确率高且所需的求解时间短。

1 负荷的超状态编码

1.1 负荷分解

假设居民家庭内部共包含M个负荷，任意负荷i的有功功率Pi≥0，则在t时刻用户总的有功功率可以表示为：

式中：s为t时刻负荷i是否运行在状态n的标志，若运行在状态n，则其值为1，否则为0；pi，n为负荷i在状态n下的功率模板。通常，在正常工作情况下，负荷功率模板不会发生变化，因此，在确定负荷功率模板后，负荷功率分解问题就可以表示为t时刻所有负荷状态的求解问题。

1.2 负荷状态编码

可以将居民家庭中的负荷按照运行时可能出现的状态分为只存在开关状态的Ⅰ型负荷、具有有限运行状态数的Ⅱ型负荷、状态可以连续变化的Ⅲ型负荷以及一直处于某一功率运行的Ⅳ型负荷［13］。当负荷为Ⅰ型负荷时，以“0”表示关闭状态，以“1”表示开启状态；当负荷为Ⅱ型负荷时，以有限位数的“0”“1”组成的向量表示负荷状态；当负荷为Ⅲ型负荷时，负荷功率特征在有限的范围内连续变化，一般通过聚类的方式对负荷状态进行离散化，从而将其转化为有限种状态［8］；当负荷为Ⅳ型负荷时，可以将其等效为缺少“0”状态的前3 种负荷。由于通过聚类可将所有负荷均等效为有限状态机，因此，采用独热码来表示各种负荷状态［14］。对于拥有Ni种状态的负荷，其独热码位数为Ni，且对于任意给定的状态，独热码向量的各元素中仅有1 个元素置1。若将整个家庭所有负荷的独热码按顺序拼接，则可以将家庭中所有的负荷状态表示为1个超状态向量S［15］，如式（3）所示。

式中：sk(k=1，2，…，K)的取值为0 或1，K为所有负荷的运行状态总数。例如，假设用户家庭中只有电灯和洗衣机，其中电灯为Ⅰ型负荷，只有开关状态，洗衣机为Ⅱ型负荷，有浸泡、洗涤、脱水3 种开启状态，则可以在超状态向量中用第1 个元素表示电灯的状态，第2 个元素表示洗衣机的浸泡状态，第3 个元素表示洗衣机的洗涤状态，第4 个元素表示洗衣机的脱水状态，若S=[0，1，0，0]，则表示电灯处于关闭状态，洗衣机处于浸泡状态。

2 负荷功率模板的获取

获取负荷功率模板是进行负荷分解的重要前提，考虑到每种负荷的运行状态数未知，K-means 和模糊C均值聚类算法需提前确定聚类中心数［16］，而亲和力传播（affinity propagation，AP）算法不需要提前确定最终的聚类中心数，因此，本文利用AP 算法来获取负荷功率模板。

2.1 聚类数据的预处理

AP 算法需要人为调整的参数少，降低了人为因素对结果的干扰［17］。AP 算法的具体计算流程参考文献［17］，该算法主要包括相似度矩阵E、归属度矩阵A和吸引度矩阵R这3 个参数矩阵。算法所需时间和计算结果受到样本点数的影响：当聚类的样本点过少时，聚类结果会不准确；当聚类的样本点过多时，算法的计算时间会增加。因此，本文提出对大量的样本进行分层抽样，在满足较长时间跨度的同时，减少样本点。

本文采用的分层抽样规则如下：

1）由于实际运行时负荷处于关闭状态的时间远长于处于开启状态的时间，同时考虑到噪声干扰，先剔除负荷功率小于10 W的部分；

2）将10 W 与最大功率之间的部分等分为5 层，在每层随机抽取α个样本点，对于样本点数不足的层，保留该层的全部样本点；

3）将样本点数小于5 的层中所有数据剔除，消去异常样本点的干扰；

4）对剩余的样本点进行聚类。

通过分层抽样可将尽可能多地反映负荷运行状态的数据作为聚类依据，同时剔除了异常点，减少了用于聚类算法的样本点。

2.2 AP算法的改进

在传统AP 算法中，当归属度矩阵A和吸引度矩阵R的计算结果在一定的迭代次数内保持不变或者迭代达到设定次数时，停止迭代，并且聚类中心c由式（4）确定。

在确定各点所属的簇中心时，会出现由式（4）得到节点ci和节点cj均为聚类中心，但节点cj所属簇中心的计算结果却为节点ci的情况。传统AP 算法直接将节点cj所属簇中心强制确定为节点cj，这会造成2 个相近的点被划分至2 个簇的情况。为了避免产生相近的簇中心，本文将节点cj和归属于节点cj的所有点都重新划归为属于节点ci。

此外，最终的聚类中心数受到参考度取值的影响。在得到聚类中心后，可以计算各点到其聚类中心的距离之和D，D的大小能够反映聚类中心数的合理性。聚类中心过多的极限情况是每个点均为聚类中心，此时D为0；聚类中心过少的极限情况是聚类中心只有1 个，此时D的最大值为样本点到其余样本点距离之和的最大值，即相似度矩阵中绝对值最大的列元素之和。为了使不同分布状况的负荷均能获得适宜的簇中心，求取D与相似度矩阵中列元素之和最小值的比值γ，再限定该比值的范围，并以该范围为依据，采用迭代更新的方式自适应选择每种负荷的参考度，具体方法如下。

1）由于参考度绝对值越接近0，最终的聚类中心数越多，因此，初始参考度选取为所有样本点两两之间距离中值的1/4，通过聚类得到各点所属的簇，并计算D。

2）将γ与阈值进行比较。通过实验，本文选取阈值为0.01 和0.1，即当γ小于0.01 时，减小参考度，当γ大于0.1 时，增大参考度，并重新聚类获取聚类结果，直到满足范围要求。

最终，负荷功率模板的获取过程包括聚类前的样本点分层抽样、聚类时相近簇中心的剔除以及参考度的自适应迭代更新，具体如附录A 图A1 所示。在通过聚类得到各负荷功率模板后，可以计算超状态向量S的元素数，再将S与负荷功率模板Ptem位置一一对应。式（2）可以表示为：

式中：St为t时刻的超状态向量。

3 HMM的简化与分时段负荷的分解

3.1 HMM的简化

HMM 主要包括负荷的初始概率分布矩阵π、负荷的状态转移概率矩阵Z以及表示负荷状态与功率关系的发射矩阵B这3 个参数矩阵。基于HMM 的负荷分解算法满足马尔可夫链的齐次假设，即马尔可夫链的一步转移概率与马尔可夫链所处时间无关。但是，考虑到用户的用电习惯，各种负荷在不同时间段内运行的概率不同，这导致π、Z、B也不同。此外，HMM 需要根据前一时刻的负荷状态分解结果，结合状态转移概率矩阵Z来求解当前时刻的状态，若前一时刻负荷的状态识别结果与真实情况不符，则会影响后续的负荷分解结果。

本文将HMM进行简化：①不考虑状态转移概率矩阵，只保留π和B，从而在算法求解时减少运算量，缩减计算时间；②在参数学习阶段，通过用户家庭的历史用电数据减少超状态种类数，并通过时间分段进一步限制在不同时间段内可能出现的超状态种类数，同时，分别在不同时间段通过训练获取π和B，从而在这2个矩阵中保留各负荷在不同时间段的运行差异信息。

3.2 时间段的划分

按照一般用户家庭生活习惯，可以将一天划分为睡觉时间段、与饮食相关的时间段、晚饭后的休闲娱乐时间段以及上述各时间段之间的过渡时间段。本文将一天划分为11 个时间段，其中01:00 — 05:00为第1 个时间段，将其余时间段按照2 h 为1 个时间段进行划分，如附录A图A2所示。

3.3 超状态参数的获取

根据负荷功率模板，将训练集中各负荷功率序列标记为负荷状态，将训练集数据按照时间段划分为各子数据集，在每个时间段，统计超状态的种类数，计为Jλ。初始概率分布矩阵πλ可以表示为：

式中：V（λλ=1，2，…，11）为第λ个时间段内的样本总数；VSj(j=1，2，…，Jλ)为超 状态向 量Sj下的样本点数。

在每个时间段计算超状态的发射矩阵Bλ∈RJλ×Oλ，Oλ=P-P+1 为在第λ个时间段总功率的取值区间，P、P分别为第λ个时间段总功率的最大值和最小值。为了减小发射矩阵的维数，将功率值取整。发射矩阵的元素bjo表示当用户家庭整体状态构成超状态向量Sj时功率观测值为o的概率，计算公式为：

式中：Hjo为超状态向量Sj下功率观测值为o的频数；Hj为超状态向量Sj下的总频数。

3.4 负荷功率分解

算法的输入为总功率的观测值ot及其对应的时间信息。基于分时段初始概率分布矩阵和发射矩阵的功率求解步骤如下。

1）利用输入的时间信息选择不同时间段的初始概率分布矩阵πλ和发射矩阵Bλ。

2）由ot确定发射矩阵中的列，t时刻估计的超状态矩阵为：

式中：argmax 为求参函数。由于Bλ中每行对应一种超状态，因此，式（8）实际是求取使得概率值最大的行数，从而确定对应的超状态。

3）由超状态和负荷功率模板矩阵解码求得各负荷在t时刻的功率值。

4 算例分析

4.1 算法评估指标

负荷识别结果准确率指标主要包括负荷状态识别准确率指标和负荷功率分解准确率指标。

为了便于与现有方法进行对比，本文选择文献［18］定义的有限状态识别准确率指标F1，计算公式为：

式中：p为识别为开启状态样本的分解结果中正确结果的比例；r为真实开启状态样本的分解结果中正确结果的比例；Tp为正确识别负荷处于开启状态的次数；Fp为负荷实际处于关闭状态但识别结果为开启状态的次数；Fn为负荷实际处于开启状态但识别结果为关闭状态的次数；Tinacc为附加惩罚项，引入该变量是由于对于有多种开启状态的负荷，存在虽然识别结果和实际都是开启状态但识别的具体开启状态与实际不符的情况，其计算公式如式（12）所示。

式中：T为测试集的总时长包含的时刻数；、st，i分别为t时刻负荷i的估计状态和真实状态，当估计状态和真实状态不同时，两者差值为1。

负荷功率分解准确率apower也常用于评估负荷识别的效果［19］，计算公式为：

4.2 分解结果

为了测试算法效果，本文选取2 个由真实家庭采集的低频数据集REDD（reference energy disag⁃gregation dataset）［20］和AMPds（almanac of minutely power dataset）［21］，其中REDD 来自美国波士顿地区的多个家庭，约每3 s 进行1 次负荷功率数据的采集和储存。AMPds 记录了温哥华地区1 户居民2 a 的功率数据，每1 min进行1次数据记录。同时，这2个数据集均以时间戳为时标对每个数据进行标注，结合地理时区划分能够得到每个数据在当地的具体时间，方便进行时间段的划分。

1）在REDD上的测试。

将文献［11］基于二次规划的因子HMM 算法和文献［12］利用行为影响因子的HMM 算法与本文算法进行对比，选取相同的家庭1、2、3、6 进行测试。为了获取负荷在各时间段内的参数以及功率模板，将前2 周的数据作为训练集，将其余数据作为测试集，负荷功率分解准确率对比如表1所示。

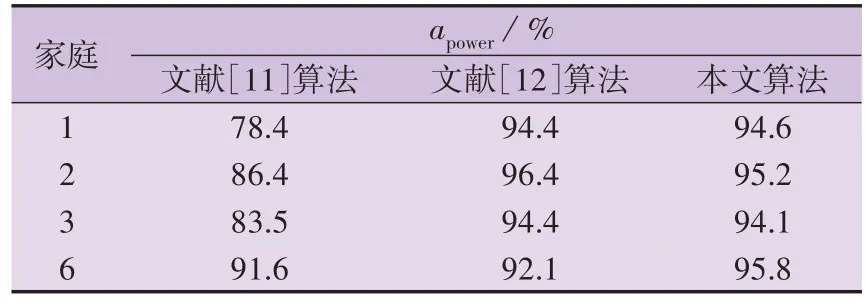
表1 负荷功率分解准确率对比Table 1 Comparison of load power decomposition accuracy rate

由表1 可知，本文算法的负荷功率分解准确率均高于文献［11］算法，本文算法对家庭1和家庭6的负荷功率分解准确率高于文献［12］算法，对家庭2和家庭3 的负荷功率分解准确率与文献［12］算法相当。

为了便于验证本文算法对单个负荷的识别准确率，选择与文献［7］中场景5 相同的实验设置，并与该文献中的改进交叉熵（modified cross-entropy，MCE）算法和分段整数约束规划（segmented integer quadratic constraint programming，SIQCP）算法进行对比，分解结果如附录A 表A1 所示。由表可知：本文算法对大多负荷的识别效果均更具优势，且整体识别效果优于文献［7］算法；虽然本文算法对个别负荷（如烤箱）的识别效果与文献［7］算法差距很大，但是整体识别效果和F1是将整个测试阶段的所有负荷分解结果作为整体进行计算的，烤箱等负荷使用较少，对整体结果的影响很小。

2）在AMPds上的测试。

相较于REDD，AMPds 的时间跨度更大，采样频率更低，与实际的智能电表数据更接近。选择文献［7］中的场景3对MCE算法和本文算法进行对比，同样选择600 h 的测试数据，选择相同的7 种运行频次较高的负荷，即地下室、干衣机、洗碗机、暖通空调、冰箱、热泵、壁炉。用于训练的数据时长为40 d，识别结果准确率如表2所示。

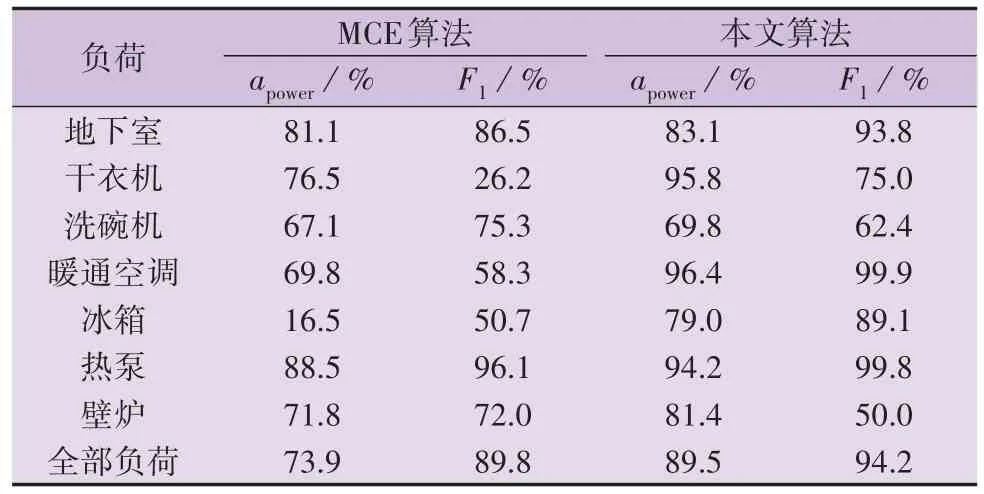
表2 各负荷识别结果准确率Table 2 Accuracy rate of identification results for each load

由表2 可知，本文算法总的负荷功率分解准确率达到了89.5 %，且有限状态识别准确率达到了94.2 %，比MCE 算法的计算结果有了较大幅度的提高，这表明本文算法可得到较好的负荷分解结果，其中，暖通空调主要是在夜晚使用，以保持室内温度舒适，具有较强的时间段分布特性，因此本文算法对暖通空调的识别准确率提升幅度较大。

为了验证本文算法在较长时间下的分解准确率以及算法训练集时长对准确率的影响，设计包含8 种负荷（在前文7 种负荷的基础上增加电视机）的4 种情景：场景1 — 4 分别利用20、40、60、80 d 的历史数据训练参数，再对360 d 的数据进行分解，负荷识别结果准确率如表3所示。

表3 不同时长的负荷识别结果准确率Table 3 Accuracy rate of load identification results for different time lengths

由表3 可知，当用于训练的数据时长达到40 d后，识别结果准确率趋于稳定，延长训练时长不会显著提高识别结果准确率，且当用于训练的数据时长为40 d时，负荷功率分解准确率能够达到90.0 %，有限状态识别准确率能够达到90.7 %。

将场景2 下本文算法对各负荷的分解结果与真实值进行比较，结果如表4 所示。由表可知：本文算法对电视机功率的分解值与真实值间有较大差别，达到3 %，这主要是由于在AMPds 中电视机的子数据集并非仅记录了电视机的功率数据，还包括个人录像机顶盒、音箱等设备的数据，这些数据构成一个合成的待机状态功率，在整个数据集中的第132 天，待机状态功率由39 W 降到19 W，并在之后保持不变，而场景2 的负荷功率模板是通过对数据集前40 d的数据进行聚类而获取的，因此，无法描述该差别，从而给分解带来了误差；本文算法对其他负荷功率的分解值与真实值均较接近。

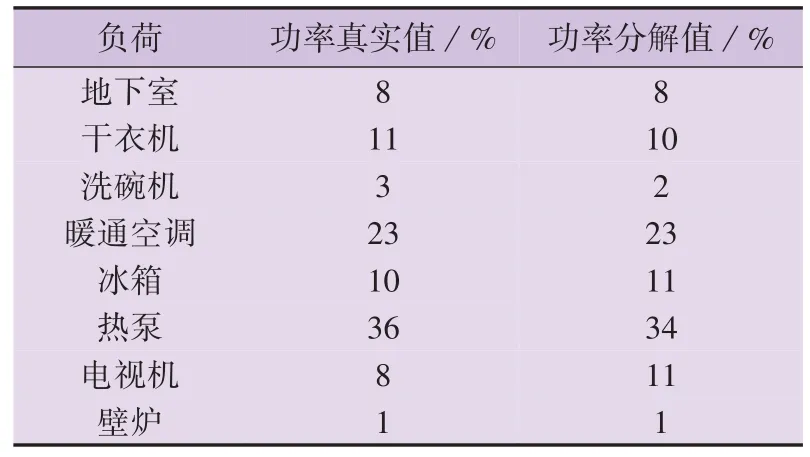
表4 场景2下各负荷消耗的功率Table 4 Power consumption of each load under Scenario 2

4.3 算法复杂度分析

本文算法不考虑HMM中的转移概率矩阵，且利用独热码对负荷状态进行编码缩短了算法所需时间。由于训练阶段可离线进行，且参数训练完成后可以离线调用，因此，不考虑训练阶段的计算时间。假设在负荷分解时各时间段内最大的超状态数为G，在求解时输入观测值ot后，得到对应的发射矩阵中的列索引，再将发射矩阵的该列向量与初始概率矩阵进行按位乘法运算，即最多进行G次乘法运算，因此，算法的最大复杂度为O（G）。实际上，由于发射矩阵具有稀疏性，某一确定的观测值对应的超状态数远小于G，因此，复杂度也小于O（G）。本文的测试软件为MATLAB R2021b，硬件为搭载了Intel（R） Core（TM） i5-7300HQ、内存为8 GB 的笔记本电脑。

在长时间数据集AMPds 上进行测试，分别选取2、4、6、8种负荷，待分解的时长为1～12个月，每天的数据点数为1 440。本文算法分解所需时间如附录A图A3所示。由图可知，本文算法可以在短时间内完成负荷分解。为了分析本文算法在每个测试数据点的平均分解时间，将其与文献［12］添加行为影响因子的HMM算法和文献［15］的扩展稀疏HMM算法进行对比，结果如表5所示。

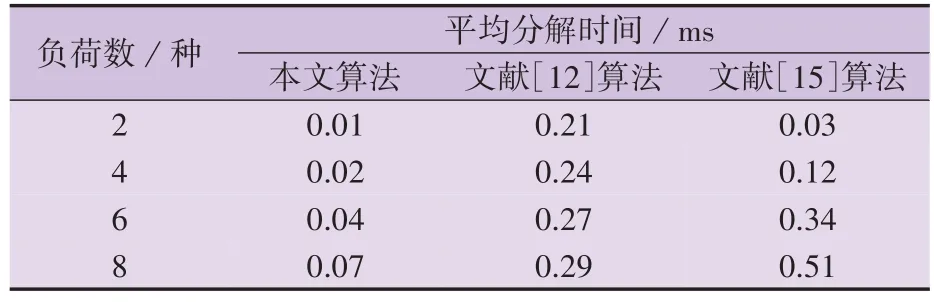
表5 平均分解时间Table 5 Average decomposition time

由表5可知，本文算法相比文献［12］和文献［15］算法在平均分解时间上均具有明显优势。此外，为了分析本文所提简化HMM 与传统HMM 在准确率和求解时间上的差异，选择与表3中场景2相同的负荷种类及训练时长，并采用相同的负荷功率模板，采用MATLAB 2021b 中集成的hmmestimate 函数和hmmviterbi 函数对模型进行训练和求解，测试结果如附录A 图A4 所示。由图可知，相较于传统HMM，简化HMM在长时间下的分解准确率更高，且在计算时间上具有显著优势。

5 结论

由于现有AMI 的低频采集条件，利用低频有功功率进行居民家庭NILM 更具可实施性。针对传统算法对于分解结果的依赖性，本文提出一种在各时刻独立求解的实时非侵入式负荷分解算法。本文算法在2 种公开数据集上的负荷功率分解准确率和有限状态识别准确率均不低于90 %，并且算法的计算时间短，对含有8 种负荷场景的平均分解时间仅为0.07 ms。

笔者后续将进一步考虑不同用户负荷类型以及用电行为的相似性，并进一步简化模型参数的获取过程，从而使得算法更具泛化性。

附录见本刊网络版（http：//www.epae.cn）。