计及不确定性的风储联合系统多时间尺度市场参与策略

孙 鑫，魏文荣，李琼林，姚福星，刘 阳，张亚飞，苗世洪

（1.国网河南省电力公司电力科学研究院，河南 郑州 450052；2.华中科技大学 电气与电子工程学院 强电磁工程与新技术国家重点实验室电力安全与高效湖北省重点实验室，湖北 武汉 430074）

0 引言

随着“双碳”发展目标的提出，深入推进能源结构调整、加快构建以新能源为主体的新型电力系统已势在必行。虽然新能源出力具有明显的反调峰特性，但储能优秀的能量时移特性为高比例新能源接入提供了条件。2021年7月，国家发展改革委、国家能源局印发了《关于加快推动新型储能发展的指导意见》，正式提出“新能源+储能”电站的运营模式［1］。同年12 月，广东省能源局发布《南方（以广东起步）电力现货市场实施方案（征求意见稿）》，提出建立健全适应新能源为主体的新型电力系统市场交易机制［2］，这意味着“新能源+储能”电站将有机会作为独立主体参与电力市场［3］。在此背景下，以风储联合系统（wind-energy storage combined system，WCS）为例，研究“新能源+储能”作为独立主体的电力市场参与策略，具有重要的理论和现实意义。

依据交易商品类别的差异，现行电力现货市场主要分为能量市场、辅助服务市场［4］。但目前由于储能造价高昂，若仅考虑WCS 参与能量市场，则投资成本回收周期较长。然而，若WCS 同时参与能量市场、辅助服务市场，则既可发挥储能的快速功率响应能力［5］，提高资源的利用率，又可获得额外的收益，加速投资成本回收。因此，国内外学者对WCS参与多类型市场的投标策略进行了大量的研究。文献［6］在计及荷电状态对调频表现影响的基础上，建立了WCS 参与能量市场、调频辅助服务市场的投标模型。文献［7］结合我国某WCS 示范项目，建立了虚拟电厂参与能量市场、调频辅助服务市场、调峰辅助服务市场的优化模型，并基于模拟退火算法计算风电、储能出力。然而，上述研究均未考虑风电出力波动带来的偏差功率影响，研究成果具有局限性。

风电出力具有强不确定性，因此风电预测功率与实际发电功率之间总存在无法忽略的偏差功率，偏差功率的存在阻碍了投标计划的精准执行。当WCS 的实际发电功率未达到计划要求时，市场决策机构将根据功率缺额对其进行偏差惩罚；当WCS 的实际发电功率超出计划要求时，将导致弃风现象，这会浪费电站的投资建设和维护成本，给电站造成经济损失。可见，高额的偏差惩罚和弃风损失（devia⁃tion penalty and wind curtailment loss，DPWCL）会大幅削减WCS 的净收益。为此，对风电出力不确定性进行量化建模，力求降低偏差功率对WCS 经济收益负面影响的意义重大。文献［8］基于场景分析法模拟了风电出力不确定性，并引入风险规避因子，建立了含偏差风险规避的风储协同参与市场策略。文献［9］假设风速服从韦伯分布，利用场景生成和削减方法处理风电出力不确定性，建立了考虑风电投标偏差惩罚的电力市场随机均衡模型。文献［10］考虑风电出力不确定性、储能寿命损耗，建立了风储联合参与能量市场、快速调频辅助服务市场的优化投标模型，并基于近似动态规划进行求解。然而，上述研究在概率建模、场景生成过程中未考虑风电预测出力与实际出力的非线性相关性，而是人为假设预测误差统一服从某概率分布，分析结果的可信度有待提高。同时，上述研究仅依据日前尺度的风电预测出力进行投标决策，未考虑日内功率预测精度提升对投标决策的影响，投标决策的有效性存在不足。

为了提高WCS投标决策的准确性，增加WCS在电力市场的净收益，本文首先基于Copula 函数对风电出力的强不确定性进行精确建模，并以此为基础预留部分储能出力能力，从而减小偏差功率的影响；然后，以WCS 预期净收益最大为目标，制定能量市场、调频辅助服务市场的日前投标模型，并在日内阶段根据超短期风电预测数据修正日前上报计划，提出考虑风电出力不确定性的WCS 多时间尺度市场参与策略；最后，结合我国某实际WCS 的实测数据进行仿真，结果验证了所提策略的有效性，并对其在我国电力市场背景下的应用进行了分析和展望。

1 WCS 参与能量市场和调频辅助服务市场的机制框架

目前，储能成本昂贵，采用风储联合方式进行能量交易的单一模式难以快速回收其投资成本，而兼顾提供辅助服务的运营模式已成为WCS 的主要盈利手段之一［11］。为了实现收益最大化，WCS 在日前制定上报计划时，通常将可调用储能完全投入能量市场和辅助服务市场［6］，但受新能源出力不确定性强、储能预留出力能力不足等因素的影响，在次日实际运行时，WCS又会因功率偏差而遭受市场惩罚。

本文借鉴美国宾夕法尼亚—新泽西—马里兰州（Pennsylvania-New Jersey-Maryland，PJM）联合电力市场机制，设定WCS 通过参与能量市场和辅助服务市场获利，提供的辅助服务为调频服务。显然，能量市场和调频辅助服务市场均为竞争性市场，但WCS作为新能源发电商，其并网容量远小于发电集团，其竞价行为对市场出清价格的影响很小，因此可将WCS作为电力现货市场的价格接受者［12⁃13］。

1.1 能量市场和调频辅助服务市场的收益模型

依据时间尺度的差异，能量市场被分为日前能量市场和实时能量市场。在PJM 市场机制下［14］：参与日前能量市场的发电商须在12:00前完成投标，市场于16:00前完成出清计算并公布交易结果；参与实时能量市场的发电商须在16:00 — 18:00时段内完成投标，市场于次日实际运行前滚动出清［15⁃16］。由于实时能量市场在18:00 关闭，WCS 无法随次日更新的超短期风电预测数据修改上报计划，且无法在日前得知市场交易结果，因此本文不考虑WCS 参与实时能量市场。日前能量市场的时间框架见附录A图A1。

WCS在能量市场的收益模型为：

式中：We，t为t时段WCS 在能量市场的收益；ce为能量交易电价；Pt为t时段能量市场的上报功率；Pw，t和Pch，t、Pdis，t分别为t时段的风电计划调度功率和储能充、放电功率；Δt为投标时段间隔。

在PJM 市场机制下［14］，参与调频辅助服务市场的发电商须在14:15 前提交次日全部时段的投标信息，各时段调频辅助服务市场在次日实际运行前60 min关闸，市场关闸前发电商可修改投标信息［17］。调频辅助服务市场的时间框架见附录A图A2。

调频辅助服务市场遵循两部制补偿方法，发电商收益由调频容量补偿、调频里程补偿组成。调频容量是单位投标时段内发电商提供的调频资源之和；调频里程是单位投标时段内发电商根据调频指令上调或下调出力的绝对值之和，反映了调频资源的实际调节量［18］。WCS 在调频辅助服务市场的收益模型为：

式中：Wr，t为t时段WCS 在调频辅助服务市场的预期收益；ccap、cperf分别为调频容量、里程价格；m为平均调频里程；Pr，t为t时段调频辅助服务市场的上报功率；S为t时段快速调频信号的信号值；Tbid为市场投标时段总数。

1.2 偏差-弃风成本和储能寿命折损模型

新能源发电的不确定性导致风电预测出力与实际出力之间总存在一定的偏差，本文将该出力偏差定义为偏差功率。偏差功率的存在导致WCS 无法精准执行上报计划，会使其面临DPWCL。储能在调频辅助服务市场中的计划执行不因偏差功率的存在而受阻，WCS 仅在能量市场中存在DPWCL。WCS的偏差-弃风成本模型为：

式中：Wr，t、Wr，t分别为t时段WCS 所受偏差惩罚、弃风损失；Pr，t、Por，t为t时段WCS 的偏差功率；cL、cH分别为偏差惩罚、弃风损失系数；Pict、P分别为t时段风电的预测、实际出力。

值得说明的是，除了实际运行阶段由偏差功率导致的临时弃风，WCS 的弃风行为还包括投标阶段的计划弃风，则偏差-弃风成本模型中的弃风损失为临时弃风损失。

储能寿命折损与其充、放电电量成正比。WCS上报的调频功率为Pr，t，但在实际运行时，储能并非始终维持该调频功率大小不变，而是随15 min 内均值约为0 且不断变化的调频信号进行充放电。因此，在单位时段Δt内，储能提供调频辅助服务的实际消耗功率为2βPr，t，其中β为单位时段Δt内储能参与调频的实际使用功率与上报功率之比。储能寿命折损模型为：

式中：Wc，t为t时段的储能寿命折损费用；cop为储能寿命折损系数。

2 WCS多时间尺度投标策略

在日前阶段，考虑风电出力的不确定性，以WCS 预期净收益最大为目标制定日前投标策略，确定能量市场的上报功率。

在日内阶段，根据超短期风电预测数据再次对风电出力不确定性进行量化建模，并以此为基础修正储能预留出力能力，调整上报计划中的机组出力。不同阶段的风电预测数据存在偏差，因此须调整能量市场中风电计划调度功率、储能充／放电功率，以适应更新后的风电预测数据。虽然能量市场的上报功率在日前阶段出清后不可改变，但可以在日内阶段重新分配WCS 内部的风电、储能出力，从而减小偏差功率，提高风电消纳率。此外，调频辅助服务市场在日内实际运行前60 min 关闸，发电商可在关闸前修改投标信息［14，17］，且储能的充、放电空间在修正预留出力能力后扩大，WCS 因而可以提高调频辅助服务市场的上报功率以增大经济收益。

多时间尺度投标策略的流程图见附录A图A3。

2.1 基于Copula函数的风电出力不确定性模型

在制定上报计划前，应先基于Copula 函数［19⁃20］构建风电出力不确定性模型，并以此为基础确定储能预留出力能力。预留出力能力不参与能量市场和调频辅助服务市场，仅用于减小突发的偏差功率。

以运行前风电预测出力、运行时风电实际出力的历史数据为样本集，基于核密度估计法分别建立其边缘分布模型。在此基础上，利用最大似然估计法得到Copula 函数的相关系数，从而确定Copula 函数的表达式、风电预测出力与实际出力的联合分布模型。

已知次日风电预测数据（包括日前预测数据、日内超短期预测数据），结合上述边缘分布、联合分布模型，构建次日各时段风电实际出力的条件分布模型。选取合适的置信水平，得到相应的风电实际出力置信区间，即风电出力不确定性区间。对比各时段风电出力不确定性区间的上、下限与预测出力之差的绝对值，选取各时段的最大值作为该时段的储能预留出力能力。

对比不同Copula 函数模型的拟合结果后，本文选取高斯Copula 函数对WCS 进行风电出力不确定性建模。静态Copula 函数的预测精度较低，但其能一次性获得次日全部时段的风电出力不确定性区间；动态Copula函数的预测精度较高，但其只能基于l时段的风电实际出力对l+1 时段的风电出力不确定性进行建模，无法获得剩余时段的风电出力不确定性区间。因此，本文结合日前风电预测出力，在日前投标策略中使用静态高斯Copula 函数，同时结合超短期风电预测出力，在日内投标策略中使用动态Copula函数。

值得说明的是，投标时段间隔Δt=15 min，动态Copula 函数建模时段间隔Δl=60 min。在日内阶段，WCS 基于超短期风电预测数据每隔Δt对Δl后的风电出力不确定性进行建模。

2.2 日前投标策略

根据历史数据和日前风电预测出力，基于静态高斯Copula 函数建立日前风电出力不确定性模型，并设置储能预留出力能力。在日前投标策略中，以WCS 参与能量、调频辅助服务市场的预期净收益最大为目标，确定各时段的风电计划调度功率、储能充／放电功率和调频辅助服务市场上报功率。

2.2.1 目标函数

目标函数可表示为：

式中：W、W、W、W分别为日前投标策略中WCS 在能量市场的预期收益、在调频辅助服务市场的预期收益、计划弃风损失、储能寿命折损费用；P、P分别为t时段日前能量市场的上报功率、日前调频辅助服务市场的上报功率；P、P分别为t时段日前储能的充、放电功率；Pict，da、P分别为t时段日前风电预测出力、风电计划调度功率。

2.2.2 约束条件

1）WCS输出功率约束。

式中：Pmax为WCS的输出功率上限。

2）调频表现约束。

当储能的荷电状态严重偏离中间值时，其无法响应调频信号的充、放电指令，调频服务质量因此下跌。定义分段函数用于评估各时段储能的调频服务质量，取其均值Rda用于衡量储能提供调频服务的综合表现。如果t时段下储能的荷电状态S介于Smax-(Smax-Smin)h和Smax+(Smax-Smin)h之间，表明储能荷电状态未严重偏离中间值，那么R=1；否则，=0.5。其中，h为荷电状态偏离中间值的百分比。则调频表现约束为：

式中：means{⋅}为求取平均值的函数；Rmin为调频表现下限；u为表征t时段WCS 是否参与调频辅助服务市场的0-1变量，若参与则u=1，否则u=0。

此外，还需满足储能的荷电状态约束、运行状态约束、出力约束，分别见附录A式（A1）—（A3）。

2.3 日内投标策略

根据历史数据和日内更新的超短期风电预测出力，WCS 基于动态高斯Copula 函数建立日内风电出力不确定性模型，并基于此修正储能预留出力能力。

在日内投标策略中，以WCS 参与能量、调频辅助服务市场的预期净收益最大为目标，对各时段的风电计划调度功率、储能充／放电功率进行出力再分配，同时调整调频辅助服务市场的上报功率。

储能的充／放电功率存在上限，因此，当日前、日内阶段的风电预测出力差值超过储能功率调节能力时，WCS将无法按照P进行能量市场出力。WCS将在已知该情况的基础上制定日内投标计划，确定能量市场的预期出力P。值得说明的是，能量市场上报功率无法进行修改，仍然为P，因此需要根据P计算能量市场预期收益，并根据能量市场出力差值-计算预期偏差惩罚。

各时段调频辅助服务市场的关闸时刻不同［17］，且WCS 无法基于动态Copula 函数一次性获得剩余全部时段的风电出力不确定性区间，因此分时段对日内投标策略进行优化。

2.3.1 目标函数

目标函数可表示为：

式中：W、W、W、W、W分别为日内投标策略中t时段的WCS 能量市场预期收益、调频辅助服务市场的预期收益、预期偏差惩罚、计划弃风损失、储能寿命折损费用；P为t时段日内调频辅助服务市场的上报功率；Pict，us为t时段超短期风电预测出力；P为t时段日内风电计划调度功率；P、P分别为t时段日内储能的充、放电功率。

2.3.2 约束条件

WCS输出功率约束为：

此外，还需满足储能荷电状态约束、运行状态约束、输出功率约束，分别见附录A式（A4）—（A6）。

2.4 偏差功率带来的成本建模

在实际运行阶段，调用预留储能可降低偏差功率造成的经济损失。但预留储能的出力能力有限，当超出其调节范围时，仍会产生一定的DPWCL，且调用时会产生相应的储能寿命折损费用。

2.4.1 目标函数

目标函数可表示为：

式中：W、W、W分别为实际运行阶段t时段WCS 所受偏差惩罚、临时弃风损失、预留储能的寿命折损费用；P、P为实际运行阶段t时段WCS的偏差功率；P、P分别为实际运行阶段t时段预留储能平抑偏差功率的充、放电功率。

2.4.2 约束条件

预留储能平抑偏差功率的充放电功率约束为：

式中：Pe，t为t时段预留储能的出力能力。

3 算例分析

本文以我国某WCS 作为研究对象，在MATLAB开发环境下进行仿真建模与算例分析，通过Yalmip调用gurobi9.0 求解器进行求解。选取2022 年5 月1日至5 月28 日该WCS 的风电日前预测出力、日内超短期预测出力、实际出力同步测量数据进行分析，每隔15 min 取1 个测量点。价格和设备参数设置参考文献［6，8］，分别见附录B表B1和表B2。

3.1 是否计及风电出力不确定性对WCS 经济性的影响

风电出力的强不确定性会阻碍上报计划的精准执行，因此本文在2.1节对风电出力不确定性进行量化建模，并以此为基础设置预留储能出力能力。预留储能出力能力体现了计及风电出力不确定性对投标决策的影响。

为了验证是否计及风电出力不确定性对WCS经济性的影响，本节设置如下2 种场景：①场景A，WCS 参与能量、调频辅助服务市场，不计及风电出力不确定性；②场景B，WCS 参与能量、调频辅助服务市场，根据日前预测出力构建风电出力不确定性模型，并以此为基础设置预留储能出力能力。2 种场景的收益结果对比如表1 所示。场景A 和场景B的能量市场上报功率、调频辅助服务市场上报功率、偏差功率分别如附录B 图B1 — B3 所示。日前风电出力不确定性区间如附录B图B4所示。

表1 2种场景的收益结果对比Table 1 Comparison of benefit results between two scenarios单位：万元

由图B1 可知：在00:45 — 01:00、09:45 — 12:15、22:00 — 22:15 等时段，场景B 的能量市场上报功率小于场景A 的能量市场上报功率。这是因为预留储能出力能力的设置挤占了储能的放电空间，利用储能提高能量市场上报功率、增加售电收益的行为因此受阻。在01:15 — 01:30、15:00 — 15:15、16:15 —16:30 等时段，场景B 的能量市场上报功率大于场景A 的能量市场上报功率。在这些时段内，储能的放电空间较充足，WCS 增大储能的放电功率以提高能量市场上报功率，从而减小了预留储能出力能力设置对能量市场经济性的负面影响。由表1 可知：相比于场景A，场景B 在全天所有时段的能量市场预期收益减少了0.38 万元。上述分析结果表明，预留储能出力能力降低了WCS在能量市场的经济效益。

同样地，由于预留储能出力能力的设置挤占了储能的充、放电空间，储能的频率调节能力下降，WCS 在调频辅助服务市场的上报功率随之减少，最终导致经济收益显著降低。由图B2 可知：场景B 的调频辅助服务市场上报功率显著小于场景A 的调频辅助服务市场上报功率。由表1 可知：相比于场景A，场景B在全天所有时段的调频辅助服务市场预期收益减少了5.97万元。

由图B3可知：在不设置预留储能出力能力的情况下，所有偏差功率都无法被平抑，WCS 因此承受了高额的弃风损失和偏差惩罚；在设置预留储能出力能力的情况下，大部分的偏差功率能够被平抑，只有少量偏差功率超出了储能的平抑能力。由表1 可知：相比于场景A，场景B 的偏差功率带来的成本减少了11.52万元。上述分析结果表明，预留储能出力能力能显著降低WCS的经济损失。

由表1 可知：相比于场景A，场景B 的净收益增加了4.59 万元，表明预留储能出力能力提高了WCS的实际经济效益。可见，在电力现货市场的投标过程中构建风电出力不确定性模型，并以此为基础设置储能预留出力能力，这样虽然会挤占储能的充、放电空间，从而降低预期净收益，但能平抑偏差功率，进而降低偏差功率带来的成本，最终能够有效提高WCS的经济性。

3.2 不同概率建模方法对WCS经济性的影响

由3.1节可知：预留储能出力能力的设置会影响预期净收益和偏差功率带来的成本，因此需要选择合适的概率建模方法来构建风电出力不确定性模型，并以此为基础设置预留储能出力能力，从而提高WCS的经济性。

为了验证不同概率建模方法对WCS 经济性的影响，本节设置如下3种场景：①场景C，不考虑风电预测出力与实际出力之间的非线性相关性，基于核密度估计法构建风电出力不确定性模型；②场景D，考虑风电预测出力与实际出力之间的非线性相关性，在风电预测出力分层的基础上，采用核密度估计法构建风电出力不确定性模型；③场景E，考虑风电预测出力与实际出力之间的非线性相关性，采用Copula函数构建风电出力不确定性模型。

3 种场景在同一置信度下的风电预测出力与实际出力之间的关系见附录B图B5 — B7，风电实际出力散点分布如表2 所示。从风力发电商的角度出发，风电出力不确定性模型应尽可能地避免实际出力的散点落在置信区间外，并减少区间宽度的冗余，从而在减小DPWCL的同时，降低预留出力能力对储能充、放电空间的挤占程度。因此，本节将着重对比不同场景下置信区间对散点的包裹程度和区间的冗余程度。

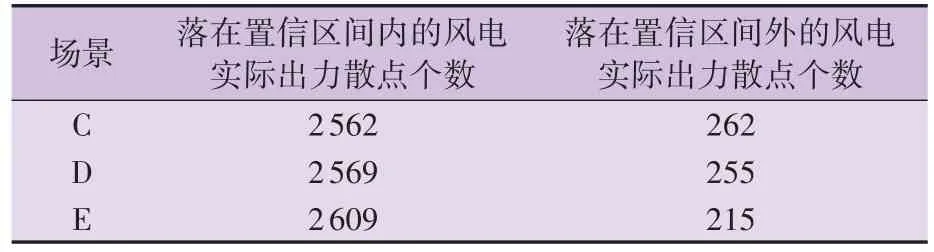
表2 风电实际出力散点分布对比Table 2 Comparison of scatter distribution of actual wind power output

由表2 可知：相比于场景C，场景D 中落在置信区间外的风电实际出力散点相对更少。对比图B5和图B6 可知：在风电预测出力的头部和尾部，场景D 的区间冗余程度相对更低。这是因为风电预测出力与实际出力之间存在非线性相关性，不同预测出力下的实际出力概率分布不同，在不考虑二者相关性的前提下，采用核密度估计法对整体构建概率模型，难以精确描述实际出力的概率分布特征。上述分析结果表明，考虑风电预测出力与实际出力之间的非线性相关性，能够更加有效地反映风电出力的不确定性，从而提升WCS的经济收益。

由表2 可知：相比于场景D，场景E 中落在置信区间外的风电实际出力散点更少；相比于图B6，图B7 中实际出力的置信区间上、下限更贴近其散点分布。这是因为场景D 中功率分层的界限划分存在主观性，而基于Copula 函数构建的风电出力不确定性模型具有自动分层的效果，因此Copula 函数能够更加精确地描述风电实际出力的概率分布特征。上述分析结果表明，基于Copula函数进行概率建模，能够更加有效地反映风电出力的不确定性，从而提升WCS的经济收益。

由此可见，考虑风电预测出力与实际出力之间的非线性相关性，并采用Copula 函数构建风电出力不确定性模型，能够有效提高WCS的经济性。

3.3 多时间尺度市场参与行为对WCS经济性的影响

为了验证多时间尺度市场参与行为对WCS 经济性的影响，本节增设1 种场景：场景F，在场景B 的基础上，WCS 根据日内更新的超短期风电预测数据，构建风电出力不确定性模型，并以此为基础调整预留储能的出力能力、修正日前投标策略。

场景B 和场景F 的预留储能出力能力、偏差功率、调频辅助服务市场上报功率分别见附录B 图B8 — B10。日内风电出力不确定性区间见附录B 图B11。场景B和场景F的收益结果对比如表3所示。

表3 场景B和场景F的收益结果对比Table 3 Comparison of benefit results between Scenario B and Scenario F单位：万元

由图B8可知：相比于场景B，场景F的预留储能出力能力显著减小。这是因为随着时间的推进，风电预测准确性提高，结合风电预测出力数据确定的出力不确定性区间因此减小。由图B3（b）、图B9 和表3 可知：相比于场景B，场景F 中超出预留储能平抑能力的偏差功率减小，因此偏差功率带来的成本降低。上述分析结果表明，考虑日内功率预测准确性的提升，在此基础上构建风电出力不确定模型、降低预留储能出力能力，不会增加WCS的经济损失。

由图B10 可知：在09:45 — 16:30、22:00 — 22:45等时段，场景F 的调频辅助服务市场上报功率显著大于场景B 的调频辅助服务市场上报功率。由表3可知：相比于场景B，场景F 的调频辅助服务市场预期收益提高了3.62 万元，净收益提高了2.44 万元。这是因为储能的充、放电空间因预留出力能力减小而扩大，储能的频率调节能力得到提高，因此WCS可提高调频辅助服务市场上报功率以增加预期收益。上述分析结果表明，在调整预留储能出力能力后，多时间尺度参与电力市场能提高WCS的经济性。

由此可见：结合日内更新的超短期风电预测数据，降低储能的预留出力能力，不会增加WCS 的经济损失；随着预留出力能力的修正，多时间尺度参与电力市场能够提高储能资源的利用效率，进一步提升WCS的经济性。

3.4 考虑风电出力不确定性的WCS 多时间尺度市场参与策略在我国电力市场的有效性分析

本文以美国PJM 市场规则为背景，提出了考虑风电出力不确定性的WCS 多时间尺度市场参与策略。为了验证该策略在我国电力市场中的有效性，本节参照《广东调频辅助服务市场交易规则（试行）》，设置如下2 种场景：①场景G1，WCS 参与能量、调频辅助服务市场，不计及风电出力不确定性，不考虑多时间尺度市场参与机制；②场景G2，WCS参与能量、调频辅助服务市场，根据风电出力不确定性模型设置预留储能出力能力，在日内阶段不改变调频辅助服务市场上报功率，仅修正能量市场中风电和储能的功率分配。2 种场景的收益结果对比见表4。由表4 可知：相比于场景G1，场景G2 的预期净收益减少了8.31 万元，偏差功率带来的成本减少了12.33万元，最终净收益增加了4.02万元。这表明构建风电出力不确定性模型，在此基础上设置预留储能出力能力，并在日内对能量市场中的风电、储能出力进行重新分配，能有效提高WCS的经济收益。

表4 场景G1和场景G2的收益结果对比Table 4 Comparison of benefit results between Scenario G1 and Scenario G2单位：万元

由图B8可知：根据日内更新的超短期风电预测数据构建风电出力不确定性模型，以此为基础调整预留储能出力能力，能够扩大储能的充、放电空间。但在我国电力市场的现行规则下，WCS 无法在日内改变调频辅助服务市场上报功率，进而提高调频辅助服务市场的经济收益。因此，多时间尺度市场参与机制对WCS经济性的提升存在局限性。

可见，在当前我国的电力市场背景下，本文所提考虑风电出力不确定性的WCS 多时间尺度市场参与策略能够有效提高WCS 的经济收益，但其优越性还不能完全体现。美国PJM 市场发展较早、较为成熟，可为我国电力市场未来的构建、发展提供经验和启示。随着我国电力市场机制的不断完善，本文所提策略的优势将日益凸显。

4 结论

针对风电强不确定性导致的电力市场投标偏差问题，本文参考美国PJM 市场机制，建立了风电出力不确定性模型，以此为基础设置了预留储能出力能力，并跟随风电预测数据的更新调整投标决策，提出了考虑风电出力不确定性的WCS 多时间尺度市场参与策略。基于算例结果可得如下结论：

1）基于Copula 函数建立风电出力不确定性模型，确定预留储能出力能力，这样虽然会相对降低预期收益，但能显著减小DPWCL，从而可有效提升WCS的实际收益；

2）考虑风电预测出力与实际出力之间的非线性相关性，并采用Copula 函数构建风电出力不确定性模型，能够有效提高WCS的经济性；

3）多时间尺度市场参与策略能够提高储能资源的利用效率，进一步提升WCS的经济性；

4）在当前我国的电力市场背景下，本文所提策略的优越性暂时还不能完全体现，但随着我国电力市场机制的不断完善，其优势将日益凸显。

附录见本刊网络版（http：//www.epae.cn）。