基于涟漪扩散算法的应急疏散路径优化方法研究

胡小兵，袁莉燕，李航，赵宇勃，张勇，李奇轩

(1.中国民航大学，a.体系安全与智能决策实验室，b.电子信息与自动化学院，c.中欧航空工程师学院，天津 300300；2.河北省高速公路京雄筹建处，河北保定 071000)

0 引言

随着社会经济的快速发展，商场、景点、高铁站及机场等大型公共场所的数量急剧增加，这些场所承载的人员密度极大，当火灾、地震、危险品爆炸等突发公共安全事件发生时，疏散人员会盲目选择当下距离出口最近的路线，极易造成路网中的拥堵现象，导致人员疏散不及时，引发一系列严重后果。因此，研究路网中疏散路径优化策略，给出一套准确且高效的应急疏散方案对于提高路网中人群疏散效率，减少人员伤亡和财产损失具有重要意义。

处理路网中人群应急疏散问题的关键在于疏散路径优化，应急疏散路径优化问题是一个典型的NP-hard问题[1]。目前，求解该问题的方法主要分为两类。

一类是聚焦微观层面的模拟仿真类方法，该类方法通过建立微观模型，突出刻画疏散人员在受到多种因素影响时产生的个体行为，以此来确定最优疏散路径。常见微观模型主要有元胞自动机模型(Cellular Automata,CA)[2]、社会力模型(Social Force Model,SFM)[3]和格子气模型(Lattice Gas Model,LGM)[4]。模拟仿真类方法能更细致地反映疏散人员的状态，但同时也会增加求解复杂度，使得求解时间较长。

另一类方法是聚焦宏观层面的智能优化类方法，该类方法从全局角度为疏散人员分配最优路径，以期提高整体的疏散效率。Zhao等[5]提出一种新的出口评估策略，结合人工蜂群算法进行疏散路径优化。Huang等[6]在蚁群算法中引入增量流量分配方法(Incremental Flow Assignment,IFA)来实现路径优化，提高人群疏散效率。Liu等[7]提出一种改进的多路线人工鱼群算法，解决邮轮上的多路线疏散路径优化问题。刘涛[8]基于改进蚁群算法构建疏散路径优化策略，处理结构较为复杂的多层建筑中的人群疏散。这类启发式算法参数较多，在求解时易陷入局部最优，较难保证解的质量。罗茂颖[9]对Dijkstra 算法进行了数据储存优化和堆优化，求解特定节点到各安全出口的距离最短路径。Li等[10]使用障碍物的顶点来构建路径节点，并综合考虑了节点的安全性，求解出最短路径。上述研究都以寻找距离最短路径为目标，频繁求解得出最短路径容易造成疏散时路网中的拥堵，延长疏散时间。张明空等[11]提出一种协同进化路径优化方法，实现了动态火灾情景下应急疏散路径的动态优化，有效提高了高层建筑的疏散效果，但该方法只考虑了具有单起点单终点的路网场景。

综上所述，本文提出一种考虑容量限制的多起点多终点涟漪扩散算法(Capacity Constrained Ripple Spreading Algorithm,CCRSA)。该算法综合考虑路径容量限制与具有多起点多终点路网的人群流量分配情况，计算得出各起点的全局疏散时间最短路径，动态更新路网中各链接在各时刻的剩余最大通行容量，并根据路径寻优规则来确定最优疏散路径，实行差异化疏散，有效提高路网中人群疏散效率，优化应急疏散方案。

1 问题描述

在进行人群疏散路径优化时，需要考虑路径容量限制等一系列约束条件，在保证安全性的前提下，为某一场所内分布在不同位置的所有人员合理安排疏散时间点、优化疏散路径，使得在最短时间内所有人都能够到达安全出口。

由于在实际路网的人群疏散过程中，疏散情况较为复杂，故本文做如下假设：

(1) 疏散路网存在多个起点和多个安全出口，疏散开始时，每名待疏散人员随机分布于各个起点；

(2)疏散路网中的链接等效于实际道路，具有一定的单位时间通行容量上限，且容量上限的大小取决于每条链接的宽度；

(3)疏散人员在各条链接上具有一定的移动速度，即每条链接的通行时间为常数；

(4)疏散过程中允许疏散人员在路网的节点处等待。

图1展示了不同方案路径选择对比，各链接的属性以(x,y)表示，其中，x表示该链接的单位时间最大通行容量，y表示该链接的通行时间，假设初始时刻起点5 的待疏散人数为10 人。若所有人员均选择起点到终点的距离最短路径[5,4,3]进行疏散，10人全部疏散用时7 s，产生的等待时间为4 s；而优化后疏散路径为2 人选择路径[5,4,3]，3 人选择路径[5,0]，3 人选择路径[5,2,3]，2 人等待1 s 后选择路径[5,4,3]，则10 人全部疏散只需用时5 s，产生的等待时间只有1 s。所使用的符号和决策变量如表1所示。

表1 使用的变量符号说明Table 1 Description of variables and symbols

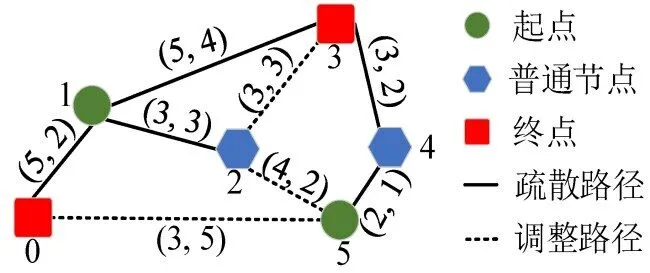
图1 路径选择方案对比Fig.1 Comparison of path selection schemes

1.1 路网建模

构建人群疏散路网模型。给定一个路网G(N,E)由节点集合N和链接集合E组成。节点集合N包含起点即待疏散人员所在节点集合Ns={sk},k∈{1,2,…,o}，普通中间节点集合Nu={uk},k∈{1,2,…,q}，终点即安全出口集合Nd={dk},k∈{1,2,…,z} 。链接集合E={eij|i∈N,j∈N} 囊括了所有相连节点间的链接，其中，eij为节点i和节点j之间的链接，表示实际可通行的路径，则相邻节点对集合可表示为V={(i,j)|eij∈E} 。使用邻接矩阵A来构建实际路网，即

其中，若lij>0，则表示路网中节点i与节点j间的链接eij的长度为lij；若lij=0，则表示节点i和节点j之间不存在链接，无实际通行道路。此外，A(i,i)=0，即任意节点i与自身不存在相连的链接。

疏散人员在链接eij上的移动速度为vij，则链接eij的通行时间为

使用式(2)计算得到各链接的通行时间，并构成以通行时间为权值的邻接矩阵T，即

路网中的任意链接都存在单位时间内允许通行的人数上限，链接eij的最大通行容量为cij，则最大通行容量邻接矩阵C可表示为

1.2 优化目标

优化目标为最小化路网中所有待疏散人员的清空时间，即最小化路网中最后一位待疏散人员到达安全出口的时间。优化目标可描述为

1.3 约束条件

式(6)表示在初始时刻路网在各中间节点和终点的疏散人员数量为0。式(7)和式(8)分别表示在初始时刻位于各链接、各终点的疏散人员数量为0。式(9)表示在任意时刻t各链接的疏散人员数量都不得超过该链接当前的剩余最大通行容量。式(10)表示通过任意节点的疏散人员数量守恒。式(11)表示在任意时刻t从每个起点出发的疏散人员数量守恒。式(12)表示疏散人员总人数守恒，即初始时刻各起点的疏散人员数量总和等于疏散结束时位于各终点的疏散人员数量总和。式(13)表示若来自起点sk的疏散人员m在t时刻位于链接(i,j)，则决策变量，否则

2 求解算法

针对应急疏散路径优化问题，设立人员移动规则、人员等待规则与路径寻优规则，提出考虑容量限制的多起点多终点涟漪扩散算法(CCRSA)。

2.1 疏散规则

2.1.1 人员移动规则

疏散人员在链接上移动时，遵守先进先出(First-in-first-out，FIFO)规则。如图2 所示，feva(t,1)和feva(t,2)表示在t时刻位于链接eij上的两组疏散人员，第1 组疏散人员feva(t,1)经过Δt时间后由位置(2)移动到位置(4)，第2 组疏散人员feva(t,2)经过Δt时间后由位置(1)移动到位置(3)。在移动过程中，第2组疏散人员始终排在第1 组疏散人员的后面。

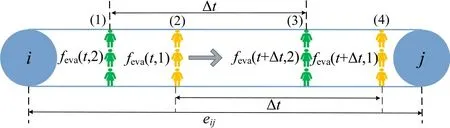
图2 单条链接人员移动规则Fig.2 Movement rule of evacuees on single link

当多条链接交汇时，疏散人员的移动同样遵循FIFO 移动规则。如图3 所示，链接es1u3和链接es2u3在节点u3处交汇，并与链接eu3d4相连。其中各链接中矩阵的列数表示该链接的通行时间长度，譬如es1u3的矩阵有两列，表示通过该链接需要2 s；矩阵的行数表示该链接的最大通行容量，es1u3的矩阵有一行，则表示其最大单位时间通行容量为1；矩阵中的元素表示在当前时刻该位置是否有疏散人员，1表示有，0 表示没有。t=1 时有1 名疏散人员从链接es1u3运动至链接eu3d4，又有两名疏散人员从链接es2u3运动至链接eu3d4，则t=1时共有3名疏散人员到达链接eu3d4。同理，t=2 时共有1 名新的疏散人员到达链接eu3d4。

图3 链接交汇人员移动规则Fig.3 Movement rule of evacuees at link crossover

2.1.2 人员等待规则

Adrian等[12]归纳出，在出现突发情况时，人群易激发自我心理，盲目寻找距出口最近的疏散路线，这样反而会导致路网中产生大面积拥堵，延长疏散时间，出现“快即是慢”的效应。因此，为充分利用每条疏散路线，更好地缓解疏散时的拥堵，为疏散人员在路网中的节点处增加等待行为，可以有效减少整个路网中所有疏散人员的清空时间。

疏散人员在节点i处的等待时间ti,wait可以描述为

疏散人员在规划好的疏散路径ps上通行时，其疏散时间Hs可描述为

2.1.3 路径寻优规则

随着疏散的进行，路网中各链接各时刻的剩余最大通行容量不断更新。通过考虑每条链接的通行时间，以及其在疏散人员到达该链接时的剩余最大通行容量，来设置路径寻优规则，确定优先疏散路径，路径寻优的评价标准为

式(16)中分子为疏散人员在路径ps的疏散时间Hs，分母为组成路径ps的各链接在疏散人员到达时的剩余最大通行容量与起点待疏散人数中的最小值。该比值最小的路径为优先疏散路径。

2.2 CCRSA

2.2.1 多对多RSA

涟漪扩散算法(Ripple-spreadingAlgorithm,RSA)的提出是受到自然界中涟漪扩散现象的启发。其路径搜索过程是模拟涟漪在水面上向四周以相同速度扩散，它总是最先到达距涟漪中心最近的节点。当涟漪触碰到障碍物即新的节点时，又会触发新的涟漪继续扩散。因此其路径搜索过程可以形象地描述为路网中各个节点间的涟漪接力赛。

多对多涟漪扩散算法原理如图4 所示，t=1时，起点1和起点5分别产生涟漪R1和R2，在路网中开始扩散；t=2 时，R2到达节点4，并在节点4处激发新的涟漪R3；t=3 时，R1到达终点0，通过回溯找到起点1到达终点的最短路径[1,0]，该涟漪消亡；t=4 时，R3到达终点3，通过回溯找到起点5到达终点的最短路径[5,4,3]，所有涟漪消亡。

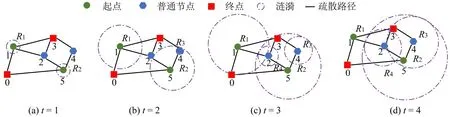
图4 多对多涟漪扩散算法原理Fig.4 Principle of many-to-many RSA

2.2.2 CCRSA求解流程

RSA 在路径优化方面的优势已经得到证明[13]。结合2.1 节所设置的疏散规则，提出CCRSA，动态更新路网中各链接在各时刻的剩余最大通行容量，容量不足时添加涟漪在节点的等待行为，将等待时间考虑在内，一次性计算出多个起点到多个终点的疏散时间最短路径；并使用路径寻优规则确定优先疏散路径，分配疏散人员数量，实行差异化疏散，提高路网中各链接的利用率。

CCRSA 使用的符号说明如表2 所示，CCRSA伪代码如表3所示。

表2 CCRSA符号说明Table 2 Description of symbols in CCRSA

表3 CCRSA求解流程Table 3 Working flow of CCRSA

CCRSA的求解流程如下。

Step 1 初始化路网，给定各起点sk的待疏散人数(0)、各链接的最大通行容量C和各链接的通行时间T。

Step 2 判断各起点是否存在未疏散人员，若不存在，则算法运行终止；若存在，则算法继续运行，即表3第1行。

Step 3 初始化各涟漪状态，设置涟漪的扩散速度，即表3第2～4行。

Step 4 判断各起点的涟漪是否都通过涟漪接力赛到达终点，若是，则转至Step 10；否则，转至Step 5，即表3第5行。

Step 5 涟漪状态更新，对处于等待状态涟漪，当与其中心点相连的某一链接当前剩余最大容量满足Xij(t)>0 时，涟漪在该方向上由等待状态变为激活状态，并记录等待时间ti,wait，即表3第7～11行。

Step 6 所有激活状态的涟漪以速度v开始扩散，即表3第12行。

Step 7 对于所有处于激活状态的涟漪，判断是否到达其中心节点的相邻节点。若是，则在相邻节点处触发新的涟漪，并更新到达节点时间，即表3第13～16行。

Step 8 根据各链接的剩余最大容量，判断新涟漪在各方向上的状态，即表3第17～23行。

Step 9 当涟漪已到达其中心节点的所有相邻节点后，涟漪消亡，即表3第24～26行。

Step 10 根据路径寻优规则，确定优先疏散路径ps，并确定本次疏散人员数量fs，即表3 第28行。

Step 11 根据本次疏散人员数量和到达各节点的时间，更新各链接在对应时刻的剩余最大容量和起点待疏散人数，即表3第30行。

Step 12 本次疏散结束，开启下一轮疏散时间最优路径搜索，直至各起点所有人员都被疏散至终点，输出Pfin,Ffin,Hend。

3 实验分析

本节使用大量的随机生成路网对算法进行测试，并将CCRSA 的实验结果与多路径容量约束规划算法(Multiple-Route Capacity Constrained Planner,MRCCP)、遗传算法(Genetic Algorithms,GA)的实验结果进行对比分析。此外，使用一个实际案例来证明CCRSA 的应用价值。所有算法和测试均使用Python3.9 编程实现，并以配置 为Windows10，Intel(R) Core(TM) i7-9700CPU，3 GHz，16.0 GB RAM 的计算机作为实验平台，开展对比实验。

设置3 个评价指标ET、RT、Std。ET 表示路网中所有待疏散人员全部到达安全出口所需的时间，即清空时间(s)；RT 表示程序运行时间(s)；Std 表示每名疏散人员到达出口的实际时间与理想时间的标准差。每名疏散人员都希望在最短时间内到达安全出口，故将其理想疏散时间设置为在不考虑等待时间的情况下所在起点到终点的最短路径通行时间。标准差计算公式为

式中：m为第m个待疏散人员；tm,act为疏散人员m到达终点的实际时间；tm,ide为疏散人员m到达终点的理想时间。标准差Std 越小，表明疏散时间越符合疏散人员的心理预期。

在进行每次对比实验时，为了保证实验结果的准确性，对于每一个算例，都将GA 运行300 次，从300次实验结果中取出ET、RT与Std的最小值记为对于本算例GA的最优解，即GA_Best。

3.1 随机路网对比实验

使用NetworkX 生成4 组具有不同节点数量的路网，其中每组路网共包括10 个节点数量相同的随机路网，每组路网中各链接的长度与最大通行容量都具有相同数量级。对每个路网都分配4 次不同数量的疏散人员进行实验，每次实验的待疏散人员数量以节点数量的整数倍形式依次递增。具体路网参数设置如表4 所示。对每组路网中10 个算例的实验结果取平均值，对比实验结果如表5所示。

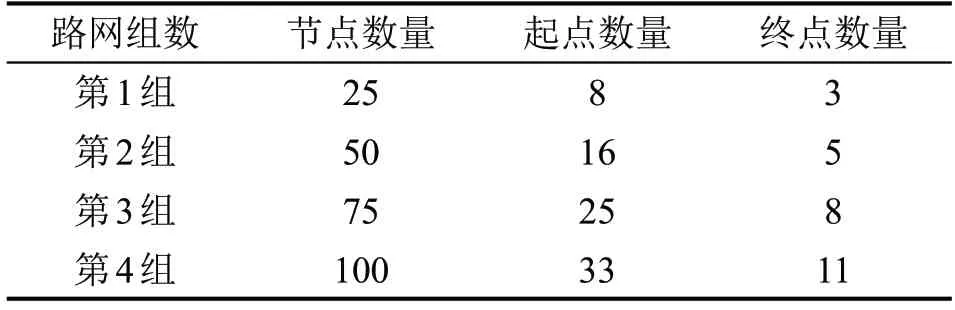
表4 路网参数设置Table 4 Setting of road network parameters

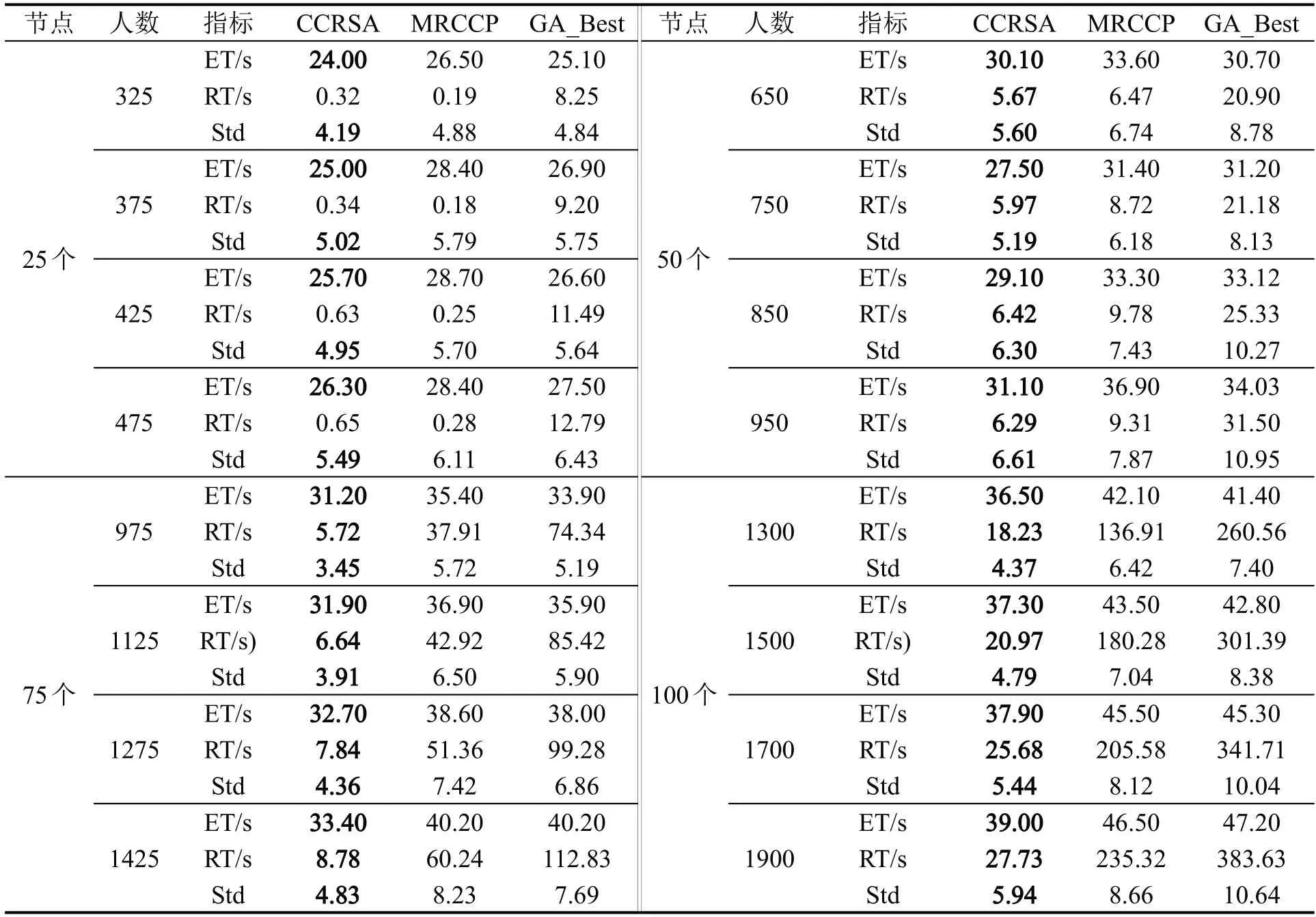
表5 对比实验结果Table 5 Result of comparative experiments

由表5实验数据进行分析可得以下结论：

(1)从4组实验结果整体来看，在具有相同节点数量的路网中，对于不同数量的待疏散人员，CCRSA 的疏散时间ET 均为3 种算法中的最小值。且相较于MRCCP和GA，CCRSA在疏散时间ET方面性能的提升随着路网节点数量的不断增多而逐渐增大。如表6 所示，分别与MRCCP 和GA_Best相比，在路网节点数量分别多于25与50时，CCRSA在减少疏散时间方面性能的提升可超过10%。由此可见，随着待疏散人员增多与路网规模增大，CCRSA在减少疏散时间方面的效果愈发明显。

表6 CCRSA对ET的提升效果Table 6 Improvement effect of CCRSA on ET

(2)4 种不同规模的路网中对于不同数量的待疏散人员，实验结果中CCRSA 的标准差Std 均为3 种算法中的最小值。且标准差值较为稳定，并未随着路网节点数量的增加而明显上升，故表明使用CCRSA优化得到的疏散路径更加符合待疏散人员的心理预期，可以较好地满足各疏散人员在期望时间内快速疏散至安全出口的实际需求。

(3)当路网节点数量大于25 时，相较于其他两种算法，CCRSA 具有更短的程序运行时间RT。且CCRSA 相对于其他两种算法运行效率的提升，随着待疏散人数的增多与路网节点数量的增加而逐渐增大。以第4 组具有100 个节点的路网、1900 名待疏散人员的实验结果为例，相较于MRCCP 与GA_BEST，CCRSA的运行效率分别提升88.21%与92.77%。原因在于RSA与大多数确定性自上而下的集中式路径优化方法(如Dijkstra算法)不同，RSA是一种自下而上的基于微观智体的算法，在寻路过程中不需要计算比较从起点到中间节点的路径时间长度，而是模拟涟漪在路网中传播和在节点处激活新涟漪的行为，因此在处理大规模路网的人群疏散问题时，在计算效率方面具有更明显的优势。

3.2 实际路网对比实验

选取北京市著名旅游景点颐和园作为实际案例验证算法的实际应用价值。颐和园作为大型公共场所，人员分布较为密集，亟需制定应对突发情况的人群应急疏散方案。2023年4月12日，颐和园10:00 实时在园人数达15000 人，15:00 实时在园人数达到35000 人。图5(a)为颐和园全景路网图，图5(b)为颐和园的四大部洲及万寿山景区附近，地形较为复杂，该部分路网共包含65 个节点。根据实时在园人数数据，设置5 组实验，待疏散人数分别为700，900，1100，1300，1500 人，待疏散人员随机分布在26 个起点，并设置4 个终点即安全出口，测试路网及人员分布如图5(b)所示。对CCRSA、MRCCP、GA 开展对比实验，分析结果。实验结果如图6所示。

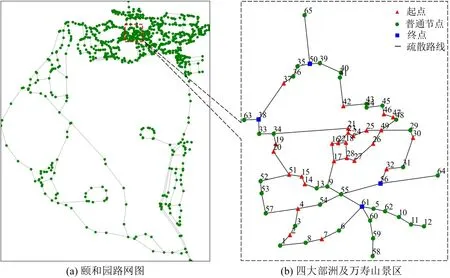
图5 实际案例分析路网图Fig.5 Road network of case study

图6 实际案例对比实验结果Fig.6 Result of comparative experiments on case study

图6(a)为3种算法疏散时间的对比情况，可以看出，对于不同数量的待疏散人员，使用CCRSA均可获得更短的疏散时间。针对5组不同数量待疏散人员的分布情况，相较于MRCCP，CCRSA分别减少了11.81%、11.21%、11.36%、14.38%、15.52%的疏散时间，相较于GA_BEST，CCRSA分别减少了20.49%、24.26%、26.41%、27.62%、28.29%的疏散时间。

图6(b)对比了3种算法的标准差。针对5组不同数量待疏散人员的分布情况，CCRSA 的标准差均为3种算法中的最小值，CCRSA求解得出的疏散方案更加贴合各疏散人员的期望。

图6(c)对比了3 种算法的程序运行时间。5 组实验中，CCRSA的运行效率较高，且在其他两种算法的程序运行时间随人数增加而快速增长的情况下，CCRSA 运行时间的增长幅度较小，为3 种算法中的最小值，较为稳定。

通过对此实际案例的分析，证明了CCRSA 在实际路网环境中具有一定的实际应用价值。

4 结论

本文得到的主要结论如下：

(1) CCRSA 为路网中的人群提供疏散路径优化策略，提高了路网中各链接的利用率，实现了差异化疏散，可以有效减少人群疏散时间。与传统算法相比，CCRSA 平均可减少13.07%的人群疏散时间，且所得疏散方案中各疏散人员的实际疏散时间更为贴近其自身的期望值。

(2) 随机实验和颐和园实际案例分析表明，CCRSA 的运行效率较高且较为稳定，其程序运行时间不会随着疏散人员的增多与路网规模的扩大而显著增长，并且CCRSA 在运行效率方面的优势会随着路网规模的增大、疏散人员的增多而更加明显。CCRSA较适用于大规模路网的应急疏散路径优化。