外卖配送电动自行车换电柜选址定容实证研究
孙小慧,黄诚允
(1.新疆大学,建筑工程学院,乌鲁木齐 830017;2.新疆大学,商学院,乌鲁木齐 830091)
0 引言
随着生活节奏的加快以及人们对便捷和高效的消费需求的增加,外卖逐渐成为人们日常生活中不可或缺的一部分,同时,人们对于外卖配送时效的要求也越来越高。电动自行车因体积小、便利、骑行成本低及低碳环保的特点成为外卖配送交通工具的首选,作为即时外卖配送服务重要保障设施的换电柜应运而生。然而,当前外卖配送电动自行车换电柜的建设主要凭借主观经验确定,不合理的布局造成部分换电柜利用率低,部分换电需求得不到及时满足的供需矛盾现象,从而带来换电柜建设成本高,但用户满意度低的问题,严重影响外卖配送业务的服务质量及行业发展。因此,研究外卖配送电动自行车换电柜的布局建设显得尤为重要。
目前,专门针对电动自行车换电柜布局的相关研究极为缺乏,帅春燕等[1]基于某大型换电企业在四川成都40 d的电动自行车换电订单数据,提出基于整合移动平均自回归(ARIMA)模型的区域换电需求预测方法,结果表明,换电订单在时序上具有很强的线性和周期性特征,换电订单量受到短期订单量的影响更大,且短期内的变化具有平稳性。此外,帅春燕等[2]还基于国内某大型换电企业在成都、无锡、武汉及北京4座城市的换电数据、POI 数据和成都市的部分外卖需求数据,使用线性回归分析方法和K-means聚类算法,研究换电柜的换电订单需求与周边POI密度之间的关系,并据此提出电动自行车换电柜的选址策略,但该研究仅从换电柜覆盖外卖需求的视角进行换电柜的选址,未考虑外卖骑手配送路径,且未建立相关选址优化模型确定站点规模及容量。
电动自行车换电柜选址与电动汽车充换电设施选址同属于服务设施选址问题,电动汽车充换电设施选址相关研究可为电动自行车换电柜选址提供有益的借鉴。目前,电动汽车充换电设施选址研究通常是在预测充换电需求的基础上,建立充换电设施布局优化模型,从备选设施站点中选取最优的站点组合。充换电需求预测作为充换电设施布局的前提,通常利用电动汽车出行数据,通过统计或模拟的方法挖掘电动汽车的出行时空分布特征,进而预测所研究区域充电需求的时空分布。例如,杨珍珍等[3]基于海量移动位置数据,采用网格化的交通需求量统计方法挖掘潜在的交通需求分布位置;HU等[4]从GPS(Global Positioning System)数据中提取寻找和充电与行驶子轨迹,将研究区域离散网格化,并以网格单位识别充电出行需求;周筝等[5]采用基于时空统计量的方法挖掘电动汽车出行数据的时空分布特征,结合电动汽车的出行与充电行为构建充电需求预测模型,获得区域内充电需求时空分布;李映炼[6]根据电动汽车出行时间和空间特征量的概率密度函数,利用蒙特卡洛方法模拟电动汽车一天的出行和充电决策过程,得到电动汽车充电需求的时空分布;DOMINGUEZ等[7]通过建立电动汽车到达和充电过程模型,采用蒙特卡洛方法模拟充电需求;LIN等[8]提出一种基于智能体的出行链模型,模拟电动汽车的行驶和充电模式,预测充电需求的时空分布。充换电设施布局优化模型的建立旨在构建目标函数,并在一定的约束条件下求得最优的服务设施位置和容量,目标函数的构建通常兼顾运营商和用户双方利益。例如,张宇[9]建立以充电站总成本和用户充电总成本最小为优化目标的充电站选址定容模型,并采用遗传算法求解模型;张智禹等[10]建立以充电站年均建设成本、运营成本、惩罚成本以及充电成本最小为优化目标的充电站选址定容模型,并基于改进粒子群优化算法求解模型;ZHANG等[11]建立一个多目标双层规划模型,上层模型以最小化总建设成本和最小化用户总服务延迟时间为目标,确定充电站的位置和容量,下层模型以最小化总出行时间为目标,确定充电站的用户分配。
电动自行车与电动汽车虽在能源补给和充换电设施配置方面有一定的相似之处,但由于外卖配送电动自行车和电动汽车的出行特点不同,充换电需求的时空分布规律存在差异,同时,外卖配送电动自行车换电柜和电动汽车充换电设施的备选站点因规模不同也存在较大差异,电动汽车充换电设施布局相关研究成果能否适用于外卖配送电动自行车换电柜布局实践,仍需进行深入分析。
因此,本文针对外卖配送电动自行车换电柜建设理论与实践存在的问题,通过借鉴电动汽车充换电设施选址相关研究成果,基于外卖配送电动自行车出行行为特点分析,预测换电需求的时空分布,进而综合考虑运营商和用户利益开展换电柜选址定容研究,为换电柜运营商提供一定的决策参考。
1 外卖配送电动自行车换电需求预测
准确预测换电需求是合理布局换电柜和投放电池量的必要前提。根据外卖订单数据预测电动自行车换电需求和换电柜选址定容最为合理,然而,由于商业壁垒的存在,订单数据往往难以获取;相关研究表明,在外卖需求数据难以获取的情况下,使用可能产生外卖需求的POI数据可获得较好的换电需求预测结果[2]。因此,本文使用POI数据,基于仿真模拟预测外卖配送电动自行车的换电需求。
1.1 基于POI数据的外卖配送起止点确定
根据文献[2],本文通过将餐饮名称设为起点关键词,小区、公司、学校、医院及商场等地点名称设为止点关键词,采用Python编程获取城市可能产生外卖需求的POI 数据。数据字段信息包括POI 具体名称、类别、经度及纬度等。
由于POI 数据规模大,为方便后续计算,需要先对POI 数据进行聚类,本文采用K-means 聚类算法实现POI数据的聚类分析。K-means聚类算法的核心思想是把POI数据点划分成K个聚类,聚类的判别准则是使每个聚类中的POI 数据点到该聚类质心的距离最小,划分的处理过程如下:
Step 1 从全部POI 数据点中任意选取K个对象作为初始聚类质心。
Step 2 计算每个POI 数据点到各个聚类质心的欧式距离,将与初始聚类质心欧式距离最近的POI数据点分配到同一个聚类中。
Step 3 待所有POI数据点分配完毕后,重新计算K个聚类的质心。
Step 4 将重新得到的K个聚类结果与上一次的结果相比较,如果发生变化,则转Step 2。
Step 5 重复Step 2~Step 4,直至聚类结果不再变化。
Step 6 输出聚类结果,得到外卖配送起止点。
1.2 外卖配送电动自行车换电需求仿真预测模型假设
本文在已有研究的基础上进行拓展,通过考虑外卖骑手配送路径预测外卖配送电动自行车换电需求。由于外卖订单数据难以获取,外卖配送路径更是未知,为便于仿真预测换电需求,本文做如下假设。
(1)假设所有的外卖配送电动自行车均为同一种型号,车辆的耗电量和换电技术要求完全一致。
(2)根据实际调研,目前,大部分骑手会选择在最后1次外卖配送结束时进行1次换电,以便于第2天的正常外卖配送,因此,假设骑手从家出发时的电池电量为100%。
(3)考虑外卖配送电动自行车的特点和外卖配送时效性的要求,假设外卖配送路径为起止点间的最短路径,且行驶速度仅与车辆性能和交通法规有关,不受交通状况的影响。
(4)假设换电策略为:当电动自行车的电池剩余电量低于某一值时,则需立即进行换电;反之,则不需要换电,不考虑换电市场竞争状况和换电柜信息化服务水平的影响。
1.3 基于仿真模拟的外卖配送电动自行车换电需求预测
基于聚类得到的外卖配送起止点和外卖配送最短路径等假设,通过构建交通路网,模拟骑手一天的外卖配送出行行为,进而预测换电需求的时空分布,即模拟骑手从家(居住地)出发,经过接收订单到赶往配送起点,再到配送终点,不断重复配送活动,最后,返回家(居住地)的过程。具体流程如下:
Step 1 初始化相关参数
Step 1.1 初始化各外卖配送起止点位置和起止点间的距离,基于聚类的外卖配送起止点确定位置坐标,并基于交通路网计算起止点间的最短距离。
Step 1.2 初始化外卖配送出行OD,基于聚类的外卖配送起止点,以及换电订单数据和部分外卖订单数据随机生成OD矩阵。
Step 1.3 初始化外卖骑手首次从家出发时刻,根据换电订单数据和部分外卖订单数据给出外卖骑手从家出发时刻服从的分布,据此生成所有外卖骑手首次从家出发时刻。
Step 1.4 初始化电动自行车电池剩余电量为100%。
Step 1.5 初始化外卖骑手居住地位置,随机选取路网节点作为外卖骑手居住地。
Step 1.6 初始化电动自行车换电阈值,若电动自行车的电池剩余电量低于此值则需立即进行换电;反之,则不需要换电。
Step 1.7 初始化仿真环境,根据实际调研,设定配送时间段,并将其作为仿真时长;此外,根据精度需要设置骑手一天的外卖配送出行行为模拟迭代次数。
Step 2 判断电动自行车位置和电池剩余电量,做出换电决策
Step 2.1 电动自行车电池剩余电量根据行驶距离和耗电量确定。基于电动自行车行驶1 km所耗的电量,以及外卖配送起止点间的最短距离,计算电动自行车的电池剩余电量数据,并记录电动自行车电池剩余电量小于换电阈值时的车辆位置。
Step 2.2 判断电动自行车的电池剩余电量,做出是否换电的决策。若电动自行车电池剩余电量低于换电阈值,则车辆需前往最近的换电柜进行换电。
Step 3 仿真结束
基于仿真结果得到各需求点换电需求量所占比例,然后,根据换电订单预测数据计算各个需求点换电需求量的数值,得出换电需求的时空分布。
2 外卖配送电动自行车换电柜选址定容模型构建
外卖配送电动自行车换电柜的选址定容涉及运营商和用户两个主体的利益,因此,本文根据已有研究成果,同时,从运营商和用户的角度出发,建立以建设成本、运营成本及惩罚成本最小,用户满意度最高的多目标优化模型。
2.1 目标函数
模型目标函数包括最小化换电柜运营商的建设成本、运营成本和惩罚成本,最大化用户满意度。
(1)建设成本
换电柜的建设成本主要包含换电柜柜体购置成本、电池成本和土地成本,即
式中:C1为换电柜年均建设成本;J为换电柜候选点集合,J={1,2,…,j,…};xjk为0-1决策变量,若j点建立等级为k的换电柜,xjk为1,若j点未建换电柜,xjk为0;k为换电柜等级,k∈{1,2,3},同级别换电柜中电池的数量相等,且2 级和3 级换电柜中电池数量分别是1级换电柜中电池数量的2 倍和3 倍;Bjk为j点所建等级为k的换电柜的柜体成本;Ajk为j点所建等级为k的换电柜的占地面积;Rj为j点所在区域每平方米的平均租金;E为换电柜中每块锂电池成本;Qjk为j点所建等级为k的换电柜中电池数量;r为贴现率;T1为换电柜运营年限;T2为电池使用年限。
(2)运营成本
换电柜的运营成本主要是换电柜建设完成后正常运转供用户进行换电产生的相关成本,主要包括设备维护成本和电力成本,即
式中:C2为换电柜年运营成本;Ojk为j点所建等级为k的换电柜的年设备维护成本;Ejk为j点所建等级为k的换电柜的年电力成本。
(3)惩罚成本
服务设施常因容量限制问题导致不能满足需求,从而带来一定的运营损失,本文借鉴已有研究中关于惩罚成本的定义,在运营商成本中考虑需求惩罚成本,即当换电柜服务范围内的换电需求没有足够的可用电池满足时所导致的损失成本,即
式中:C3为惩罚成本;I为换电需求点集合,I={1,2,…,i,…};Pij为换电需求i在j点的惩罚成本;yij为0-1决策变量,若换电需求i前往换电柜j换电,yij为1,否则为0;λ为需求惩罚系数;lj为j点的换电需求量。
(4)用户满意度
已有充换电设施选址相关研究通常基于接受服务的时间和距离考虑用户的满意度,因换电时间较短,本文的用户满意度只考虑距离满意度,即
式中:S为用户对距离满意度的均值;Ld和Ud分别为用户对距离满意度变化的临界值的下限和上限;dij为需求点i到换电柜j的距离;F(dij)为换电需求i在j点的用户换电满意度值。F(dij)与dij的关系如下:
(1)dij在区间[0,Ld] 时,用户满意度最高为1;
(2)dij在区间(Ld,Ud]时,用户满意度为(0,1)区间的数值,在此区间内,用户对距离的满意度随着距离的增加而降低;
(3)dij在区间(Ud,∞)时,用户满意度最低为0。
2.2 约束条件
式(7)表示1个换电需求只可被1个换电柜提供服务;式(8)表示只有布设的换电柜才能为外卖骑手提供服务;式(9)表示布设的换电柜应至少为1个换电需求提供服务;式(10)表示换电柜服务的换电需求量要满足换电柜的容量约束;式(11)和式(12)表示决策变量的取值约束。
3 案例分析
为验证外卖配送电动自行车换电需求预测方法和换电柜选址定容模型的有效性,本文以新乡市主城区为例,应用上述方法和模型得出该区域的外卖配送电动自行车换电柜选址定容最优方案,并对其进行分析。新乡市主城区包含红旗区、卫滨区、牧野区和凤泉区,因凤泉区面积较小且未建设换电柜,无换电柜运营数据进行比对,故不计入研究区域范围内。
3.1 外卖配送电动自行车换电需求预测结果
基于POI数据的外卖配送起止点确定方法,得出新乡市主城区外卖配送起点(O)为16 个,配送止点(D)为11个,如图1所示。
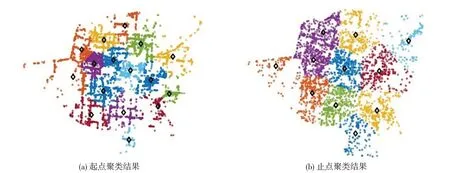
图1 外卖配送起止点聚类结果Fig.1 Clustering results of starting and ending points of take-out delivery
为利用仿真模拟新乡市主城区的外卖配送电动自行车换电需求时空分布,本文根据新乡市外卖配送相关情况,并结合相关研究成果设置换电需求仿真预测模型参数,如表1所示,其中,仿真时长设置为12 h,因为调研得到外卖配送时间大多处于8:00-20:00。

表1 换电需求仿真预测模型参数Table 1 Parameters of predicting model of battery swapping demand by simulating
基于上述参数设置即可模拟得到新乡市主城区外卖配送电动自行车一天内的换电需求时空分布预测结果。日换电需求的时间分布预测结果如图2所示,同时,图2也显示了根据某大型换电企业2022 年4 月—12 月的换电运营数据分析得出的日均换电需求分布。
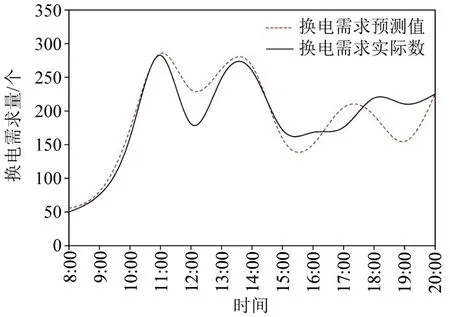
图2 换电需求时间分布Fig.2 Temporal distribution of battery swapping demands
由图2可知,日换电需求的时间分布预测值与日均换电需求的时间分布实际值变化趋势一致,且经计算,预测值与实际值的皮尔逊相关系数为0.83,表明两组数据具有极强的关联性,一定程度上验证了换电需求仿真结果的准确性。此外,图2表明,换电需求在11:00,14:00,17:00 和20:00 左右急剧增长,且11:00和14:00左右的换电需求量显著高于17:00 和20:00 左右的换电需求量,与文献[13]指出的外卖订单需求主要集中在午高峰(10:00-12:00)和晚高峰(16:00-18:00)两个时段,且午高峰时段的订单需求数量显著高于晚高峰时段的订单需求数量的结果一致。外卖配送电动自行车换电柜的服务能力如果满足需求高峰时段内的需求,即可以满足其他非高峰时段的需求,因此,在外卖配送电动自行车换电柜选址定容时,选取换电需求高峰时段11:00的需求数据。
仿真模拟得到的需求点位置如图3所示,各需求点的日换电需求量如表2所示。
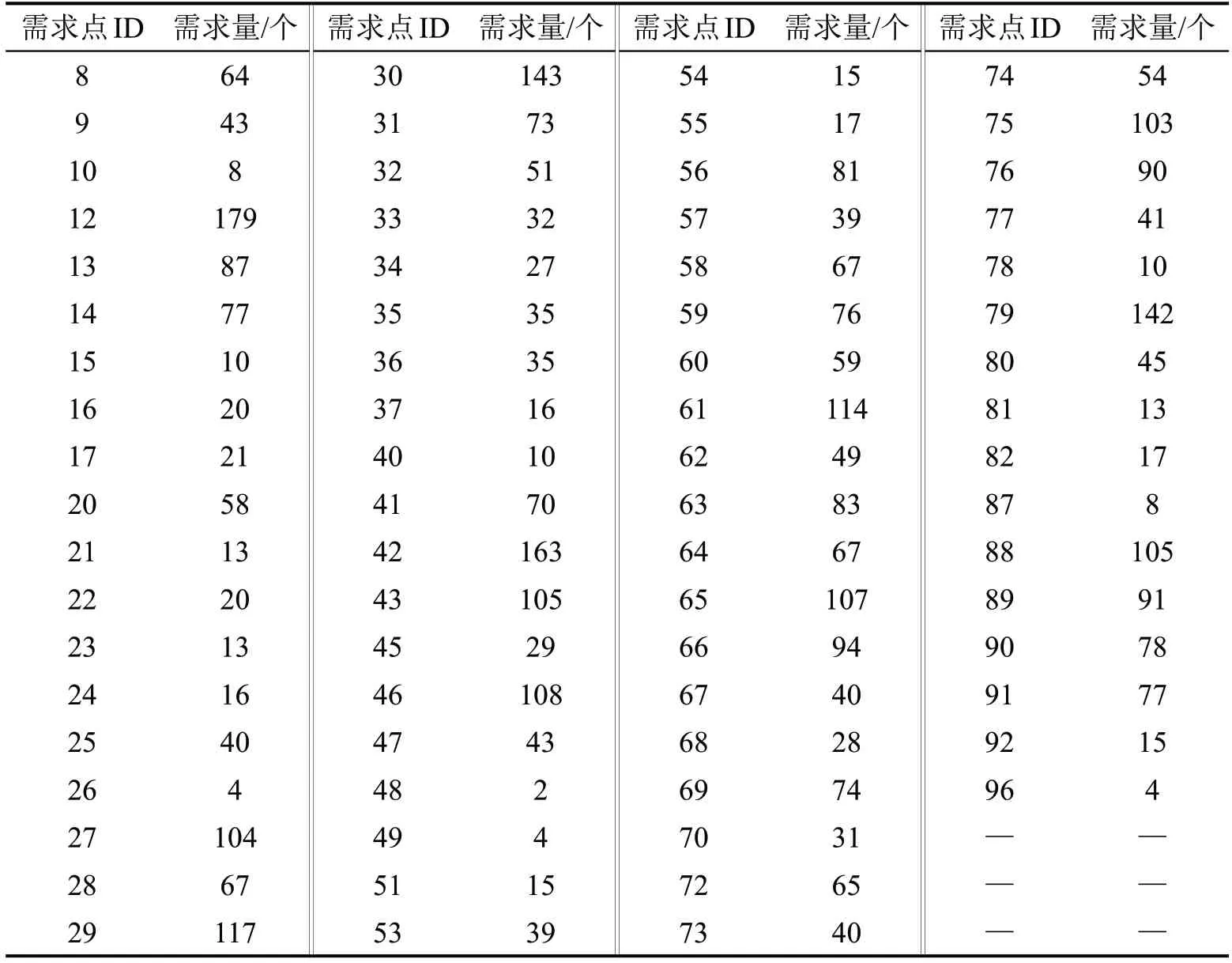
表2 各需求点日换电需求量Table 2 Daily demand for battery swapping at each demand point
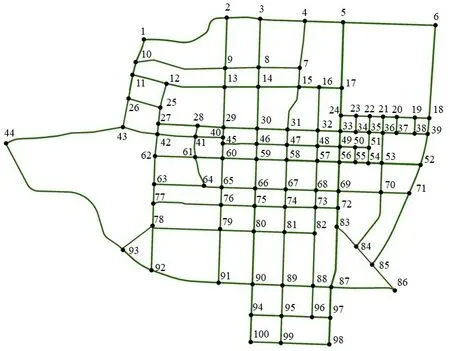
图3 换电需求点空间分布Fig.3 Spatial distribution of battery swapping demand points
3.2 外卖配送电动自行车换电柜选址定容结果
3.2.1 模型参数设置
根据外卖配送电动自行车换电柜选址定容模型可知,模型在进行求解之前需设定相关参数,为使求解结果更加接近现实,本文根据新乡市已建设的换电柜相关情况设定换电柜运营年限、电池使用年限、贴现率、换电柜的柜体成本、锂电池成本、换电柜中电池数量、换电柜的年电力成本和年设备维护成本;根据换电柜技术规范确定换电柜占地面积;根据网上公开数据推算新乡市主城区平均用地租金;通过对某大型换电企业调研设定需求惩罚系数;通过对外卖骑手调研设定用户对距离满意度变化的临界值的下限和上限。参数具体设定情况如表3所示。

表3 换电柜选址定容模型参数Table 3 Parameters of locating and sizing model of battery swapping cabinet
3.2.2 选址备选点确定
外卖配送电动自行车换电柜的选址不仅需要考虑用户的需求分布、换电行为特点及换电柜的服务半径等,还应符合城市规划要求,满足消防和疏散等安全要求,以及供电设施的供电约束等。综合考虑上述因素,筛选出新乡市主城区34 个换电柜选址备选点,分布情况如图4所示。
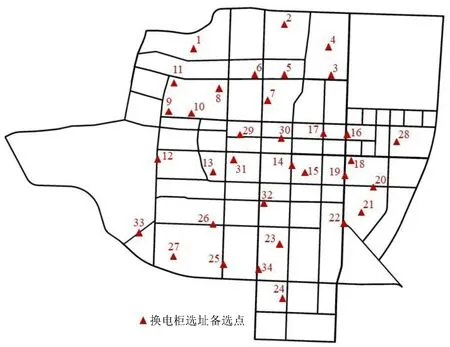
图4 换电柜选址备选点分布Fig.4 Distribution of alternative locations for battery swapping cabinets
3.2.3 模型求解结果
根据兼顾运营商和用户利益的外卖配送电动自行车换电柜选址定容模型特点,本文采用NSGA-II算法求解模型,初始参数设置如下:种群规模200,迭代次数500次,变异概率0.01,交叉概率0.8,求得45个最优的外卖配送电动自行车换电柜选址方案,如图5所示。为便于对比运营商总成本最低与用户满意度最高两个目标之间的关系,图5中将运营商总成本加上负号转化为收益。

图5 外卖配送电动自行车换电柜选址方案Fig.5 Locating scheme of take-out delivery electric bicycle battery swapping cabinets
由图5可知,同时兼顾运营商和用户利益的外卖配送电动自行车换电柜选址方案不能同时满足所有目标值均达到最优的要求,用户满意度的提高需以增加运营商总成本为代价,而运营商总成本的降低则会降低用户满意度。
3.2.4 方案评价与选择
为进一步评价选址方案,为运营商提供决策建议,本文分别对目标函数设置3种决策偏好权重方案,并对比不同权重组合下选址结果的变化,3种决策偏好设置下的换电柜规划方案优化目标值如表4所示。
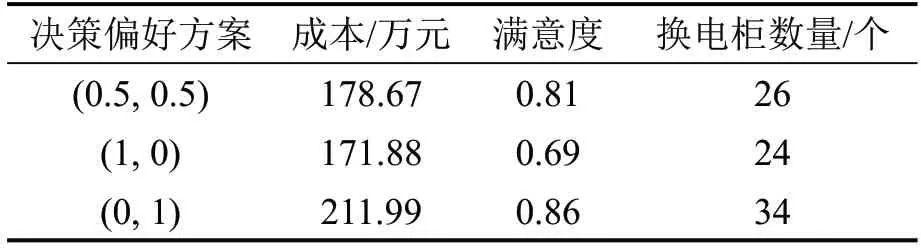
表4 3种决策偏好下的换电柜选址规划方案比较Table 4 Comparison of locating scheme of battery swapping cabinets under three decision preferences
由表4可知,与同时兼顾运营商利益和用户利益时的选址方案相比,仅考虑运营商利益的选址方案用户满意度降低了14.8%,运营商成本减少了3.8%;仅考虑用户利益的选址方案用户满意度提升了6.2%,运营商成本增加了18.6%。从运营商角度出发,既需要控制总成本,又需要增加用户粘性,因此,本文推荐同时兼顾运营商利益和用户利益的选址方案,运营商利益和用户利益同等重要时的换电柜选址定容方案如表5所示。
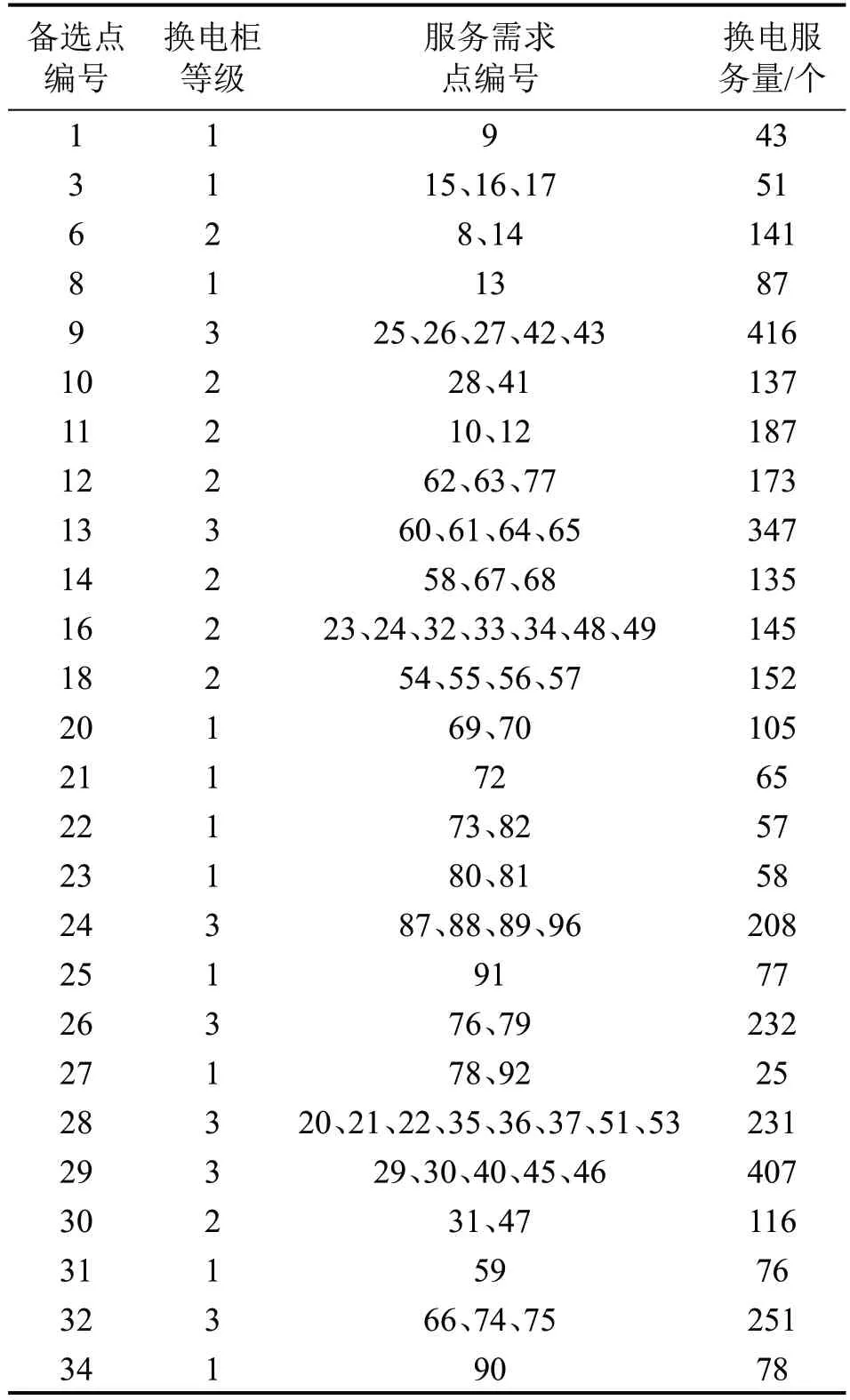
表5 运营商和用户利益同等重要时的换电柜选址定容结果Table 5 Locating and sizing results of battery swapping cabinets under scenario that interests of operators and users are equally important
3.2.5 换电柜建设数量对布局的影响分析
根据新乡市主城区已有换电柜的服务半径,新乡市主城区换电柜数量的下限为24,上限为34。为进一步验证本文提出的换电柜选址定容模型的有效性,本文以换电柜数量26 为起点,1 为步长分析换电柜建设数量对布局的影响,为换电柜建设时序提供参考。
换电柜数量从26 增加到30 的过程中,新增换电柜分别位于备选点15、7、19及17,如图6所示,且新增换电柜等级除备选点19处为2级以外,其余均为1级。继续增加换电柜建设数量时,新增换电柜位于备选点4,但此时该新增换电柜服务的换电需求量为0。综上所述,运营商可根据需要按照备选点15-7-19-17的顺序依次增加建设换电柜。
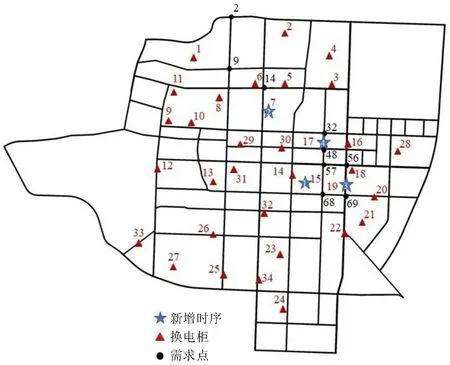
图6 换电柜建设分布Fig.6 Distribution of battery swapping cabinet construction
由图6 可知,新增的第1 个换电柜附近换电需求量较多,同时,新增换电柜前,需求点57 和68 由备选点18 和14 处的换电柜服务,距离相对来说较远,新增备选点为15 的换电柜位于需求点57 和68中间,缩短了用户换电距离,增加了用户满意度。此外,依次新增的其他3个换电柜均缩短了原来距离较远的换电服务,即新增备选点为7的换电柜缩短了需求点14 处的换电距离,新增备选点为19 的换电柜缩短了需求点56 和69 处的换电距离,新增备选点为17 的换电柜缩短了需求点32 和48 处的换电距离。
随着换电柜数量的增加,运营商利益和用户利益也随之发生变化,如图7所示。随着换电柜数量的增加,运营商总成本不断增加,用户满意度逐步上升,当建设30 个换电柜时,用户满意度最大,此后不再发生变化。因此,换电柜建设数量并非越多越好,否则,只会增加运营商总成本。
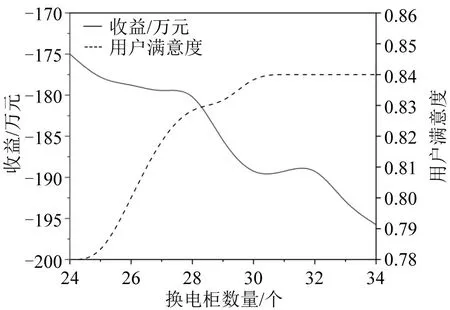
图7 运营商成本、用户满意度与换电柜数量关系Fig.7 Relationship of operator cost,user satisfaction and number of battery swapping cabinets
4 结论
本文得到的主要结论如下:
(1) 通过仿真模拟外卖配送电动自行车8:00-20:00 的出行行为,得到新乡市主城区外卖配送电动自行车换电需求在11:00,14:00,17:00和20:00左右急剧增长,且11:00和14:00左右的换电需求量显著高于17:00和20:00左右的换电需求量;模拟结果与换电柜实际运营数据在高峰时段及其订单量上基本吻合,验证了仿真模拟外卖骑手配送路径方法在换电需求预测上的合理性与准确性。
(2)换电柜选址方案不能同时满足运营商和用户利益均为最优,用户满意度的提高需以增加运营商总成本为代价;与同时兼顾运营商和用户利益时的选址方案相比,仅考虑运营商利益的选址方案使运营商成本减少了3.8%,但用户满意度降低了14.8%,仅考虑用户利益的选址方案使用户满意度提升了6.2%,但运营商成本增加了18.6%;同时兼顾运营商和用户利益时,新乡市主城区外卖配送电动自行车换电柜最佳建设数量为26,其中,容量为11的换电柜11个,容量为22的换电柜8个,容量为33的换电柜7个;新乡市主城区应按照备选点编号15-7-19-17 依次新增换电柜,当换电柜数量为30时,可使用户满意度最大,若继续增加换电柜建设数量,只会增加运营商总成本。

