基于交通波特征的车道级车流溯源方法
袁见,刘福强,安琨,郑喆,马万经*,俞秋田
(1.同济大学,道路与交通工程教育部重点实验室,上海 201804;2.麦吉尔大学,土木工程系,蒙特利尔H3A0C3,加拿大;3.浙江数智交院科技股份有限公司,杭州 310000)
0 引言
以往,常规信控路口的缓堵思路为对排队较长的相位增加时空资源,而对上游路口应如何调整则缺乏参考依据。车流溯源能为上下游路口管控方案的联合优化指引方向,是量化诊断拥堵成因,实现从“缓堵”向“治堵”突破的关键之一。要获取车辆的完整来源路径,需要在待溯源路段上游完整布设可识别车辆身份的摄像头等传感设备[1]。因此,如何利用覆盖范围更广的低渗透率轨迹数据进行信息挖掘就成了关键。
全样本轨迹重构是目前最接近于车流溯源的技术手段,其目的在于基于已有轨迹数据,估计其他无定位信息车辆的完整轨迹。现有快速路场景的全样本轨迹重构主要聚焦于主干线的车辆轨迹重构,很少涉及上下匝道车辆[2],因而难以进行溯源分析。在城市信控场景中,现有轨迹重构方法通常先基于抽样轨迹重构交通波几何特征,再假设所有车辆服从均匀分布[3],进而推算得到路口或干线的单车道直行车流全样本轨迹[4-5]。除单车道场景外,唐克双等[6]融合视频车牌和线圈流量数据,提出一种支持多车道场景换道的轨迹重构方法。针对上游存在固定检测器的场景,学者通过并引入跟驰、换道等多种约束条件,生成并筛选出最合理的轨迹运行状态[7]。然而,车流溯源还需要知道直行车辆在支线上的具体驶入路段与驶离路段。上述系列方法虽应用了多源数据,能基于检测器判断支线驶入车辆数量、基于车道功能判断车辆驶离情况,却不能支撑上下游驶入、驶离车辆的精准拼接,因而并未具备完整行驶路径的连续追踪能力。
交通波作为一种反映车辆密度变化的特征,已被广泛应用于排队长度、延误分析等交通运行状态分析中[8]。其中,集结波反映了车辆排队队尾位置随时间变化的曲线,是需求与交通时空资源供给相互作用后的结果,一定程度上反映了交通需求特征。然而,鲜有研究探讨过交通波用于溯源的可行性,以及基于交通波特征的具体溯源方法。现有研究表明,只需要20%及以上的浮动车渗透率,即可实现对交通波特征的高质量估计[9-10]。根据Sun等[11]的研究结果,在一个周期内即便只有一辆车有代表性轨迹,也能拥有较高的交通波估计精度。因此,只要验证交通波特征能够为车流溯源提供正向信息,则基于交通波特征的车流溯源方法就具备现实可行性。
对此,本文结合集结波几何特征和信号配时参数,探索集结波在车道级车流溯源方面的应用潜力,并基于真实场景数据集NGSIM 对提出的方法效果进行测试。
1 问题介绍与特征参数提取
1.1 车流溯源问题介绍
车流溯源包括网络层面、路段层面两种不同的分析尺度。目前,大部分溯源研究均为网络层面。这类研究通常以行程时间、流量等以路段为基本单位的信息为输入。然而,这类信息通常采集时间范围长且不按车道统计,因而网络层面溯源难以支撑单车道、单信号周期的溯源分析。对此,本文从微观层面提出一种面向城市道路上下游相邻路段的车流溯源场景:设待溯源路段包含M条车道,上游来源路段总数为N,总观测信号周期数为T,一条集结波包含特征参数数量为Q。则第m条车道在第t个信号周期的集结波特征集合为,车辆来源真实值集合为,其中,q和n分别为特征参数索引和上游来源路段索引。则车流溯源问题的目标在于基于特征参数fm,t,估计得到尽可能准确的ym,t。这一研究场景设定能对单车道、单周期内的车辆进行分析,局限性在于推算连续多路段溯源结果时,由于中间路段仅有部分车辆驶入待溯源路段,对某一部分车辆进行精确溯源,在这一框架下还较为困难。
现实应用中,可通过在上下游路段架设临时检测器以获取ym,t真实值,以便用于相关模型的训练以及结果验证。在评价指标方面,使用均方误差(Mean Square Error,MSE)和平均绝对值误差(Mean Absolute Error,MAE)作为模型评价指标。
1.2 交通波特征参数提取
交通波的提出借鉴了流体力学理论,当交通状态发生变化引起车队密度改变时,其分界面会在车流中传播,其在时空二维上会形成几何多边形。在车道层面,交通波可以理解为排队长度随时间变化的曲线。当车辆到达路口减速形成排队,就产生了集结波,这一过程就如同“石子”落入水中产生的“涟漪”。通过对涟漪形态的判断,能够反推出石子的大小。在这一灵感的促使下,本节探寻基于交通波获取车流来源的可能性。
为量化分析交通波特征,构建交通波的若干参数如表1 所示。集结波斜率集结波持续时长,覆盖最大排队长度。为便于理解,图1(a)列举了交通波图示场景;图1(b)为一个源自NGSIM(Next Generation Simulation)数据集的真实交通波案例。该案例设置tr=0,图中只显示每辆车轨迹在该信号周期内的第1 个停车点位的位置信息。集结波斜率采用线性回归拟合得到。可以看到,该集结波总计由7辆车组成,起始时空位置为(-0.40,1.67),结束时空位置为(15.10,43.06),斜率为2.654,交通波持续时长为15.5 s,覆盖最大排队长度为41.39 m。
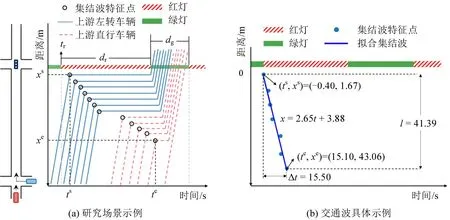
图1 研究场景及具体交通波参数示例Fig.1 Research scenario and specific example of traffic shockwave
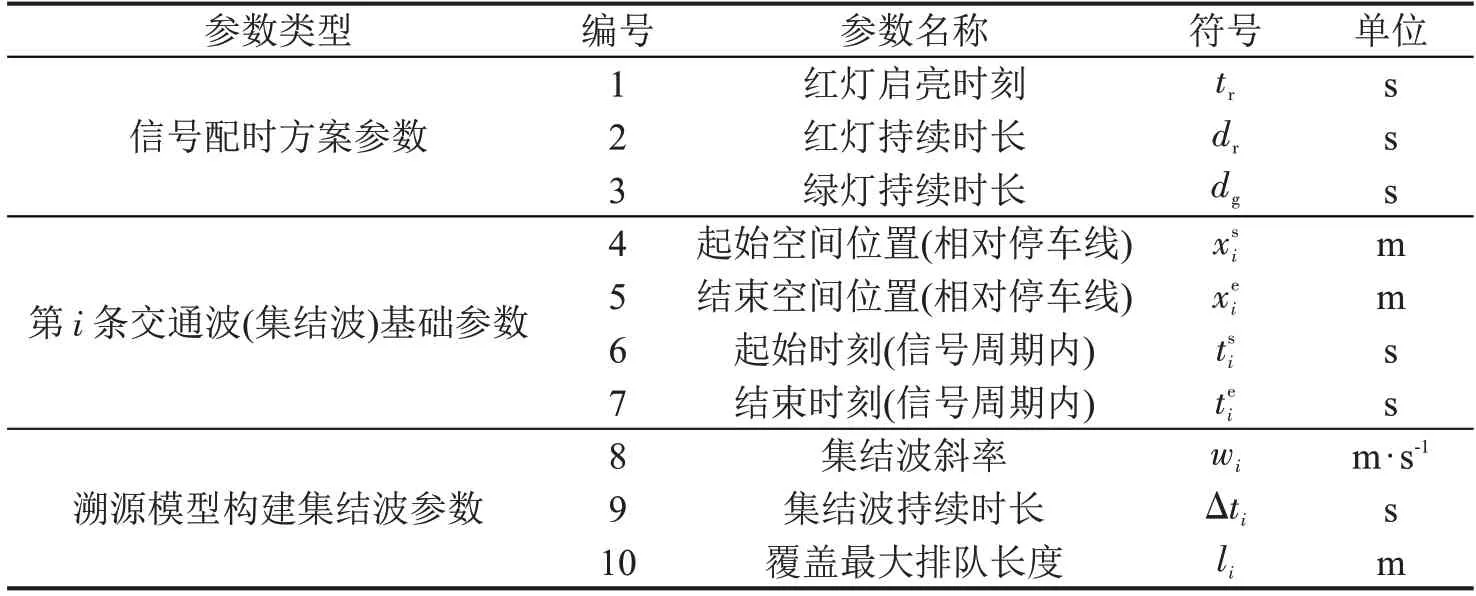
表1 基于交通波的车流溯源模型特征参数表Table 1 Parameters of shockwave-based traffic flow tracing model
2 交通波特征溯源可行性分析
为验证交通波应用于溯源分析的可行性,采用NGSIM 数据集进行统计分析。图2(a)为数据采集范围的俯视图,分析区域及上游路段已用阴影与文字进行标识。
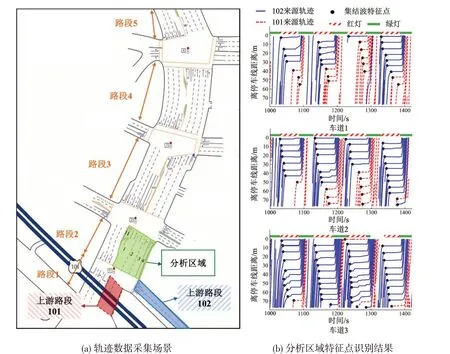
图2 NGSIM数据采集场景及交通波特征点识别结果Fig.2 NGSIM data scenarios and results of traffic shockwave feature identification
2.1 数据预处理
数据预处理包括车辆距离停车线距离计算、信号配时方案提取、集结波特征点识别与参数提取这3 个步骤。各条车道的轨迹数据单独处理,预处理部分结果如图2(b)所示。可以看到,所提出的识别逻辑能够准确地识别出轨迹中与集结波相关的特征点。最后,采用线性拟合即可得到集结波的斜率。
需要注意的是,可行性分析的目的是分析不同来源车辆的交通波特征差异,这里知道车辆的准确来源,可将交通波按照来源进行精确切分,因而单周期内可能存在多条交通波。在后续的模型输入中,由于现实中并不能知道交通波中不同来源车辆的分界点,因而在一个信号周期内,一条车道的输入信息只有一条交通波参数。
2.2 不同来源交通波统计分析
为分析不同来源车辆交通波的时空分布特征是否具有显著差异,将不同信号周期的集结波映射到一个信号周期内,并从一维(车辆初次停车时刻)和三维(集结波起始时空位置及覆盖长度)分别分析,使用数据为图2中分析区域车道1~车道3。
(1)信号周期内车辆初次停车时刻分布
对不同来源车辆在信号周期中的初次停车时刻进行统计,设红灯启亮时刻为0 时刻,统计结果如图3 所示。其中,101 与102 分别代表上游直行到达与上游右转到达车辆。可以看到,来自101车辆的停车时刻主要集中在30~60 s,而来自102的车辆则集中在0~40 s。这说明,不同来源车辆在初次停车时刻这一维度上已有明显的统计特征差异。
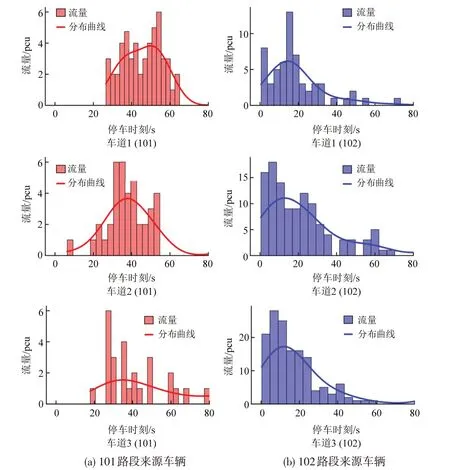
图3 信号周期内车辆首次停车时刻及分布特征曲线Fig.3 Distribution of vehicles'first stop time during traffic signal cycle
(2)集结波三维分布特征
为寻找不同来源车辆在交通波层面更为显著的统计特征差异,从集结波起点所处的时间位置、起点离停车线距离、覆盖最大排队长度这3个层面对其特征进行分析。采集到3 条车道在20 个信号周期内总计86条集结波,其特征参数可视化如图4所示,图中3 个二维散点图分别为3 项特征在二维平面上的两两组合。可以看到,3 项特征参数在二维层面上均有一定程度的相互分离特征。更进一步,将其在三维层面进行组合,可以看出较为明显的区分。这充分说明在这一场景下,不同来源车辆所形成的交通波特征确实具有差异性。综上,基于集结波特征进行溯源分析具有一定可行性。

图4 NGSIM交通波特征参数多投影面统计分析Fig.4 NGSIM multi-projection statistical analysis of traffic shockwave parameters
3 基于机器学习的溯源模型及结果分析
考虑到不同场景下交通波特征受多种因素影响,并且这些因素之间的关系可能呈非线性,因此使用机器学习的方法对该问题进行建模分析,以捕获输入特征之间的非线性关系。
3.1 数据归一化与数据输入模式
由于模型输入的各项特征量纲不一致,为提高模型训练效果,需对数据进行归一化处理。本文采用Min-Max 归一化和Z-Score 两种方法,以为例,计算方法为
结合问题特征,测试两种数据输入模式:模式1,只输入自身车道交通波特征;模式2,除输入自身车道交通波特征之外,还输入同路段同周期其他车道的交通波特征。两种输入模式如图5 左下方所示。以路段1 为例,模式1 输入的是路段1 本身的参数与标签,而模式2 则在模式1 的基础上额外增加路段2 和路段3 的交通波特征参数(输入特征数量为模式1的3倍)。第2种输入数据的形式主要考虑为:在流量相对稳定的情况下,不同车道流量分布会造成不同的交通波特征。因此,同一个路段不同车道的交通波特征是存在一定关联性的。进而,在对车道进行溯源分析时,其他车道的信息同时也能够为其提供一定的信息量,有可能提升溯源模型的准确程度,也有可能提升对训练所需数据量的需求。后续将对这两种输入模式的效果差异进行测试分析。
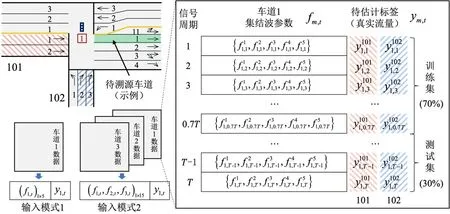
图5 溯源模型两种输入模式及数据格式示例Fig.5 Two input modes and data format example of flow tracing model
3.2 机器学习模型及训练方式
在机器学习模型中,分别构建线性回归(Linear Regression)、决策树回归(Decision-Tree Regression)、随机森林回归(Random Forest Regression)和梯度提升回归(Gradient Boosting Regression)这4 种代表性多输出回归模型进行测试。这4种模型之间有一定递进关系,复杂度逐渐增加,能够应对更复杂的数据关系。所有模型均基于开源程序库sklearn展开测试。同时,多输出回归模型可以处理具有多个目标变量的情况,每个目标变量都是一个独立的回归问题。因此,模型输出数量可与来源数量一致,可适用于具有不同拓扑结构场景。以车道1为例,整理后的参数及标签数据形式如图5右侧所示。其中,模式1 输入的变量为5个,模式2输入的变量为15个。为验证模型效果,整个数据集将按照7∶3 的比例划分为训练集和测试集。
由于现实中不同时段交通需求水平及分布特征不同,车道功能及信号配时方案也可能不同。因此,为降低模型训练难度,本文提出模型的定位为分时段训练模型,即应用于早高峰与晚高峰的模型并非使用同一数据,而是分别使用对应时段的数据训练。
3.3 案例分析
(1)实验设计
案例分析选择图2 中的待溯源路段。该路段总计有5条车道,包括1条直左车道,2条直行车道,1 条直右车道,1 条右转车道。由于直左车道流量过少(2000 s 内仅有25 辆车)以及右转车道不受信号灯控制,无法形成足够的交通波样本,因此,仅对编号2、3、4 这3 条车道进行溯源分析。3 个车道单信号周期内到达车辆数分布直方图如图6 所示。从统计结果来看,单车道在单周期内最多到达车辆数约为17 辆,平均值约为10 辆。这一数据将为后续模型效果提供参考依据。

图6 3个车道单信号周期内到达车辆数分布直方图Fig.6 Distribution histogram of number of arriving vehicles within a single cycle in 3 lanes
其次,在数据量方面,由于NGSIM原始数据采样时长有限(总计2000 s,20个信号周期),单车道仅有20 个样本数据,不足以支撑机器学习算法的模型训练需求。为探究得到有效模型具体所需要的数据量,需要在不同日期同时段内多次进行数据采样过程。对此,本文假设不同日期同时段内的数据具有相似特征,并引入高斯噪声对现有数据加入随机波动,以模拟现实中同时段内多次采样过程,扩样倍数分别为1倍、2倍、5倍、10倍。为克服模型随机性的影响,每个结果采用50 次测试结果的平均值。
(2)结果分析
基于上述实验设计方案,对基于Min-Max归一化和Z-Score归一化得到的结果分别列举进行对比分析,得到3 条车道的溯源误差平均值如表2 所示。对比两种归一化方式发现,采用Z-Score 归一化方法整体效果相对更优,特别是在数据量提升到5倍(100个信号周期)及以上时,随机森林回归与梯度提升回归效果有明显优势。使用线性回归方法时,使用两种归一化方式无明显区别。横向对比两种数据输入模式:在数据量较少的情况下,发现输入模式1 的发挥更优,而输入模式2 的误差则非常高,尤其是线性回归;当数据量提升时,输入模式2的优势逐渐体现;当数据量提升到5 倍及以上时,输入模式2 效果反超并优于输入模式1。这说明,输入模式2由于输入变量数量提升,因此对数据量的要求相对更高,同时模型的潜力也更大。特别是在Z-Score 归一化方法下,当数据量达到10 倍时,梯度提升回归模型的MAE 能够低至0.01,仅占平均流量的0.10%,且误差最大不超过5.90%。这一实验结果也能为现实溯源应用提供指导,当采集数据量有限时(采集时长低于4000 s,或覆盖周期数量少于40 个),宜采用输入模式1。即便只有20 个信号周期的初始数据,输入模式1所取得的最差结果中,MAE为2.36,约占图6显示平均流量的23.60%,而同场景下的输入模式2,最大误差可达到50.80%。
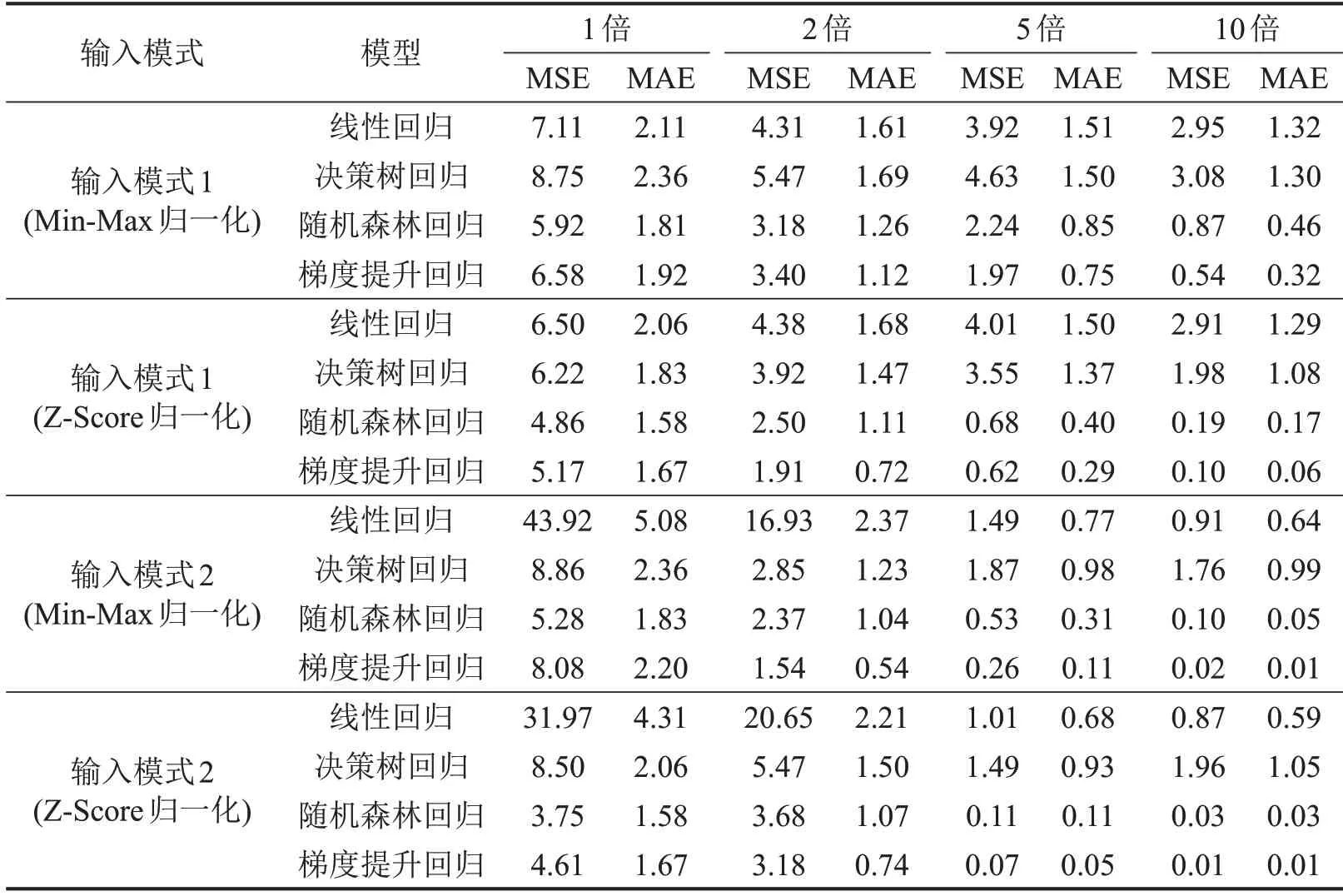
表2 基于NGSIM数据集的溯源模型效果Table 2 Performance of flow tracing model based on NGSIM dataset
最后,为分析各模型在不同数据精度下的适应性,给初始数据定位附加不同上限的正态分布误差,进行灵敏性分析,得到结果如图7所示。其中,数据采用Min-Max归一化方法处理,初始数据扩样系数为10 倍。由于测试场景路段为80 m,50 m 的误差上限已能够覆盖全路段,因此设置50 m 为实验分析上限。可以看到,随着数据误差上限的提升,模型的误差也在提升。以图7(a)MSE 为例,对比5 m与50 m定位精度,线性回归、决策树回归、随机森林回归、梯度提升回归的误差提升比例分别为36.4%、34.4%、143.3%、93.6%。最后两种方式虽然误差上升明显,但仍比前两种方式要好。可以看到,不同模型对误差的适应能力有所差异。所有模型在数据误差较大时,整体并未出现失效现象。其原因可能在于,模型在训练时也将误差作为特征之一进行学习。在实际应用中,应结合数据量、数据质量进行综合考虑,进而选择最为合适的方法。
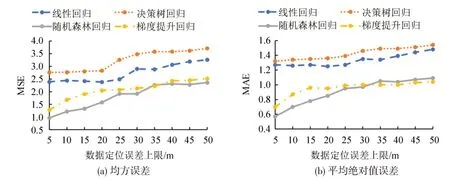
图7 不同定位误差场景下模型灵敏性分析Fig.7 Sensitivity analysis under different levels of data errors
4 结论
基于NGSIM数据集对不同来源的车流交通波统计分析发现,交通波中蕴含着车辆来源信息。对此,本文尝试引入交通波特征信息,结合信号配时参数,提出一种车道级车流溯源方法。基于真实数据集测试发现,通过交通波特征进行溯源分析具有可行性,所构建模型在不同的数据量、特征参数归一化处理方法下效果各有不同。结合本文研究结果,在现实应用中应根据实际的数据情况,包括数据量、源数据精度等,灵活采用合适的数据处理方式与特定的机器学习模型。基于车道的溯源结果,可为上下游路口管控方案的联合优化指引方向。未来可以进一步研究具备多场景通用性、可迁移性、适用于连续多路段的车流溯源模型,并探索不同来源数量下的模型效果。

