星型-三角形负泊松比结构的面内压缩刚度可调控特性
魏路路, 许世维, 朱国华, 赵 轩
(1. 西安建筑科技大学 机电工程学院,西安 710055;2. 长安大学 汽车运输安全保障技术交通行业重点实验室,西安 710064)
近年来,随着交通安全、能源危机及环境污染等问题愈发严峻,对汽车的车身碰撞安全及轻量化提出了更高的要求,迫切需求强度高且抗冲击性能优异的轻量化材料及结构。负泊松比结构因其独特的变形模式,优异的抗压痕能力[1]、剪切模量[2]、能量吸收性能[3]、阻尼特性[4]及可调控性等特点,使其在车身吸能构件[5]、车辆安全座椅[6]及汽车悬架[7]等方面均具有较好的应用前景。其中,负泊松比结构的可调控性是实现负泊松比结构在不同领域及构件中应用的关键。开展负泊松比结构面内压溃行为的可调控性研究可满足不同的功能目标需求,进一步推动其工程实际应用。
负泊松比结构的力学性能主要取决于微观几何构型,通过对微观几何构型的调控可实现不同的功能需求。因此,国内外学者对负泊松比结构的面内压缩性能开展了系统的研究。Theocaris等[8]利用均质理论方法研究了基体材料和孔壁角度对星型负泊松比结构泊松比的影响。Quan等[9]利用连续纤维3D打印工艺制备了内凹六边形结构,并研究了不同载荷方向下的面内力学性能,其压缩刚度及能量吸收能力分别提升了86.3%和100%。Dong等[10]利用3D打印技术制备了不同壁厚的AlSi10Mg基内凹六边形结构,采用试验方法揭示了不同胞壁厚度的内凹六边形结构的变形模式。Lu等[11]基于二维交叉手性结构得到了三维交叉手性结构,基于Timoshenko梁理论建立了该结构的解析解,预测X、Y、Z3个方向上的弹性模量和泊松比。为进一步提高负泊松比结构的力学性能,部分学者通过改变几何构型或引入新的结构组合得到了具有增强冲击强度的新型负泊松比结构[12-13]。Liu等[14]基于内凹六边形结构设计了一种空竹形负泊松比结构,并在结构中增加了横向和纵向肋板,其抗冲击性能及能量吸收性能与内凹六边形结构相比显著提高。Lu等[15]在星型负泊松比结构中嵌入圆形结构得到星型-圆形结构,其弹性模量及能量吸收性能均显著提升,并解决了负泊松比结构刚度不足的问题。卢子兴等[16]基于星型结构与双箭头结构得到了一种星型-箭头负泊松比结构。结果表明,在不同冲击速度下该结构均呈现出比星型结构更优越的能量吸收能力。马芳武等[17-18]基于双箭头结构设计了内凹三角形负泊松比结构,利用数值模拟的方法研究了内凹角对该结构面内力学性能的影响。
负泊松比结构复杂的几何构型使其在变形时往往呈现多个变形过程,这也使得不同变形阶段的力学性能明显不同,因此引起了较多学者对其力学性能的可调控性展开了研究。Hur等[19]通过对负泊松比结构胞元几何参数的调整,实现了对负泊松比管状结构的抗弯及抗扭刚度的可控性调整。Cheng等[20]采用变刚度因子(variable stiffness factors, VSF)方法设计了内凹拉胀超材料,从调节密实应变的角度实现其刚度的可调控性。Zhang等[21]利用相同方法设计了具有刚度可调的旋转孔板负泊松比结构。McCrary等[22]设计了一种可调节刚度和能量耗散的双向力学超材料,利用多目标遗传算法使其体积能量耗散最大化并确保单元不发生塑性变形。Zhang等[23]设计了一种刚度可调的组合式管状结构,通过合理地选择中心连接柱的长度使得管状结构的刚度可调且稳定性及抗压能力也显著提高。孙龙等[24]设计了一种新型刚度可调控负泊松比管状结构,发现圆管的刚度可通过密实点比例因子进行调控。然而,上述研究主要是通过诱导原始结构变为新结构的方式实现对其力学性能的调控,而未分析不同类型胞壁对负泊松比结构力学性能的作用机制,忽略了不同类型胞壁对结构力学性能的调控作用,无法从结构自身诱导变形及胞壁自身承载调控2个相结合的角度实现对负泊松比结构力学性能的最优调控。
本文以星型-三角形负泊松比结构为研究对象,利用面内压缩试验揭示其变形机制及不同类型胞壁对结构力学性能的作用机理,并分析面内压缩刚度的可调控性。设计非均匀厚度分布的STH结构,采用数值模拟方法研究其面内压缩初始刚度及强化刚度的自调节特性。讨论不同类型胞壁厚度比及胞壁角对STH的初始刚度及强化刚度可调控性的影响,确定初始刚度及强化刚度的临界点。通过对星型-三角形负泊松比结构面内压缩初始刚度及强化刚度的研究,揭示其面内压缩刚度的可调控特性,从而为新型负泊松比结构的设计奠定基础。
1 结构设计及有限元建模
1.1 星型-三角形负泊松比结构设计与制备
星型-三角形负泊松比结构(star-triangular honeycomb,STH)是由Wei等[25-26]设计的一种具有增强冲击强度的新型负泊松比结构,且该结构在面内压缩载荷下刚度可调控。STH的几何构型如图1所示,其微观几何结构主要包括以下几种参数,其中l为倾斜胞壁的长度,θ为胞壁与垂直方向的夹角,α为胞壁角。此外,STH的胞壁结构可分为不同类型,其中垂直胞壁W1,其壁厚为t1;三角形胞壁W2,其壁厚为t2;内凹胞壁W3,其壁厚为t3。

图1 STH的结构及几何参数
利用增材制造技术制备两种相对密度相同而胞壁角(α=30°,45°)不同的STH,试样的基体材料为不锈钢(316L)。为了避免面内压缩时尺寸效应的影响,试样由5×6个胞元组成,如图2所示。此外,考虑到面内压缩时STH在面外方向屈曲的影响,面外方向上的厚度B取15 mm。两种不同胞壁角的STH的详细几何参数如表1所示。

表1 不同胞壁角STH的几何参数

图2 STH试样
1.2 材料属性
基体材料的材料属性是模型准确性的关键因素。采用与STH相同的制备工艺得到3个标准拉伸试样,并在CMT5205万能试验机上以1 mm/min的恒定速度对试样进行轴向拉伸。利用引伸计对试样的应变进行测量,载荷数据由试验机的数据采集系统自动获取。通过对试样的拉伸测试得到316L的工程应力-应变曲线,然后再转化为真实应力-应变曲线如图3所示,由重复试验得到最终的力学性能参数如表2所示。

表2 316L材料的力学性能
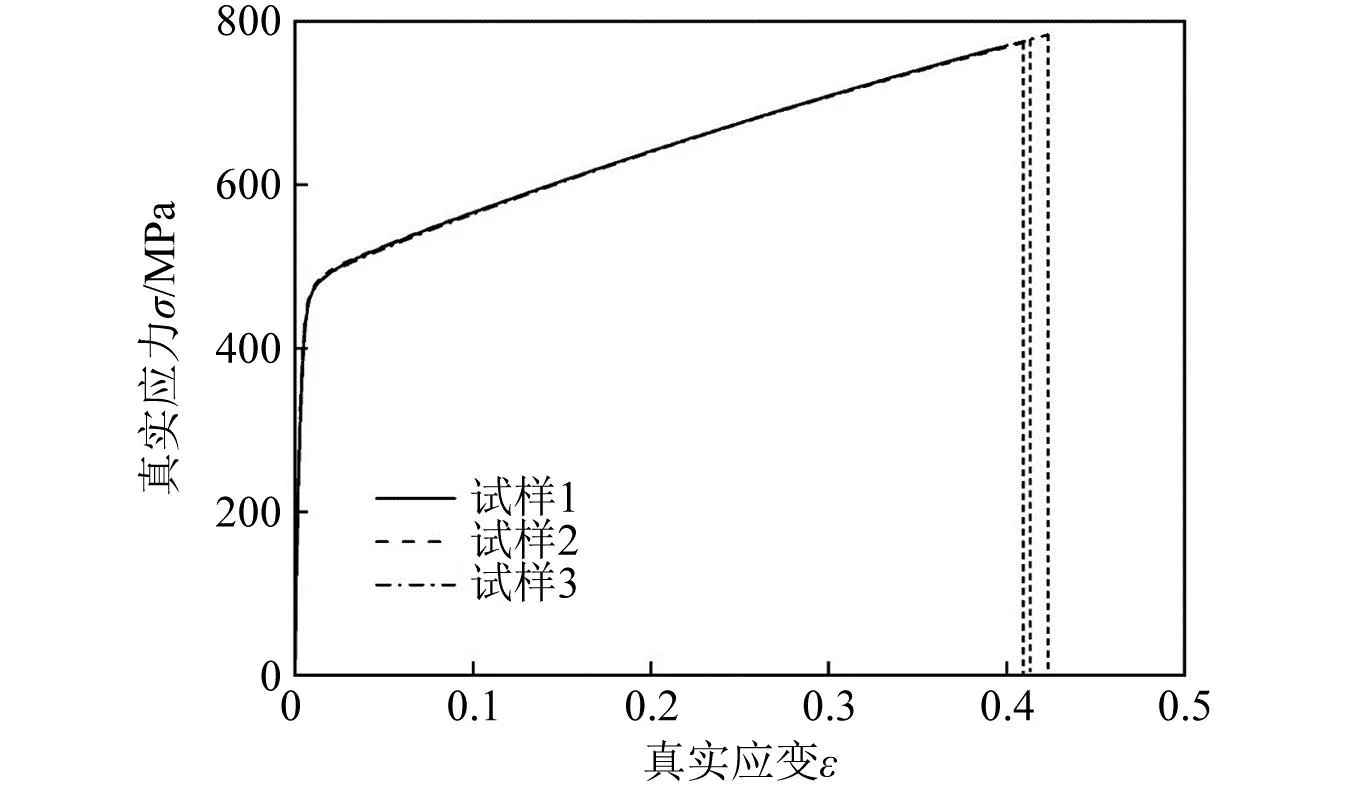
图3 基体材料316L的应力-应变曲线
1.3 有限元模型
利用非线性显式有限元软件LS-DYNA建立STH的面内压缩有限元模型,如图4所示。STH模型放置于上下刚性平板之间,约束下平板各方向上的自由度,上压板沿轴向方向以恒定的速度进行面内压缩。采用MAT#24材料模型模拟基体材料,其中基体材料的材料属性已在1.2节中测得,且数值模拟中不考虑基体材料的失效[27]。利用Belytschko-Tsay四节点壳单元模型定义胞壁,并沿单元厚度方向上定义5个积分点以保证模型收敛。通过网格收敛性测试分析确定网格尺寸,最终选择网格尺寸为0.5 mm×0.5 mm以平衡计算效率和精度,如图5所示。此外,为提高计算效率,z方向上的厚度设置为5个单元厚度,并约束模型在z方向上的自由度以防止模型在z方向上屈曲。采用“automatic single-surface”接触算法定义STH胞壁的接触以避免压缩过程中模型的相互穿透,利用“automatic surface-to-surface”接触算法定义STH与上下平板之间的接触,其摩擦因数取0.2[28]。在该模型中,上下平板采用5 mm×5 mm的壳单元模型,材料模型为刚性材料,其弹性模量、密度和泊松比分别为210 GPa、7 800 kg/m3、0.3。
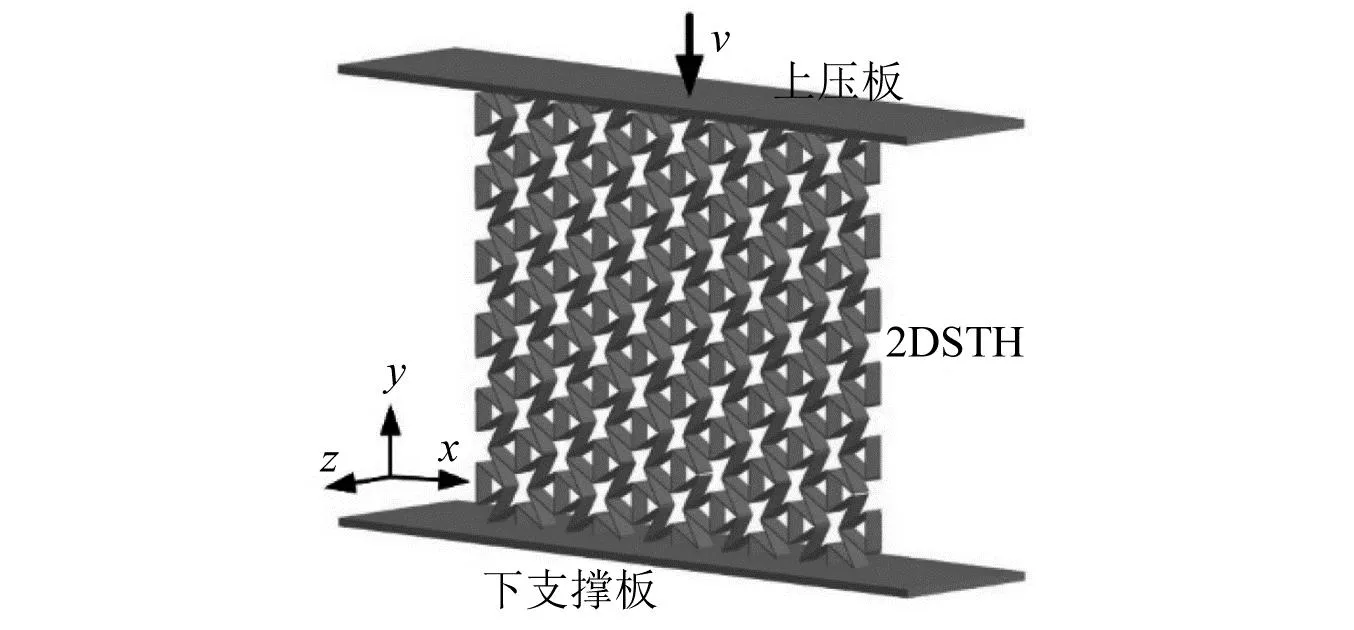
图4 STH的准静态面内压缩有限元模型

图5 网格尺寸收敛性分析
2 试验结果及模型验证
2.1 试验结果分析
对增材制造技术得到的STH试样进行准静态面内压缩,其试验在万能试验机(CMT5205)上进行。室温条件下,试样放置于下支撑盘上,上压盘以恒定的加载速度2 mm/min对试样进行轴向压缩,直至试样完全密实化。在试验过程中,试验机自动记录载荷及位移数据,试样的变形过程由数码相机以恒定的时间间隔记录。
准静态面内压缩载荷下STH的变形过程如图6所示。不同胞壁角的STH的变形模式相差不大,均呈现2个典型的变形阶段:内凹胞壁旋转收缩变为三角形格栅结构和三角形格栅结构的塑性坍塌。初始时刻(ε=0.05),靠近支撑端的胞元首先横向收缩变形并驱动STH整体横向收缩。但是,在变形过程中三角形结构无明显的变形,仅随内凹胞壁的收缩发生旋转变形,STH呈现出“X”形的变形模式。因此,STH的胞元随着压缩应变的增大逐渐横向收缩并向芯部聚集,呈现典型的负泊松比效应。受上下平板摩擦效应的影响,靠近平板的胞元横向收缩变形比芯部的胞元更弱,使得STH呈现出“<>”形变形模式,但是最终STH变形成非均匀壁厚的三角形格栅结构。其中,倾斜胞壁的等效厚度te是原始胞壁厚度t的三倍,而垂直胞壁的壁厚仍为t。随着轴向压缩载荷的增大,三角形格栅结构的胞元均匀地由固定端向压缩端逐层坍塌变形。由整个变形过程可以发现,内凹胞壁的旋转收缩诱导STH横向收缩并呈现负泊松比变形效应,然后使其变为新的三角形格栅结构以达到其功能的可调控目的。
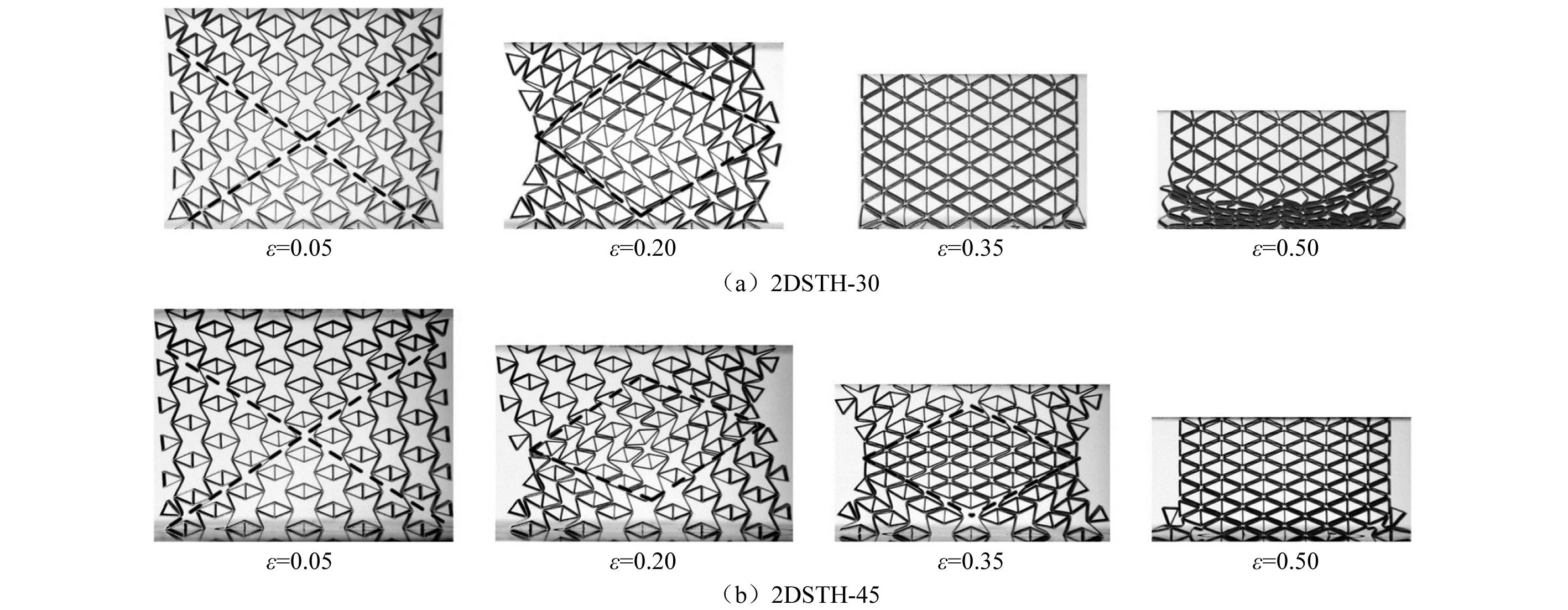
图6 不同胞壁角的STH的面内压缩变形模式
STH的局部变形过程如图7所示。可以明显地发现,第一变形阶段仅胞壁W3发生塑性屈曲,其他胞壁仅随胞壁W3的收缩变形发生水平运动,胞壁W3在该阶段主要承受压缩载荷;第二变形阶段,胞壁W2和胞壁W3堆叠在一起使得三角形格栅结构的倾斜胞壁等效壁厚增大,增强结构的承载能力,胞壁W1、胞壁W2和胞壁W3同时发生塑性坍塌;其中,胞壁W1为垂直胞壁,其轴向承载能力优异,压缩刚度和能量吸收性能均比其他胞壁更为优异。由此可得,STH的三种不同类型胞壁在不同变形阶段的承载机制,进一步地可以通过控制不同类型胞壁在不同变形阶段的承载性能实现对结构力学性能的调控。

图7 STH的局部变形过程
不同胞壁角的STH在面内压缩载荷下的应力-应变响应如图8所示。胞壁发生塑性屈曲前,应力-应变曲线呈现出第1个线弹性阶段,但其弹性模量E1较小。随着内凹胞壁的塑性屈曲,其应力-应变曲线呈现出第1个平台阶段σ1。当STH变为三角形格栅结构后,倾斜胞壁(三角形胞壁)的等效壁厚增大且垂直胞壁开始承受载荷,其应力-应变曲线呈现出第2个线弹性阶段,且弹性模量E2与E1相比显著增大。随着胞壁的塑性坍塌,应力-应变曲线呈现出第2个平台阶段,其平台应力σ2明显比σ1更高。
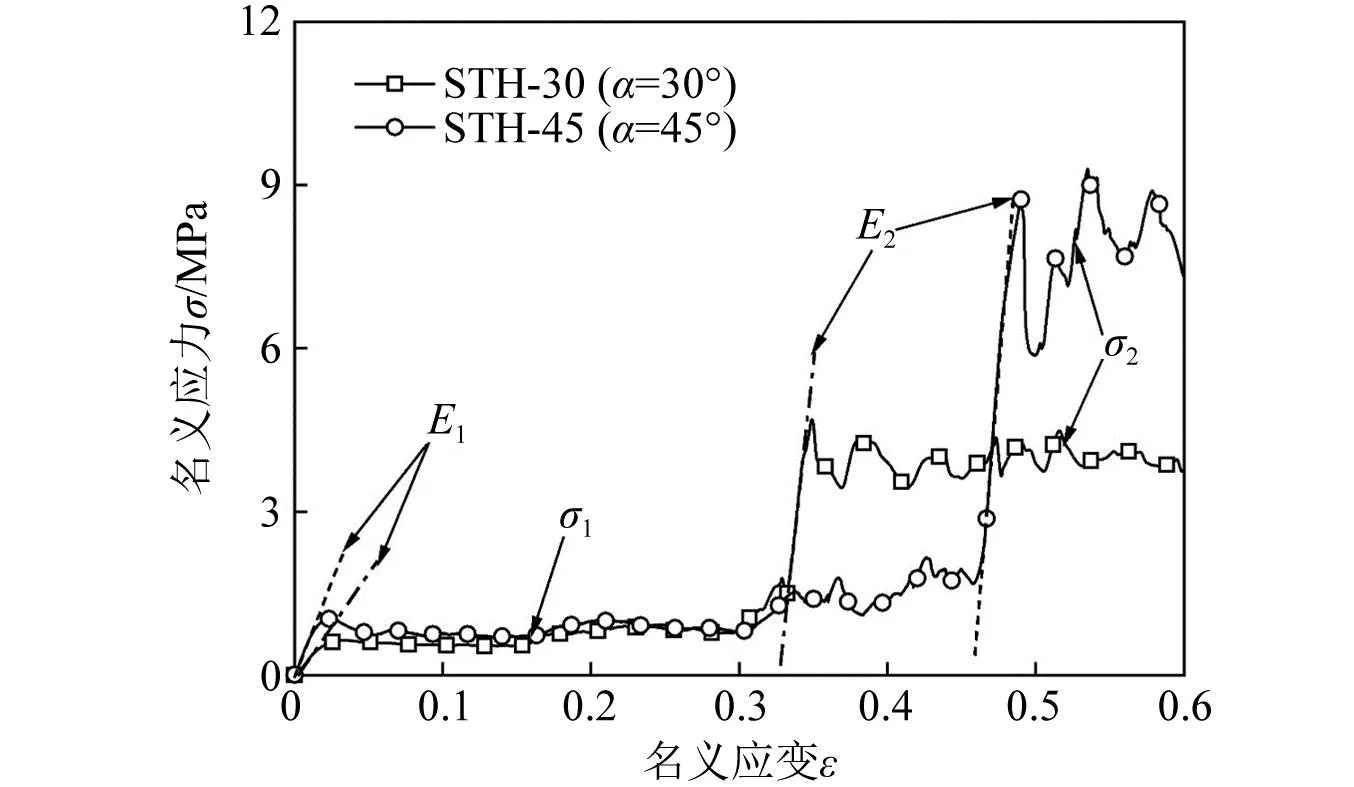
图8 不同胞壁角的STH的应力-应变曲线
由此可以发现,STH在面内压缩载荷下的压缩刚度及强度均可随着压缩应变的增大实现自我的调控,刚度及强度均逐渐增强,从而提高了结构的承载能力。但是,这种由结构自身变形实现的力学性能自调控特性仅能增大第二变形阶段的力学性能,STH在第一变形阶段的力学性能仍无明显改善。然而,基于不同类型胞壁在不同变形阶段的变形顺序及承载机制,控制其在不同变形阶段的承载能力,可进一步的改变STH在不同变形阶段的力学性能。
2.2 模型验证
为了验证建立的有限元模型的准确性,将胞壁角不同的STH的数值模拟结果与试验结果进行对比,如图9所示。
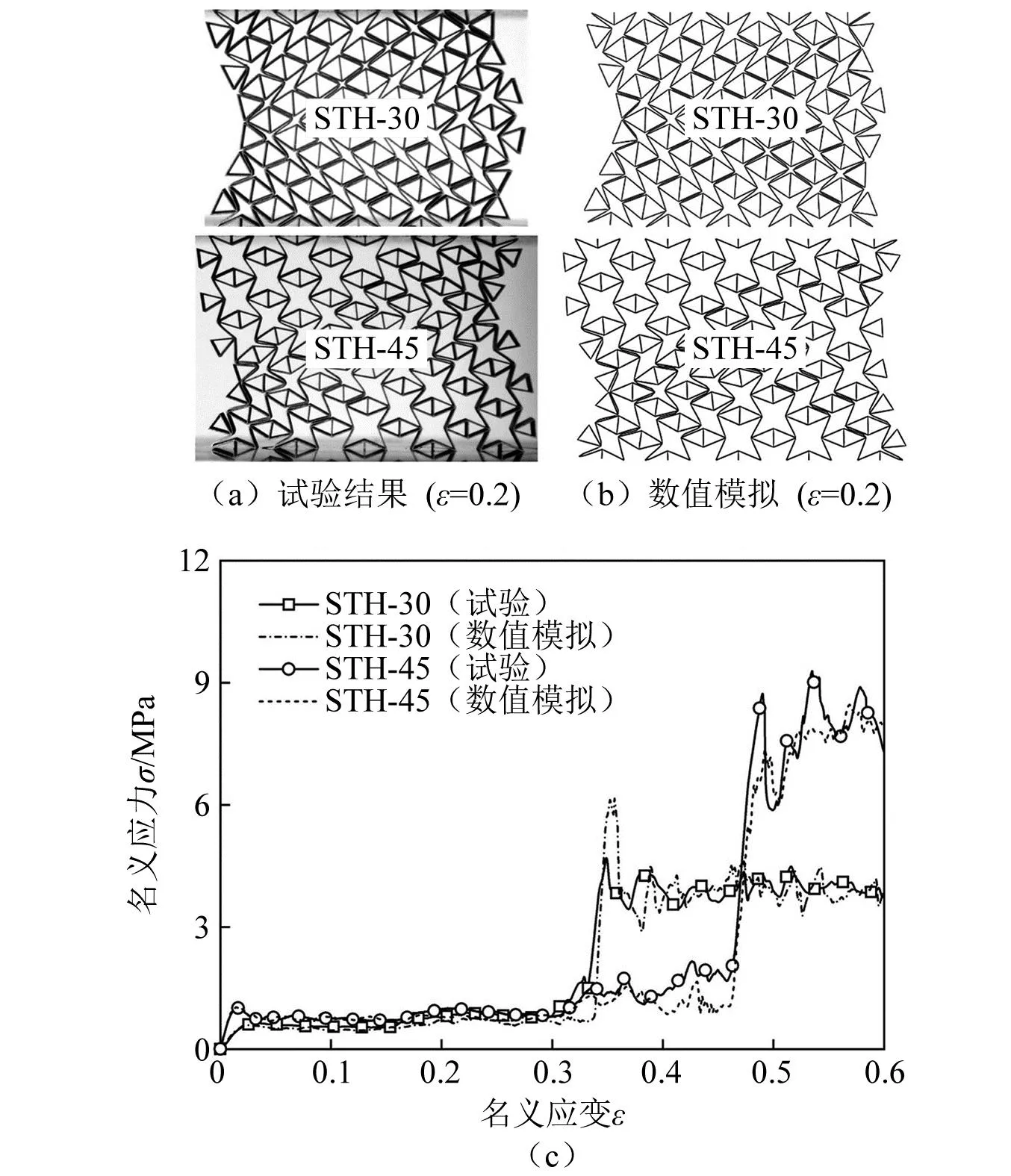
图9 STH的面内压缩试验与数值模拟对比
虽然在压缩过程中数值模拟结果的胞元变形与试验结果仍存在微小的误差,但是整体的变形模式具有较高的一致性。试验和数值模拟得到的应力-应变曲线变化趋势具有较高的一致性,但在应力增强阶段和密实化阶段两者存在一定的误差。这是由于试样制造过程中的误差、建模中的理想化处理及胞元密实化阶段的非均匀变形等原因导致的。但是,在整个变形过程中,试验与数值模拟得到的应力-应变曲线之间的误差并不大,可以被接受。因此,综合试验和数值模拟得到的应力-应变曲线及变形模式的对比可得,本文建立的STH的面内压缩有限元模型具有较高的精度,可以用于后续的数值模拟研究。
3 数值结果与讨论
由STH在面内压缩载荷下的变形承载分析可得,内凹胞壁W3主要在第一变形阶段旋转屈曲,且主要控制初始刚度和第一平台阶段的应力值。胞壁W1和W2主要在第二变形阶段发生坍塌,控制强化刚度及第二平台阶段的应力值。因此,通过对不同变形阶段胞壁承载能力的控制可达到对其刚度的调控目的。
3.1 不同类型胞壁STH的刚度可调控性
基于胞壁承载能力的不同,分别将垂直胞壁、三角形胞壁和内凹胞壁进行归类,以此设计三种质量m相同而胞壁厚度分布不同的STH如图10所示。三种结构的详细几何参数如表3所示,其中:STH-30-1的胞壁厚度均相同;STH-30-2的垂直胞壁和内凹胞壁厚度相同且大于三角形胞壁的厚度;STH-30-3的垂直胞壁与三角形胞壁厚度相同但小于内凹胞壁的厚度。
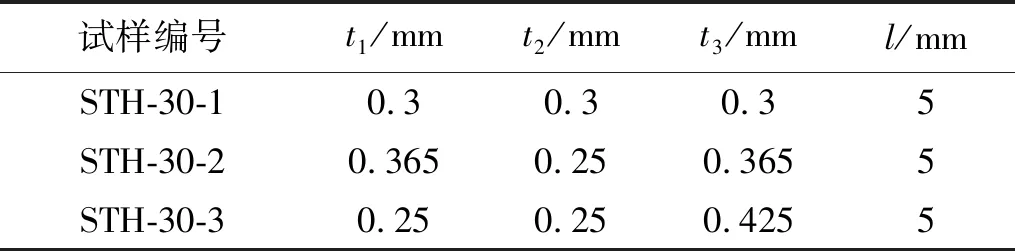
表3 三种不同壁厚分布的STH的几何参数

图10 三种不同壁厚分布的STH
准静态面内压缩载荷下非均匀壁厚的STH的面内压缩变形如图11所示。非均匀壁厚的STH在变形过程仍为胞元横向收缩变为三角形格栅结构,然后胞元逐层坍塌的变形模式。但是,在STH横向收缩变为三角形格栅结构过程中,其变形模式存在较大的差异。均匀壁厚的STH-30-1在面内压缩载荷下为全局横向收缩变形,呈现出典型的“X”型和“<>”型变形模式,如图11(a)所示。STH-30-2在面内压缩载荷下也呈现出典型的“X”型和“<>”型变形模式,但是三角形胞壁的厚度较小导致胞元的横向收缩不均匀,使其呈现出整体向右弯曲膨胀的变形模式,如图11(b)所示。STH-30-3的变形模式与其他两种结构相比明显不同。在压缩初始时刻,STH-30-3的胞元已开始向右侧膨胀变形,呈现出“>”型变形模式。随着压缩应变的增大,STH-30-3的“>”型变形模式进一步扩展,呈现出明显的左侧横向收缩,而右侧向外膨胀的变形模式,如图11(c)所示。然而,受芯部胞元横向收缩的拉伸作用影响,右侧向外膨胀的胞元最终也向芯部聚集,STH-30-3也变为三角形格栅结构。由于垂直胞壁和三角形胞壁的厚度均明显小于内凹胞壁的壁厚,三角形结构的承载能力明显不足,使得三角形胞壁在面内压缩载荷下首先发生塑性屈曲,等效壁厚增强的倾斜胞壁并未发挥有效的承载能力,如图11(c)所示。最终,三种结构变为三角形格栅结构后其局部首先发生塑性屈曲,然后向整个结构扩展。
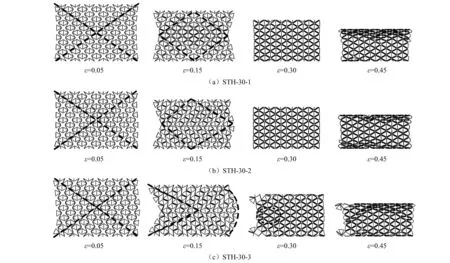
图11 不同壁厚分布的STH的变形过程
面内压缩载荷下三种不同结构的应力-应变响应如图12所示,其变化呈现出明显的差异。均匀壁厚的STH-30-1呈现出2个明显的线弹性阶段,且强化刚度Ec明显比初始刚度Ef更大。STH-30-2在面内压缩时也呈现出2个线弹性阶段。胞壁W1和胞壁W3的厚度增大时,等效壁厚2t2+t3=0.865<3t=0.9 mm虽然减小,但胞壁W3的承载能力显著提升,使得STH-30-2在第一变形阶段及第二变形阶段的承载能力均显著增强。总质量不变条件下,初始刚度Ef2和强化刚度Ec2分别比Ef1和Ec1增强了63.82%和37.89%,实现了通过改变不同类型胞壁厚度控制结构刚度的目的。STH-30-3的应力-应变曲线仅具有初始刚度Ef3,然后应力值逐渐增大,未呈现出明显的强化刚度阶段。这是由于胞壁W2和胞壁W3的厚度均显著减小,其承载能力明显不足,内凹胞壁发生塑性屈曲时也诱导其发生了一定的塑性屈曲,使得应力值呈现梯度增大的变化过程。
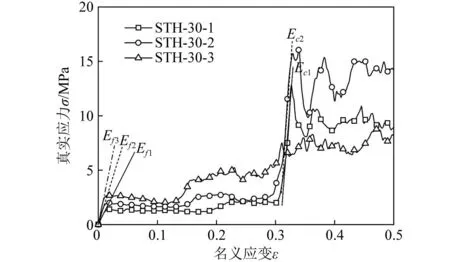
图12 不同壁厚分布的STH的应力-应变响应
由不同胞壁厚度分布的STH的应力-应变曲线变化可得,基于不同类型胞壁在不同变形阶段的承载特性,调节其壁厚可实现结构初始刚度和强化刚度的可调控目的。增大内凹胞壁及垂直胞壁的厚度可同时增强初始刚度及强化刚度,改善结构的力学性能。然而,增大内凹胞壁厚度只提高初始刚度,应力值呈现出逐渐递增变化趋势,且强化刚度阶段消失。
3.2 不同类型胞壁厚度比对刚度可调控影响
基于3.1节中的分析,取内凹胞壁与垂直胞壁的厚度相同(t1=t3),分析(t1=t3)/t2对STH初始刚度及强化刚度的影响。不同(t1=t3)/t2的STH的面内压缩应力-应变响应如图13所示。
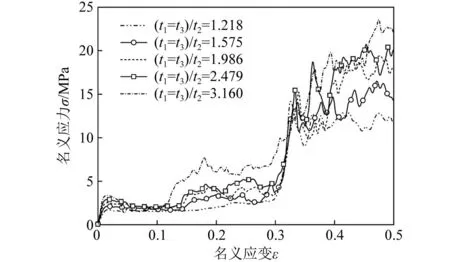
图13 不同(t1=t3)/t2的STH的面内压缩应力-应变响应
随着(t1=t3)/t2的增大,STH的应力-应变曲线由2个线弹性阶段(初始刚度和强化刚度)逐渐变为只有第1个线弹性阶段。这是由于三角形胞壁的壁厚减小后承载能力不足,STH变为三角形格栅结构过程中过早的发生了塑性屈曲导致的,与3.1节中的分析相同,如图14所示。
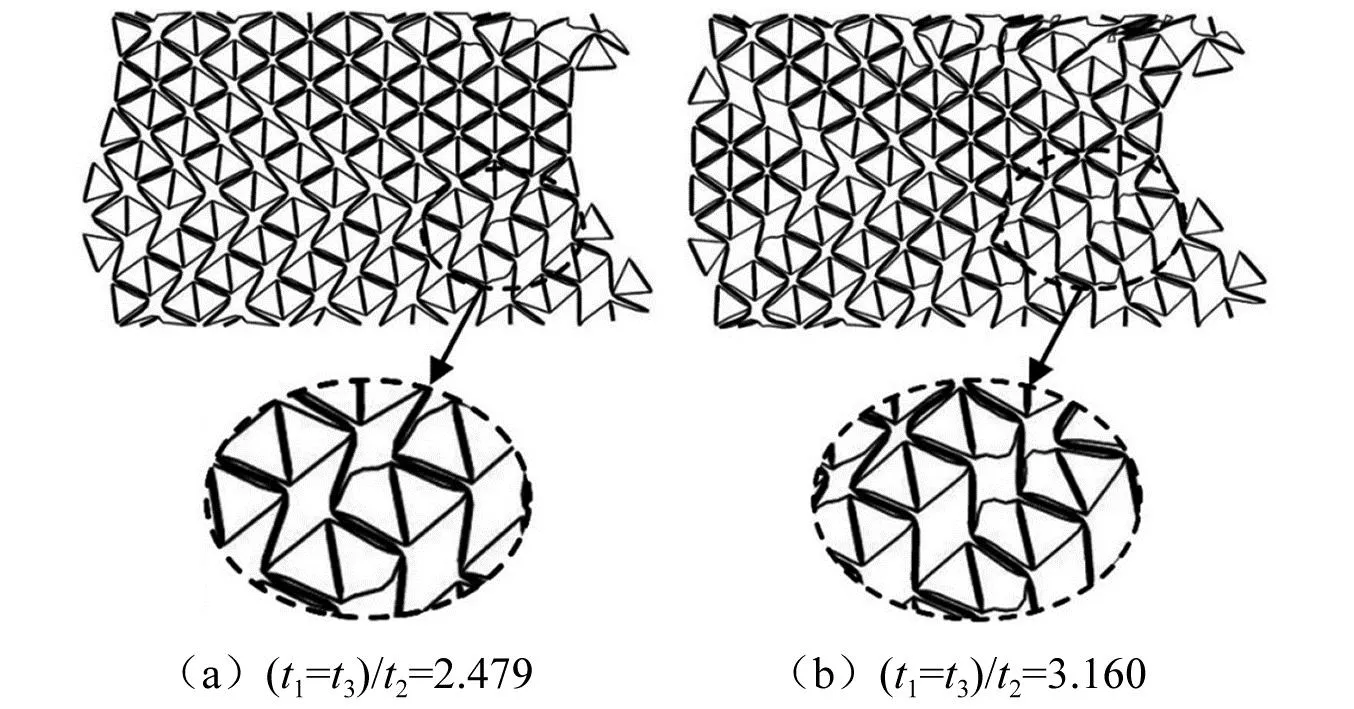
图14 非均匀壁厚STH的面内压缩局部变形图
此外,初始刚度Ef随着(t1=t3)/t2的增大逐渐增大,而强化刚度Ec随(t1=t3)/t2的增大先增大再减小,最终完全消失,如图15所示。当(t1=t3)/t2≤1.575时,由于STH整体平稳的收缩变为三角形格栅结构且胞壁W3壁厚增大使得承载能力增强,因此强化刚度Ec随着(t1=t3)/t2的增大逐渐增大。当1.575<(t1=t3)/t2≤2.479时,由于胞壁W2过早发生塑性屈曲使得STH变为三角形格栅结构时不稳定,且等效壁厚2t1+t2明显减小,因此其强化刚度Ec随着的(t1=t3)/t2的增大逐渐减小。其中,当(t1=t3)/t2≥2.05后,STH的强化刚度Ec甚至小于均质壁厚STH-30-1的强化刚度。当(t1=t3)/t2≥2.479后,由于三角形胞壁的过早塑性屈曲变形,使得STH的局部塑性变形显著,且三角形格栅结构的等效壁厚明显减小,因此强化刚度Ec消失。由此可得,改变(t1=t3)/t2的参数可以进一步地实现对STH不同阶段压缩刚度调控的目的。
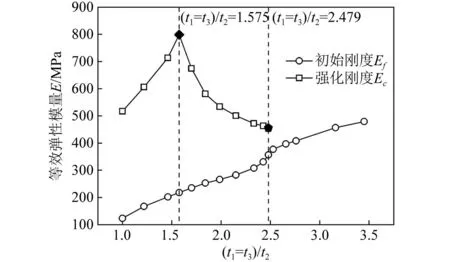
图15 不同(t1=t3)/t2的STH的初始刚度及强化刚度
3.3 胞壁角对刚度可调控影响
胞壁角α对STH的力学性能具有显著的影响,不同胞壁角的STH的面内压缩应力-应变响应如图16所示。改变胞壁角不仅影响STH的初始刚度和强化刚度的大小,同时影响强化刚度对应的应变。随着胞壁角α的增大,初始刚度Ef先减小再增大,呈开口向上的抛物线变化。当α<25°时,胞元的整体尺寸减小且胞壁连接处的重叠增大,使得内凹胞壁的有效长度减小,从而导致初始刚度随着胞壁角α的减小逐渐增大。当α≥25°时,内凹胞壁逐渐趋于垂直,内凹胞壁的弯曲挠度减小且支撑刚度明显增大,初始刚度随胞壁角α增大迅速增大。强化刚度Ec随着胞壁角α的增大呈先增大再减小的变化模式,如图17所示。当α≤30°时,STH能够均匀地收缩变为三角形格栅结构,且垂直胞壁的有效长度减小,三角形格栅结构的承载能力显著提高,其强化刚度Ec随胞壁角α的增大逐渐增大。当30°≤α≤60°时,靠近上下支撑板的胞元受摩擦效应影响无法充分的横向收缩,从而导致三角形格栅结构发生局部塑性变形,且这种非均匀的局部变形随胞壁角的增大越来越明显。因此,STH变为三角形格栅结构后的承载能力不足,其强化刚度Ec随胞壁角α的增大逐渐减小。然而,当α>60°后,垂直胞壁的长度非常短,面内压缩载荷下等效壁厚增大的倾斜胞壁更早地发生塑性屈曲,然后垂直胞壁发生塑性屈曲,三角形格栅结构呈现混合塑性屈曲变形模式。因此,STH的强化刚度Ec消失,应力-应变曲线呈迅速增大的变化模式。
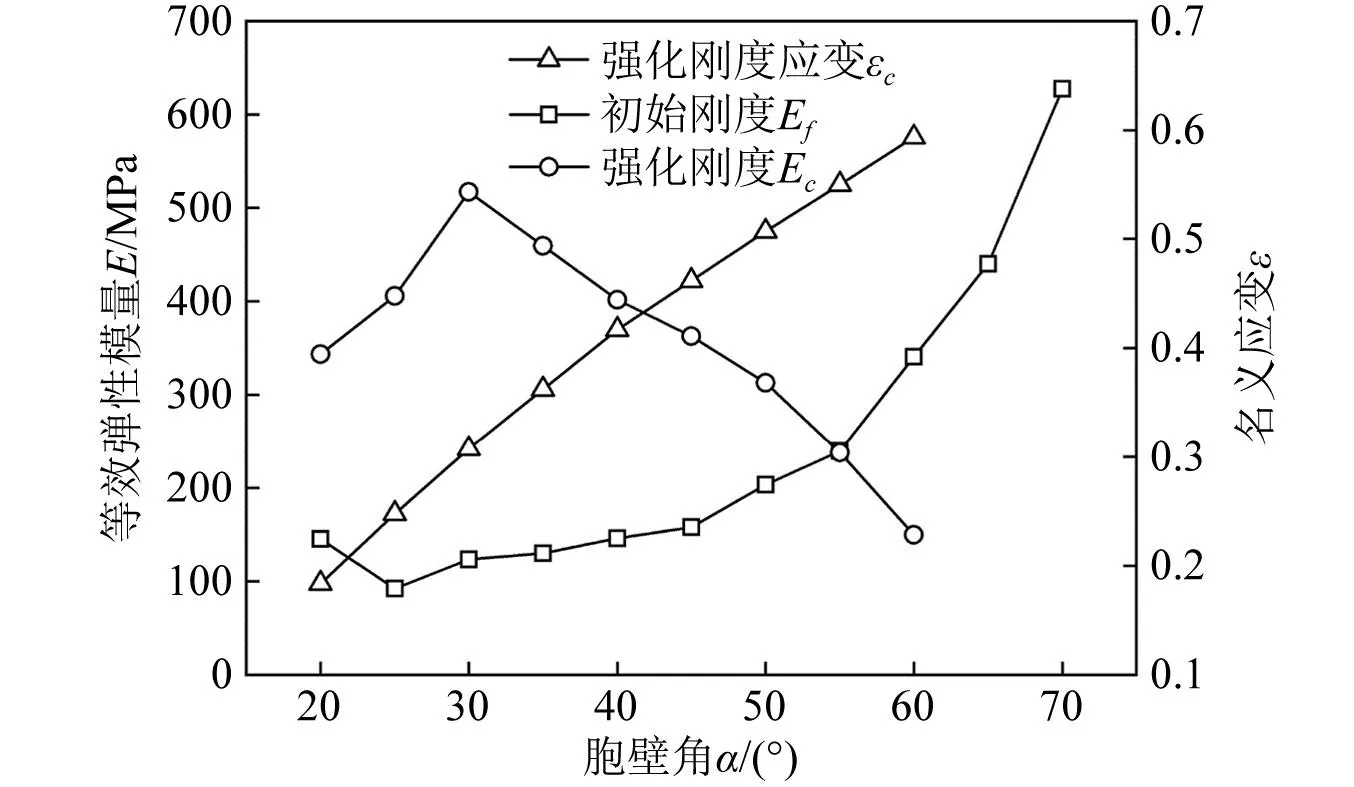
图16 不同胞壁角的STH的面内压缩应力-应变响应
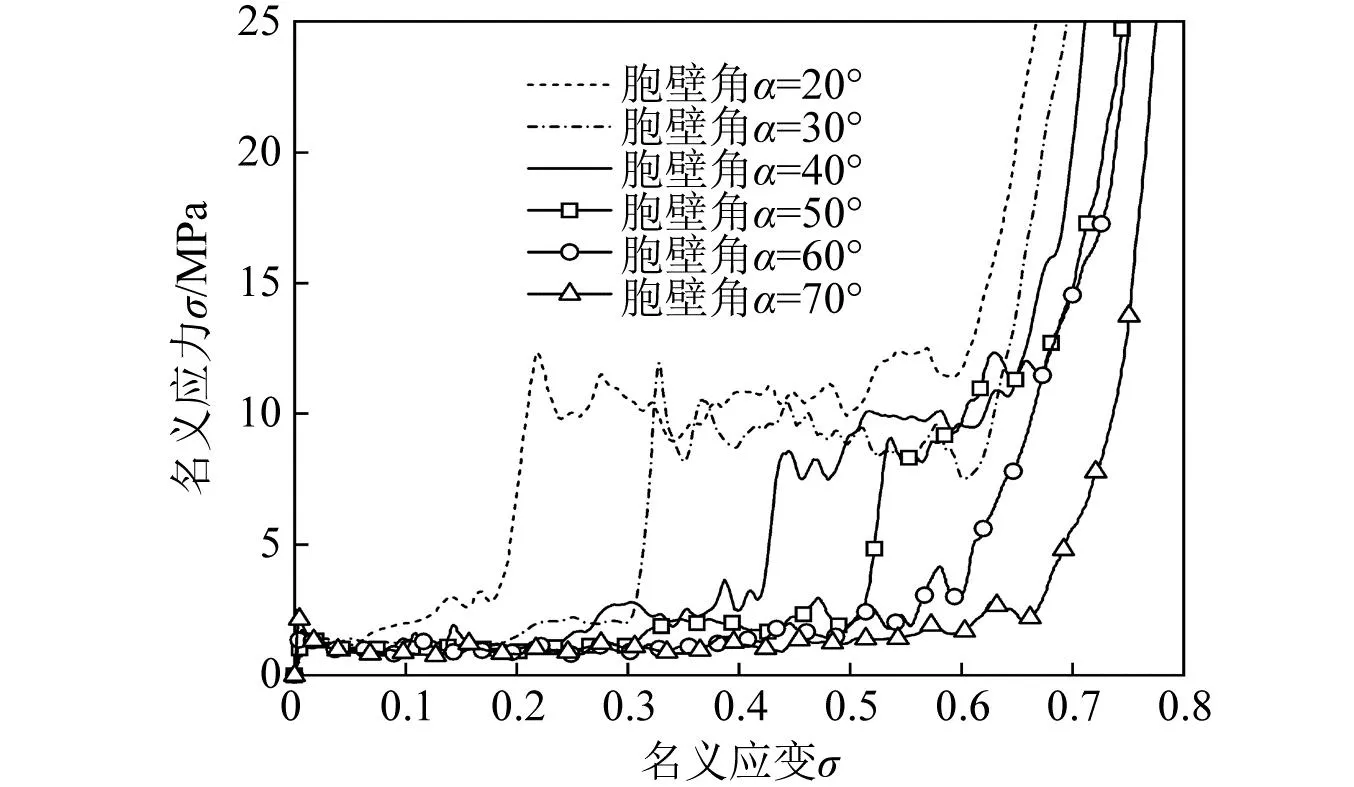
图17 不同胞壁角的STH的初始刚度及强化刚度
3.4 与其他负泊松比结构对比
调整STH的不同类型胞壁厚度比得到三种新构型[(t1=t3)/t2=1.0、t1/(t2=t3)=2.3、(t1=t3)/t2=1.575],并与相对密度相同的星型-箭头结构(star-arrowhead honeycomb,SAH)、内凹-星型结构(re-entrant star-shaped honeycomb,RSH)和星型结构(star-shaped honeycomb, SSH)的压缩刚度进行对比,如图18所示。
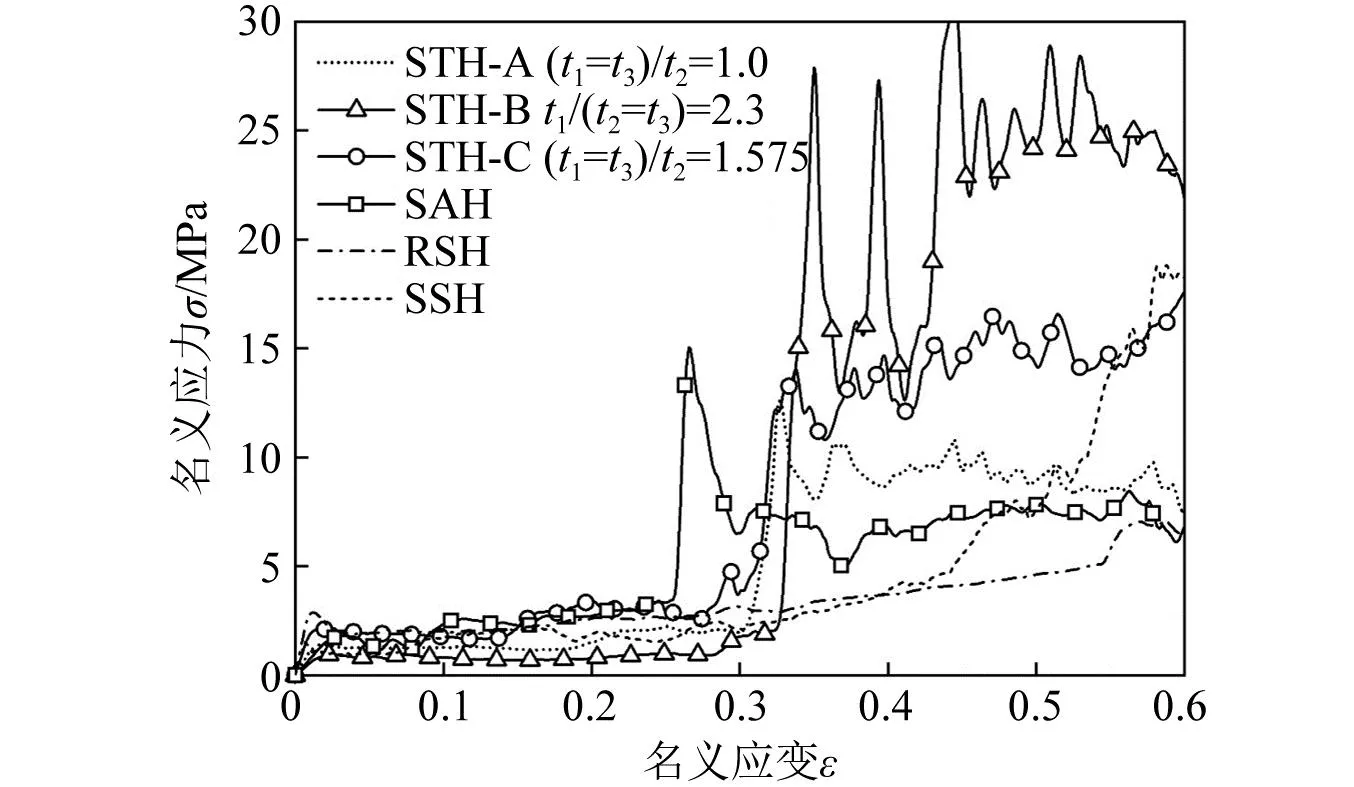
图18 不同负泊松比结构压缩刚度对比
由于相同相对密度条件下RSH和STH-C的内凹胞壁W3的厚度较大,其初始刚度比其他负泊松比结构更大。然而,RSH和SSH在变为新结构后仍容易发生塑性屈曲,其在面内压缩载荷下几乎无明显的强化刚度阶段。SAH在面内压缩载荷下逐渐变为新结构,应力-应变曲线呈现出明显的强化刚度阶段,且强化刚度Ec比STH-A和STH-B更优异,但初始刚度Ef明显小于STH-A和STH-B。此外,利用不同类型胞壁结构厚度的控制可以实现STH的初始刚度Ec和强化刚度Ef同时增强的效果。
由STH的局部变形分析可得,垂直胞壁W1在塑性坍塌时具有优异的承载能力,胞壁W1的塑性坍塌是在STH的第二变形阶段且与其他胞壁结构的变形不存在明显的耦合关系。因此,控制胞壁W1的厚度可有效地提高STH-C的强化刚度和平台应力,与SAH相比具有更优异的强化刚度和平台应力。由此可得,STH中的垂直胞壁不仅提高了结构的变形稳定性及负泊松比效应,且为STH的力学性能调控创造了条件,可显著地提高其强化刚度及能量吸收性能,与其他新型负泊松比结构相比具备更优异的力学调控性能及调控效果。
3.5 强化刚度应变
由上述分析可得,强化刚度应变受胞元微观结构参数的影响,其大小主要由胞元的几何结构变化决定。在面内压缩第一变形阶段,仅内凹胞壁发生塑性屈曲,并诱导胞元收缩变为三角形格栅结构,如图19所示。其中强化刚度应变,即星型-三角形变为三角形格栅结构时对应的应变。通过胞元变形前后几何结构的变化即可推导强化刚度应变的表达式。

图19 胞元变形前后示意图
由图1的结构几何参数图可得,初始状态时,单个胞元的高度H0=2lcosθ。胞元变为三角形结构后,其高度变为Hc,高度减小了ΔH=H0-Hc。其中,Hc主要由三角形结构垂直胞壁的高度h和胞壁重叠后的高度2Δh组成,即Hc=h+2Δh,如式(1)所示
Hc=2[lsinθ+(t2+t3)cosθ]
(1)
由此可得,强化刚度应变εc为
(2)
基于式(2)绘制不同结构参数的STH的强化刚度应变如图20所示。利用数值模拟结果对式(2)的强化刚度应变进行对比验证。胞壁角α≤40°时,强化刚度应变的解析公式与数值模拟结果具有较高的一致性。胞壁角α>40°后,与刚性板接触的胞元受摩擦约束的影响使其发生局部收缩变形,胞元未呈现出稳定的横向收缩变形模式,其对应的强化刚度应变与式(2)结果相比略小。3.3节中已系统地分析了胞壁角α对强化刚度应变的影响,强化刚度应变随胞壁角α增大呈近乎线性增大。胞壁厚度t2和t3的增大使得胞壁重叠高度Δh增大,相对应的可压缩空间减小,强化刚度应变εc减小。此外,对比胞壁厚度和胞壁角对强化刚度应变的影响可得,胞壁角的变化对强化刚度应变的影响更显著。

图20 不同结构参数的STH的强化刚度应变
4 结 论
针对星型-三角形负泊松比结构,利用面内压缩试验及数值模拟,研究了非均匀壁厚STH的面内压缩初始刚度及强化刚度的可调控特性,得到如下结论:
(1) 面内压缩载荷下,STH的内凹胞壁旋转收缩驱使其变为三角形格栅结构,其应力-应变曲线呈现出2个线弹性阶段,且强化刚度比初始刚度显著提升,压缩刚度可随压缩应变的增大自我调控增大。
(2) 与均匀壁厚STH结构相比,增大内凹胞壁和垂直胞壁的厚度可同时提高其初始刚度及强化刚度。总质量不变条件下,内凹胞壁与垂直胞壁厚度增大23.5%,其初始刚度Ef和强化刚度Ec分别增强了63.82%和37.89%。
(3) STH的初始刚度Ef随(t1=t3)/t2的增大逐渐增大,强化刚度Ec随(t1=t3)/t2的增大先增大再减小。当(t1=t3)/t2=1.575时,强化刚度Ec达到峰值,然后逐渐减小;当2.479<(t1=t3)/t2时,强化刚度Ec消失,应力-应变曲线呈阶梯式增大的变化过程。
(4) STH的初始刚度Ef随胞壁角的增大呈开口向上的抛物线式变化,α=25°时为极小值;强化刚度Ec随胞壁角的增大先增大再减小,最终强化刚度Ec消失。其中,α=30°时的强化刚度Ec最大,而α>60°后的应力-应变曲线无第二线弹性阶段,强化刚度Ec消失。此外,强化刚度应变随胞壁角的增大近乎呈线性增大。
基于星型-三角形结构面内压缩载荷下的刚度自调节特性,控制不同类型胞壁厚度的分布及胞壁角可实现对其初始刚度、强化刚度及强化刚度应变的调控,与其他新型负泊松比结构相比具有更优异的力学调控性能及调控效果。

