一类顺向软弱夹层下伏于坡脚边坡的抗滑稳定分析

温仁节,王 瑶,宋 勇,陈启豪

(四川水发勘测设计研究有限公司,成都 610072)

0 前言

当岩质边坡的软弱夹层产状与坡面结构呈顺向结构时,开挖边坡稳定问题尤为突出[1]。对于软弱夹层倾角小于坡面倾角的边坡,随顺向软弱夹层空间位置不同,其在开挖坡面出露或下伏于坡脚[2]。

当软弱夹层切脚出露于坡面,如图1所示,此时边坡的失稳模式为软弱夹层以上岩体ABC沿软弱夹层滑动,边坡抗滑稳定安全系数可由下式计算[3]：

图1 软弱夹层出露于坡面

(1)

式中,G为单宽岩体自重;θ为软弱夹层倾角;φ为软弱夹层内摩擦角;c为软弱夹层黏聚力;L为滑动面长度。

如图2所示,当软弱夹层下伏于坡脚,边坡失稳模式判别变得困难。从边坡结构分析,软弱夹层仍是潜在滑面的一部分,但滑面剪出位置不确定。从边坡受力分析,坡脚岩体受到夹层以上岩体传递的不平衡推力最大,而坡脚距离软弱夹层最近,岩体应力明显大于其他部位,是边坡失稳的潜在剪出区,但滑面形状及剪出口仍不确定[4]。因此,有必要依托数值模拟,对此类边坡进行弹塑性分析,探究边坡失稳模式,并据此给出合理的边坡极限平衡分析方法。

图2 软弱夹层下伏于坡面

1 边坡抗滑稳定数值模拟

1.1 计算模型

计算依托实际工程中的基坑开挖边坡,边坡级别2级,基坑长200 m,取单宽岩体进行分析,计算网格如图3所示。边坡岩体为砂岩,下伏一条泥化夹层,网格剖分时将夹层厚度适当加厚至0.5 m,以便网格剖分,并将软弱夹层网格加密以提高模拟精度。边坡岩体物理力学参数见表1。边坡材料本构模型选取摩尔-库伦模型。计算约束边坡左右前后及底面法向位移。

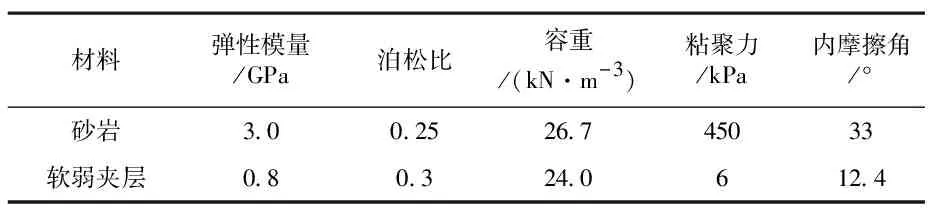
表1 边坡岩体物理力学参数

图3 边坡计算网格

1.2 开挖边坡应力变形结果

数值模拟先按岩体自重生成初始地应力场,并将位移和速度清零,再模拟开挖边坡临空面以上岩体。数值模拟表明该边坡变形收敛,开挖边坡位移及大主应力结果分别见图4、图5。由图4、图5可知,边坡开挖后总体发生卸载回弹,受软弱夹层影响,其上岩体位移明显大于其下岩体;坡脚因受坡面转折和软弱夹层影响,产生应力集中,最大主应力达1.16 MPa,是边坡失稳的潜在剪出区。

图4 开挖边坡位移等值线(单位：m)

图5 开挖边坡大主应力等值线(单位：Pa)

1.3 边坡抗滑稳定模拟

边坡抗滑稳定计算采用强度折减法,该法将岩体内摩擦角和黏聚力分别除以系数K后,进行稳定计算,通过不断加大K值,直至边坡失稳,此时的K值即为边坡抗滑稳定安全系数,边坡失稳判据为塑性区贯通或变形不收敛。计算得边坡抗滑稳定安全系数Fs=1.741,大于2级边坡施工期允许安全系数1.20。

强度折减后边坡位移等值线见图6,由图6可知,边坡潜在失稳区为夹层以上和坡脚岩体;边坡位移矢量见图7,坡脚以上失稳岩体位移矢量方向与软弱夹层平行,坡脚位移矢量方向从右下偏转至右上。

图6 强度折减边坡位移等值线(单位：m)

图7 强度折减边坡位移矢量示意

强度折减后边坡大主应力见图8,坡脚应力集中明显,最大值为1.47 MPa,较强度折减前增加了0.31 MPa;边坡塑性区分布见图9,塑性区沿软弱夹层发育,在坡脚贯通,呈“K”型,为剪切塑性区。

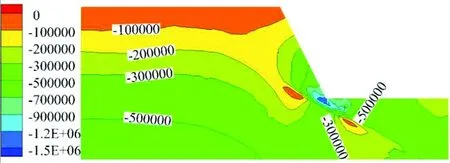
图8 强度折减边坡大主应力等值线(单位：Pa)

图9 强度折减边坡塑性区分布

综合图6-图9,不难发现,这类顺向软弱夹层下伏于坡脚的开挖边坡,潜在失稳滑面沿软弱夹层发育,在坡脚转折后,从坡脚地基剪出。从边坡塑性区分布图分析,坡脚岩基受到上部不稳定岩体沿软弱夹层传递的不平衡推力,导致坡脚地基整体处于塑性状态,发生剪切隆起,其失稳机理是地基承载失效。

2 边坡极限平衡分析

数值模拟结果表明,软弱夹层下伏于坡脚边坡的失稳模式为地基承载失效。将坡脚平面以上岩体传递的不平衡推力视作地基荷载,则可通过地基极限承载力与不平衡推力的比值来度量边坡安全系数。地基极限承载时,坡脚岩体处于塑性状态,应同时满足塑性条件和平衡条件,若将地基视作无重介质,可通过特征线法,求解地基极限平衡状态偏微分方程组,得到地基极限承载力,即Prandtl-Reissner课题解[5],但这种处理与实际差异较大,加之软弱夹层的影响,偏微分方程组解析解不易求得。

若将软弱夹层视作倾向下游的坝基缓倾结构面,则此类边坡稳定与重力坝深层抗滑几近相似[6]。如图10所示,距离坡脚E水平长度L处,存在软弱夹层,类比重力坝深层抗滑计算方法,将边坡滑面简化为双滑动面。显然,双滑动面的一条为软弱夹层面AB,另一条滑面B剪出于坡脚基础C。结合图6,假定两组滑动面的交点B为坡面FE延长线与AB交点。

图10 边坡抗滑稳定分析计算

重力坝深层抗滑稳定常见计算方法有：抗力体极限平衡法、等安全系数法和不平衡推力法等。边坡抗滑稳定计算采用混凝土重力坝设计规范附录C的等安全系数法,按抗剪断强度公式计算。

边坡不存在坝体垂直荷载W和水平荷载H;基坑施工期地下水位远低于基坑,滑面AB扬压力U1、滑面BC扬压力U2、BD面扬压力U3为0;偏于安全考虑,BD面上的作用力Q与水平面的夹角U2取0,岩块ABDEF的抗滑安全系数由式(2)计算：

(2)

岩块BCD抗滑安全系数由式(3)计算,

(3)

以图3边坡为例,L=2.36 m,α=28°,坡高h=15 m,Q、β待定,滑动面物理力学参数见表2。取单宽岩体,通过简单的平面几何关系,即可求得滑面AB面积A1=35.59 m2,岩块ABDEF自重G1=5 165.9 kN;滑动面BC面积及岩块BCD自重为β的函数。

表2 滑动面物理力学参数

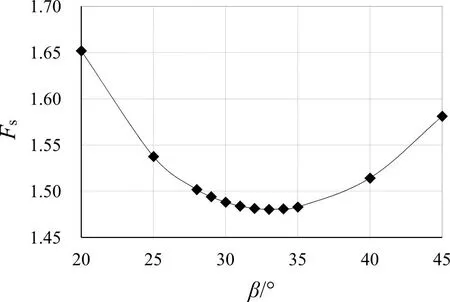
图11 β～Fs关系曲线

图12 β～Q关系曲线

3 结论

(1)顺向软弱夹层下伏于坡脚的岩质边坡失稳机理为地基承载失效;

(2)类比重力坝深层抗滑稳定计算,按等安全系数法计算的此类边坡抗滑稳定安全系数小于数值模拟结果,即等安全系数法更加保守。