多体非完全经典态的基于Affinity的关联测度

闫栋华,王银珠

(太原科技大学 应用科学学院,太原 030024)

在量子资源理论中,量子关联作为一种必要的物理资源已被广泛应用于量子计算的各个方面[1-8]。研究发现纠缠并不是唯一的量子关联,在复合量子系统中存在诸多形式的量子关联,包括量子失谐[9-11]、测量诱导的非局域性[12-14]、贝尔非局域性[15]、量子导引[16]等。深入刻画蕴含在量子态中的关联程度无疑具有一定的理论与实际意义。

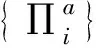
(1)

Affinity具有如下性质[17-18]:

(1)(非负性) 0≤A(ρ,σ)≤1,且A(ρ,σ)=1当且仅当ρ=σ.

(2)(酉不变性) 对任意酉算子U,有A(UρU+,UσU+)=A(ρ,σ).

(3)(单调性) 设Λ为完全正的保迹线性映射,则A(Λ(ρ),Λ(σ))≥A(ρ,σ).

最近,Muthuganesan.R和Chandrasekar.V K基于Affinity提出了两体量子态的测量诱导的非定域性[19],其定义为:

(2)

受此启发,本文主要考虑多体复合量子系统,给出了多体量子态基于Affinity的量子关联测度,其可以识别多体非完全经典态,并证明了该关联测度满足量子关联度的必要性质。

1 基本定义与主要结果

本文主要讨论多体复合量子系统,设H=H1⊗H2⊗…⊗Hm,dimH=d<+∞,H中所有完全经典态组成的集合记为SF-C(H).下面首先给出如下定义。

定义1设H=H1⊗H2⊗…⊗Hm,dimHi=di<+∞,ρ∈S(H),令

(3)

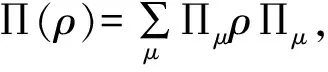
接下来证明基于Affinity的量子关联度是定义良好的,即其满足关联测度必要的一些物理性质。

定理1设H=H1⊗H2⊗…⊗Hm,dimHi=di<+∞,ρ∈S(H),则CA(ρ)≥0且CA(ρ)=0当且仅当ρ∈SF-C(H).

证明由CA(ρ)的定义,其非负性显然。

另外,若CA(ρ)=0,则存在,使得根据文献=1⟺ρ=σ,可得ρ=(ρ),即故ρ∈SF-C(H).反之,如果ρ∈SF-C(H),显然有CA(ρ)=0.

定理2设H=H1⊗H2⊗…⊗Hm,dimHi=di<+∞,ρ∈S(H),令U=U1⊗U2⊗…⊗Um,Ui∈Hi为Hi上的酉算子,则CA(UρU+)=CA(ρ).

证明根据文献[17],酉变换不改变量子态间的Affinity,即

A(UρU+,UσU+)=A(ρ,σ),

故

CA(UρU+)=CA(ρ).

定理3设H=H1⊗H2⊗…⊗Hm,dimHi=di<+∞,ρ∈S(H),Λ表示一个完全正保迹线性映射(CPTP),则CA(Λ(ρ))≤CA(ρ).

证明根据文献[18],在CPTP映射Λ下,A(ρ,σ)是单调的,即A(Λ(ρ),Λ(σ))≥A(ρ,σ).

从而

A(Λ(ρ),[Λ(ρ)])≥A(ρ,(ρ)),

故

由CA(ρ)的定义,显然有

CA(Λ(ρ))≤CA(ρ).

定理4设H=H1⊗H2⊗…⊗Hm,dimHi=di<+∞,ρ∈S(H),则CA(ρ)相对于输入态是凸的,即

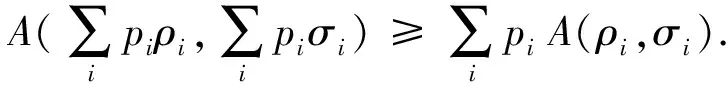
这里显然有

A(∑ipiρi,(∑ipiσi)≥∑ipiA(ρi,(ρi)),

而

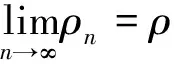
证明由定义得出:

2 结论

本文定义了一个新的关联测度——多体量子态基于Affinity的关联测度,并证明了其具有非负性、酉不变性、凸性、单调性以及连续性。该关联测度可以用来探测给定量子态是否为完全经典态,对进一步识别量子态具有一定的理论意义。