一类分数阶时滞微分系统的精确解及Hyers-Ulam稳定性

邬忆萱，寇春海

(东华大学 理学院, 上海)

分数阶微积分是广义微积分的一个分支[1]。作为整数阶微积分的一种推广,分数阶微积分主要研究任意阶微积分理论及其应用。分数阶微分算子为非局部算子,具有记忆性的特征,能很好地反映具有遗传特性的现象和过程,因此分数阶系统的研究引起了较广泛的关注[2-3]。在多种分数阶微积分定义中,Riemann-Liouville定义和Caputo定义的使用最为广泛。

分数阶微分方程的发展自然带来了对其稳定性问题的研究。Ulam[4]最先提出了同态稳定性的问题。Hyers[5]在此问题上有了突破性的进展,给出了相关稳定性定理。此外,Rassias 等[6]通过减弱柯西差分的条件,成功地推广了Hyers定理的结果,该研究结果引起了数学家们对泛函方程稳定性问题的关注[7]。Alsina等[8]将Hyers-Ulam稳定性的研究范围从泛函方程领域延伸到了微分方程领域,证明了一类一阶线性微分方程的Hyers-Ulam稳定性。这一基本结果目前已经被陆续推广到差分方程和脉冲微分方程等方向[9-10]。近年来,国内外学者研究了多种分数阶微分方程的Hyers-Ulam稳定[11-13],但关于分数阶时滞微分方程的Hyers-Ulam稳定性的研究还较为少见。

众所周知,时滞微分方程在自然科学的一些应用问题中时常出现。由于系统需要有限的时间来感知信息,然后像自动引擎一样做出反应[14-17],因此几乎所有涉及反馈控制的系统都会存在时滞。文献 [18-20]针对n维时滞线性微分方程提出了时滞矩阵函数的概念,并利用常数变易法分别研究了单、多时滞线性微分系统柯西问题解的表示。在此基础上,Li等[21]用类似方法研究了Riemann-Liouville分数阶单时滞微分方程的精确解表示。Liu等[22]考虑了Caputo分数阶单时滞微分方程的精确解及Hyers-Ulam稳定性。值得注意的是,多时滞系统的许多研究结果都是建立在系数矩阵可交换的前提下的[23-24]。Pospíšil[25]提出了不可交换矩阵的多项式定理,讨论了具有多个时滞和不可交换系数矩阵的一阶微分方程的精确解表示。Elshenhab等[26]采用类似方法,研究了二阶多时滞微分方程的精确解表示。

受此启发,本文研究一类具有多个时滞的Caputo分数阶线性微分方程,在不要求系数矩阵可交换的前提下,得到了系统的精确解表示,并研究了其有限时间内的Hyers-Ulam稳定性,建立了充分条件,将已有的整数阶研究成果推广到了分数阶微分系统。

1 预备工作

定义1[1]假设α∈C,Re(α)≥0。函数y(x)：[0,+∞)→R的α阶Caputo分数阶导数定义为

其中,

Caputo分数阶导数的下述性质被广泛地应用于分数阶微分方程。

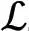
则有

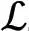
特别地,若1<α<2,则

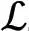
引理2[27]对于向量值函数φ(x),φ1(x),φ2(x)：R→Rn以及充分大的s,Laplace变换有如下性质成立：

1)对任意常数a、b,Laplace变换具有线性性,即

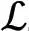
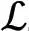
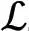
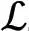
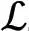
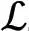
根据欧拉Γ函数和B函数的定义,得到下述结论。

引理3对任意常数a,b≥0及p,q>0,有如下等式成立。

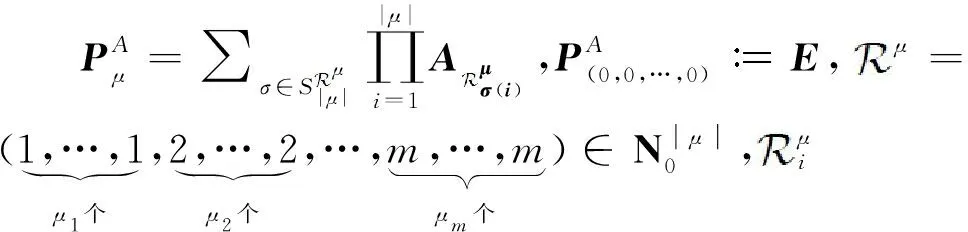
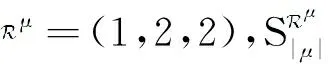
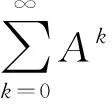
此外,本文研究的分数阶时滞线性方程如式(1)。

(1)

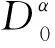
定义2假设常数K>0,任意ε>0,求得式(2)。

(2)

则称式(1)在I上具有“Hyers-Ulam稳定性(HUS)”,并称这样的常数K为该方程的“HUS常数”。

2 单时滞分数阶微分系统的精确解

假设式(1)中m=1,f(x)≡θ(θ为零向量),考虑单时滞线性微分系统的初始问题

(3)

其中,φ∈C2([-τ,0],Rn)。

定理1若式(3)的解y(x)及其α阶导数的Laplace变换均存在,则y(x)可表示为式(4)所示。

(4)

其中,

其中k∈N+。

证明：根据引理1和引理2,对式(3)方程两端分别作Laplace变换,可得

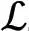
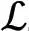
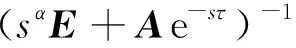
下面分别对M1、M2、M3作Laplace逆变换。

1)由于

结合引理5得

2)由于

对M1作Laplace逆变换的计算,可得

3)根据

再结合引理2可得

综上所述,x>0时,式(3)的解具有如下形式：

推论1定理1中建立的时滞矩阵函数Sα(x)和Cα(x)具有如下性质：

2)Sα(x)和Cα(x)均是方程(3)的解。

证明：1)对任意k∈N+,kτ≤x<(k+1)τ时,

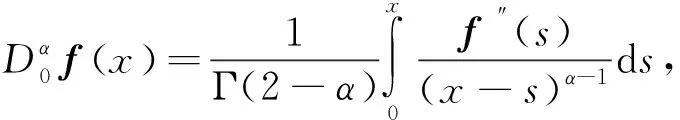
同上可得

综上知推论成立。

采用常数变易法求解单时滞常微分系统,得到了相应的时滞矩阵函数[22],由本文推论1可以看出,虽然与文献[22]中使用的直接法不同,但本文使用Laplace变换方法求解单时滞分数阶微分系统,得到的时滞矩阵函数依然具有文献[22]中时滞矩阵函数类似的性质,同样能够构成该齐次方程式(3)的基础解系,从而将已有的研究成果推广到分数阶微分系统。

3 多时滞分数阶微分系统的精确解

考虑多时滞非齐次分数阶微分系统

(5)

式中：f为[0,∞)→Rn指数有界;φ∈C2([-τ,0],Rn)。

定理2若式(5)的解y(x)及其α阶导数的Laplace变换均存在,则y(x)可表示为如式(6)。

(6)

其中,

证明：根据引理1和引理2,对式(5)方程两端作Laplace变换可得到

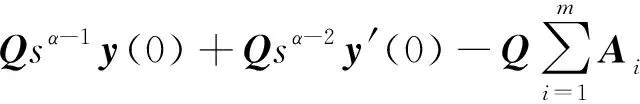
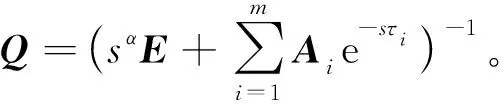
又由引理4和引理5,

下面分别对H1、H2、H3、H4作Laplace逆变换。

1)由于

故

2)由于

作Laplace逆变换计算可得

3)由于

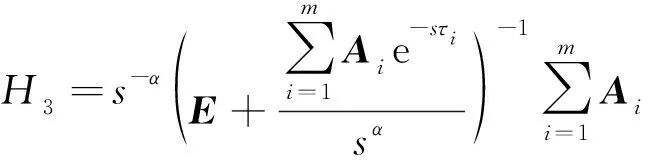
可求得

则

4)由

可得

综上所述,x>0时,式(5)的解具有如下形式：

推论2若A1,A2,…,Am为n×n可交换非零实矩阵,即AiAj=AjAi,1≤i≠j≤m,则式(5)的解可表示为

其中,

证明：结合引理4和AiAj=AjAi,易得

将上式代入定理2中,可知结论成立。

在系数矩阵可交换的前提下得到相应的时滞矩阵函数及多时滞系统的解[24],由推论2可知,本节的结果同样适用于系数矩阵可交换的情形,并且对应的形式与文献[24]中建立的时滞矩阵函数类似。

定理3

是系统

(7)

的解。

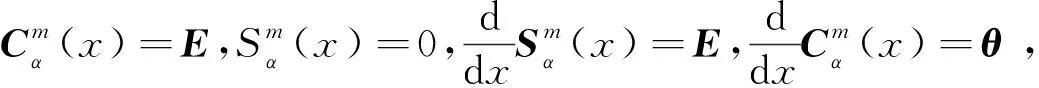
上述定理表明式(6)确为式(5)的解。

4 Hyers-Ulam稳定性

定理4方程式(1)在有限时间[0,T]内具有Hyers-Ulam稳定性。

(8)

则‖Z(x)‖≤ε。对式(8)两端分别作Laplace变换可以得到：

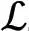
即

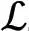
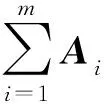
由定理2可知方程式(1)存在形如式(6)的解,设此解为y(x),则

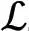
则有

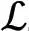
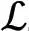
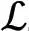
5 示例

例1考虑系统

(9)

其中,

其中,k∈N+。

例2考虑系统

(10)

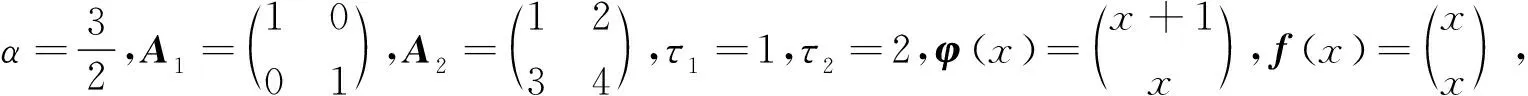
则根据推论2的结论,可以得到系统的解为

其中,

6 结 语

本文利用新的时滞矩阵函数和Laplace变换,在α∈(1,2)时,研究一类具有多个时滞的n维线性α阶微分系统的解的表示。本文在不要求系数矩阵可交换的前提下,利用不可交换矩阵的多项式定理,研究了多时滞系统的精确解并进行了代入验证。其中得到的时滞矩阵函数与整数阶微分系统、单时滞系统与已有研究结果中时滞矩阵函数具有类似正余弦性质,精确解的形式也囊括系数矩阵可交换的情形。利用已求得的精确解,采用Laplace变换,得到方程在有限时间[0,T]内具有Hyers-Ulam稳定性的结论。由此,本文将整数阶多时滞系统精确解的研究推广到了分数阶领域,除Caputo分数阶定义外,还有多种分数阶定义的情形可以考虑。