基于GA-BP神经网络和改进粒子群算法的碰撞射流和冷却顶板复合空调系统优化

齐贺闯，叶 筱，2，高延峰，2，亢燕铭，钟 珂

(1.上海工程技术大学 机械与汽车工程学院,上海;2.上海市大型构件智能制造机器人技术协同创新中心,上海;3.东华大学 环境科学与工程学院,上海)

高效气流组织是暖通空调领域的重点研究方向,其不仅对改善室内热环境、提高室内热舒适度和空气质量具有重要作用,还能够实现高品位负荷向低品位负荷的转移,进而为提高低品位能源利用率提供可能[1]。随着“双碳”目标的提出,研究和开发具有高效气流组织的空调系统的呼声越来越高。

碰撞射流通风(impinging jet ventilation, IJV)是一种典型的下送风通风方式,其通风原理是送风气流以较高的动量从房间下部垂直射出,撞击地面后在残余动量作用下沿着地板水平扩散,并在地板上方形成“空气湖”,回风则从位于房间上部的回风口排出[2]。研究[3]表明,供冷时IJV具有与置换通风(displacement ventilation, DV)相似的分层气流形态,能够实现节能以及提供良好室内舒适度和空气质量的目标。但与DV不同的是,IJV可用于供暖,并且供暖时相比混合通风(mixing ventilation, MV)能够节约20%以上的能耗。IJV独特的气流组织使其有望替代MV和DV。然而,由于IJV将送风气流直接送至人员活动区,为了保证人员舒适度,须将送风速度和送风温差控制在一定范围[4],这导致其负荷承担能力有限。Hu等[5]研究发现,IJV供冷时的最大负荷承担量仅为50 W/m2左右,仅能满足一般住宅或小型办公建筑的需求。而我国多数公共建筑(航站楼、候车厅、展厅等)通常具有大面积玻璃幕墙,这导致其房间负荷可达100 W/m2,甚至更高[6]。为了拓展IJV在此类高负荷空间场所的使用,必须附加额外的供冷或供热设备,这些设备又被要求对IJV气流组织的影响足够小。

顶板辐射(radiant ceiling, RC)空调是一种以辐射换热为主的空调方式,因其具有对流换热量小的特点[7],故不会影响IJV的流型。此外,由于辐射空调不能提供房间所需新风,因此在使用时需要配备独立新风系统[8]。以往研究均是将RC与MV或DV结合使用,即MV/RC或DV/RC复合空调,但MV和DV自身的局限性,导致MV/RC仍存在节能性差、热舒适度和空气质量不高的缺点[9],DV/RC供暖时存在严重的冷热量抵消问题[10]。根据IJV的气流组织特点,将其与RC结合(即IJV/RC复合空调)能够避免上述传统复合空调存在的问题,并达到相辅相成、扬长避短的目的。然而,至今尚无关于IJV/RC复合空调的研究,在空调系统优化设计及运行控制等方面尚缺乏可靠的理论依据。

本研究以IJV/RC复合空调为研究对象,对其用于房间供冷时的运行性能进行优化研究。通过分析不同房间负荷条件下,设计变量如送风温度、送风速度、冷却顶板内表面温度等因素对室内热环境的影响,采用基于遗传算法的BP神经网络(简称GA-BP神经网络)建立复合空调运行性能评价指标的预测模型,并基于改进粒子群(PSO)算法对复合空调运行性能进行多目标同时优化,构建设计变量组合条件与房间负荷的最优匹配关系,以确保空调系统高效运行。

1 研究方法

利用CFD软件模拟IJV/RC室内热环境,采用GA-BP算法建立IJV/RC复合空调运行性能与设计参量之间的预测模型,在对不同工况下的运行性能进行预测的基础上,基于改进PSO算法进行多目标同时优化研究,建立IJV和RC各主要设计参量的最优匹配关系。

1.1 物理模型及边界条件

以一个房间尺寸为长x=9.0 m、宽y=5.8 m、高z=2.7 m的8人办公室为研究对象,房间的3D透视图如图1所示。碰撞射流通风系统的送风管道紧靠房间四角布置,送风口尺寸为0.3 m×0.3 m,送风口高度为0.6 m,两个排风口尺寸均为0.30 m×0.55 m,对称分布在天花板两侧。辐射冷板覆盖于天花板下方,尺寸为7.8 m×5.3 m,覆盖率为80%。为贴近实际,外墙上有一块尺寸为7.5 m×2.4 m的玻璃窗(见图1),窗墙面积比为0.74。

a—IJV送风口;b—IJV回风口;c—窗户;d—办公桌;e—电脑;f—坐姿人体模型;g—灯;h—冷却顶板。图1 物理模型Fig.1 Physical model

房间内布置有8个简化的人体模型(均处于坐姿状态)、8台电脑、2张桌子和9盏灯。人体模型、电脑和灯的散热量分别约为100 W/人、150 W/台和35 W/盏。由内部热源所引起的室内总冷负荷为2 315 W(对应冷指标为44.3 W/m2)。为分析IJV/RC在不同房间负荷条件下的室内热环境参数分布特性,模拟时通过调整外围护结构(包括外墙和窗户)和地面的热通量来获得所需的房间负荷。假定与所研究房间相邻的房间均为空调房间,除外墙和地面为热损失面外,其他墙面均设为绝热面。边界条件设置如表1所示。

表1 边界条件Table 1 Boundary conditions

1.2 数值计算方法及网格独立性验证

1.2.1 数值计算方法

采用SIMPLE算法对压力和速度项进行求解。关于模型的离散化,使用有限容积法离散Reynolds时均N-S方程;湍流模型采用RNGk-ε湍流模型[11];除压力项采用标准Standard格式外,其他项均选用二阶迎风格式。所有固体表面均设为无渗透和无滑移条件。辐射模型选择discrete ordinates(DO)模型[11]。由于本研究中的温度小于30 ℃,因此室内空气符合Boussinesq假设[12]。室内气流被认为是连续且不可压缩的,并遵循式(1)～(3)所示的质量、动量和能量守恒方程。

质量守恒方程：

(1)

动量守恒方程：

ρβgi(Tref-T)

(2)

能量守恒方程：

(3)

式中：ρ为空气密度,取1.225 kg/m3;Ui为xi方向的速度,m/s;Uj为xj方向的速度,m/s;p为空气压力,Pa;μ为空气层流动力黏度,根据空气温度变化而不同,在压强101.325 kPa、温度20 ℃的条件下取1.79×10-5kg/(m·s);β为空气热膨胀系数,3.66×10-3K-1;Tref为参考温度,取298.5 K;T为空气温度,K;h为空气定压比焓,取295.03 kJ/kg;λ为空气热导率,取0.024 2 W/(m·K);cp为空气定压比热,取1 006.43 J/(kg·K);SH为热源,根据室内热源强度确定,W。

1.2.2 网格划分及独立性检验

采用非结构化四面体网格进行网格划分,对室内温度和速度变化较快的热源表面、送回风口、外围护结构及地面附近区域的网格进行加密处理。网格数量的多少对模拟结果的准确性和计算成本有重要影响,为确定合适的网格数量,采用3种不同的网格尺寸(粗、中、细)进行网格无关性验证,并选取房间中心位置处的温度和速度沿房间高度的变化作为判别依据。图2给出了同一运行工况条件下,不同网格尺寸对应的室内温度和速度的模拟结果。

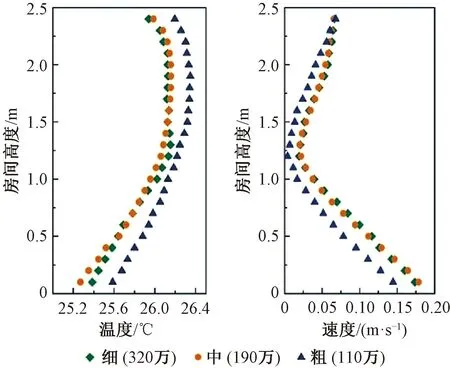
图2 网格无关性验证Fig.2 Grid independence test

由图2可知：当网格数从110万增加到190万时,网格数量的变化对不同位置处的温度和速度值均会产生一定的影响;当网格数由190万增加到320万时,网格数量的变化不再对模拟结果产生影响。因此选用网格数量为190万的模型进行后续的数值模拟,其最小网格尺寸为0.05 m,网格增长因子为1.1,网格质量系数为0.92。

1.3 CFD模型的合理性验证

采用文献[8]的试验结果验证本文中的数值计算方法的可靠性和合理性。试验中测试房间的尺寸为x×y×z=3.7 m×2.8 m×2.6 m,采用地板送风和冷却顶板复合系统。地板送风的送风口尺寸为0.25 m×0.25 m,排风口尺寸为0.84 m×0.24 m,位于侧墙上方。冷却顶板由11块金属辐射板组成,每块尺寸为0.6 m×1.2 m,覆盖率为76%。室内热源包括坐姿人体假人、电脑和灯。其中：坐姿假人用0.40 m×0.25 m×1.20 m的铁箱替代,铁箱内装有3个60 W灯泡,用于模拟人体散热,灯泡的功率调节范围为0～180 W;电脑用两个尺寸为0.4 m×0.4 m×0.4 m的铁箱子模拟,电脑内放置2个100 W灯泡,其功率可调范围为0～200 W;每个吊灯的功率为72 W,灯尺寸为0.2 m×1.2 m×0.05 m。房间内共布置7个测杆,每个测杆沿高度方向布置6个测点,距离地面高度分别为0.1、0.6、1.1、1.3、1.7、2.5 m。试验细节详见文献[8]。

所验证的工况：辐射板温度20 ℃,送风温度21 ℃,送风速度0.7 m/s,室内冷负荷430 W,外墙冷负荷430 W。图3给出了测杆2、测杆5和测杆7的温度和速度的模拟值与实测值对比。

注：θ=(ti-ts)/(te-ts),ti和te分别是测点温度和排风温度,ts为送风温度;U=vi/vs,vi和vs分别是测点速度和送风速度;Z=z/h,z和h分别是测点高度和房间高度。图3 实测值与模拟值对比Fig.3 Comparison of the measured and simulated values

由图3可知,对于大多数测点的温度和速度,本文的数值模拟结果与文献[8]的实测结果和模拟结果基本吻合。温度和速度的实测值与本文模拟值之间的最大相对误差分别为0.10和0.11,均出现在近地面区域。出现这一现象的原因有两方面：一是送风气流被直接送至房间下部,导致近地面区域湍流强度波动明显,而该区域的温度和速度受湍流模型和离散格式的影响较大,从而带来一定的计算偏差;二是速度值较小,存在一定的测量误差。总体而言,采用本文的数值计算方法能够得到较为准确的结果。

1.4 研究工况

选取送风温度ts、送风速度vs、辐射板温度tc、室内冷负荷Qc共4个因素作为研究变量。采用4因素3水平的全面试验设计。各设计变量位级的确定依据如下：

1)送风温度。由于IJV将送风冷气流直接送至人员活动区,为避免出现吹风感,IJV所允许的最大送风温差为4 ℃。夏季空调房间的设计温度为26 ℃,因此送风温度最低设定为22 ℃,每间隔1 ℃取1个位级。

2)送风速度。根据文献[4]的推荐值,IJV送风速度的变化范围取1～3 m/s,每间隔1 m/s为1个位级。

3)辐射顶板内表面温度。在夏季供冷季节,冷却顶板结露是复合空调系统的关键问题[13]。根据夏季室内空气露点温度变化范围(16～18 ℃),为防止顶板结露现象的发生,取顶板表面温度的最低值为20 ℃,最高值为22 ℃,另一个位级为21 ℃。

4)房间冷负荷。根据《实用供热空调设计手册》[6],房间冷指标的变化范围在90～200 W/m2。本文所涉及的IJV/RC复合空调旨在用于高负荷场所的供冷,故房间冷负荷变化范围取120～180 W/m2,每间隔30 W/m2为1个位级。

共对34(81)个工况进行数值模拟。选取吹风感RPD、头足温差Δt、工作区平均温度ta作为室内热舒适的评价指标,空气交换效率eACE作为室内空气质量的评价指标,具体计算方法见文献[3]。

1.5 GA-BP预测模型的构建

GA-BP预测模型的构建流程如图4所示。采用MATLAB R2020b建立GA-BP模型,并从1.4节中的81个工况中随机选取65个(80%)进行模型训练,剩余16个(20%)用于测试模型。选用ts、vs、tc、Qc作为模型输入,RPD、Δt、eACE、ta作为模型输出。输入层有4个神经元,隐藏层有15个神经元,输出层有3个神经元。利用遗传算法优化BP神经网络的权值和阈值[14],各主要参数的最终设定值为最大迭代次数100次,种群大小60,交叉概率0.70,变异概率0.01,最大训练次数1000次,学习率10-6,期望误差10-7。

图4 IJV/RC运行性能优化流程图Fig.4 Flow chart of the optimization of IJV/RC operating performance

采用平均绝对误差δMAE和绝对误差标准差δSDAE对所建立的GA-BP预测模型进行可靠性和准确性验证,计算公式为

(4)

(5)

式中：N为样本个数;Msim,i为CFD模拟值;Ppre,i为模型预测值。

1.6 改进PSO算法设计

PSO具有较快的计算速度和全局搜索能力[15],被广泛应用于组合优化问题[16-17]。但传统PSO的惯性因子和学习因子是固定的,易出现早熟收敛的情况。本文通过动态调整惯性因子和学习因子的组合来改进PSO,以平衡收敛速度。改进PSO的优化流程如图4所示。改进PSO通过更新粒子的速度和位置来寻找最优解[18],其速度和位置更新公式如式(6)所示。

(6)

式中：M为粒子群中粒子的总数,i=1,2,…,M;t为当前迭代次数;tmax为最大迭代次数;vi为粒子的速度;xi为粒子当前位置;r1,r2为(0,1)之间的随机数;pbest,i为第i代粒子群中的最佳适应度;gbest,i为所有粒子的最佳适应度。

优化IJV/RC的目的是获得较低的吹风感,较低的头足温差以及较高的空气交换效率。取RPD、Δt及1/eACE之和的最小值F,作为适应度函数代表对IJV/RC进行的一个定性的优化趋势,F值越小,意味着IJV/RC在该优化方向上表现越佳。适应度函数和约束条件如式(7)所示。

(7)

2 结果与分析

2.1 供冷模式下IJV/RC复合空调室内热环境分布特征

图5给出了房间负荷Qc为120 W/m2时,单一IJV和IJV/RC复合空调室内y=2 m平面上的温度流线分布。

图5 y=2 m平面上的流场和温度场分布Fig.5 Distributions of the velocity and temperature on the plane of y=2 m

从图5(a)可以看出,单一IJV即使在所允许的最大送风参数条件(ts=22 ℃,vs=3 m/s)下运行,室内工作区温度仍不能满足设计要求,且房间上、下部存在明显温差,人体头足温差高达5 ℃,远高于ASHRAE 55-2017规定的头足温差限值(3 ℃)。这证实了IJV不能在高负荷场所使用的结论。

图5(b)～(c)表明,当IJV与RC结合使用时,室内平均温度明显降低。这意味着IJV/RC比单一IJV具有较强的负荷处理能力。在辐射冷顶板的作用下,受室内热源加热的热羽流到达房间上部后被冷却,因密度下降而转为向下流动,使得室内垂直温度梯度大幅下降,从而提高室内舒适度。图5(b)～(c)中IJV/RC房间人体头足温差分别为1和4 ℃,相比图5(a)中单一IJV房间的头足温差均有所降低。但是,当房间负荷相同时,IJV的送风参数和冷却顶板内表面温度的匹配关系对室内热环境参数分布影响很大,若匹配不当,则室内仍将出现头足温差过大的风险(图5(c))。

2.2 GA-BP模型预测结果

图6为16组测试集模型预测值与CFD模拟值的对比。由图6可知,对于任一评价指标,测试集的模型预测值均能与CFD模拟值较好吻合。从表2可以看出,GA-BP模型预测的RPD、Δt、eACE、ta的δMAE和δSDAE值都很小,足以证实预测模型是可靠的。由此可见,本文所建立的GA-BP模型能够实现对IJV/RC复合空调运行性能的高精度预测[14]。

表2 GA-BP模型测试集的δMAE和δSDAE

图6 GA-BP预测值与CFD模拟值对比Fig.6 Comparison of values of GA-BP prediction and CFD simulation

2.3 设计变量的显著性分析

采用Spearman相关性分析探究各设计变量对IJV/RC复合空调系统运行性能的影响[19]。相关性分析结果如图7所示。从图7可以看出,ts、vs、tc、Qc与RPD的相关系数分别为-0.18、0.94、-0.11、-0.24,表明vs对RPD的影响最大,ts和Qc对RPD的影响相近,tc对RPD的影响最小;除vs外,其余设计变量均与RPD呈负相关。ts、vs、tc、Qc与Δt的相关系数分别为-0.05、-0.65、0.08,-0.06,表明vs对Δt的影响最大,且vs越大,Δt越小;tc、ts和Qc对Δt的影响可忽略不计。ts、vs、tc、Qc与eACE的相关系数分别为-0.12、-0.07、0.11、0.42,表明Qc对eACE的影响最大,且Qc越大,eACE越大;其次分别为ts和tc,vs的影响可忽略不计。ts、vs、tc、Qc与ta的相关系数分别为0.47,-0.66,0.15,0.49,表明vs对ta的影响最大,且vs越大,ta越小,ts和Qc对ta的影响相当,且均与ta呈正相关,tc对ta的影响最小。由上述分析可知,增大vs可使室内头足温差降低,但吹风感随之增大;增大tc有助于降低头足温差和吹风感,但工作区平均温度升高;为使工作区平均温度下降,可通过降低ts来实现,但室内空气质量变差。因此,为确定合理的设计参量匹配关系,需要对运行性能进行多目标同时优化研究。

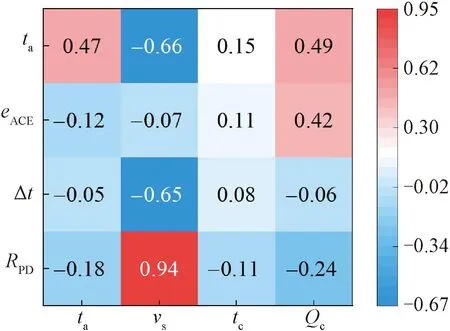
图7 Spearman相关系数Fig.7 Spearman’s correlation coefficient

2.4 改进PSO的优化结果

对于已经设计好的建筑,房间负荷是固定的,IJV/RC在运行过程中只能通过调节送风速度、送风温度、辐射顶板温度等设计变量来改变室内热环境。因此,采用改进PSO算法确定IJV/RC不同房间负荷下的最优设计变量组合,对IJV/RC复合空调系统的运行性能进行优化,优化结果如表3所示。表3所示的结果可为在供冷模式下IJV/RC的设计变量优化提供方向,以实现最佳的运行性能。

表3 不同房间负荷下的最优设计变量组合和对应的运行性能Table 3 Optimal combination of design variables and corresponding operating performance under different room cooling loads

2.5 验证试验

以Qc=140 W/m2为例进行优化结果验证。基于表3中该负荷条件下的最优设计变量组合,对IJV/RC进行CFD数值模拟,计算空调系统运行性能的评价指标。将CFD计算结果与模型优化结果进行对比,结果如表4所示。

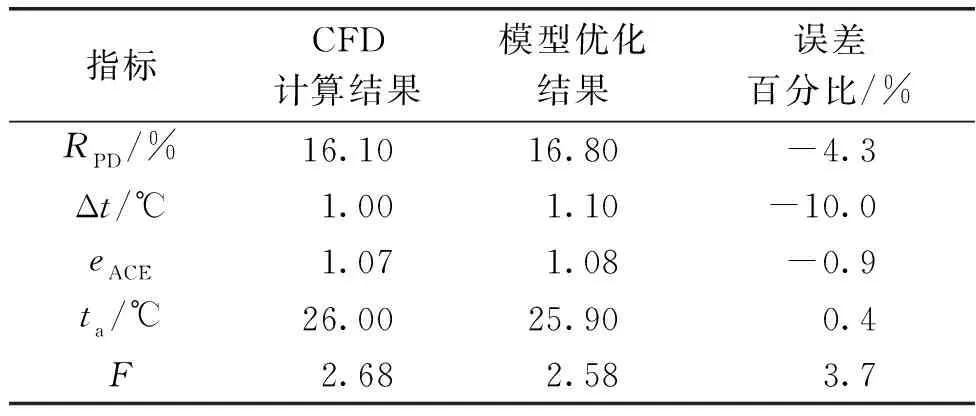
表4 验证优化结果Table 4 Verify optimized results

由表4可知,各项指标的CFD计算结果和模型优化结果间的误差均较小,最大不超过10%,处于可接受范围,并且适应度函数的误差仅为3.7%。验证结果表明,本文建立的基于GA-BP的改进PSO优化模型具有较高的可信度。

3 结 语

在对IJV/RC复合空调室内热环境进行数值模拟的基础上,基于GA-BP神经网络建立了IJV/RC复合空调运行性能的预测模型,分析了设计变量对运行性能的影响。结果显示,增大vs可使室内头足温差降低,但吹风感随之增大;增大tc有助于降低RPD,但ta升高;为使ta下降,可通过降低ts来实现,但室内空气质量变差。为确保IJV/RC兼顾提供良好室内热舒适和空气质量的双重目标,采用改进PSO算法对运行性能进行多目标同时优化,构建了设计变量组合条件与房间负荷间的最优匹配关系。本文的研究结果对IJV/RC运行参数的合理控制具有重要指导意义。