摄影测量中环状编码标靶识别与定位方法
李 恒,杨延竹,柳俊先,杨 肖
(东华大学 机械工程学院, 上海)
在三维摄影测量领域,为了提高相机标定、特征点立体匹配、数据拼接以及三维重建的准确性[1-2],使用编码标靶作为被测物体表面特征点。其中,圆环编码标靶具有仿射不变性、旋转平移不变性、易于识别等特点,因而被广泛应用。
空间平面上的圆在相机成像后易变为椭圆。由于透视投影的特性,圆心的投影点并不是椭圆几何中心,图像中单个椭圆可能对应着空间中多个平面圆,难以通过单个椭圆求解准确的中心,因此环状编码标靶中心精确定位与编码标靶解码是研究的关键。关于编码标靶中心的提取:孙丽君等[3]提出一种基于均值像素法的圆心亚像素提取方法,通过对编码标靶内像素点及像素坐标加权质心,求得其中心亚像素坐标,但未考虑透视变换的影响。陈天飞等[4]利用射影变换及RANSAC思想,计算椭圆圆心与射影变换后实际标靶标准圆心,并通过迭代的思想来优化射影变换矩阵,求得最优的椭圆圆心,但该方法迭代时间较长。Xie等[5]根据对偶二次曲线的几何特征提出经过任意两标志点的对偶矩阵,可得到一条穿过两圆圆心投影的特征向量,将同一个圆心投影后的多个向量叉乘,可得到任意圆圆心,但这需要平面内有非共线的3点才能求出圆心。关于编码标靶的解码:周申江等[6]通过仿射变换将椭圆变换为标准圆,然后进行编码标靶的解码,但此方法解码准确率较低;金滔等[7]在传统圆环编码标靶上添加3个定位符,既可以用于标靶定位,也可以增加标靶的数目,但图像较模糊时无法识别定位符;熊雪菲等[8]将编码标靶设计为定位层、起始层、编码层,既提高解码准确率,又增加了编码容量,但设计较复杂。
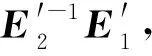
1 同心圆投影变换求解圆心
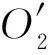
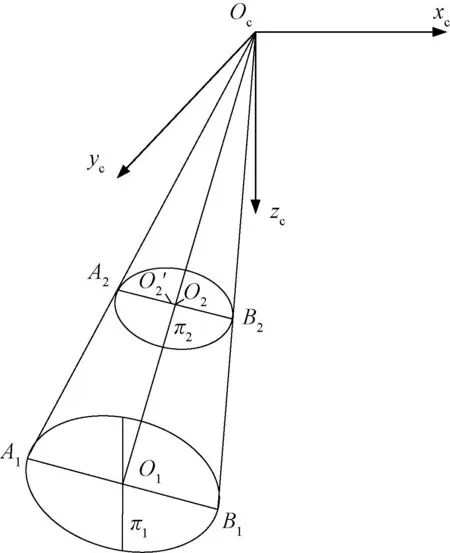
图1 圆的空间透视投影图Fig.1 Spatial perspective projection diagram of a circle
(1)
设
则由二次曲线投影变换公式一般表示形式E′=H-TEH-1可得[10],二次曲线变换后在图像平面上成像的椭圆方程如式(2)所示。
(2)
通过观察式(2)可发现:
1)若向量β属于正交于P3的平面,则E′1β=sE′2β(s为比例系数)。取该平面的两个基向量α1、α2,可得到E′1β1=sE′2β1和E′1β2=sE′2β2,即这两个基向量为矩阵E′2-1E′1的特征向量,两者对应的特征值均为s。


经进一步分析发现(2)中特征向量的含义,由H-1H=I可得H的第3个列向量h3正交于P1和P2。
(3)
另外,由点投影变换p′=Hp可得,原平面上原点经过投影变换后的坐标也为h3。
(4)

2 环形标靶编解码
本文采用具有明显特征的环形编码标靶进行编解码,如图2所示。对于左边不带编码信息的非编码标靶无编码信息,只能对其圆心进行定位,因此常用于相机的标定。而右边有编码信息的编码标靶不仅能对同心圆圆心进行定位,还能识别唯一的编码信息,常用于点云拼接和初步确立空间三维点坐标等[11]。

图2 非编码标靶与编码标靶Fig.2 Non-coded target and coded target
2.1 编码标靶设计
编码标靶的设计具备唯一性、便于识别以及数量充足等特点。Schneider等[12]设计的环形编码标靶应用较广泛,本文在该研究的基础上,设计了新的环状编码标靶(见图2)。该编码标靶由外部环状编码带与内部被12等分的编码标靶组成,其中,外部编码带用于标靶快速定位,内部编码标靶用于标靶识别。
此编码标靶同心圆直径由外向内分别为11、8、5 mm,每一等分编码标靶根据颜色的不同对应二进制的0或1。遍历编码标靶一周,将此12位二进制数对应的最小十进制作为此编码标靶的身份标识。
2.2 编码标靶提取及定位
采集编码标靶后,要对图像进行标靶提取,将符合特征的候选椭圆提取出来,以便后面的定位与解码,具体流程如图3所示。
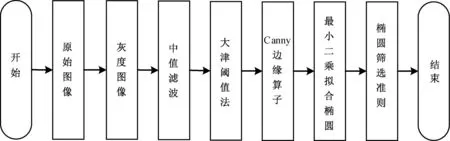
图3 编码标靶提取流程Fig.3 Encoded target extraction process
2.2.1 图像预处理
首先,将采集到的原始图像转为灰度图像,以减少图像原始数据,便于后续数据处理;其次,对灰度图采用中值滤波进行非线性处理,保留图像边缘信息,以实现在不损失图像细节的情况下保护图像边缘信息;再次,通过大津阈值法对图像进行二值化处理;最后,利用Canny边缘算子进行边缘提取。Canny边缘提取算子具有对梯度方向幅值进行非极大值抑制和可通过双阈值来进行边缘检测的优点,能够很好地检测边缘并进行连接。预处理前后的图像如图4所示。

图4 预处理前后图像Fig.4 Before and after pre-processing images
2.2.2 最小二乘法拟合椭圆
将提取到的边缘像素进行最小二乘法拟合椭圆,确定标靶中心位置坐标,以便进行下一步操作。
空间中的二次曲线如式(5)。
f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F
(5)
则目标函数为
(6)
若使G取得最小值,根据极值原理,需要满足式(7)。
利用WordCloud 制作词云时,一般经过三个步骤:一是使用wordcloud.WorldCloud 函数来设置词云对象的有关属性(或者说是参数);二是利用wordcloud.generate(text)函数或wordcloud.generate_from_frequencies(frequencies[,…])函数生成词云,前者是根据文本生成词云,后者是根据词频生成词云;三是利用wordcloud.to_file(file_name)函数将词云输出到文件进行保存。
(7)
设椭圆中心坐标为(x0,y0),长轴半径为ra,短轴半径为rb,椭圆偏角(椭圆短轴与水平方向的夹角)为θ,则计算椭圆如式(8)所示。
(8)
联立(5)和(8)可得[13]:
(9)
此时经投影变换二次曲线对应的矩阵形式分别为

2.2.3 椭圆筛选准则
通过最小二乘法对椭圆进行拟合,精确获取标靶特征圆。为了对拟合的候选“椭圆”进行筛选,以剔除由于环境光和其他因素造成的影响。具体通过以下3个准则来确定真实椭圆。
1)尺寸准则。通过判断提取出的轮廓内像素个数φ是否满足φmin<φ<φmax来确定并清除不在像素范围内的轮廓,φmin和φmax分别为最小和最大像素阈值。
2)圆度准则。设候选椭圆轮廓内点到椭圆的距离[14]为T,并设置一个误差阈值Terror,当l>Terror时,索引index+1,最后判断索引index的大小,如果index大于设置的阈值Tindex,认为此候选轮廓不是椭圆轮廓,则进行剔除。
3)长短轴比准则。当轮廓长轴大于3倍的短轴时,认为此轮廓倾斜角度过大,不符合椭圆轮廓特征,则进行剔除。

图5 同心椭圆效果图Fig.5 Concentric ellipse effect
2.3 编码标靶解码
由于拍摄角度的不同,环状标靶成像相较于实际三维图像会发生不同比例的收缩变换,对解码产生较大的影响,因此采用基于最小二乘法的仿射变换来矫正图像,使其成为正圆。仿射变换通过对图像进行旋转、平移,解决相机成像过程中的图像比例失调问题[15]。
对拍摄的图像进行仿射变换后得到圆环标靶,如图6所示。由图6可知,圆环M、N分别为编码带外环与内环,经过仿射变换可知,此时圆环M、N为标准圆,对两圆环之间的像素进行遍历,从而解得编码标靶。

图6 变换后的圆环标靶Fig.6 The transformed circular target
本文采用12位编码标靶进行编码,每一等分编码带所对应的角度为30°。通过使用Flann库中KD-Tree搜索半径最近点,得到每个角度对应半径范围内像素的数目l。l与设置的阈值T进行比较,如果l>T,则对应的二进制数字为1;否则,二进制数字为0。然后每隔30°进行一次搜索,得到一个12位的二进制数字序列b[i]。通过移位运算将此二进制序列b[i]转为对应最小十进制整数的二进制序列bmin[i],此时完成第一次遍历。第二次遍历相对于第一次遍历位置顺时针偏移1°,同样将得到的12位二进制序列转为对应的最小二进制序列。最后,将得到的30个对应最小二进制序列对应元素相加,并取平均值。分别对该序列的每一位数字进行判断,如果该数字大于0.5,则将该二进制数字设置为1;反之,则设置为0。此时得到的二进制序列即最终的二进制序列,将该序列转为十进制数,即此编码标靶对应的编码值,对应的标靶解码如图7所示。

图7 编码标靶解码图Fig.7 Decoding diagram of the coded target
3 试验与分析
本文采用分辨率为6 464像素×4 852像素的相机对同心圆投影变换的圆心提取方法的精度和环状编码标靶不同角度解码的精度进行验证。试验分为3部分:一是对同心圆中心提取精度进行测试分析,并与文献[3]中利用质心法所提取亚像素中心精度进行对比;二是对不同角度编码标靶解码的精度进行分析;三是对不同角度编码标靶重复性误差进行分析。
3.1 同心圆中心提取精度验证
将相机光轴与贴有编码标靶平面的夹角设置为60°,并对9个编码标靶进行圆心提取,以验证本文方法精度。圆心提取精度结果如图8所示。

图8 圆心提取精度验证Fig.8 Verification of circle extraction accuracy
图8(a)为本文圆心提取精度标靶图。图8(b)为采用编码值为1 365的12位编码标靶进行验证,以编码带内圈与外圈半径平均值画圆,得到图中红色轮廓,并与编码带相交于12个点。以图8(b)中Q为例,根据透视投影变换原理,理论上Q与Q′经过圆心,同理其余相交点两两之间连线也都经过圆心,通过最小二乘法求得距离6条直线最近的点为准确圆心。
将上述方法求得图8(a)中的全部圆心作为理想圆心,并与本文通过同心圆投影变换得到的圆心、非编码带外圆通过椭圆拟合得到的圆心、内圆通过椭圆拟合得到的圆心进行对比,结果如表1所示。
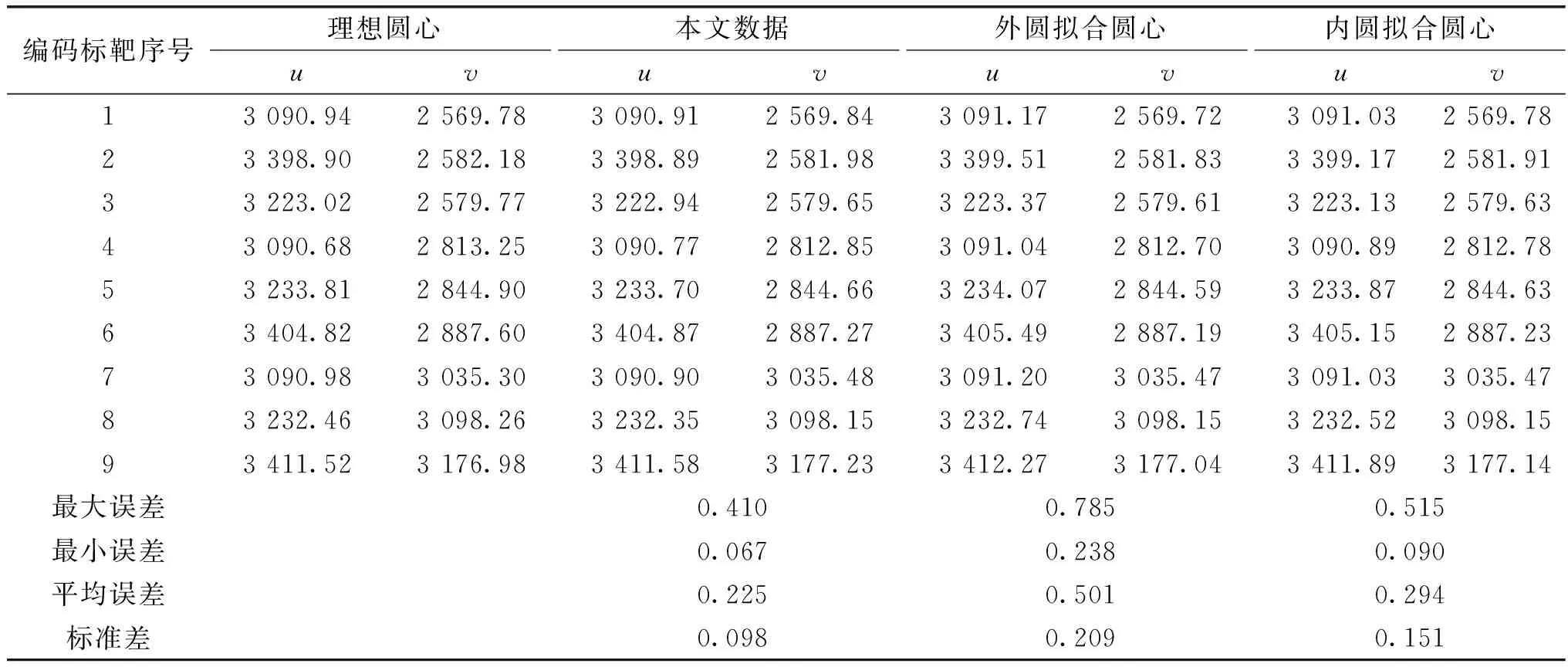
表1 不同方法所提取的圆心坐标对比 单位:像素
由表1数据可知,本文算法得到的中心圆与理想圆心的平均误差为0.225像素,相较于外圆拟合圆心平均误差(0.501像素)、内圆拟合误差(0.294像素)有所减少,这说明本文算法得到的圆心坐标更接近理想圆心,圆心定位精度更高。
为进一步验证本文提出的圆心提取方法精度,将本文算法提取到的编码标靶圆心与文献[3]中提出的方法进行对比。其中,文献[3]利用质心法对仿射变换后的单个编码标靶进行中心定位的方法,得到编码标靶的亚像素中心。分别采用理想圆心提取方法、本文同心圆提取圆心方法、文献[3]中的方法对图8(a)中的编码标靶进行圆心亚像素提取,结果如表2所示。

表2 与其他文献提取圆心坐标对比 单位:像素
由表2可知,本文所提出的方法在圆心提取平均误差和标准差方面都明显比文献[3]中利用质心法求得的圆心亚像素方法误差要小,更能适用复杂环境下对环状编码标靶的定位。
3.2 不同角度编码标靶解码验证
为验证本文解码算法的识别效果,采用不同角度对编码标靶识别率进行验证。本文选用的拍摄角度如图9所示,图9(a)~(e)分别为采用60°、65°、70°、75°、80°来进行验证。

图9 不同角度下编码标靶识别结果图Fig.9 The recognition results of coded targets under different angles
当相机光轴与编码标靶平面法线角度为75°(<80°)时,以图9(d)为例,提取标靶平面上64个编码标靶中心,提取标靶中心结果如表3所示。由表3得到的64个编码标靶中心坐标可知,在75°时标靶平面上所有编码标靶都能被提取出来,此时解码率为100%。当角度变为80°时,如图9(e)所示,只有46个编码标靶被提取出来,其解码率只有71.8%,因此建议在用编码标靶进行识别定位时尽量使得其角度在75°以内。
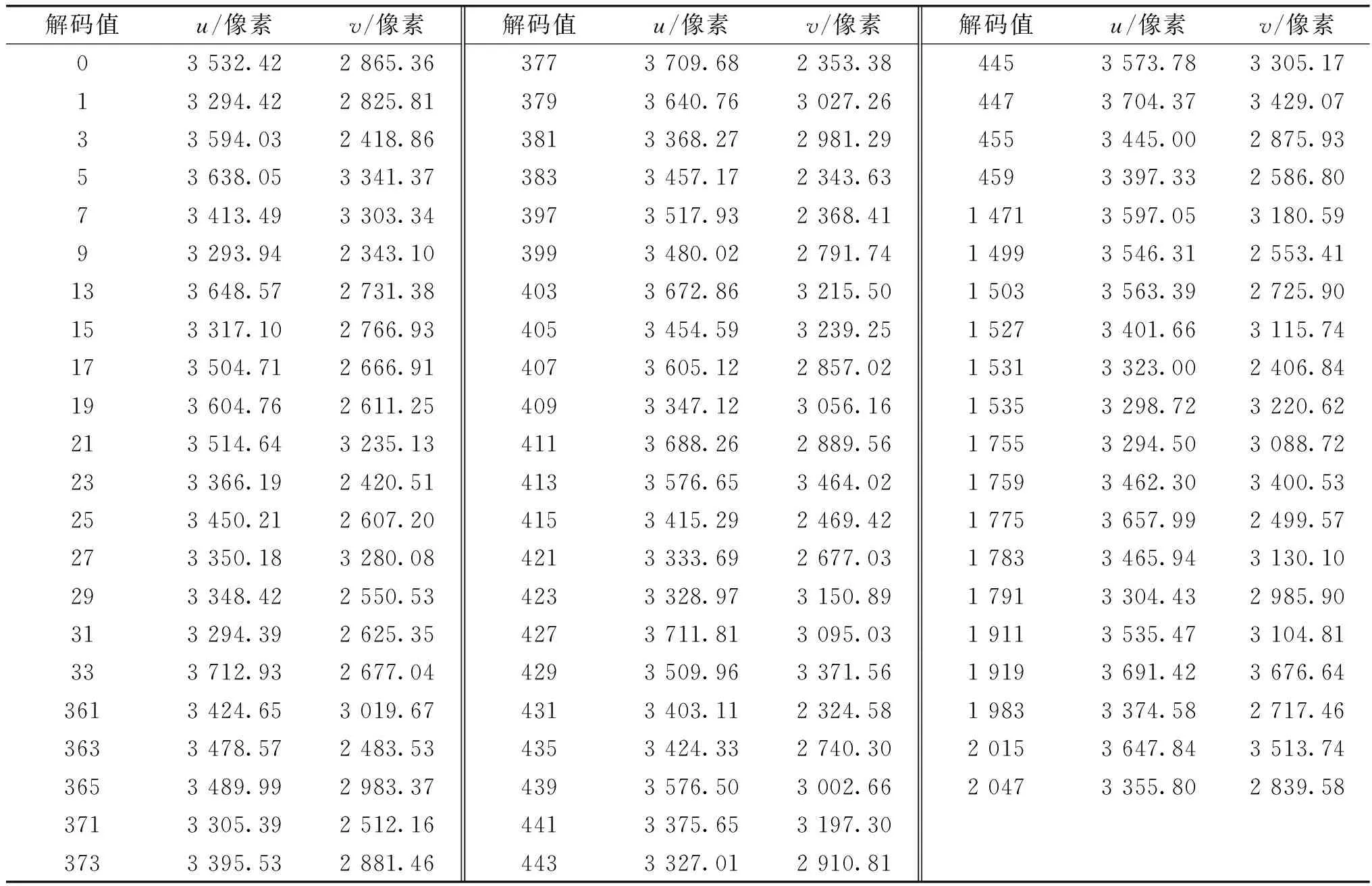
表3 相机与标靶平面呈75°时的编码标靶圆心提取Table 3 Coded target circle extraction when the camera is at 75° to the target plane
3.3 不同角度编码标靶重复性误差分析
将相机固定并调整标靶平面与相机的角度,相机曝光设置为40 000 μs条件下采用同心圆环提取编码标靶圆心的方式,分别对45°、50°、55°、60°、65°、70°、75°等7种拍摄位姿进行10次拍摄,最终得到圆心重复性误差最大值。不同角度提取结果如表4所示。

表4 不同角度提取圆心重复误差Table 4 Repetition error of circle center extraction at different angles
根据表4知,不同角度的编码标靶重复性误差均在0.1像素内,可以看出本文圆心提取方法能适应不同角度拍摄条件,且稳定性较高。
4 结 语
本文提出了一种基于同心圆投影变换求解圆心的方法。该方法利用同心圆投影变换后圆心唯一的特性,对投影变换后的两椭圆矩阵进行线性组合,从而确定同心圆圆心即为此线性组合矩阵第三个特征值所对应的特征向量。此外,对于编码标靶的识别,设计了一套基于最小二乘仿射变换方法的编码标靶编解码流程。
为验证本文的方法提取椭圆圆心的精度,在相机光轴与编码标靶平面法线成60°角度的情况下,利用最小二乘法求得编码值为1 365的编码标靶理想圆心。试验结果表明,所求得的圆心距理想圆心的平均误差为0.225像素,小于内外圆拟合的平均误差,更接近真实圆心。对于编码标靶的识别,采用相机与编码标靶夹角在75°以内有良好的解码效果。
本文提出的对编码标靶精确定位的方法能够适应复杂环境的要求,并很好地对圆心进行定位,进而提高摄像机的标定与特征点立体匹配精度。

