基于短时傅里叶光谱与数据融合的土壤成分含量预测

任慧东,鞠 薇,程志友,张梦思

(1.安徽大学 电子信息工程学院,安徽 合肥 230601;2.安徽大学 互联网学院,安徽 合肥 230601)

土壤肥力是土壤质量的体现,土壤养分、机械组成、酸碱度(potential of hydrogen,简称p H)是衡量土壤肥力的重要指标[1-2].传统的化学计量学方法成本高、过程烦琐,而近红外(near-infrared,简称NIR)光谱分析技术利用待测样品的光谱矩阵进行建模,具有快速、非破坏、无污染等优点,已广泛应用于农业、食品、药物、化工等领域[3-4].在农业生产领域,土壤养分、酸碱度的检测结果可指导施肥策略,提升作物产量和品质[5].

目前,国内外对土壤成分的光谱回归建模,具有光谱来源单一、样本少的特点.科研人员对数据量大、光谱来源多样的土壤光谱数据的研究较少.由于土壤成分复杂及土壤近红外光谱含有较多噪声,因此在土壤近红外光谱回归建模前需对光谱进行预处理.通过预处理的光谱建立回归模型,可获得更高的预测精度.传统的土壤光谱建模,主要使用偏最小二乘回归(partial least squares regression,简称PLSR)[6]、支持向量回归(support vector regression,简称SVR)[7]等机器学习方法.机器学习虽有速度快的优势,但其预测精度已被以卷积神经网络(convolutional neural network,简称CNN)为主的深度学习模型超越.文献[8]使用1维卷积神经网络预测了土壤pH、有机碳(organic carbon,简称OC)和钙含量,其平均误差相对于受限玻尔兹曼机更小.文献[9]使用CNN 从原始频谱中提取局部特征,通过循环神经网络学习特征序列的依赖关系,建立了基于CNN和循环神经网络的土壤光谱模型,该模型的决定系数均优于PLSR(partial least squares regression),SVR(support vector regression)等传统模型.文献[10]采用主成分分析将原始光谱降维,通过长短期记忆网络建立回归模型,对OC含量的预测明显优于PLSR模型.光谱神经网络建模主要使用1维光谱,有研究人员提出将光谱从1维数据转化为2维数据,以获得更丰富的特征.文献[11]利用短时傅里叶变换(short-time Fourier transform,简称STFT)将1维光谱数据转化为2维数据,据此构建了土壤成分的2维卷积神经网络模型,证明了时频分析在光谱建模中的有效性.文献[12]使用2维等高线图表征同步相关谱和异步相关谱,将1维光谱转化为2维相关光谱,突出了小峰和弱峰.文献[13]基于2维相关光谱技术提出了小米含水率的PLSR预测模型,相对于1维PLSR模型获得了更高的预测精度.考虑到不同成分对近红外光谱散射的影响,文献[14]在建模时使用多元回归预测多个成分含量,证实了不同土壤成分的吸收峰间有隐性关联.文献[15]将对NIR光谱和中红外光谱的数据进行融合,通过融合光谱构建CNN 模型,融合光谱的预测精度优于NIR光谱和中红外光谱的预测精度.文献[16]通过原始光谱及其预处理光谱构建集成学习模型,发现不同近红外预处理光谱间具有互补性.该文拟提出Inception 层短时傅里叶变换卷积神经网络(inception short-time Fourier transform convolutional neural network,简称I-STFT-CNN)单一光谱模型,然后提出2 个融合光谱模型II-STFT-CNN(indirect inception short-time Fourier transform convolutional neural network)和CI-STFT-CNN(cascade inception short-time Fourier transform convolutional neural network),最后对这些光谱模型的性能参数进行比较.

1 方 法

1.1 预处理和模型

1.1.1 光谱预处理

光谱仪测得的土壤近红外光谱易受土壤粒径及含水量等因素的影响,因此需对光谱进行如下预处理.

(1)标准正态变量(standard normal variational transform,简称SNV)变换.对每条土壤光谱进行标准化,以最小化因土壤粒径不均及颗粒表面散射等原因造成的光谱波动与偏移.波长i的SNV 变换预处理后的光谱反射率为

其中:Xi为波长i的原始光谱反射率，为波长i的原始光谱平均反射率,σ(Xi)为波长i的原始光谱反射率标准差.

(2)SG(Savitzky-Golag)平滑.SG平滑通过邻域平均增强光谱的平滑性,减少噪声的干扰.经SG平滑后的光谱反射率列向量为

其中:X为光谱反射率列向量;T为平滑矩阵,其表达式为

其中:(t-n)为波长序号,k为平滑多项式的阶数.

1.1.2 单一光谱模型

基于光谱前后波长特征峰的隐性关联特性,该文提出I-STFT-CNN单一光谱模型.

Inception层的结构如图1所示.将上层网络输出的特征Previous layer输入4个通道.通道1将输入此通道的特征与大小为1×1的卷积核做卷积,改变通道数;通道2将输入此通道的特征与大小为3×3的卷积核做卷积,提取输入特征中大小为3×3的区域特征;通道3将输入此通道的特征与大小为5×5的卷积核做卷积,提取输入特征中大小为5×5的区域特征;通道4首先将输入此通道的特征最大池化,其次将特征降维,最后将其与1×1的卷积核做卷积,改变通道数.4个通道输出的特征通过补零在尺度上保持一致,将这些特征在维度上进行合并后作为Inception层的输出.通过4个通道不同尺度特征的提取,Inception层输出的特征中包含了光谱不同空间尺度特征隐含的关联特征,有助于提高模型的精度.

图1 Inception层的结构

该文提出的单一光谱I-STFT-CNN模型结构如图2所示.近红外光谱经STFT(窗函数为Hann、窗长为100、重叠率为50%、采样频率为1)转化为大小为51×85的2维数据,将其作为模型输入.卷积层和全连接层均后接ReLu激活函数.经4层卷积层、1层Inception层提取特征后,使用Flatten将特征展平,然后经3层全连接层输出土壤成分含量的预测值.

图2 单一光谱I-STFT-CNN模型的结构

1.1.3 融合光谱模型

SNV变换对Raw光谱进行预处理后的光谱称为SNV光谱,SG平滑对Raw光谱进行预处理后的光谱称为SG光谱.该文分别通过扩展和级联对3种光谱(SNV,SG 及Raw 光谱)进行融合,提出2个融合光谱模型,分别记为II-STFT-CNN和CI-STFT-CNN,二者具体的模型结构如图3所示.II-STFTCNN先分别对3种光谱进行STFT变换得到3个大小为51×85的数据,再将其整合成大小为51×85×3的融合光谱.CI-STFT-CNN先将3种光谱级联,后对级联光谱进行STFT变换得到大小为51×253的融合光谱.

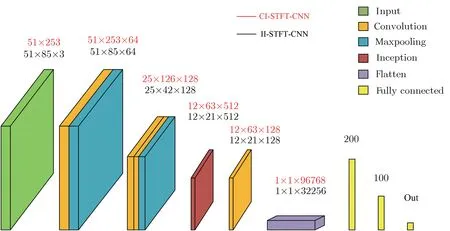
图3 融合光谱模型的结构

1.2 性能参数

决定系数表述模型的预测值与真实值的拟合程度,其计算公式为

均方根误差描述模型对极端值的拟合能力,其表达式为

RM越小,模型对极端值的拟合效果越好.

相对分析误差描述模型的检测能力,其表达式为

其中:S为预测值和真实值间的标准差.RP＜1.4时模型对数据的预测能力差,1.4＜RP＜2时模型对数据预测能力强,RP＞2时模型对数据的预测能力很强.

2 实 验

2.1 实验数据

该文使用的数据集为欧盟统计局2009—2011年采集的土壤利用及覆盖统计调查(land use/cover area frame statistical survey,简称LUCAS)数据集.LUCAS数据集包含欧盟27国共17 939条土壤光谱和成分参数数据.土壤样本分为矿物质和腐殖质两类,包括耕地、林地和草地等多种土壤类型.LUCAS土壤光谱是通过近红外光谱分析仪FOSS XDS测量得到的,该光谱仪的测量范围为400～2 500 nm,分辨率为0.5 nm.将数据集按7∶3的比例分为训练集和测试集,训练集和测试集的相关数据如表1所示.在训练卷积神经网络模型时将训练集以7∶3的比例分为校正集和验证集,校正集用于训练模型,验证集用于选择最优模型.

表1 训练集和测试集的相关数据

2.2 原始光谱与预处理光谱

随机从LUCAS数据集中抽取1条土壤近红外光谱,画出其SNV,Raw及SG光谱,如图4所示.从图4可看出:SG光谱和Raw 光谱几乎重合,SG 平滑仅消除了细微噪声,对光谱的整体走势无影响;SNV 光谱和Raw光谱二者存在较大差异,消除散射影响后,SNV光谱中450,1 400,1 900,2 250 nm 波长附近的波峰放大更明显.

图4 原始光谱和预处理光谱

2.3 不同单一光谱模型的性能参数对比

将单一光谱I-STFT-CNN 模型中的Inception层换为卷积层后的模型(其余参数不变),记为STFT-CNN,将其作为对比对象之一.训练神经网络模型使用的学习器为Adam,学习率为0.000 1,Batch size为32,Epoch为300.传统的单一光谱模型中使用最广泛的模型为PLSR和SVR.对4种单一光谱模型(SVR,PLSR,STFT-CNN,I-STFT-CNN)决定系数进行对比,结果如表2所示.

表2 4种单一光谱模型的决定系数对比

由表2可知,相对于SVR,PLSR和STFT-CNN 模型,该文提出的单一光谱I-STFT-CNN 模型的决定系数最高,表明I-STFT-CNN模型具有更高的预测精度.

2.4 单一光谱与融合光谱模型的性能参数对比

由上节可知,I-STFT-CNN 模型的土壤成分参数预测精度比SVR,PLSR 更高,故该节只需将ISTFT-CNN模型与两种融合光谱模型进行对比.表3为单一光谱I-STFT-CNN 模型与融合光谱IISTFT-CNN和CI-STFT-CNN模型的性能参数对比.

表3 单一光谱与融合光谱模型的性能参数对比

由表3可知,单一光谱I-STFT-CNN模型相对于两种融合光谱模型,其决定系数更小、均方根误差更大、相对分析误差更小,表明融合光谱模型的预测精度优于单一光谱模型,这是由于融合光谱数据具有更多特征;级联融合CI-STFT-CNN 模型与通道融合II-STFT-CNN 模型的有机碳含量的均方根误差相同,除此之外,级联融合CI-STFT-CNN 模型的各项性能参数均优于通道融合II-STFT-CNN 模型,表明级联融合效果优于通道融合,这是由于梯度反向传播时,级联光谱间的关联特征位于前级,更容易跳出局部最优解.

3 结束语

该文提出了单一光谱I-STFT-CNN 模型,以及2个融合光谱模型II-STFT-CNN 和CI-STFTCNN.对这些光谱模型的性能参数进行比较,结果表明:相对于SVR,PLSR和STFT-CNN 模型,该文提出的单一光谱I-STFT-CNN 模型具有更高的预测精度;融合光谱模型的性能优于单一光谱模型;融合模型中,级联融合CI-STFT-CNN 模型的性能优于通道融合II-STFT-CNN 模型.因此,该文提出的CI-STFT-CNN模型的预测精度最高.