基于多光子叠加态的交叉相位调制耦合参数测量

何天宇,林 志,李曦坤,杨 青,杨 名

(安徽大学 物理与光电工程学院,安徽 合肥 230601)

提高测量精度一直是量子计量学追求的目标,弱测量[1]的弱值放大效应为微小物理量的测量提供了途径.弱测量可用于光束横向偏转[2]、旋转色散效应的角旋转[3]、频率偏移[4]、Goos-Hänchen位移[5-6]以及光力学[7-9]测量.弱测量的放大效应需以降低概率为代价,针对弱测量的放大效应是否可以弥补减少的概率的这个问题,许多研究工作[10-13]给予了否定答案.但是,有一些研究人员[14-18]试图改善弱值放大的负面效应.文献[19]指出,后选择本身包含参数信息,利用这个信息有望达到量子计量学的海森堡极限,这为量子计量学提供了新的思路.利用纠缠态实现量子增强是量子计量学的主流方法.文献[17]利用纠缠态提高了弱测量的效率,在放大效果不变的前提下提高了后选择概率.纠缠态并非提高测量精度的唯一途径,有研究工作[20-24]表明,粒子之间的相互作用也是提高测量精度的重要资源.在探针与信号相互作用中,耦合参数信息被编码至探针,通过增加探针中的粒子数量m可实现测量精度的提高.不使用量子资源的测量精度为量级,利用m个纠缠粒子可将测量精度提高至1/m量级,通过k阶相互作用能得到1/mk量级的测量精度[20].文献[25]提出了一种测量交叉相位调制耦合参数的方案,利用单光子叠加态和相干态的耦合实现了精度为海森堡极限的测量.但是,对于交叉相位调制这种2阶非线性相互作用,海森堡极限并不是它的精度极限,故该文提出基于多光子叠加态的交叉相位调制耦合参数测量方案,探索提高测量精度.

1 交叉相位调制

图1为单光子叠加态的交叉相位调制(cross phase modulation)[25]耦合参数测量的示意图.图1中,上下两条红线分别表示信号光与探针光,信号光量子态为单光子的叠加态,探针光量子态为相干态|α>,两束光同时入射至非线性介质.红线水平向右的方向表示顺时序方向.信号光与探针光在非线性介质中发生相互作用(即交叉相位调制),其哈密顿量分别为信号光和探针光的粒子数算符,g为耦合常数,该过程对应图1中的蓝色区域.信号光的单光子叠加态与探针相干|α>态发生相互作用后,二者的联合态演化为

图1 单光子叠加态的交叉相位调制耦合参数测量的示意图

费舍信息包括量子费舍信息和经典费舍信息.耦合参数的测量精度可由Cramér-Rao边界Δg≥和Quantum Cramér-Rao边界描述,Δg为参数估计值gect与实际值greal的均方差,ν为重复测量的次数,F和Q分别为经典费舍信息和量子费舍信息[26-30].通过计算交叉相位调制中的联合态量子费舍信息Ij,可估计联合态中蕴含待测参数信息的多少,其表达式[19]为

其中:探针中相干态的平均光子数n=|α|2.信号光为单光子叠加态,如果探针为平均光子数很大的相干态,即n2≫1,则可认为参与本次测量的总光子数为相干态的平均光子数.从式(1)可知,联合态上进行的测量使耦合系数能达到.这个结果表明,只要选择合适的测量策略,就有可能使耦合系数的测量精度达到海森堡极限,所以接下来设计合适的投影测量,以实现海森堡精度.

信号光量子态与探针光量子态发生相互作用后,系统状态将获得一个相位,然后对信号光量子态进行投影测量,这一操作对应弱测量框架中的后选择.由于相互作用,投影测量使测量结果的概率随耦合系数发生变化,通过收集投影测量结果可获得参数信息;从另一个角度看,对信号光量子态进行投影测量会影响探针光量子态的波函数,因此对探针光量子态进行探测也可获得参数信息.

2 后选择策略

在弱测量框架下,耦合参数被编码至探针态波函数及后选择概率.联合态的量子费舍信息Ij分配于后选择保留的探针态量子费舍信息Qd、后选择舍弃的探针态量子费舍信息Qr以及从后选择概率中提取的经典费舍信息F.在此过程中,费舍信息有损失,该损失与后选择策略有关.各部分费舍信息的关系为Ij≥PdQd+PrQr+F[19],Pd为投影测量成功概率,失败概率Pr=1-Pd.通过选取合适的后选择策略,可使该费舍信息的损失降为零,使上述不等式取等号.由此可见,后选择无疑是弱测量框架下的重要环节,后选择策略对提取参数信息有重要影响.该文拟定两种投影测量策略(光子数态投影测量策略和光子数叠加态投影测量策略),对比这两种策略的费舍信息损失,并据此选取一个最佳策略.

2.1 光子数态投影测量策略

光子数态投影测量策略是将量子态投影到光子数态的测量策略.受信号光的光子数态投影测量的影响,探针光量子态变为由于量子力学投影测量必须保持完备性,则在投影过程会出现另一情况,此时探针光量子态为|ϕr>=|α>,其

通过Pd和Pr,可提取经典费舍信息,其表达式为

通过投影测量成功与失败时的探针光量子态,可分别提取Qd和Qr,Qd和Qr的表达式分别为

根据式(2)～(4),可得到投影测量后的各部分费舍信息的数值关系为PdQd+PrQr+F=2n.该策略下,因为2个部分费舍信息均为0,故只能从第3个部分费舍信息中获得参数信息.通过Ij≥PdQd+PrQr+F,可知该策略不能提取全部参数信息,即有信息损失.另一方面,该策略的费舍信息只出现了n的1次方项,故其测量精度没有达到海森堡极限.

2.2 光子数叠加态投影测量策略

光子数叠加态投影测量策略是将量子态投影到光子数叠加态的测量策略.将信号光量子态投影到光子数叠加态),投影测量成功和失败时的探针态分别演化为和|ϕr>=,投影测量成功和失败的概率表达式分别为

当耦合参数的数值非常小(g→0)时,式(5)～(6)可近似为

其中:n为相干态平均光子数.光子数叠加态投影测量策略下的各部分费舍信息为

与光子数态投影测量策略不同,光子数叠加态投影测量策略的成功概率几乎为0,而失败的概率几乎为1(这个结论可从式(7)～(8)得出).然而,尽管概率很低,但由式(10)可知费舍信息Qd数值很大.综合考虑概率与量子费舍信息数值,将探针量子费舍信息乘以对应的投影概率,得到

与光子数态投影测量策略不同,光子数叠加态投影测量策略中没有发现费舍信息为0的情况,各部分的费舍信息的关系为Ij=PdQd+PrQr+F.除此之外,光子数叠加态投影测量策略的经典费舍信息出现了n的2次方项,故光子数态叠加态投影策略可使测量精度达到海森堡极限.

3 信号光量子态筛选

下面对信号光的量子态进行筛选,以获取更高测量精度.相对于单光子的叠加态,多光子叠加态在希尔伯特空间有更多维度.多光子叠加态具有多种形式,在此考虑以下3种形式:和|N>.这3种量子态信号光与探针光相互作用时,其联合态分别演化为

其中:联合态的上标0N,012N,N分别对应的信号光量子态为|2>+…+|N>),|N>.

计算可得3种联合态的量子费舍信息分别为

式(17)～(19)中均出现了N的2次方,这表明多光子叠加态可带来增强效应.但不同的量子态之间依旧存在差异,式(19)中出现了N的2次方,而n只有1次方,这是因为信号光量子态没有叠加资源.将式(17)与式(18)进行对比,可以看出多维叠加态在N较小时可带来增强效应,而在N较大时其增强效应会弱于2维叠加态的增强效应.这种情况的出现,可能与大N下多维叠加态中的最大光子数态的叠加系数显著减小有关.

由于联合态的量子费舍信息数值比其他两种量子态的量子费舍信息数值高,故该文选择信号光的量子态为),通过后选择策略,能使基于多光子叠加态的测量精度比基于其他两种量子态的测量精度更高.

4 基于多光子叠加态的交叉相位调制耦合参数测量方案

该文提出基于多光子叠加态的交叉相位调制耦合参数测量方案.投影至光子数叠加态而非光子数本征态,才能避免参数信息丢失.从弱值放大角度看,需要将信号光量子态投影至几乎正交的量子态,这样可获得更大的弱值,以提升测量精度.因此,将后选择态取为,其投影概率为

当耦合参数的数值非常小(g→0)时,式(20)可近似为

测量后探针光量子态塌缩为

由于投影测量须保持完备性,故投影测量也可出现另一种结果,此时探针光量子态塌缩为

根据式(22)～(23),可得

因此,多光子叠加态方案测量精度是单光子叠加态方案测量精度的1/N2,且多光子叠加态方案各部分费舍信息数值分别是单光子叠加态方案对应的各部分费舍信息数值的N2.当耦合参数g的数值非常小(g→0)时,信号光为单光子叠加态及多光子叠加态的测量概率分别近似为,表明多光子叠加态方案测量概率是单光子叠加态方案测量概率的N2倍.因此,多光子叠加态的信号光能使测量结果得到全方位提升.

图2为该文提出的基于多光子叠加态的交叉相位调制耦合参数测量的物理方案意图.

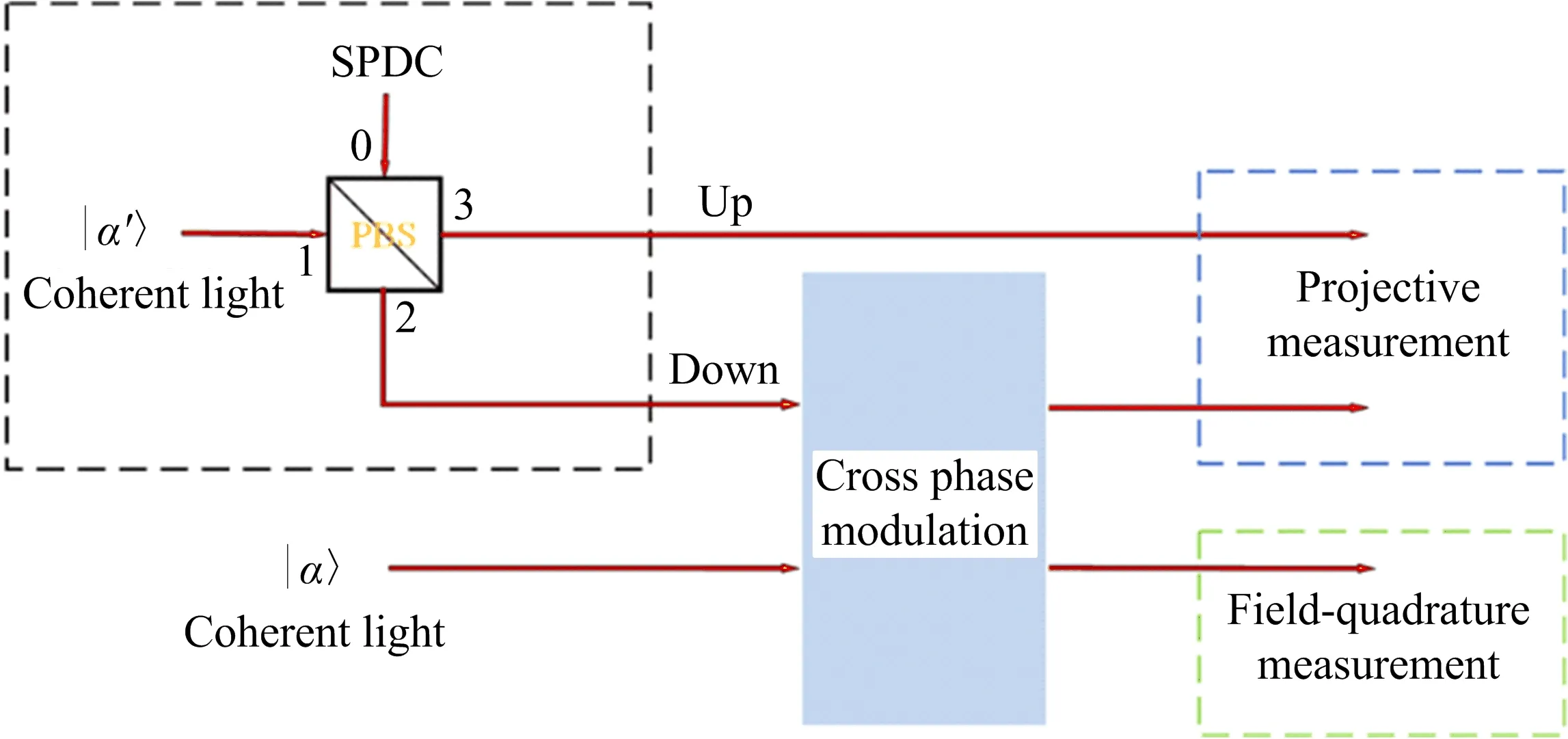
图2 基于多光子叠加态的交叉相位调制耦合参数测量的物理方案示意图

图2 中,黑色虚线区域对应多光子叠加态的制备过程[31-32],在偏振分束器(polarizing beam splitter,简称PBS)的两个输入端(0,1端)分别输入自发参数下转换(spontaneous parametric downconversion,简称SPDC)光和相干光,这两束光经过PBS并发生干涉.两个输出端(2,3端)的几乎全部光子均从共同的输出端(2端或3端)离开PBS并进入同一条路径(Up路径或Down路径).使用一个50/50的PBS,就能得到全部光子等概率进入Up路径或Down路径的结果.当光子全部进入Down路径时,与探针光发生交叉相位调制(对应图2中蓝色区域),而进入Up路径的光子则不与探针光发生交叉相位调制作用.可见,该物理方案具有搭建难度低及操作简单的优点.

对信号光量子态进行投影测量,待测参数信息将编码于测量后的探针光量子态及对应的概率.投影测量的结果影响探针光的波函数.通过对探针光量子态进行正交测量能估测参数,并获得与其量子费舍信息量级对应的测量精度.

5 结束语

该文在弱测量的框架下,基于单光子态信号光与相干态探针光交叉相位调制的相互作用,讨论了两种不同投影测量策略对提取参数信息的影响.两种策略结果的对比表明:投影至光子数叠加态的测量为最佳投影测量,而投影至光子数本征态的测量会带来参数信息丢失.该文将单光子态与相干态交叉相位调制的讨论拓展至多光子情况,讨论了3种不同叠加形式的信号光量子态对费舍信息的影响,从3种不同量子态中选择最佳量子态.相对于单光子叠加态的方案,多光子叠加态方案的测量效果有全方位提升.最后,提出了基于多光子叠加态的交叉相位调制耦合参数测量的物理方案.有关交叉相位调制耦合系数测量精度仍有提升空间,后续研究可利用其他量子资源获取更好的测量精度,例如用纠缠态提升测量精度.