基于多曲率融合的铣刀缺陷检测*

易 忠,周 骅,赵 麒,袁学枫

(1.贵州大学大数据与信息工程学院,贵阳 550025;2.贵州民族大学机械电子工程学院,贵阳 550025)

0 引言

铣刀作为机械加工中的重要铣削工具,是机械产品的加工基础,也是各种一体成形产品的主要工具,在机械加工、制造中具有重要地位,对铣刀质量的检测显得尤为重要。目前,在专业的铣刀数控加工生产中心,对生产出的铣刀质量检测,通常是工业相机加显微镜头的组合,将样本画面放大以后通过人工来判断样本是否合格,因为人眼的易疲劳性,这种检测方法成本高且效率低。谢峰等[1]采用自适应随机共振算法来检测立铣刀的磨损状态,通过采集转动的相关参数来判断铣刀是否合格,但该种方法并不能定位缺陷类型和位置,且对设备要求较高;李宇庭等[2]通过建立特征数据集、使用遗传算法和SVM模型实现了对腐蚀坑和裂纹两种缺陷的高精度分类算法;刘浩[3]使用图像差分算法和SVM分类算法对刀尖表面缺陷进行检测和分类。计算机视觉作为当前缺陷检测的主流,具有成熟的应用范围,常见的深度学习算法需要足够的训练样本和高性能的运算单元,且存在许多的浮点运算,在工业应用的嵌入式平台中普适性较差,且目前在公开的网络资源中,并没有铣刀的缺陷样本集,很难有好的训练模型。传统图像差分和模板匹配算法对模板和样本的相似性进行评分,为了解决图像采集时因缩放、旋转等导致的目标分辨率和角度不一致的问题,大多采用特征匹配的方法,需要对不同样本设计相应的特征评价体系,且对缺陷处进行定位较为困难。

针对以上问题,本文提出一种基于改进链码计算机制的铣刀缺陷检测方法,在对样本图像处理得到铣刀边缘轮廓后,使用该方法对铣刀轮廓坐标进行曲度计算,通过对曲度峰值点的判断和筛选定位到铣刀崩刃、多刃缺陷处位置。经实验验证,该方法提高了检测速度和精度,更贴合嵌入式平台的使用。

1 铣刀崩刃检测原理

常见的铣刀样本,为外刀刃弯曲加上内刀刃直线组成的四刀刃,相较于常见的直线型铣刀,图像差分方法和直线拟合方法难以适用,因此提出以下的检测方案:

(1)使用自主选型的相机、镜头和光源组成的实验平台进行样本图片采集。

(2)对样本图片进行背景分离,得到铣刀主体。

(3)使用双边滤波平滑样本内部和强化边缘,并进行铣刀轮廓提取。

(4)使用改进的链码计算机制对轮廓像素点坐标进行曲度计算。

(5)筛选曲度峰值点,去除标准点,得到铣刀崩刃、多刃缺陷的位置(若样本合格则不存在缺陷点)。

1.1 铣刀背景的分离

如图1所示,图片背景区域杂色为相机所在环境反光所致,这部分对计算时会造成干扰,因此将前后背景分离,铣刀刀身颜色和背景色呈现明显差异,且工业相机所在位置基本固定,所以采用RGB通道色彩抑制去除背景色,在拍摄环境和拍摄位置不变化情况下,对图1所示的样本环境,设置阈值分别为:R>97,G>59,B>91。

(a) 原图 (b) 前景图

在色彩分离过程中,刀身本身会受到色彩的略微影响,剔除小于阈值的色彩值后会有失真的情况出现,选择增加光照强度解决此问题,将RGB色彩影响降低,争对现有的实验条件,该方法能直接应用于背景杂色的环境,更换更高规格的相机和高质量镜头后,此方法也可以用来降噪。

1.2 铣刀样本的去噪

铣刀刀刃是图1a中单边外围轮廓部分,为了提取刀刃的准确轮廓,降低拍摄成像时噪声的干扰,需要对图片进行滤波处理,常用的滤波算法有中值滤波、均值滤波、双边滤波等,铣刀需要得到清晰的边缘,所以需要将刀刃锐化,将非边缘处平滑,采用双边滤波算法,并将小的连通域当作干扰删除。双边滤波可以减少图像中的锯齿和亮度动态范围不平衡带来的影响。

设定滤波半径为5,全局方差为5,局部方差为0.2,滤波结果如下,图2大小为1600*1200,设置小连通干扰区域面积阈值为10 000。

(a) 原图 (b) 双边滤波图 (c) 去小区域图

(a) 刀刃二值图 (b) 刀刃轮廓图

1.3 铣刀轮廓提取

将图像二值化,不仅可以降低计算量,也更方便对边缘进行处理,将连通域标记以后,使用下述流程提取边缘并储存边缘点顺序和坐标:

(1)使用LOG算子提取二值图的边缘,LOG算子在二值图像中具有良好的边缘提取效果,可以将边缘提取为单个像素宽度。

(2)将边缘轮廓内值的索引存放在矩阵中,m为行坐标索引,n为列坐标索引。

(3)将阵列中第一个点作为初始点,顺时针判断下一个点的位置并计算欧式距离是否等于1,如果距离为1,将该点标记为下一个点,将索引存入新的矩阵,单个连通域标记完毕,继续标记下一个连通域,直到将所有连通域标记完毕。

1.4 基于K邻域链码的拐点检测

在图像中,K邻域链码是指以某点为中心,从该点往右第K/8(K=8n,n=1,2,3…)点处赋值为0,再逆时针方向旋转依次赋值1,2,3…K-1形成的矩阵。

铣刀的崩刃、多刃处在二值轮廓中会形成一个或多个拐点,尚振宏等[4]提出一种在二值图像中拐点的实时检测算法(以下统称该算法为SH算法):通过对像素点处的曲率进行计算比较,得到图像中的拐点,其中Pi点处的曲率可由式(1)～式(4)得出,c(k,i)表示点Pi的链码值,标记与未标记表示同一个点是否被使用两次,当同一个点第二次被轮廓计入时则此点为标记点,该点是拐点的可能性更大。

(1)

(2)

(3)

如果像素P(i+k/8)不位于Pi的K邻域内,但位于Pi的k-8m邻域内(m=1,2,3,…,且k-8m≥8)。

c(k,i+k/8)≈c(k-8m,i+k/8)×[k/(k-8m)]

(4)

得到轮廓内所有点的曲率以后,将大于设置阈值的峰值点作为拐点。

在铣刀轮廓中,因为像素值的连续性,以及拍摄精度和角度导致的差异性,在刀刃尖端的位置,可能并不是由一个像素点构成,也就是说,铣刀刀刃尖端处存在多个像素点,在人眼观察到尖锐处,将其像素化后反而是多个像素点构成的扁平,将其变化到二维坐标系后差异更明显,如图4所示。

(a) 刀刃像素边界1(b) 刀刃像素边界2

显然,此时再将第一个拐点作为尖端点是不符合人的逻辑认知规律的,因此提出一种多点单邻域检测算法以及一种多点多邻域检测算法,用来高精度的检测铣刀刀口崩刃。

图5 重构链码中心

图6 图像采集平台

1.5 基于链码的多点单邻域拐点检测算法

SH算法是将P(i+k/8)处的位置由Pi处的链码表示而出,而Pi处的位置又由P(i-k/8)处的链码表示,因此实际上是Pi点与左右第K/8个像素点构成的两线段所组成的角度来作为曲度,对于规则的像素级曲线拐点,该方法具有良好的效果,但是在铣刀刀刃中,刀尖处并不是单像素点作为尖点,在崩刃和尖端处可能存在多个并排像素点,因此在此基础上提出了一种基于链码的多点单邻域算法,将K邻域链码的中心重构,并融合多点链码计算曲率值以增强抗噪能力和检测准确率。具体计算步骤为:

步骤1:对像素点Pi进行计算时,将其直接作为链码矩阵的中心。

步骤2:分别计算链码中心Pi处左边和右边第1至k/8个点相对于Pi的角点值(两链码差值的绝对值),不在链码k邻域内但在k-8m邻域内的点,仍使用倍率关系求取链码值。

(5)

(6)

步骤3:将Pi左右对应的角点值相减并取绝对值。

ce(n)=|θi+n-θi-n|

(7)

步骤4:若所得ce值为0,或大于k/2,则该值等于k减去本身。

(8)

步骤5:将得到的所有值求和。

(9)

步骤6:将得到的值使用最大值做差值并平方。两线段构成的角度越小,得到的c值越小,反之越大,数据平方化可以拉高曲点与平滑点的差距,更好的去除噪点干扰。

e(i)=(Max(c(i))-c(i))2

(10)

步骤4是因为以Pi为中心时,无论左右采用多少个点进行计算,两个点的链码值之差越小则证明三点构成的两线段角度越小,差值为0则为直线。使用中心左右第K/8个点进行计算,相比于使用多个点,使用两点的抗干扰性和准确性都比较低。

综上所述，动物防疫不仅是技术工作，也是行政工作，工作量频繁，涉及种类多，这也需要我们应改革和创新动物防疫管理制度，尤其是重大动物疫病防控免疫措施，更需要加强注重政府管理，创新运行制度，优化防疫执法，保证让免疫工作落实，让畜禽业能够健康稳定发展。

1.6 基于链码的多点多邻域拐点检测算法

在多点单邻域算法中,对点Pi左右的点进行角点值计算时,使用的都是同一个链码矩阵,对于大的拐点有较好的效果,为了检测相对平滑处的小拐点,提出一种多点多邻域算法,将多点单邻域算法中的步骤2做出修改:

(11)

(12)

1.7 基于多曲率融合的铣刀崩刃定位

通过图像的预处理分离背景,使用双边滤波和LOG算子提取到铣刀的边缘,再使用基于链码的多点单邻域算法提取到铣刀轮廓上的拐点以后,刀具轮廓上的所有拐点都已经被检测出,再次使用同样的处理方法对合格的刀具样本进行处理,得到刀刃上本身存在的合格拐点,将缺陷样本拐点与合格拐点做差分,剩下的就是铣刀的崩刃和多刃缺陷处。

2 实验分析

2.1 实验平台

实验平台PC环境为Intel(R) Core(TM) i5-3470 CPU,16 G运行内存,window10操作系统,基于MATLAB R2018软件平台计算;200 W像素迈德威视MV-GED200C-T-CLccd相机,海约HAYAER300倍光学显微镜头,华康科技HK-DLR-84-35型号穹顶光源、多用金属支架。

2.2 不同算法拐点定位

对同一段刀刃曲线使用3种算法计算,结果如图7所示,矩形框标记点为检测到的拐点位置;在曲线规则度差,拐点复杂的情况下,SH算法受干扰较大,相同拐点容易被错检,两种多曲率融合的检测算法检测更精准。

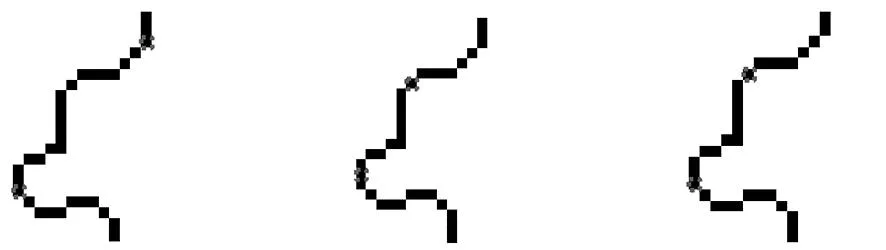
(a) SH算法检测 (b) 多点多邻域算法检测 (c) 多点单邻域算法检测

2.3 铣刀样本崩刃检测

对于像素点Pi处的曲度,由左右第1到k/8个点共同构成,更贴合铣刀刀刃的实际像素点构成的曲线,图8是同一样本不同邻域下使用多点单邻域算法计算到的曲率。

(a) 原图 (b) 轮廓图

使用3种算法分别计算单刃铣刀样本(分辨率803*659),阈值设置为刚好能检测到缺陷点又排除光滑合格点,参数为K=64,曲率阈值分别为:200、200、550;图9c～图9e为3种算法计算到图9b的曲率,图9f～图9h中边缘标记点为检测到的拐点,图9i～图9k中边缘黑色点为检测到的崩刃处;多点单邻域算法对单刀刃铣刀比多点多邻域算法多检测出了一处崩刃点,两种融合多曲率的算法比SH算法多检测到一处崩刃,而该处崩刃处所在轮廓曲线处较为光滑,证明融合多曲率的算法有更好的检测能力。

(a) 原图 (b) 刀刃轮廓图

计算样本2(分辨率1600*1200)结果为:图10c～图10e为3种算法计算到图10b的曲率图10f～图10h中边缘标记点为检测到的拐点,图10i～图10k中边缘白色标记点为检测到的崩刃处;因样本2有3个闭合区域,其曲率图为3区域并列,K=128,拐点阈值分别设置为:280、200、850。多点多邻域算法对平滑处的检测更敏感,而SH算法容易出现漏检的现象,多点单邻域算法不仅考虑了邻域内多点的值,也只使用最大的链码矩阵,不仅有较高的检测精度,也具有较强的抗噪能力。

(a) 原图 (b) 刀刃轮廓图

2.4 性能分析

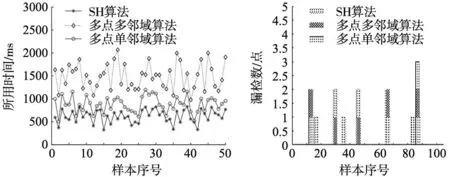
(a) 检测速度 (b) 漏检数目

SH算法检测速度略快于多点单邻域算法,但检测精度比后者更低,漏检率也最高,多点多邻域算法因为使用多个链码矩阵值,在速度上较之SH和多点单邻域算法都要慢。本批次100个样本中,SH算法检测准确率86%,平均检测时间621.06 ms;多点多邻域算法检测准确率为92%,平均检测时间1 480.54 ms;多点单邻域算法检测准确率为97%,平均检测时间748.71 ms。

经过实验分析,在同一个样本的检测中,SH算法存在漏检现象,对于形状对称的铣刀,SH算法只检测出了部分拐点,两对称点的曲率理论相同,但受到成像质量和边缘提取效果的影响,对称点的曲率可能存在略微差异,而SH算法只采用两点来计算曲度,容易受到噪声点的干扰,多点多邻域算法对噪声的包容性比SH算法更高,但在略微平滑处也存在多检、漏检现象,单邻域链码算法在整个铣刀刀刃曲线中有很好的检测效果,能将封闭轮廓中的各拐点都检测出来,同时也对光滑处的曲线不做标记,具有更高的抗噪能力和检测精度,在时间和检测质量上综合优于其他两种算法。

3 结论

实验证明,相比于传统的铣刀缺陷检测方法,本文提出的多点单邻域链码算法对铣刀的崩刃、多刃缺陷具有良好的检测效果,能判断铣刀是否存在缺陷并在有缺陷时准确定位到铣刀的崩刃、多刃缺陷处。该检测方法具有以下优点:

(1)速度快,基于多曲率融合的铣刀缺陷检测算法对四刀刃铣刀样本的平均检测时间在0.8 s,能满足工业在线检测的要求。

(2)精度高,通过实验验证,对任意刀刃的铣刀,只要存在崩刃、毛刺缺陷,检测结果精准,在崩刃或多刃大小相差较大时候,仍然有92%的准确率。

(3)包容性强,算法直接对像素坐标数据进行计算,不需要额外样本,对任意形状的铣刀都可以进行检测,不受样本采集时候角度、缩放等因素的影响。

(4)抗噪能力强,算法对样本进行滤波、小连通域去除等操作,噪声对检测结果的影响可以忽略不记。

(5)设备要求低,本算法不涉及大量运算,对平台的算力要求较低,更贴合嵌入式计算环境,可以将其应用到工业检测的一体化产品中,具有良好的使用前景和发展优势。