基于改进PSO算法的移动机器人最优路径规划*
党博宇,李海燕
(东北大学a.信息科学与工程学院;b.计算机科学与工程学院,沈阳 110819)
0 引言
路径规划作为机器人自主导航的核心技术,提出了多种算法,如A*算法[1]、蚁群优化算法[2]、改进人工势场法[3]、遗传算法[4]等。上述方法在环境简单、静态障碍物条件下,通过环境建模或者搜索可以完成路径规划任务[5-6]。然而,机器人实际运动中不仅有静态障碍物还有动态障碍物,现实环境通常具有不确定性,随机障碍物环境下机器人规划安全无碰撞的最优路径极为重要。
近年来,粒子群算法(PSO)由于搜索快速、效率高、算法易于实现,广泛应用于机器人路径规划的研究[7]。TANG等[8]提出了多机器人协同粒子群优化算法,改进了粒子停滞更新问题;ZHANG等[9]利用惯性权重和加速因子提高PSO算法的收敛速度,避免粒子陷入局部极小点;TAN等[10]将蚁群算法和PSO算法相结合,规划了点焊机器人的最优运动路径。上述研究仅考虑了运动环境中的静态障碍物,未能解决机器人遇到随机障碍物的问题。
移动机器人在实际工作场景中,由于运动环境的不确定性,往往会出现随机障碍物,严重影响机器人的安全运动。LI等[11]提出了A*和动态窗口(DWA)融合的轨迹规划算法,利用改进的A*算法规划全局路径,再结合DWA算法实现实时避障;KOBAYASHI等[12]提出了DWA方法,对静态和动态障碍物的位置进行预测,实现了虚拟机械手的路径规划;DAI等[13]提出了改进的Informed-RRT*算法并融合DWA方法,实现了机器人的自主导航。虽然上述研究利用DWA方法实现了动态障碍物的避障,然而没有考虑避开障碍物后再次返回已经规划的全局路径的问题,增加了重新规划路径的计算成本。
针对随机障碍物环境下移动机器人路径规划问题,本文利用随机数和权函数改进了PSO优化算法,构建了机器人的全局最优运动路径;再结合DWA方法安全避障全局路径上的随机障碍物,并确保机器人返回全局路径;通过仿真和实验研究,验证了文中方法的有效性和优越性。
1 移动机器人运动学模型
移动机器人结构如图1所示,其具有独立驱动的4个防滑车轮,每个轮子均由轮毂无刷电机、变速箱和编码器组成,可以快速适应复杂的运动环境,并实现自主移动。

图1 移动机器人结构
机器人运动学模型描述为:
(1)
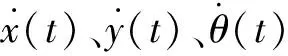

vmin≤v≤vmax
(2)
(3)
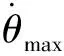
2 改进粒子群算法的最优路径规划
2.1 机器人的次优路径规划
为了构建机器人的可运动空间,利用MAKLINK线得到机器人的所有可允许运动路径(如图2所示),在此基础上采用Dijkstra算法规划机器人运动的次优路径。
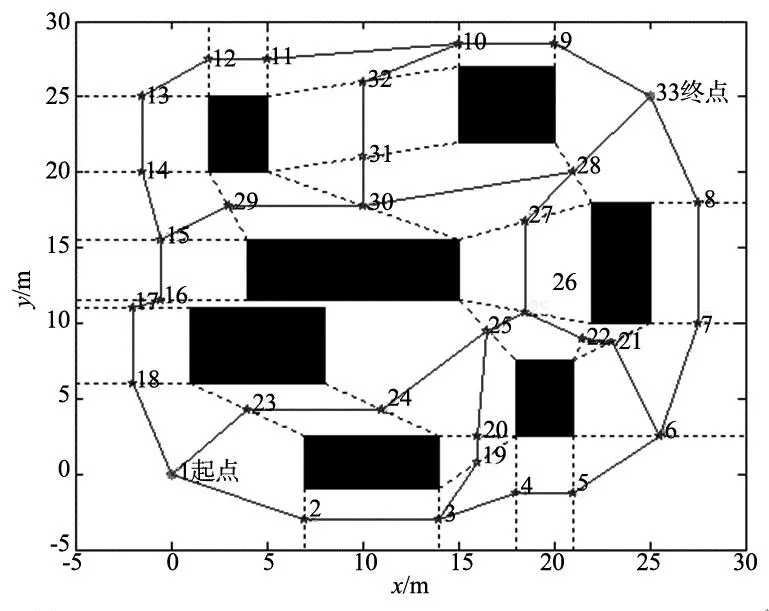
图2 机器人的运动路径
令d表示两连接点间的距离,从起点S1开始,有:
d(S1,Sj)=d1j
(4)
式中:Sj表示一个连接点,d1j表示距离值,j=1,2,3,…,n,d(S1,S1)=0。将所有连接点放在两个集合M={S1}和N={S2,…,Sn}中,并从N中逐一找到点Sk(k=2,3,…,n),使其满足:
d(S1,Sk)=min{d(S1,Sj)}
(5)
将式(5)搜索得到的Sk放入M中,并更新d(S1,Sj),直至搜索到目标点。于是有:
d(S1,Sk)=min{d(S1,Sj),d(S1,Sk)+dkj}
(6)
利用式(6)反复搜索得到的次优运动路径如图3所示。
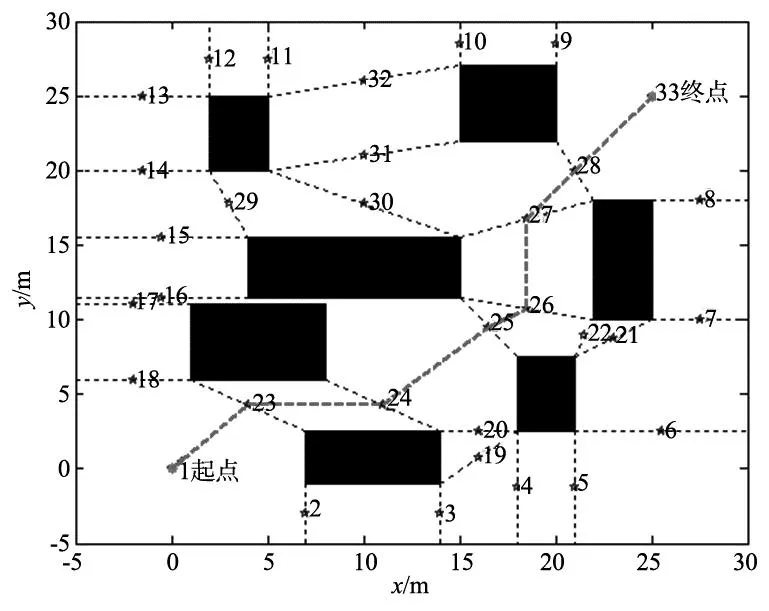
图3 机器人运动的次优路径
2.2 机器人的最优路径规划
为了得到移动机器人从起点到终点的最短运动路径,在获得次优路径图3的基础上,设计优化性能函数为:
(7)
式中:dl(l=1,2,3,…,7)表示图3中相邻的两个节点间的距离。
在PSO路径规划中,对于次优路径的链接线Pi1Pi2(i=1,2,3,…,6),每个粒子的位置xsi(s=1,2,3,…,m)用[0,1]间的比例数表示。因此,粒子的坐标(xPi,yPi)表示为:
(8)
这样利用式(7)和式(8)便可得到移动机器人的最短运动路径。
(9)
(10)
式中:t0表示每个粒子达到最优停滞的步数,tg表示全部粒子达到最优停滞的步数,T0和Tg分别表示个体最优和全局最优的阈值。
为了平衡全局和局部的搜索次数,构造权函数w为:
(11)
式中:a表示迭代次数,b表示最大的迭代次数。
利用式(9)~式(11)改进传统粒子群算法中粒子搜索的速度和位置,得到:
(12)
xsi(t+1)=xsi(t)+vsi(t+1)
(13)
式中:vsi(t)和xsi(t)分别表示粒子的速度和位置,r3、r4表示[0,1]上的随机数,c1、c2表示加速因子,gs(t)表示粒子个体的位置最优值,gg(t)表示粒子全局的位置最优值。
为了降低区间端点对粒子运动的影响,在迭代中对粒子的运动范围改进为:
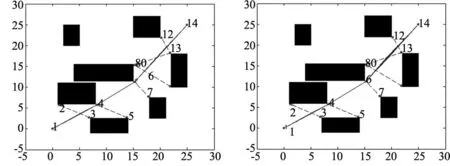
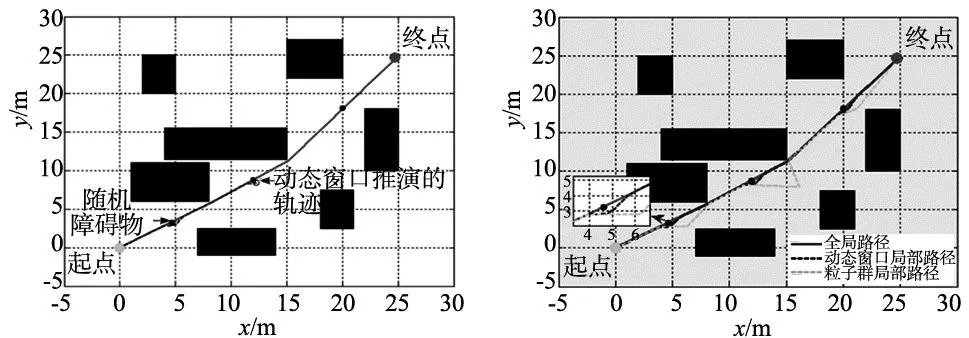
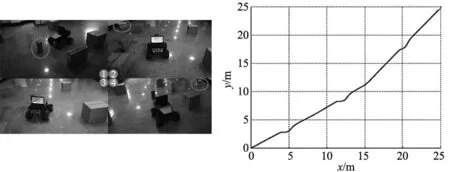
若xsi(t+1) 低年级孩子的书面语言学习刚刚起步,识字量、词汇量少,书面语言图式有限,写话时必然捉襟见肘,即使是初步理解和积累的部分,要达到能运用的水平,也还要有一个过程。所以要实现从随意的口头表达到有序的书面表达,是不小的一道坎。因而,教师需要选择贴近学生生活的文本进行模仿练笔,并且教师要善于将文本掰开了、揉碎了,让学生感受到文本的“有序”。以下是笔者在教学《我叫黑脸琵鹭》的仿写时,帮助学生建立有序表达的片段。 xsi(t+1)=Xmin+rand*0.01 (14) 若xsi(t+1)>Xmax,则: xsi(t+1)=Xmax+rand*0.01 (15) 式中:Xmin和Xmax分别表示粒子s运动位置区间端点的最小值和最大值。 这样利用上述改进的粒子群算法,移动机器人从起点到终点规划了最优的运动路径。 为了使机器人躲避最优路径上的随机障碍物,并回到已经规划的运动路径向目标点移动,文中提出了动态窗口随机避障方法,算法具体过程为: (16) (17) 步骤3:利用步骤2获得的安全运动速度,计算机器人一段时间的可行运动轨迹集,并对每条轨迹进行评价,评价函数为: (18) 这样机器人利用体感摄像头感知周围的障碍物信息,采用动态窗口方法,通过航迹推算和评价函数可以实现全局路径上随机障碍物的安全避障。 为了验证文中提出的改进粒子群方法和随机障碍物避障方法的有效性,与传统粒子群方法进行了仿真对比。仿真中粒子数n=40,迭代次数i=300,并且运行30次。改进粒子群方法和传统粒子群方法的路径规划结果分别如图4和图5所示。 图4 改进PSO算法规划的路径 为了进一步说明改进粒子群方法规划路径的优越性,与传统PSO各指标对比数据如表1所示。 表1 仿真结果对比 由表1可知,成功迭代次数相同的情况下,改进后的PSO算法相比于传统PSO算法,运行时间减少,粒子的位置和速度不断进行更新,得到了更短的最优运动路径。 为了进一步说明机器人避开随机障碍物并返回全局路径的动态窗口方法的有效性,与粒子群局部避障方法进行了仿真对比,结果如图6和图7所示。 图6 机器人躲避障碍物(本文方法) 图6给出了机器人在全局路径上躲避随机障碍物的仿真结果,可以看出动态窗口方法有效进行了局部路径规划,保证机器人避开随机障碍物后返回全局路径。图7给出了动态窗口方法和粒子群方法局部路径规划的仿真对比结果,由图可知,动态窗口方法可以规划更短更光滑的局部路径,最终到达目标点,而粒子群局部路径规划方法虽然躲避了随机障碍物,但躲避障碍物后不能及时返回规划好的全局最优路径,不仅增加了计算成本,而且比动态窗口方法避障的运动路径更长。 为了进一步验证文中提出的随机障碍物环境下最优路径规划方法的有效性,对移动机器人Summit-XL进行了实验研究。Summit-XL利用摄像头感知周围环境信息,从起点到终点规划全局运动路径,并对全局路径上出现的随机障碍物安全避障。实验中用纸箱代表运动环境中的静态障碍物,并在全局路径上设计随机障碍物(用圈标出),当传感器检测到该障碍物后,机器人利用动态窗口方法局部安全路径规划,实验环境如图8所示。 图8 机器人随机避障实验环境 实验中,机器人规划了全局运动路径,并成功躲避随机障碍物,同时返回全局路径安全运动,实验结果如图9所示。 图9给出了移动机器人在随机障碍物环境下的路径规划结果。由图可知,机器人从起点出发规划全局路径,对全局路径上出现的随机障碍物可安全避障,并继续返回全局路径向目标点移动。实验结果表明,文中提出的改进粒子群方法可规划全局最优运动路径,再结合动态窗口方法可避开随机障碍物,并保障机器人安全返回全局路径,实现了随机障碍物环境下的移动机器人最优安全运动。 研究了随机障碍物环境下的移动机器人最优路径规划问题,通过设计随机数更新粒子的位置和速度并减小区间端点对粒子运动的影响,提出了改进PSO方法规划机器人的全局运动路径;同时对于全局路径上出现的随机障碍物,利用DWA方法安全避障,并使机器人返回全局路径;通过与传统PSO方法仿真对比,改进的PSO方法运行时间减少并且运动路径更短,进一步实验验证了改进PSO算法融合DWA方法的有效性和优越性,为随机障碍物环境下机器人安全避障并返回全局最优路径提供了解决方法。2.3 局部随机障碍物安全避障
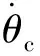
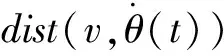

3 仿真分析
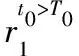

4 实验结果
5 结论

