Novel Sum-of-Sinusoids Simulation Channel Modeling for 6G Multiple-Input Multiple-Output Vehicle-to-Everything Communications

Hao Jiang ,Hongming Zhang ,Ting Liu

1 College of Artificial Intelligence,Nanjing University of Information Science and Technology,210044,China

2 National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China

3 School of Information and Communication Engineering,Beijing University of Posts and Telecommunications,China

Abstract: In this paper,a statistical cluster-based simulation channel model with a finite number of sinusoids is proposed for depicting the multiple-input multiple-output (MIMO) communications in vehicleto-everything (V2X) environments.In the proposed sum-of-sinusoids (SoS) channel model,the waves that emerge from the transmitter undergo line-of-sight(LoS) and non-line-of-sight (NLoS) propagation to the receiver,which makes the model suitable for describing numerous V2X wireless communication scenarios for sixth-generation (6G).We derive expressions for the real and imaginary parts of the complex channel impulse response (CIR),which characterize the physical propagation characteristics of V2X wireless channels.The statistical properties of the real and imaginary parts of the complex CIRs,i.e.,autocorrelation functions(ACFs),Doppler power spectral densities (PSDs),cross-correlation functions (CCFs),and variances of ACFs and CCFs,are derived and discussed.Simulation results are generated and match those predicted by the underlying theory,demonstrating the accuracy of our derivation and analysis.The proposed framework and underlying theory arise as an efficient tool to investigate the statistical properties of 6G MIMO V2X communication systems.

Keywords: complex CIRs;LoS and NLoS propagation components;MIMO V2X communication environments;SoS simulation channel model;statistical properties

I.INTRODUCTION

1.1 Backgrounds

In recent years,the study of sixth-generation (6G)vehicle-to-everything (V2X) communications has been conducted by developing channel simulators for such communication systems[1].The development of V2X wireless channel modeling for 6G communications is indispensable due to its wide adaptability in diverse schemes,wideband wireless communication systems,and multiple-input multiple-output (MIMO)systems [2].Indeed,collecting real-data for studying 6G communication systems is not an easy task.To address this research challenge,it is crucial for researchers to propose effective channel models for characterizing the statistical properties of practical 6G wireless communication systems[3].

1.2 Prior Works

The existing literature[4,5]contains reports on commonly adopted geometry-based stochastic channel modeling for investigating the wireless propagation properties with multiple propagation paths between a transmitter and a receiver.The authors in [6] and [7]developed Rician channel models to describe the mobile communication scenarios with an assumption that the waves emerging from the transmitter undergo lineof-sight(LoS)and non-line-of-sight(NLoS)propagations to the receiver.In[8],Dahech et al.proposed a geometry-based channel model for V2X communications where the propagation links travelling from the transmitter to the receiver are assumed to undergo a single interaction.In this study,they assumed that the surrounding objects are distributed in a uniform manner within a two-ring model between the transceivers.The authors in [9] proposed a multi-bounce scattering channel model to study the statistical characteristics of propagation links in V2X channels,which adopted an elliptical model to depict the spatial distribution of scatterers in mobile radio communication environments.In[10],the authors developed a temporal non-stationary multipath fading channel model for V2X communications,where the transmitter and receiver are subject to changes in their velocities and trajectories.Furthermore,in our previous study in [11],we proposed a MIMO channel model for V2X communications in tunnel scenarios where multiple confocal semi-ellipsoid models were adopted to characterize the statistical properties for different propagation delays.For the sake of investigating the physics-based characteristics of V2X channels in roadside scenarios,Yuan et al.[12]and Jiang et al.[13]developed multiple confocal elliptic-cylinders and cylinder models,respectively,to describe the scatterers distributions of MIMO communications in V2X scenarios.In these studies,the expressions of the channel characteristics for multipaths were derived and investigated.Common to the aforementioned geometric channel models is that statistical propagation properties were derived and investigated based on the assumption that there is an infinite number of effective scatterers over the wireless communication environment.However,in practice,the scatterers distributions are discrete in practical V2X roadside scenarios,therefore we are required to consider statistical sum-of-sinusoids(SoS)channel models with a finite number of sinusoids to study such propagation problems[14].

For multipath fading wireless channels,it is in principle difficult to obtain the information of the orientation and material properties of obstacles between a transmitter and a receiver.This will bring us principle difficulties in evaluating the performance of wireless communication systems,such as channel capacity,throughout,and so on.To solve this issue,in recent years,SoS simulation models have been widely used because of their accuracy and simulation speed[15].Numerous research works have done the simulations and measurements to demonstrate that a finite number of sinusoids has the advantage of approximating a Gaussian process,and therefore leading to reduce the computational complexity.It is worth noting that stochastic channel modeling is on the basis of conducting large numbers of measurements for characterizing the physical properties of wireless channels,and therefore are used to describe a range of communication scenarios by properly adjusting the model parameters [16,17].In the existing literature,such as [18],the authors presented the statistical properties of SoS simulation channel models.The authors in [19] proposed a series of parameter computation methods for the design of SoS Rayleigh fading channel simulators.The authors in [20] proposed an SoS based simulation channel model for a non-isotropic scattering environment that consists of a finite number of scatterers surrounding the transmitter and receiver.In [21],the authors proposed classical Jakes’SoS channel models to study the wireless propagation characteristics.Although the Jakes’Rayleigh fading model and its variants based on SoS provided a simple way for simulations,they posed a major shortcoming of long simulation time in simulating the correlation properties in the space,time,and frequency domains.Furthermore,the statistical properties of deterministic SoS simulation models were studied in [19] for mobile flat fading channels.In [22],the authors proposed another simulation model for fading channels.However,the aforementioned derivations and analysis are required to generate a complex Gaussian process in[22]are relatively complicated.As a result,this algorithm could not be widely extended to other communication systems.Moreover,the authors in[23]presented an improved SoS fading model to generate Rayleigh fading processes while satisfying theoretical independence requirements.The author in [24] proposed a statistical SoS Rayleigh channel model by randomizing the phase of the sine wave,Doppler frequency and amplitude,meanwhile introducing a Rician factor,which provided an efficient solution with which to analyze and process the complex signals in wireless channels.In[24],the investigation was based on Clarke’s model with an assumption that the received signals were distributed in a uniform manner;however,the effects of real propagation environments on the statistical channel characteristics were not considered.Later,Ren et al.[25]presented a statistical SoS Rician fading simulator to study the second-order statistical characteristics of the channel model.However,in [25],they did not consider the issues related to dynamic properties of the transmitters and receivers on the statistical propagation characteristics.Therefore,this model is inapplicable to characterizing practical V2X channels.

1.3 Motivations and Contributions

It is worth mentioning that the research on the channel modeling is required to evaluate the trade-off among the accuracy,complexity,and generality.In the existing literature,the authors mainly derived the complex channel impulse responses (CIRs) to investigate the propagation characteristics of wireless channels[26,27],such as the autocorrelation functions(ACFs),Doppler power spectral densities(PSDs),and crosscorrelation functions(CCFs).Although the investigations of wireless propagation characteristics based on the aforementioned solution are able to achieve high accuracy,their simulation time,which corresponds to the computational complexity,are very long.This will in principle cause trouble for evaluation of the performance of V2X communication systems,especially for the towards big data communication systems for 6G.To solve this research problems,we are required to design an efficient channel modeling solution for characterizing the physical properties of propagation links in V2X wireless channels for 6G.It is well known that the expressions of the complex CIRs of wireless channels can be separated into real and imaginary parts,which have the abilities to capturing the main physical properties of wireless channels from different perspectives.In light of this,it is reasonable for us to derive the real and imaginary parts of the complex CIRs to probe the V2X channel characteristics.Subsequently,the correlation properties of the real/imaginary parts of the complex CIRs should be derived and discussed.To achieve this goal,we propose an SoS simulation channel model with a finite number of sinusoids,which aims to reducing the computational complexity and simulation time to investigate the V2X channel characteristics.The major contributions and novelties of this paper are summarized as follows:

• We derive expressions for the real and imaginary parts of the complex CIRs of V2X channel models.The underlying statistical properties of the real and imaginary parts of the proposed SoS channel model include the ACFs,CCFs,Doppler PSDs,and variances of ACFs and CCFs.This provides us with new guidance for characterizing the physical properties of propagation characteristics in V2X wireless channels.

• We present an SoS channel model that considers both the LoS and NLoS propagation links for V2X communication environments.By introducing a Rician factor,we provide a statistical SoS simulation model to build a valid Rician fading simulator.

• Moreover,we investigate the ACFs of the real/imaginary parts of the complex CIRs for the LoS and NLoS propagation links.Furthermore,we study the CCFs between the real and imaginary parts of the complex CIRs for different propagation links.Comparisons show that the investigations of the statistical properties of V2X channel models based on the proposed algorithm has the advantage of low simulation complexity when investigating channel characteristics compared to methods described elsewhere.

• We analyze the statistical properties of the proposed SoS channel model in terms of the different Rician factors and motion velocities of the transmitter and receiver.The simulation results corroborate the analytical findings.

The remainder of this paper is organized as follows.Section II describes the system channel model for MIMO communications in V2X environments.In Section III,we present a statistical SoS simulation model with a finite number of sinusoids to study the statistical properties of V2X channel models.In Section IV,numerical results are presented.We conclude our work in Section V.

II.CHANNEL MODEL AND DESCRIPTION

Let us consider an SoS simulation model for describing 6G MIMO V2X communication channels,as shown in figure 1,with MTantennas at the transmitter and MRantennas at the receiver [28].The signal received at the receiver is a superposition of the LoS and NLoS propagation links,where the latter ones indicate that the waves are scattered through the clusters.In the proposed channel model,we assume that the cluster is within N sub-paths,and these sub-paths with different propagation delays are uncorrelated.Specifically,neither the sub-paths between two different LoS propagation links,the sub-paths between two different NLoS propagation links,nor the sub-paths between the LoS and NLoS propagation links,are uncorrelated.It is worth mentioning that the waves emitted from the transmitter undergo multiple ray-paths within the cluster before arriving at the receiver;however,we only represent the n-th(n=1,2,...N)ray-path within the cluster in figure 1 for clarity[29].

The physical properties of the V2X channels can be characterized by a complex matrixH(t)=of size MR×MT,where p and q denote the transmit and receive antenna indexes.The hpq(t) is the complex CIR between the p-th (p=1,2,..,MT) antenna of the MT array and q-th (q=1,2,..,MR)antenna of the MR array[30].This means that the hpq(t) can be used to capture the physical properties of the propagation components can be characterized by setting different indexes of the transmit and receive antennas.In the V2X channel model,we assume that the LoS and NLoS propagations rays are mutually independent,and therefore the hpq(t)can be written by[31]

where ζ=2π/λ and λ is the carrier wavelength,K denotes the Rician factor,fcis the carrier frequency,vTand vRare the motion speeds of the transmitter and receiver,respectively;ηTand ηRare the motion directions of the transmitter and receiver,respectively;are the angle of departure(AoD)and angle of arrival (AoA) associated with the n-th(n=1,2,...,N) ray within the cluster,respectively;denote the AoD and AoA of the LoS propagation links,respectively.The φ0is the initial phase of the NLoS propagation rays,which is assumed to follow a uniform distribution over [−π,π).The τpqin(2)stands for the delay of the LoS propagation paths,which can be derived by computing the ratio of the propagated distance to the light speed c.It is well known that when the variable ϵ is extremely small,we can obtain sin ϵ ≈0 and cos ϵ ≈1.Therefore,the expression of the distance τpqcan be expressed as

where ψTand ψRaccount for the orientations of the transmit and receive antenna arrays,respectively.The δTand δRare,respectively,the adjacent spacings between two different antenna elements at the transmitter and receiver.The D0represents the distance associated with the central points between the transmit antenna array and the receive antenna array [36].In Eq.(3),τpq,nis the delay of the propagated waves from the p-th antenna impinge on the cluster via the n-th ray before reaching the q-th antenna,whose expression can be approximated in (5),where ξT,nand ξR,ndenote the central positions of the transmit and receive antenna arrays associated with the n-th ray of the cluster,respectively.

III.A NOVEL SOS RICIAN FADING SIMULATOR

In this section,the expressions of the complex CIRs of V2X channels are separated into the real and imaginary parts based on the Euler’s theorem.It is noteworthy to mention that the real and imaginary parts have the abilities to determining the main physical properties of propagation links in V2X channels from different perspectives.Doing this,it becomes essential to study the statistical properties of the real and imaginary parts of the complex CIRs.In particular,through the study of the ACFs of the real and imaginary parts of these complex CIRs,the CCFs between the real and imaginary parts of the complex CIRs are found.

The normalized low-pass fading process of the proposed SoS statistical simulation model in(1)is rewritten thus:

The authors in [24] studied the statistical propagation properties of Rician fading channels,i.e.,ACFs and CCFs of complex CIRs,for the case when the number of sinusoids N approaches infinity,however,since the distributions of the obstacles between the transmitter and receiver are discrete in wireless channels,we are required to investigate a statistical SoS simulation channel model with a finite number of sinusoids for MIMO communications in V2X scenarios.To justify the suitability of the proposed wireless channel models as a valid Rician fading simulator[37],we study the statistical properties of the complex CIRs in the following subsection.

In the proposed V2X channel model,when the N approaches infinity,the discrete angular parametersare respectively updated by their continuous counterparts αTand αR.In the existing literature [38],von Mises probability density function(PDF)has been widely used for describing the scatterers distributions in practical wireless communication scenarios,which expression can be given by[39]

where α follows a uniform distribution in the interval−π to π.I0denotes the zeroth-order modified Bessel function of the first kind[40],µαrepresents the mean value of the angle α,and k (k＞0) is obtained by averaging the angular value of theµα.Since the positions of scatterers are not fixed in practical V2X communication scenarios,the propagation delay τ varies as different values of the propagation distances from the transmitter/receiver to the scatterers.Considering this,we define τ as independent variables of the expressions of the ACFs,CCFs,and variances of ACFs and CCFs in the following parts.

3.1 ACFs and CCFs of the Complex CIRs

In the proposed SoS simulation channel model,the ACF of the real part of the complex CIRs can be derived by using(7)and(8)as follows:

where E[·]denotes the expectation operation,and

In the following,by using(9)and(10),the ACF of the imaginary part of the complex CIRs is expressed as

where

In V2X channels,the received signal frequency constantly vary on account of the motion of the transmitter and receiver.Let us take the Fourier transform of the temporal ACFin(14)with respect to the propagation delay τ,we can write the expression of the Doppler PSD as[26]

where ν stands for the Doppler frequency.

Furthermore,by using (7)-(10),the CCF between the real and imaginary parts of the complex CIRs can be written by

Details of the derivation of(17)are provided in Appendix A.In addition,we can obtain

3.2 Ensemble Averaging ACFs and CCFs

The ensemble averaging ACF of the real parts of the complex CIRs can be written by

It is worth noting that the ensemble averaging ACFof the imaginary parts of the complex CIR can be derived in a manner similar to that expressed in (19),i.e.,.The proof is therefore omitted here for brevity.Furthermore,the ensemble averaging CCF between the real part and imaginary part of the complex CIR is given by

According to (19)-(20),we can notice that the ensemble averaging ACFs and CCFs are related to the number of the sinusoids N and Rician factor K.

3.3 Variances of the Ensemble Averaging ACFs and CCFs

In order to estimate the accuracies of the above ensemble averaging ACFs and CCFs,the variances of the ensemble averaging correlation statistics are demonstrated.In the proposed channel model,the variance of the ensemble averaging ACFof the real part of the complex CIR of such channel model in(19)is expressed as

By substituting (22) into (21),we can simplify theas

By substituting Eqs.(12) and (19) into (23),the variance of the ensemble averaging ACFis expressed as follows:

It is observed that the variance of the ensemble averaging ACFin (24) is related to the N and K.To be specific,when the N tends to infinity,the ensemble averaging ACF tends to be the time averaging ACF.

Furthermore,the variance of the ensemble averaging CCFis expressed as

According to Eqs.(21)-(25),the variances of the ensemble averaging ACFand CCFare not related to t,but are related to τ.

IV.STATISTICAL PROPERTIES OF THE CHANNEL MODEL

In the existing literature,the complex CIRs of wireless channel models have been widely derived for describing the statistical properties of the propagation characteristics of wireless communication systems [41].In these studies,the authors respectively adopted the CCFs and ACFs to quantify the correlations properties of the propagation links between a transmitter to a receiver in the space and temporal domains.In light of this,we follow this research solution in the following parts.In the proposed V2X channel model,the spatial CCF between the propagation link from the p-th antenna to the q-th antenna,as well as the link from the p′-th (p′=1,2,...,MT) antenna to the q′-th (q′=1,2,...,MR) antenna can be measured by computing the correlation between the complex CIRs hpq(t)and,which can be written by[42,43]

where (·)∗denotes the complex conjugate operation.As mentioned before,the real/imaginary parts of the complex CIRs in Rician channels are used to characterize the main physical properties,therefore one needs to study the correlation of the real/imaginary parts for investigating the correlations between different propagation links.Considering this,by substituting (7) into (26),the CCFs between the real parts of the complex CIR for different direct propagation links can be given by

By substituting (9) into (26),the CCF between the imaginary parts of the complex CIR for different direct links is expressed as

It is well known that the direct propagation links between the transmitter and receiver are not impacted by the number of scatterers within the cluster,which implies that the CCFs in(27)and(28)do not depend on the N.In light of this,the ensemble averaging CCFs between the real/imaginary parts of the complex CIRs for different direct links is written by

By plugging(8)into(26),the CCF between the real parts of the complex CIRs for the NLoS propagation link from the p-th antenna to the q-th antenna,as well as the NLoS propagation link from the p′-th antenna to the q′-th antenna,can be written by

In this case,the variance of the ensemble averaging CCFis given by

Let us we substitute(10)into(26),the CCF between the imaginary parts of the complex CIR for the NLoS propagation link from the p-th antenna to the q-th antenna,as well as the NLoS propagation link from the p′-th antenna to the q′-th antenna,can be expressed as

In this case,the variance of the ensemble averaging CCFis given by

In addition,the variance of the ensemble averaging

According to the expressions in (32) and (35),we note that the variances of the ensemble averaging CCFsfor different NLoS propagation links are related to N and K,which will be simulated and discussed in the next section.

V.RESULTS AND DISCUSSIONS

In this section,analytical results of important statistics are illustrated according to the derived expressions in Section IV.Some of the propagation characteristics including the CCFs and ACFs are compared with the corresponding channel measurement data.However,in the following simulation,the parameters such as carrier frequency,antenna height,transmitter-receiver separation,and motion velocity of the transmitter/receiver are set according to the corresponding measurements.Only a small number of parameters,such as K,φT,and φR,which differentiate the proposed V2X channel model as compared to conventional ones,are determined by fitting statistical properties to the channel measurement data.The rest of parameters are randomly generated according to the 3GPP TR38.901 channel model.Furthermore,simulation results of the propagation characteristics are presented and discussed with the same initial phase of the NLoS propagation links[−π,π),but different degrees of randomness are used for testing.

Figure 2 shows the ACFs between the real parts of the complex CIRs of V2X channels,i.e.,,for different numbers of sinusoids.It is obvious that lower values of the ACFs are resulted from a larger propagation delay τ,which are in agreements with the results in[24],verifying the correctness of the simulations and derivations in (12).Another interesting phenomenon is that when the N increases from 2 to 8,and even to a higher value,the values of the ACFs decrease as the τ increases from 0 to 5.The simulation results are in agreement with the analytical results,which verify the correctness of the ACFs between the real parts of the complex CIRs of V2X channels.

It is well known that the power of the LoS and NLoS propagation links are impacted by the Rician factor K.This can be interpreted by the fact that when the power of the NLoS components is small,the noise and interference have little impacts on the V2X channel modeling;otherwise,the impact is extremely small and as a consequence,the V2X channel modeling performance is relatively well,which is in consistent with the simulation results in[27].Figure 3 shows the ACFs of the channel model,i.e.,,for different values of the parameter K and different directions of motion of the transmitter and receiver(i.e.,ηTand ηR).It can be observed from Figure 3(a) and (b) that when the direction of motion changes from ηT=11π/12 and ηR=π/12 to ηT=π/12 and ηR=11π/12,the amplitude of the ACFs change with different values of K.Similar behaviors can be found in Figures 3(c)and(d).It is also can be found that the ACFs decrease slightly as the time difference delay τ increases,which confirms the observations in [29],thereby validating the accuracy of the aforementioned analysis.Furthermore,by noting the curves in Figure 3(a)and 3(c),we can find that the amplitudes and periods of the curves of the ACFs vary with changes to the motion directions of the transmitter and receiver.

It is worth mentioning that the proposed V2X channel model has the advantage of well generality to describing a variety of high dynamic scenarios,such as vehicle-to-vehicle (V2V) communications,by properly adjusting the model parameters.Since V2V communications have received great attention in the field of channel modeling in recent years [1],in Figure 6,we study the Doppler PSDs of V2V channel models for different motion time of the MT and MR.It can be seen from the figure that the Doppler spectrum of V2V channels has different behaviors at different motion time of the transmitter and receiver,which are in agreements with the measurements in [26].Another interesting phenomenon is that the Doppler spectrum has a dominant narrow peak at the zero frequency,which agrees with the theoretical simulations in [44]and the measurements in [45],verifying the correctness of the simulations and derivations in(23).

In Figure 8,we study the CCFs between the real parts of the complex CIRs of V2V channels for different motion velocity/direction of the MT and MR.It is obvious that when the ratio of the propagation distances to the light speed increases,especially for a large propagation delay τ,the CCFs decrease gradually.The above observation fits very well with the results concluded by the measurements in [12],thereby demonstrating the accuracy of the derivations and analysis of the CCFs in Figure 8.Furthermore,we note that when the MT and MR move toward each other,i.e.,φT=π and φR=0,the values of the correlation properties between two different propagation links are obviously higher than those when the MT and MR move in opposite directions,i.e.,φT=0 and φR=π.In addition,the simulation results show that the motion velocities of the MT and MR play a role in the V2V channel propagation characteristics.Notice that the CCFs of V2V channel models vary more significantly as the motion velocity rises from 5 m/s to 20 m/s.

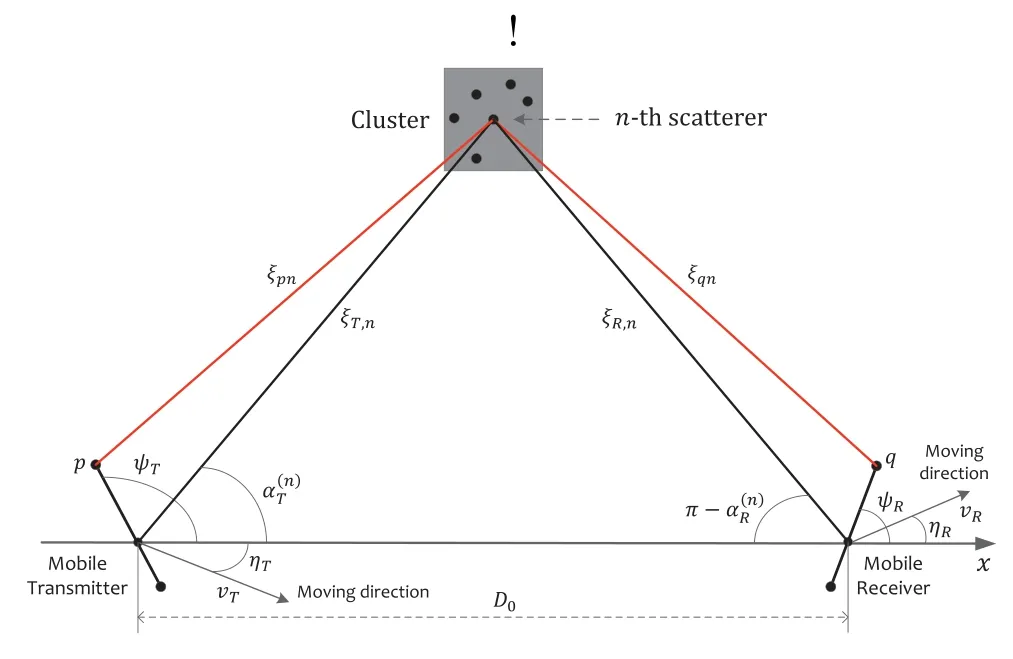
Figure 1. Illustration of the proposed SoS simulation channel model for V2X MIMO communication environments.

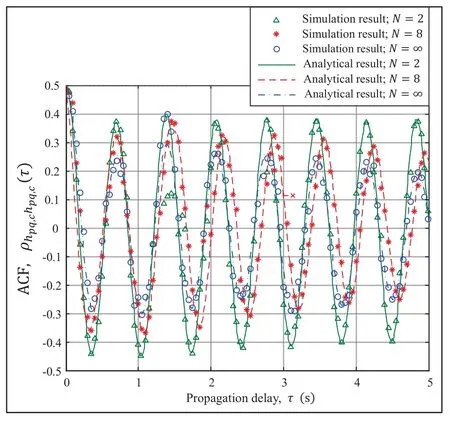
Figure 2. Simulated and analytical results of the ACFs of the real parts of the complex CIRs of the channel model in terms of N when fc=5.4 GHz,D0=100 m,vT=vR=10 m/s.(a) ηT=11π/12,ηR=π/12;(b) ηT=π/12,ηR=11π/12;(c)ηT=5π/6,ηR=π/6;(d)ηT=π/6,ηR=5π/6.

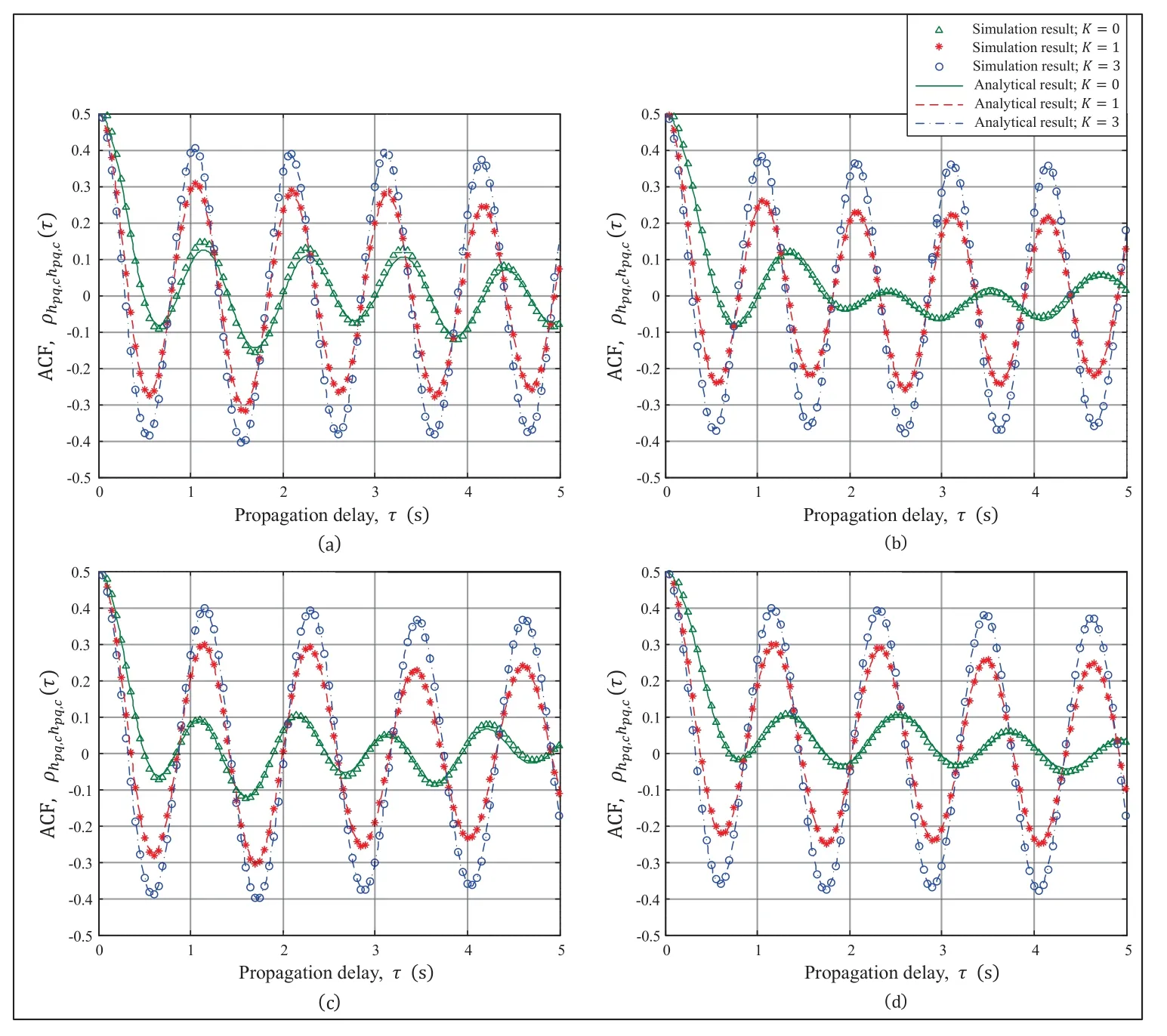
Figure 3. Simulation and analytical results of the ACFs of the real parts of the complex CIRs of the channel model in terms of the Rician factor K and motion directions ηT and ηR when fc=5.4 GHz,D0=100 m,vT=vR=10 m/s.(a)ηT=11π/12,ηR=π/12;(b)ηT=π/12,ηR=11π/12;(c)ηT=5π/6,ηR=π/6;(d)ηT=π/6,ηR=5π/6.

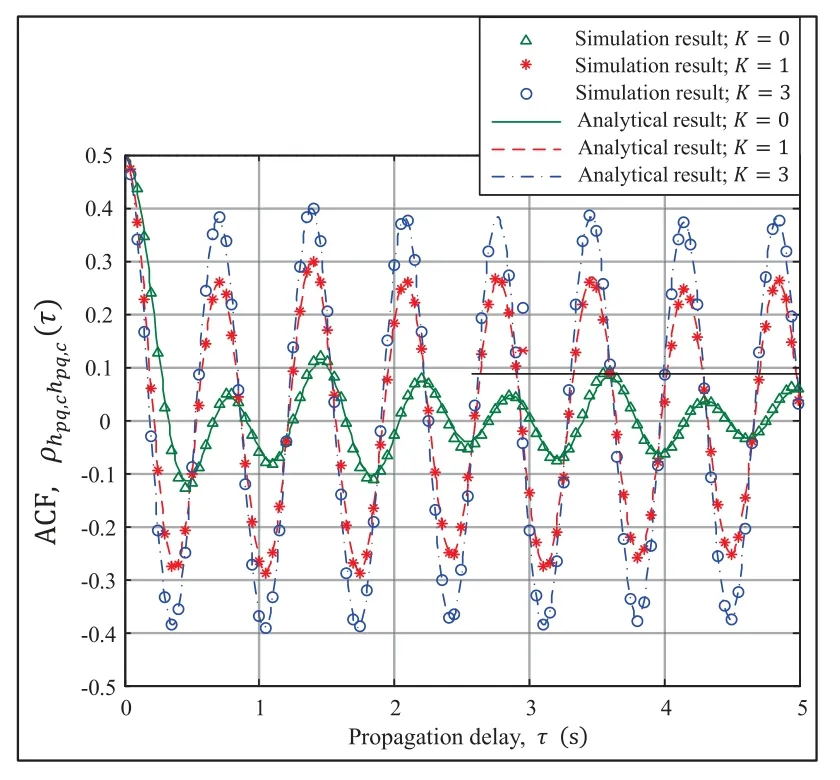
Figure 4. Simulated and analytical results of the ACFs of the real parts of the complex CIRs of the channel model in terms of the parameter K when fc=5.4 GHz,D0=100 m,vT=10 m/s,vR=20 m/s,ηT=11π/12,and ηR=π/12.

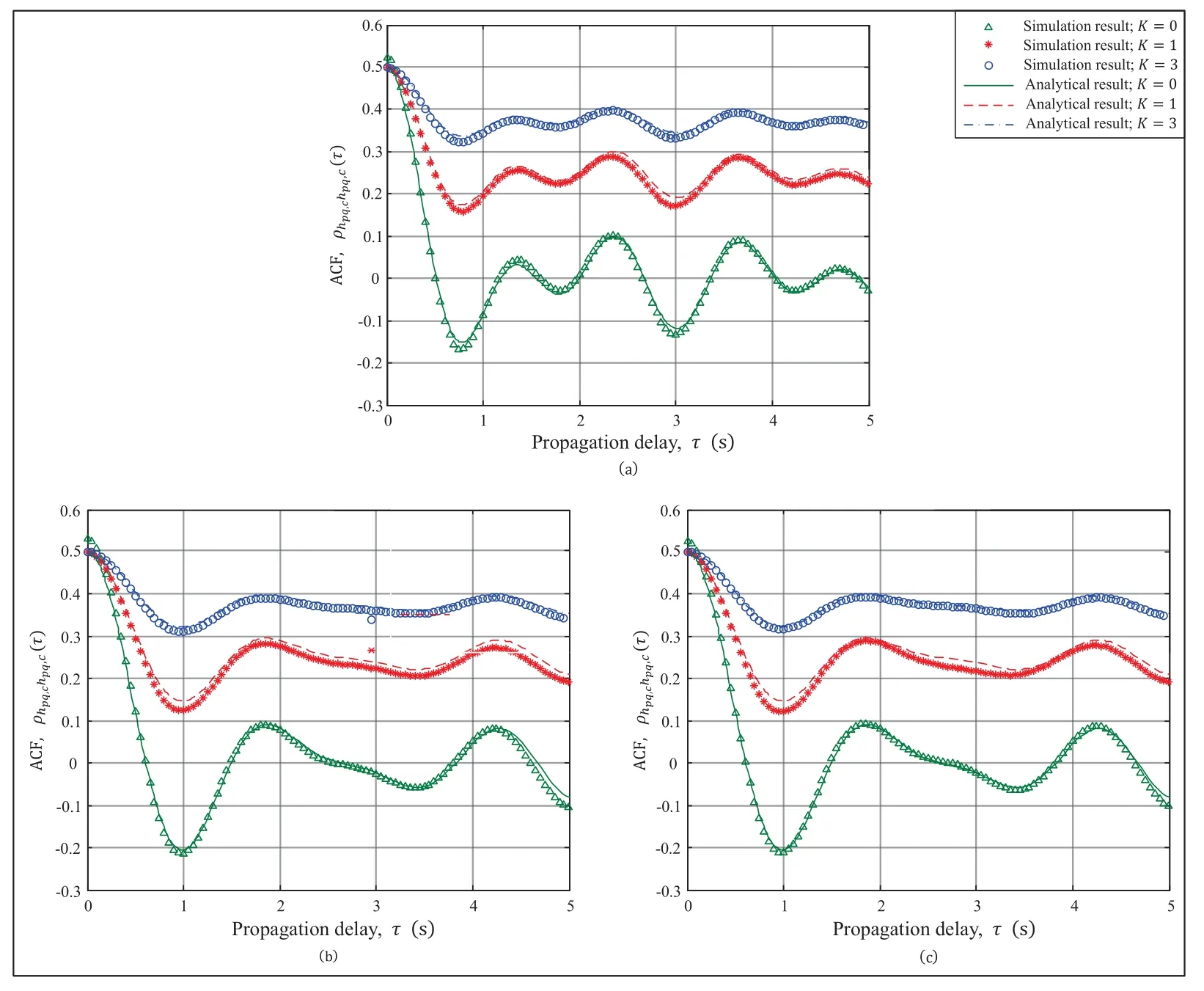
Figure 5. Simulated and analytical results of the ACFs of the real parts of the complex CIRs of the channel model in terms of the parameter K and different directions of motion ηT and ηR when fc=5.4 GHz,D0=100 m,vT=vR=10 m/s.(a)ηT=ηR=π/3;(b)ηT=−π/2,ηR=π/2;(c)ηT=π/2,ηR=−π/2.

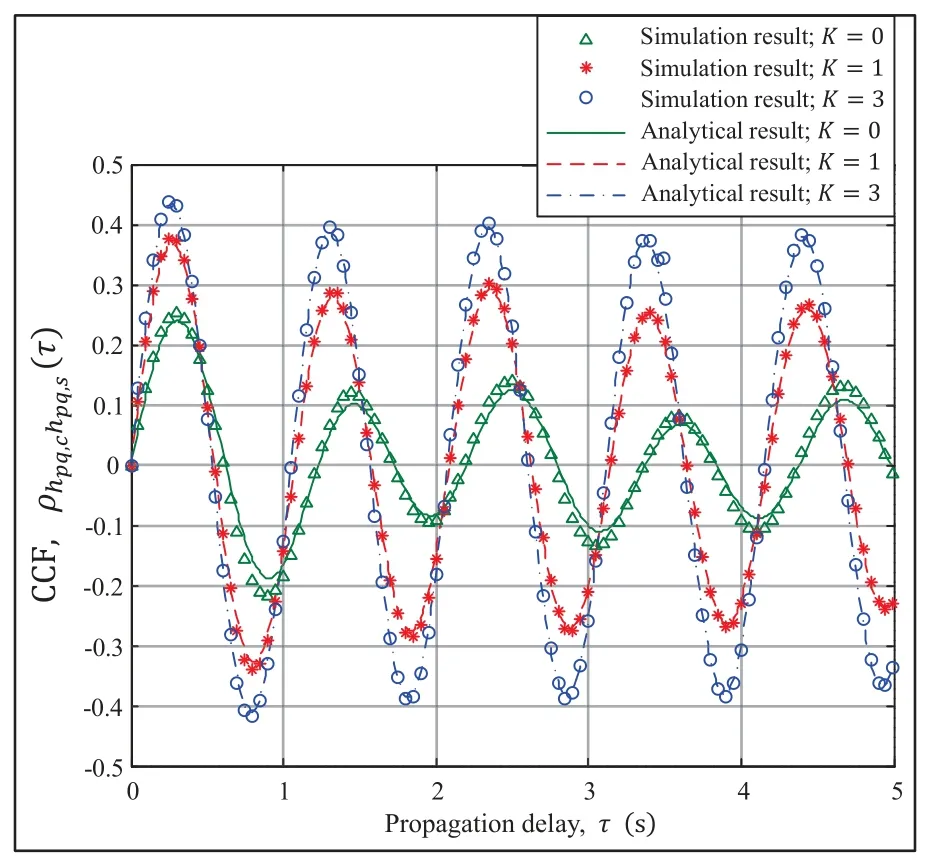
Figure 7. Simulated and analytical results of the CCFs between the real and imaginary parts of the complex CIRs of the channel model in terms of the parameter K when fc=5.4 GHz,D0=100 m,vT=vR=10 m/s,ηT=11π/12,and ηR=π/12.

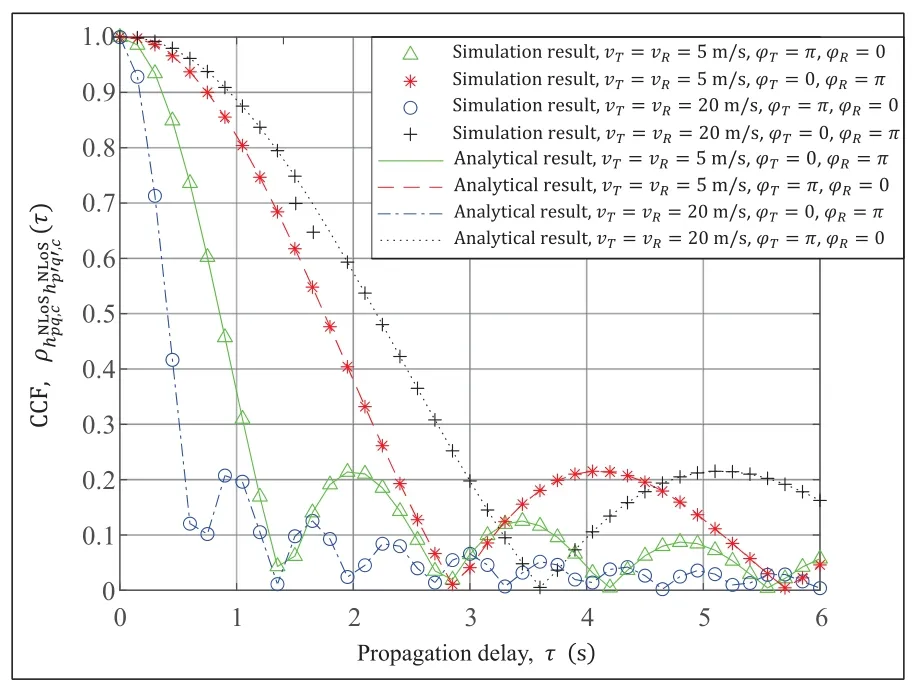
Figure 8. Simulated and analytical results of the CCFs in terms of the directions of motion of the transmitter and receiver when fc=5.4 GHz,D0=100 m and vT=vR=10 m/s.

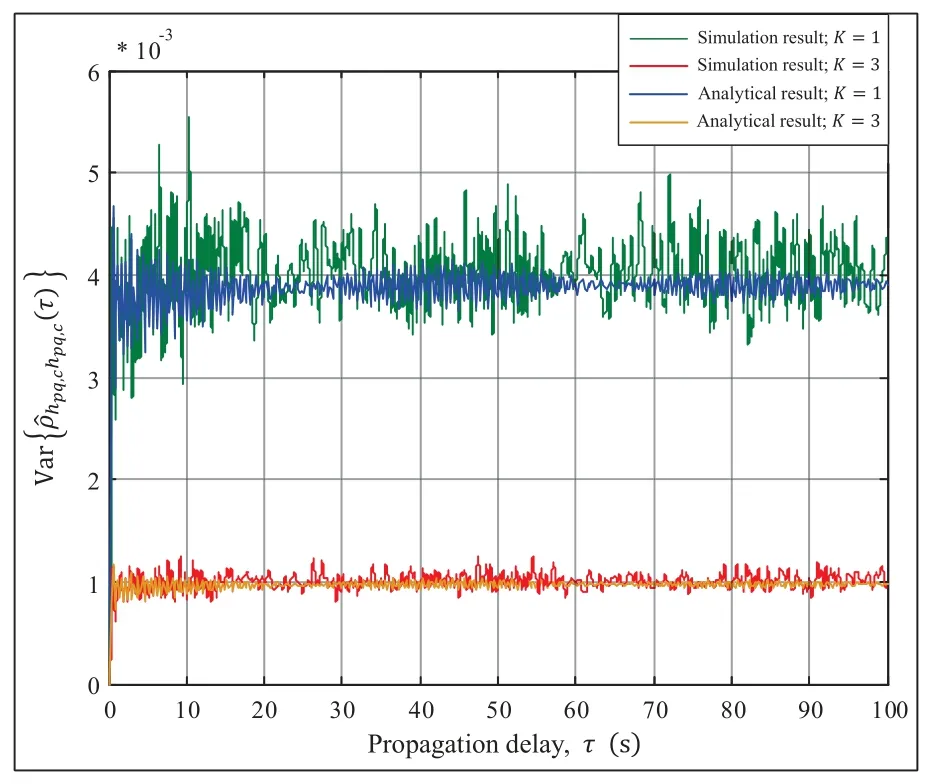
Figure 9. Simulated and analytical results of the variances of the ensemble averaging ACFs of the channel model in terms of the parameter K when fc=5.4 GHz,D0=100 m,vT=vR=10 m/s,ηT=11π/12,and ηR=π/12.

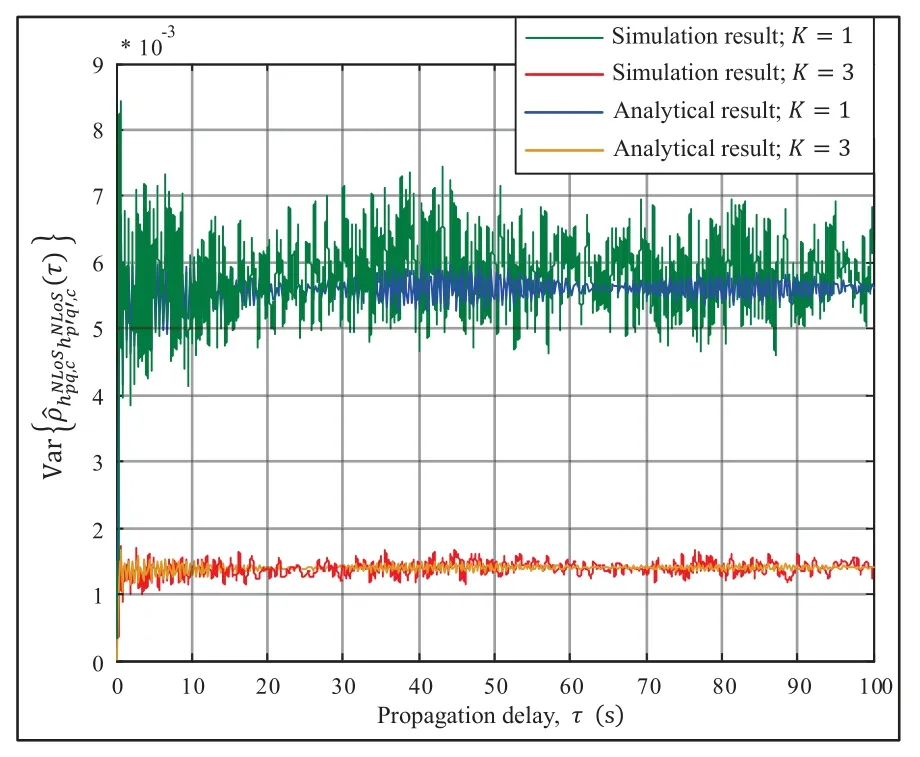
Figure 10.Simulated and analytical results of the variances of the CCFs for different NLoS rays in terms of the parameter K when fc=5.4 GHz,D0=100 m,and vT=vR=10 m/s.

In Table 1,we compare the simulation time of investigating the propagation characteristics of V2X channels based on the proposed method and conventional ones.It can be seen that the simulation time of investigating the V2X channel characteristics using the real/imaginary parts of the complex CIRs is obviously shorter than that of the conventional methods using the complex CIRs directly,which shows that the proposed scheme has the ability to achieving better computational efficiency than the existing ones.

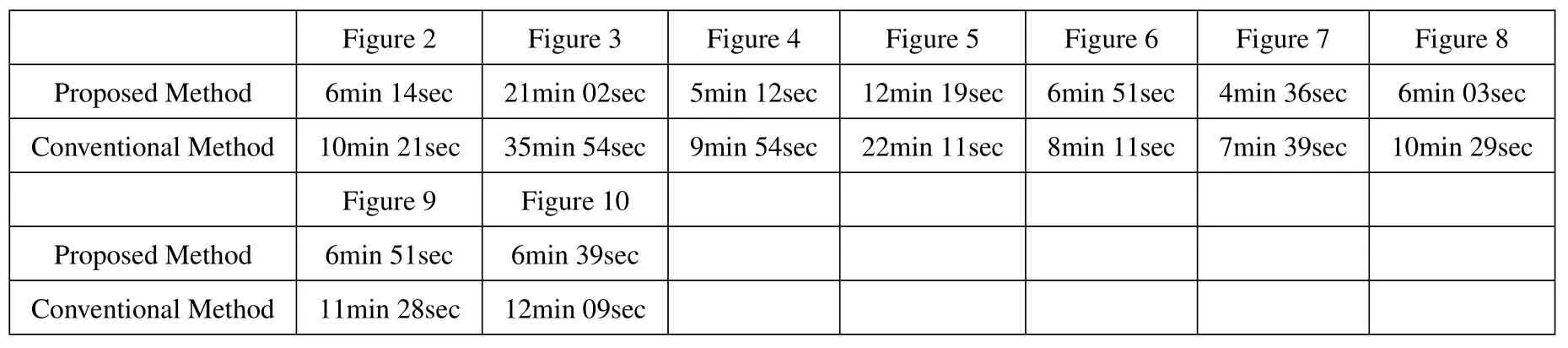
Table 1. Comparisons of the simulation time between the proposed methods and conventional ones.

VI.CONCLUSION

We have provided an SoS simulation channel model with a finite number of sinusoids for MIMO communications in V2X scenarios.We provide an efficient solution with low computational complexity for investigating the channel characteristics.Numerical results have validated that the ACFs of the real/imaginary parts of the complex CIRs decrease slightly as K is increased.Furthermore,the CCFs of the real/imaginary parts of the complex CIRs for different NLoS propagation links exhibit different behaviors as the directions of motion of the transmitter and receiver vary.From the results,we have observed that the proposed solution exhibits less complexity than the state-of-the-art model.Finally,the simulated results provide a close match to our theoretical findings.As future work,we can point out two potential directions: (i) extend the proposed algorithm for massive MIMO communication systems,and(ii)conduct measurements to further validate the effectiveness of the proposed algorithm.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China (NSFC) (No.62101274 and 62101275),Natural Science Foundation of Jiangsu Province(BK20210640),and Open Research Fund of National Mobile Communications Research Laboratory Southeast University under Grant 2021D03.

APPENDIX

A Appendix A:Proof of the CCF in (17)

The proof of the CCF between the real and imaginary parts of the complex CIRs of the proposed V2X channel model in(17)is outlined in the following parts.We have

Herein,we derive the specific expressions of the four terms on the right-hand side of(A.1).To be specific,the CCF between the real and imaginary parts of the complex CIRs for the direct link between the p-th antenna to the q-th antenna is given by

In the proposed channel model,we observe that the real part of the complex CIRs for the direct link and the imaginary part of the complex CIRs for the NLoS propagation link are mutually independent.Meanwhile,the imaginary part of the complex CIRs for the direct link and the real part of the complex CIRs for the NLoS propagation link are also mutually independent.Therefore,we have

Finally,the CCF between the real and imaginary parts of the complex CIRs for the NLoS propagation link between the p-th antenna to the q-th antenna is expressed as

By substituting Eqs.(A.2)-(A.5) into (A.1),the CCF between the real and imaginary parts of the complex CIRs of the proposed model can be written by

This completes the proof of the derivation in(17).