Cluster-Based Massive Access for Massive MIMO Systems

Shiyu Liang ,Wei Chen ,Zhongwen Sun ,Ao Chen ,Bo Ai

1 State Key Laboratory of Advanced Rail Autonomous Operation,Beijing Jiaotong University,Beijing 100091,China

2 School of Electronic and Information Engineering,Beijing Jiaotong University,Beijing 100091,China

3 Frontiers Science Center for Smart High-speed Railway System,Beijing Jiaotong University,Beijing 100091,China

4 Key Laboratory of Railway Industry of Broadband Mobile Information Communications,Beijing Jiaotong University,Beijing 100091,China

5 Beijing Engineering Research Center of High-speed Railway Broadband Mobile Communications,Beijing Jiaotong University,Beijing 100091,China

6 School of Information Engineering,Zhengzhou University,Zhengzhou 450001,China

Abstract: Massive machine type communication aims to support the connection of massive devices,which is still an important scenario in 6G.In this paper,a novel cluster-based massive access method is proposed for massive multiple input multiple output systems.By exploiting the angular domain characteristics,devices are separated into multiple clusters with a learned cluster-specific dictionary,which enhances the identification of active devices.For detected active devices whose data recovery fails,power domain nonorthogonal multiple access with successive interference cancellation is employed to recover their data via re-transmission.Simulation results show that the proposed scheme and algorithm achieve improved performance on active user detection and data recovery.

Keywords: compressive sensing;dictionary learning;multiuser detection;random access

I.INTRODUCTION

With the commercialization of 5G,research on 6G has gained significant attention.Compared to the performance indicator of 1 million connections per square kilometer in 5G,6G claims an ultra-high density performance indicator with a device connection density of over 100 per cubic meter,aiming to achieve nearly seamless global connectivity for air,sky,earth,and sea [1,2].Massive machine-type communication(mMTC)aims to support sporadic transmission of small data packets by machine-type devices (MTDs),and is a key part of realizing ubiquitous communication [3].However,in the traditional grant-based random access(RA)scheme,MTDs need the grant from the base station (BS) before sending data,which includes several interactions and causes significant signaling overhead.Compared to the small data packets of MTDs,such signaling overhead is intolerable and causes a waste of resources.In addition,as many MTDs are battery-operated with limitted power,multiple interactions in handshake reduce their lifetime.

In order to reduce the high control signaling overhead between the access phase and data transmission phase,grant-free RA(GFRA)schemes have attracted broad attention in recent years[4–6].In GFRA,MTDs directly send the data along with the pilot instead of waiting for a response/grant from the BS.Due to the sporadic activity of MTDs in the mMTC system,compressive sensing-based multiuser detection (CSMUD) has been proposed for detecting active users and recovering their data [7–9].Specifically,CSMUD consists of two phases.In the first phase,the BS performs active user detection (AUD) and channel estimation based on the pilot sent by the user.In the second phase,the BS utilizes the estimated channel to recover the data.Many CS-MUD algorithms have been proposed to improve the performance of AUD and data recovery [10–14].An enhanced block coordinate descend (BCD) algorithm is proposed in[10],which incorporates a novel candidate set pruning mechanism into the original BCD framework and leads to remarkable CS-MUD performance improvement.The use of sinusoidal spreading sequences is explored in[11].Compared with the random or Zadoff-Chu spreading sequences,using sinusoidal spreading sequences allows some non-iterative algorithms to be utilized in CS-MUD.Besides,various kinds of prior information have been applied to enhance CS-MUD.For example,the activity pattern of adjacent time slots can be exploited in the CS-MUD algorithm design.Dynamic CS-MUD(DCS-MUD)in[12]takes the information of the former time slot as prior information.Then,the bidirectional DCS-MUD (BD-DCS-MUD)proposed in[13]further exploits the prior information of both former and later time slots.The information of modulation and cyclic redundancy check is exploited in CS-MUD to improve the accuracy of pilot detection and data recovery[14].

Furthermore,it has been proved that increasing the number of antennas at the BS enhances CS-MUD[15–18].The existing CS-MUD methods for massive multiple input multiple output(mMIMO)systems mostly treat the CS-MUD as a row-sparse recovery problem[14,15,19],which leads to improved recovery performance in comparison to the conventional elementsparse recovery problem in the single antenna case.Owing to the limited scattering in the environment,the channel of MTDs is also sparse in the angular domain.In specific,each MTD only has a limited number of paths,which leads to the power spectrum density spanning a small range in the angular domain.By exploiting the angular domain channel characteristics,a novel structural based model for massive random access in mMIMO systems is proposed to enhance the performance of AUD and channel estimation in CSMUD[16].However,if two MTDs with the same pilot sequence are close to each other,it is still unable to differentiate them in the angular domain and this kind of collision is difficult to resolve.

In this paper,we propose a new massive access method that exploits the angular domain channel characteristics in mMIMO systems to enhance the performance of CS-MUD.Different from the approach in[16],we propose to separate MTDs into several clusters.MTDs within the same cluster are difficult to differentiate in the channel spatial or angular domain,and are assigned with different pilots to avoid collisions.MTDs in distinct clusters can be differentiated in the channel spatial or angular domain,so pilots are reused across different clusters.To accurately differentiate MTDs from different clusters,we propose to learn a cluster-specific dictionary.Under the learned dictionary,the spatial channel has more prominent block sparse characteristics.When an MTD is active,it directly sends the pre-assigned pilot and data.The BS performs AUD,channel estimation and data recovery using the learned dictionary and the proposed corresponding algorithm.For detected active MTDs whose data recovery fails,as the BS already knows their activity,we exploit power domain nonorthogonal multiple access(PD-NOMA)with successive interference cancellation (SIC) to recover their data via retransmission.Numerical results demonstrate the superiority of the proposed method against conventional methods.

The rest of the paper is organized as follows: Section II describes the system model and the proposed cluster-based CS access scheme.Section III provides the receiver algorithm designed to conduct clusterbased dictionary learning,AUD,channel estimation,and PD-NOMA.Numerical results are presented in Section IV,followed by conclusions in Section V.

II.SYSTEM MODEL AND THE PROPOSED CLUSTER-BASED CS ACCESS SCHEME

We consider a typical mMTC scenario containing a BS equipped withMantennas andNstationary singleantenna MTDs.Nactdevices are active in a coherence time,i.e.,have messages to transmit,and perfect synchronization is assumed in this paper.The spatial MIMO channel described in[20]is considered,which is affected by the geometry characteristics of the cell scattering.For the active MTDk,the spatial MIMO channel is given as

whereNcandNsdenote the number of scattering clusters and the number of propagation subpaths,respectively.Scattering clusters includeNuprimary clusters andNffar scattering clusters (FSCs),and thusNc=Nu+Nf.βi,j,kis the gain of thel-th subpath of thei-th scattering channel cluster of thek-th MTD.α(θi,j,k)=is the array response vector,whereθi,l,kis the angle of arrival(AOA)of thel-th path of the MTDk,and the antenna spacingdis set as half-wavelength,i.e.,d=.The limited scattering clusters restricts the AOAs,and thus the channel becomes sparse in the angular domain.

To support more devices with limited resources,we propose a cluster-based alternating access scheme,which is illustrated in Figure 1.Based on the angular information of MTDs,we separate stationary MTDs into 2Cclusters,whereCis the number of cluster allowed to access in one frame,so half of the clusters are served in one frame.To avoid the influence caused by angle spread between adjacent clusters,we allow non-adjacent clusters to access in one frame.In specific,the BS emits beams of different angles in different frames,and each MTD’s cluster index is determined by the beam index,where it has the strongest receive signal strength.Besides,all clusters share the same pilot pool,and MTDs within the same cluster are pre-assigned with different pilots.Actually,MTDs can randomly select pilots to send,but intra-cluster collision needs to be resolved.Here,we consider the scenario of pre-assigned pilots for simplicity.As pilots are reused in different clusters,the number of needed pilots in the proposed scheme isof that in traditional non-cluster based scheme,which can reduce inter-pilot interference and improve the performance.Although collision may happen between nonadjacent clusters,collided MTDs could be differentiated by their AOAs,i.e.,the sparse structure of channel representation in the angular domain.Without loss of generality,we consider the AUD and data recovery problem for one frame in the sequel.

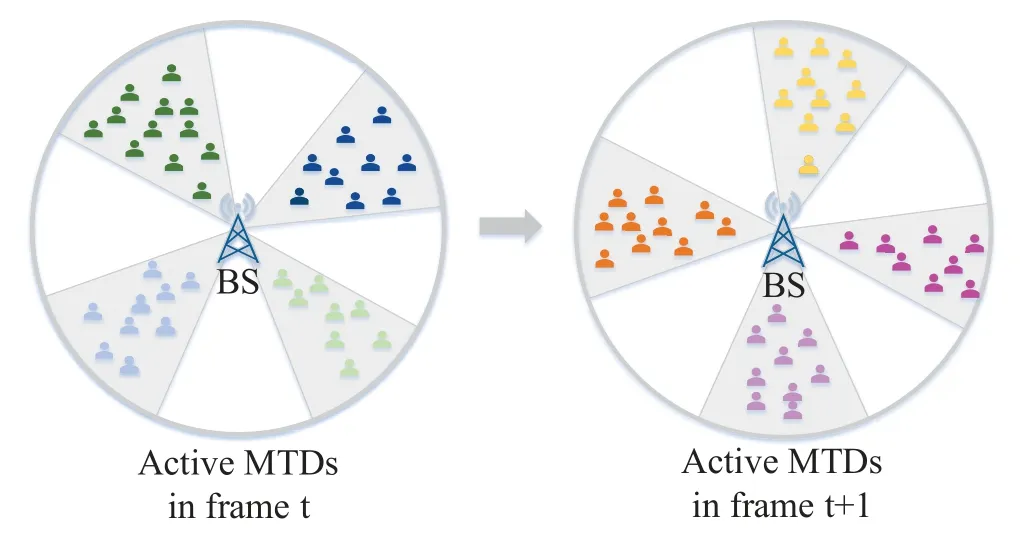
Figure 1. Cluster-based alternating access scheme.

LetP=denote the pilot pool,whereLpandNpare the length and the number of pilots,respectively.Elements in the pilot can be generated randomly followingCN(0,).Corresponding to each pilot,there is a unique spreading sequence for data transmission,which is denoted asS=,whose elements can be generated randomly followingCN(0,).Each active MTD directly transmitsLppilot symbols and multiple data symbols to the BS.The BS first detects transmitted pilots and estimates the channel,then performs data recovery with the estimated channel.

DefineKas the index set of active MTDs.pkandhkdenote the pilot and channel of the MTDk∈K,respectively.Then,the received pilotYp∈at the BS is

whereH=andNp∈denote the channel matrix and the white Gaussian noise matrix,respectively.hpis the superposition channel of MTDs transmitting thep-th pilot,and we denotePpas the set of active MTDs that transmit thep-th pilot.His a row-sparse matrix with non-zeros rows indicating transmitted pilots.

Denotedk∈andsk∈as the transmitted symbols and the spreading sequence of thek-th MTD,respectively.Then the received data of them-th antenna at the BS is given as

III.RECEIVER ALGORITHM DESIGN

The mMIMO channel matrixHin Eq.(2) is a rowsparse matrix owing to the sporadic activity,and can be estimated by sparse recover algorithms,e.g.,OMPMMV[21].The index of non-zero rows in the recovered channel matrixindicates the set of detected active pilots.As the data matrixXin Eq.(4) and the channel matrixHin Eq.(2) have the same support,the recovered datacan be obtained via the least square(LS)method

Given the estimated channel,the transmitted datadpcorresponding to thep-th pilot can be recovered by

If the recovered data passes the cyclic redundancy check (CRC),it suggests the AUD and channel estimation are successful for the MTD transmitting thepth pilot.If MTDs in different clusters select the same pilot,the recovered channel is the superposition of all these MTD’s channel.In this case,the recovered data is not likely to pass the CRC.

To differentiate active MTDs of different clusters who transmitting the same pilot,we propose a dictionary learning assisted AUD method.Dictionary learning is a highly effective approach for extracting crucial features of the signals from a training dataset,particularly when the signals have sparse representations.Previous researches have proved its effectiveness when applied to classification tasks [22–24].Concretely,we could learn a cluster-specific dictionary,where the channel of MTDs in different clusters could be represented by different sub-dictionaries,and its representation possesses more prominent block sparse characteristics.To improve the accuracy of classification,it is essential to minimize similarities between the atoms of different sub-dictionaries,which makes it easier to distinguish MTDs from different clusters.

3.1 Dictionary Learning Assisted AUD

We consider to represent the active MTDs’ channel with a learned cluster-specific dictionaryD=[D1,D2,...,DC]∈CM×G,whereCdenotes the number of clusters,Gdenotes the number of atoms in the dictionary,andDi∈CM×g(i=1,2,...,C) denotes thei-th sub-dictionary corresponding to theith cluster,withg=G/Cdenoting the number of dictionary atoms in the sub-dictionary.Letbe the training data set,wherecontainsNsdifferent channels of MTDs in thei-th cluster.Mathematically,we can express,whereis the coefficient matrix of thei-th cluster corresponding to thej-th sub-dictionary.To differentiate the MTDs in different clusters,we would likeDito capture the features of channels for thei-th cluster,so thatcontains non-zero elements.A similar approach of learning sub-dictionaries for image classification is investigated in[24].Now,we can formulate the overall dictionary learning problem as follows

where‖·‖Fdenotes the Frobenius norm,D−i=[D1,...,Di−1,Di+1,...,DC]∈CM×(C−1)gdenotes the submatrix by removingDifromD.I∈Rp×pis an identity matrix.The termandare proposed to improve the irrelevance of atoms within one sub-dictionary and reduce the similarity between different sub-dictionaries,respectively.Similar to [24],λ1=＞0 andλ2=＞0 are the regularization coefficients for the self-incoherent term and cross-incoherent term,respectively.Ns,Candgdenote the number of training samples in one cluster,the number of clusters allowed to access in a frame,and the number of atoms in a subdictionary.η1＞0 andη2=2Cη1＞0 are adjustable parameters.We constrain dictionary atoms with normalized energy to avoid trivial solutions.

Since the objective function is not convex,we alternatively update the sparse coefficient of each cluster and the corresponding sub-dictionary with other variables fixed.First,we fixedDito update the sparse coefficient.Owing to the limited scattering,spatial channel in the MIMO system can be represented sparsely under the discrete fourier transform (DFT)[16].Thus,we initialize the dictionaryDas the redundant DFT matrix obtained by interpolation.Then,the optimization problem for updating sparse coefficients becomes

which is a least squares(LS)problem.can be updated with the closed-form expression

Given the sparse coefficient,the optimization problem with respect to thei-th sub-dictionary becomes

which can be solved using the gradient descent algorithm.We choose the step size following the Armijo rule.

By iteratively updating the dictionary and sparse coefficients until the reconstruction error no longer decreases,we obtain the learned cluster-specific dictionary.The learned dictionary is then used to identify the clusters of active MTDs.Firstly,according to the detected active pilot setand the estimated channel matrix,the recovered data symbols is given in Eq.(6).With the assistant of data recovery,the user detection problem can be formulated as

3.2 PD-NOMA Based Data Recovery

For MTDs selecting the same pilot,the BS is unable to correctly recover their data due to their superimposed channel.As these conflicted MTDs could be identified by the proposed CSDL-BOMP,the BS broadcasts information to inform the conflicted MTDs to retransmit their pilot on orthogonal resources for channel estimation.Then,conflicted MTDs resend their data on non-orthogonal resources via PD-NOMA,which can improve the spectrum efficiency of data transmission.The complete process of massive access and data transmission is shown in Figure 2.

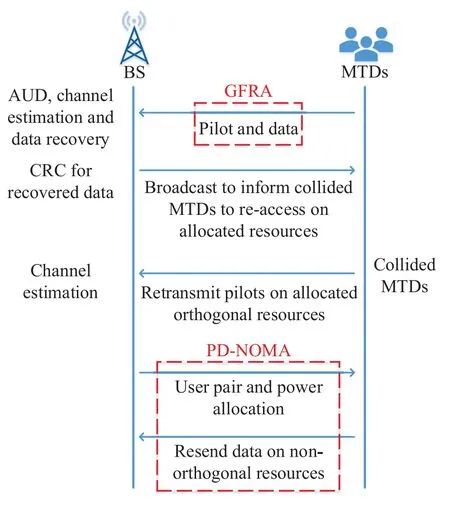
Figure 2. The complete process of massive access and data transmission.

The basic idea of PD-NOMA is to differentiate users through different power levels [26].In uplink PDNOMA,users in the cell are divided into several user groups,each usually containing 2～3 users.The BS allocates orthogonal resources to different user groups,while users in one group share the same resource.After receiving the superimposed user signal,the BS performs SIC to recover data.In this paper,before conflicting MTDs resend their data,the BS informs the detected active MTDs to resend orthogonal pilots to estimate their channel.After obtaining the channel state information (CSI),the BS pairs MTDs with the far near pairing method[27]and allocates different power to MTDs of the same pair.Then,MTDs assigned to the same group resend data according to the specified power.

Take a group of two MTDs as an example.The data symbols resent by MTD 1 and MTD 2 are denoted asd1∈andd2∈,respectively.The transmit power of MTD 1 and MTD 2 arep1andp2.Then,the received signalY∈at the BS is

whereh1∈CMandh2∈CMare channel coefficient vectors of MTD 1 and MTD 2,respectively.Without loss of generality,we assume thath1andh2are accurate,i.e.,channel estimation is perfect.Ndenotes the additive white Gaussian noise.After the BS receives the superimposed signal,SIC is applied for multi-user detection.Due to the fact that users with better channel conditions have stronger signal to noise ratios(SNRs),users with better channel conditions are usually decoded first.Here,we assume the channel condition of MTD 1 is better.Then,treating the interference from MTD 2 as noise,the BS will first decode the symbol of MTD 1 utilizing the LS method

After successfully decoding the symbol of MTD 1,the BS removes its interference from the received signalY,as the channel of MTD 1 is known to the BS.Then the signal of MTD 2 can be decoded through the LS method

IV.SIMULATION RESULTS

In this section,we investigate the performance of the proposed cluster-based CS massive access scheme with CSDL-BOMP for AUD and PD-NOMA for data re-transmission.The accuracy of pilot detection is defined as

whereManddenote the set of active pilot and detected active pilot,respectively.card(.) is the Cardinality of the set.The successful AUD ratioµuseris defined as

whereKanddenote the set of active MTDs and the set of detected active MTDs,respectively.Although the data recovery is conducted in both activity detection phase and data re-transmission phase,we use the user detection ratio to evaluate the performance in the first phase,while consider the data recovery ratio in the re-transmission to evaluate the performance of the second phase.The successful data recovery ratioµdatais defined as

withQandNredenoting the set of re-transmitted MTDs whose data is correctly recovered and the number of re-transmitted MTDs,respectively.For competitor methods in AUD,we choose the vector approximate message passing (VAMP) [15],sparse Bayesian learning (SBL) with angular domain enhancement (SBL-ADE) [16],and generalized MMVAMP (GMMV-AMP) [19] for comparison.For resolving collisions,we consider the contention-based method re-access method for comparison against the use of PD-NOMA.

In the experiments,we considerN=2000 stationary MTDs equipped with one antenna are randomly distributed in the cell,andNf=21 fixed FSCs are uniformly placed in the cell with the radius of 900 meters.Each channel response between the BS and the MTD consists of AOAs from 3 FSCs closest to the MTD and one AOA from a device location-related scattering.MTDs are separated into 2C=16 clusters according to their angular information.MTDs inC=8 non-adjacent clusters are allowed to access in one frame.To learn the cluster-specific dictionary,we generate a dataset containingNs=1000 channel responses per cluster and set the number of atoms in a sub-dictionarygto 8.As for the regularization coefficients for the self-incoherent term and crossincoherent term,we setη2andη1to 0.1 and 0.1/16,respectively.A common pilot pool withNp=125 andLp=64 is reused between clusters.The length of the spreading sequence isLd=18.The data is coded by using concatenated code,where the outer layer is a Reed-Solomom(RS)code with parameters(6,4)and the inner layer is a convolutional code with parameters(2,1,6).The modulation type is QPSK.Moreover,the numerical results are averaged over 300 trials.

First,we conducted an experiment to demonstrate the performance gain brought by cluster-based scheme.The comparison is non-cluster based scheme,i.e.,not separating MTDs and assigning a unique pilot to all potential MTDs.Figure 3 shows the performance of active pilot detection under a varying numbers of active MTDs.The cluster based scheme outperforms the non-cluster based scheme,as it reduces the number of needed pilot,leading to reduced interpilot interference.

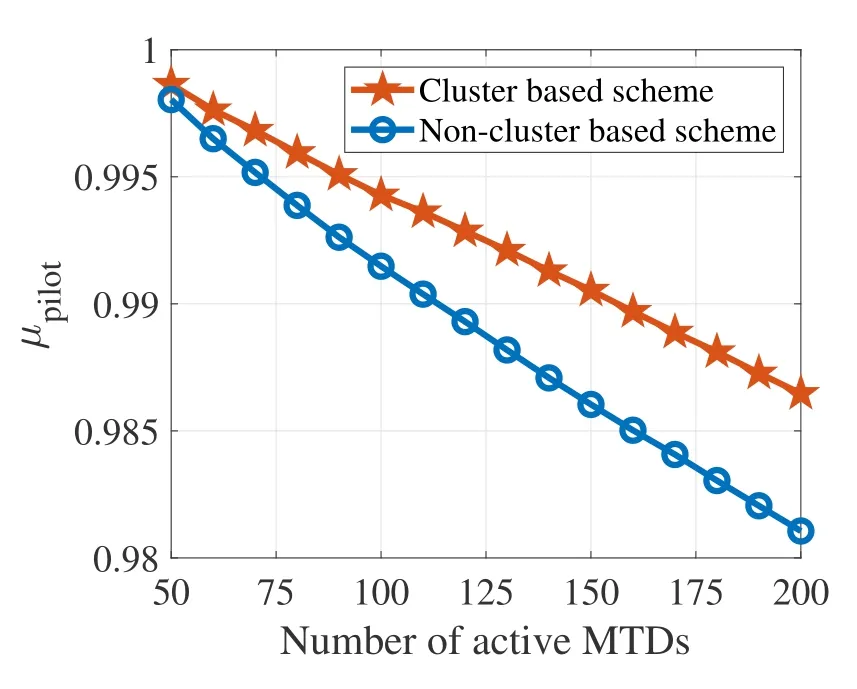
Figure 3.Active pilot detection performance with a varying number of active MTDs.

Figure 4 and Figure 5 show the performance of AUD under various SNRs and number of active users.The proposed method outperforms other competitors for all cases.The proposed method exploits both the the spatial channel features learned by dictionary learning and the non-orthogonal pilots to distinguish MTDs,which results in higher capability in AUD.It is worth noting that the dictionary learning is done in an offline manner using some training dataset collected from the cell.The CSDL-BOMP algorithm only uses the learned cluster-specific dictionary for AUD,which has a relatively low computational complexity.In our simulation platform,we observe that the computing time of the proposed method is only one-third of the SBLADE.

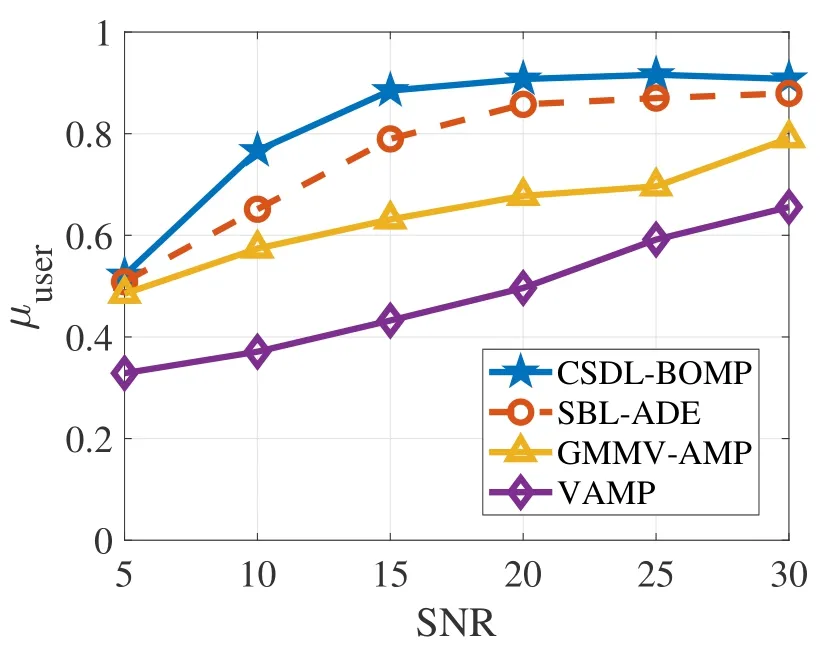
Figure 4. AUD performance under a varying SNRs.

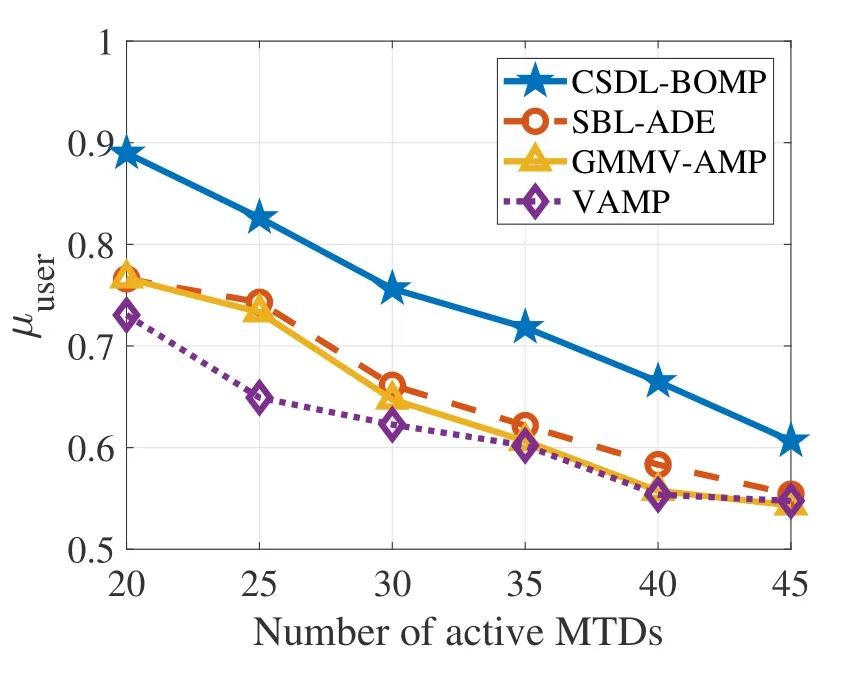
Figure 5. AUD performance with a varying number of active MTDs.

Figure 6 shows the performance of data recovery under various SNRs.Consistent with the results of AUD,the proposed method also shows superior performance in data recovery.A part of the gain comes from the improved AUD accuracy,as active MTDs of different clusters can be identified even they transmit the same pilot,and these MTDs’ data would be resolved by PD-NOMA during the re-transmission phase.For the SNR of 5 dB,the successful data recover ratio of the propose method reaches over 95%,while the other compared can only achieve about 78 −86%.

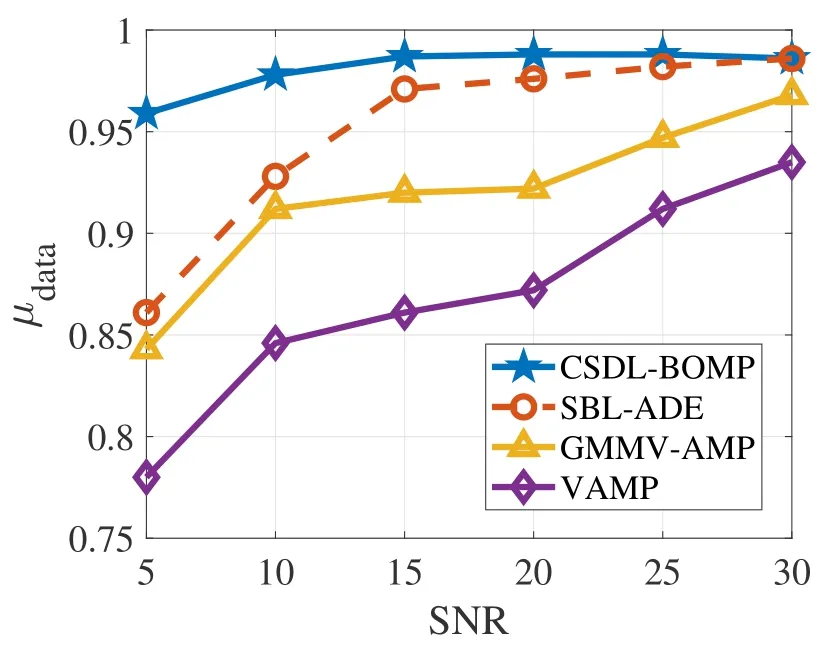
Figure 6. Data recovery performance under a varying SNRs in the data re-transmission phase.

Figure 7 shows the performance of data recovery under a varying number of active users.Under the experimental settings,the successful data recovery ratio keeps at a high level with the increasing number of active MTDs,while the performance of other methods degrades severely.This result is rationale.With more MTDs activated,the number of conflicted MTDs from different clusters,who select the same pilot,tends to increase.The proposed method can identify MTDs from different cluster and resolve collisions via retransmission with PD-NOMA,while the other methods cannot differentiate these MTDs and the performance of contention based re-transmission degrades with the increasing number of involved MTDs.

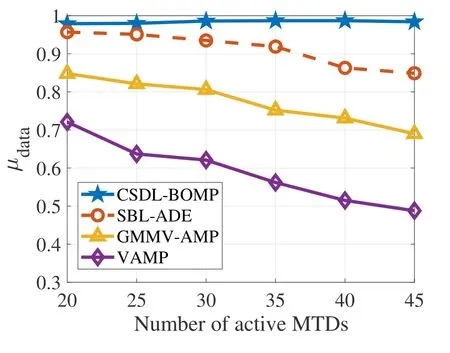
Figure 7. Data recovery performance with a varying number of active MTDs in the data re-transmission phase.

ACKNOWLEDGEMENT

This research was supported by Natural Science Foundation of China (62122012,62221001),the Beijing Natural Science Foundation(L202019,L211012),the Fundamental Research Funds for the Central Universities(2022JBQY004).

V.CONCLUSION

In this paper,we proposed a new massive access method for mMIMO systems,which separates MTDs into clusters and the same pilot pool could be reused among clusters.A cluster-specific dictionary can be learned form the historical channel dataset of the cell,and used to differentiate active MTDs of different clusters.For detected active MTDs whose data recovery fails,we utilized PD-NOMA with SIC to recover the re-transmitted data.Numerical results reveal that the proposed method has superior performance in AUD and data recovery against the existing methods designed for mMIMO systems.