A Joint Activity and Data Detection Scheme for Asynchronous Grant-Free Rateless Multiple Access

Wei Zhang,Xiaofeng Zhong,Shidong Zhou

Department of Electronic Engineering,Tsinghua University,Beijing 100084,China

Abstract: This paper considers the frameasynchronous grant-free rateless multiple access(FAGF-RMA) scenario,where users can initiate access at any symbol time,using shared channel resources to transmit data to the base station.Rateless coding is introduced to enhance the reliability of the system.Previous literature has shown that FA-GFRMA can achieve lower access delay than framesynchronous grant-free rateless multiple access (FSGF-RMA),with extreme reliability enabled by rateless coding.To support FA-GF-RMA in more practical scenarios,a joint activity and data detection (JADD)scheme is proposed.Exploiting the feature of sporadic traffic,approximate message passing (AMP) is exploited for transmission signal matrix estimation.Then,to determine the packet start points,a maximum posterior probability (MAP) estimation problem is solved based on the recovered transmitted signals,leveraging the intrinsic power pattern in the codeword.An iterative power-pattern-aided AMP algorithm is devised to enhance the estimation performance of AMP.Simulation results verify that the proposed solution achieves a delay performance that is comparable to the performance limit of FA-GF-RMA.

Keywords: asynchronous grant-free;JADD;rateless codes

I.INTRODUCTION

1.1 Backgrounds and Motivations

The proliferation of connected devices in the Internet of Things(IoT)[1]has given rise to numerous emerging applications of massive Machine Type Communications (mMTC) [2].In the era of the Internet of Things,wireless networks will provide differentiated services[3],including wide coverage,large-scale connectivity,high reliability,low latency,and high data rates for a vast number of devices.In the context of mMTC,data traffic exhibits characteristics such as a high proportion of uplink data,and bursty short packets [4].These features drive the need for an efficient random access scheme to address various service requirements,including large-scale access,low power usage,and Ultra-Reliable and Low-Latency Communications(URLLC)[5].

Conventional grant-based access procedure,adopted in Long Term Evolution-Advanced (LTE-A)[6]and the fifth-Generation New Radio(5G NR)[7],requires a four-step handshaking protocol,through which orthogonal radio resources are allocated to different users for uplink transmission.However,such protocol is inefficient in mMTC scenario,since the payload size may be much smaller than the signaling overhead.Moreover,it is hard to support massive device connectivity due to the frequent preamble collision[8].

To support URLLC and mMTC,grant-free access has been proposed and extensively discussed in both industry and academia.In this approach,the traditional grant request before uplink transmission is omitted to reduce control signaling overhead and access latency[9].

However,due to the lack of scheduling coordination,grant-free access may encounter serious collision problems where multiple users simultaneously use the same channel resources.To solve this problem,advanced receivers in Non-Orthogonal Multiple Access(NOMA)can recover multiple user data streams from interfered signals [10,11].In the context of NOMA,grant-free access faces a variable number of interfering users,leading to more dynamic channel conditions [12].To enhance reliability,conventional link adaptation methods select a fixed-rate code based on channel state information (CSI),involving feedback that results in additional waiting delays [13].In contrast,rateless coding offers an efficient,flexible alternative,which dynamically sets the code rate during transmission,adapting to CSI changes on the fly[14].Rateless coding involves the continuous generation of encoded symbols by the sender,without waiting for feedback.The receiver decodes the message successfully once it collects a sufficiently long codeword [15].Common rateless codes for additive white Gaussian noise(AWGN)channels include Analog Fountain Codes(AFC)[16]and Spinal codes[17].Notably,recent research on short packet AFC[18–20]has unveiled AFC’s potential to achieve latencies comparable to the Polyanskiy-Poor and Verdu(PPV)normal approximation bound [21],indicating AFC as a promising solution for URLLC.In this paper,we term grant-free access with rateless codes as grant-free rateless multiple access(GF-RMA).

Existing research on grant-free access typically assumes frame-synchronous transmission,restricting users to start access only at the beginning of a transmission period or frame,leading to potential waiting delays.In frame-synchronous grant-free rateless multiple access (FS-GF-RMA),without strict delay constraints but zero tolerance for packet loss,the transmission period continues until all active users are successfully decoded.If there is a high number of active users or a user experiences poor channel conditions,the transmission period could extend significantly.Consequently,a substantial group of users with new packets may initiate their access in unison in the following transmission period,potentially further lengthening it.As demonstrated in[22],an unstable condition arises in the FS-GF-RMA system when the packet arrival rate is excessively high.In such cases,the average number of active users during the transmission period surpasses that of the previous period,and the average transmission delay increases over time to infinity.

To address this,frame-asynchronous grant-free rateless multiple access (FA-GF-RMA) is proposed in[23],which allows users to initiate access at any time,thus eliminating waiting delays.The authors in [24]show that FA-GF-RMA is stable and achieves significantly lower delays than FS-GF-RMA,especially in low signal-to-noise ratio (SNR) or high packet arrival rate scenarios,indicating that FA-GF-RMA is a promising approach for achieving URLLC in powerconstrained or high-traffic-load conditions.

However,the delay comparison in[24]is conducted under ideal conditions including perfect knowledge of activity and channel state,as well as capacityachieving codes.Whether the delay advantages of FAGF-RMA persist in more practical conditions needs to be verified.Furthermore,to fulfill the advantages of FA-GF-RMA,it is necessary to address the potential challenges in its practical implementation,including activity detection,transmission starting point estimation,channel estimation,and demodulation.

1.2 Related Works

In scenarios with low mobility,such as indoor environments or monitoring with fixed sensors,the channel coherence time greatly exceeds the data transmission time.In such cases,it is feasible to assume that the receiver has prior knowledge of CSI for each potential device,which can be obtained through an initial channel estimation process.The receiver’s task is to perform joint activity and data detection(JADD)over an extended coherent period.In this work,we consider the case of perfect CSI at the receiver.

Due to the sporadic feature of traffic in mMTC,JADD is often cast as a sparse signal recovery problem,which can be efficiently solved by compressive sensing (CS) techniques.A great number of works have studied CS-based JADD for synchronous grantfree access.

In [25],the temporal correlation of the active user sets between adjacent time slots is exploited to realize JADD in several continuous time slots through the Orthogonal Matching Pursuit (OMP) algorithm.While in[26],a parameter evaluating the quality of the previous active user set is introduced,which is used as prior information to aid the subspace pursuit(SP)algorithm for solving JADD.The greedy-based algorithms fail to utilize the prior distribution of the transmitted signals,and the matrix inversions incorporated in them cause high computational complexity when the system scale is large.Recently,the CS techniques under the framework of Bayesian inference,such as Approximate Message Passing (AMP) [27],Orthogonal Approximate Message Passing(OAMP) [28],Expectation propagation (EP) [29] and so on,have gained great attention in JADD due to their flexibility and accuracy.In [30],an AMP-based detection scheme is proposed with the hyper-parameters of device activity learned through the Expectation Maximization (EM)algorithm.The authors in [31] develop an OAMPbased algorithm to solve the multiple measurement vectors (MMV) problem,which devises a structurelearning module to leverage the structured sparsity of uplink signals among multiple time slots.

Some research works have explored framesynchronous access without uplink synchronization.Assuming that timing offsets are integer multiples of the symbol interval,[32] proposes a model-driven deep learning approach,which is termed Learned Approximate Message Passing Algorithm (LAMP)to address issues concerning activity detection,time offset estimation,and channel estimation.The authors in [33] consider scenarios with continuous-valued timing offsets where inter-symbol-interference exists.By assuming the knowledge of the delay profile at the receiver,they devise a sparse Bayesian learning algorithm based on the message-passing framework for activity detection and channel estimation,which allows the receiver to harness timing offsets among users for improved multi-user interference suppression.

It’s worth noting that in frame-synchronous access without uplink synchronization,the starting points of user data packets are also misaligned but within the maximum propagation delay of the cell.While in the frame-asynchronous grant-free access considered in this paper,users can initiate access at any time,and the deviations between the starting points of user data packets may be comparable to the packet length.

Some researchers have investigated the blind detection problem of frame-asynchronous grant-free access.In[34],the sliding-window detection framework is employed,and by exploiting the sparsity structure embedded in the signal matrix in an observation window,a blind detection algorithm termed turbo bilinear generalized approximate message passing(Turbo-BiG-AMP) is proposed to recover the channel,the transmission start points of active users,and the user data in a single phase.In [35],the Turbo-BiG-AMP algorithm is further extended to asynchronous grantfree access without uplink synchronization.However,both studies assume the receiver knows the number of active users in an observation window,which might limit their applicability in grant-free access scenarios where the number is often unknown in advance.

The above-mentioned works all address receiver design issues for grant-free access with a fixed data rate.As for frame-asynchronous grant-free access with rateless codes,the authors in[36]have devised a novel joint user activity detection and channel estimation scheme.However,the delay performance of FAGF-RMA with practical rateless codes is not demonstrated in[36].In this paper,we focus on the joint detection of user activities and data with the knowledge of CSI at the receiver and evaluate the delay performances of FA-GF-RMA employing AFC.

1.3 Our Contribution

This paper investigates the JADD problem for FA-GFRMA.To the best of our knowledge,this is the first attempt to address the JADD problem in the FA-GFRMA system.To this end,we utilized the AMP-based JADD algorithm to recover the active user set and their transmitted signals,and then estimate the transmission start points by exploiting the intrinsic power mode.The proposed JADD solution can be used in FA-GF-RMA with any specific rateless code.Particularly,we use AFC as an example to verify the delay performances of the proposed JADD solution.

The rest of the paper is organized as follows.Section II describes the system model of FA-GF-RMA and briefly introduces the AFC.Section III formulates the JADD problem in FA-GF-RMA.In Section IV,we present the proposed solution.Simulation results are given in Section V to demonstrate the effectiveness of the proposed algorithm.Finally,conclusions are drawn in Section VI.

Notations: We use bold upper and lower case letters for matrices and column vectors,respectively.For a matrixS,we usesi,j,sj,Sk,:andSk,a:bto denote the entry in thei-th row and thej-th column,thej-th column,thek-th row and the row vector composed of itsa-th tob-th elements in thek-th row,respectively.IMdenotes the identity matrix of sizeM×M.CN(x;µ,Γ)denotes the complex Gaussian distribution of a random vectorxwith meanµand covariance matrixΓ.R+and C represent the positive real number and complex number set,respectively.

II.SYSTEM MODEL

We consider a typical scenario of uplink grant-free access.A base station equipped withGantennas servesKInternet of Things (IoT) devices.Assume that all users have achieved uplink synchronization with the base station.Each user generates a fixed-size data packet stream according to a Poisson process with an arrival rate ofλpackets per symbol.In FA-GF-RMA,users are allowed to initiate data packet transmission at the beginning of any symbol interval.

When a user’s data packet arrives,it is first encoded via AFC to generate a potentially infinite-length codeword.Then the coded symbols are transmitted successively until an acknowledgment (ACK) is received from the base station or the maximum transmission time is reached1.If an ACK is not received before reaching the maximum transmission timeL,the packet is considered an outage.

Letτk,jdenote the time at which userkstarts transmitting itsj-th data packet,andζk,jdenote the time at which userkstops transmitting itsj-th data packet.As shown in Figure 1,the first packet of user 1 starts transmission atτ1,1and receives an ACK atζ1,1,resulting in an early termination of the transmission.While the first packet of user 2 starts transmission atτ2,1but continues until the maximum codeword length is reached without receiving an ACK,therefore,it is outaged.

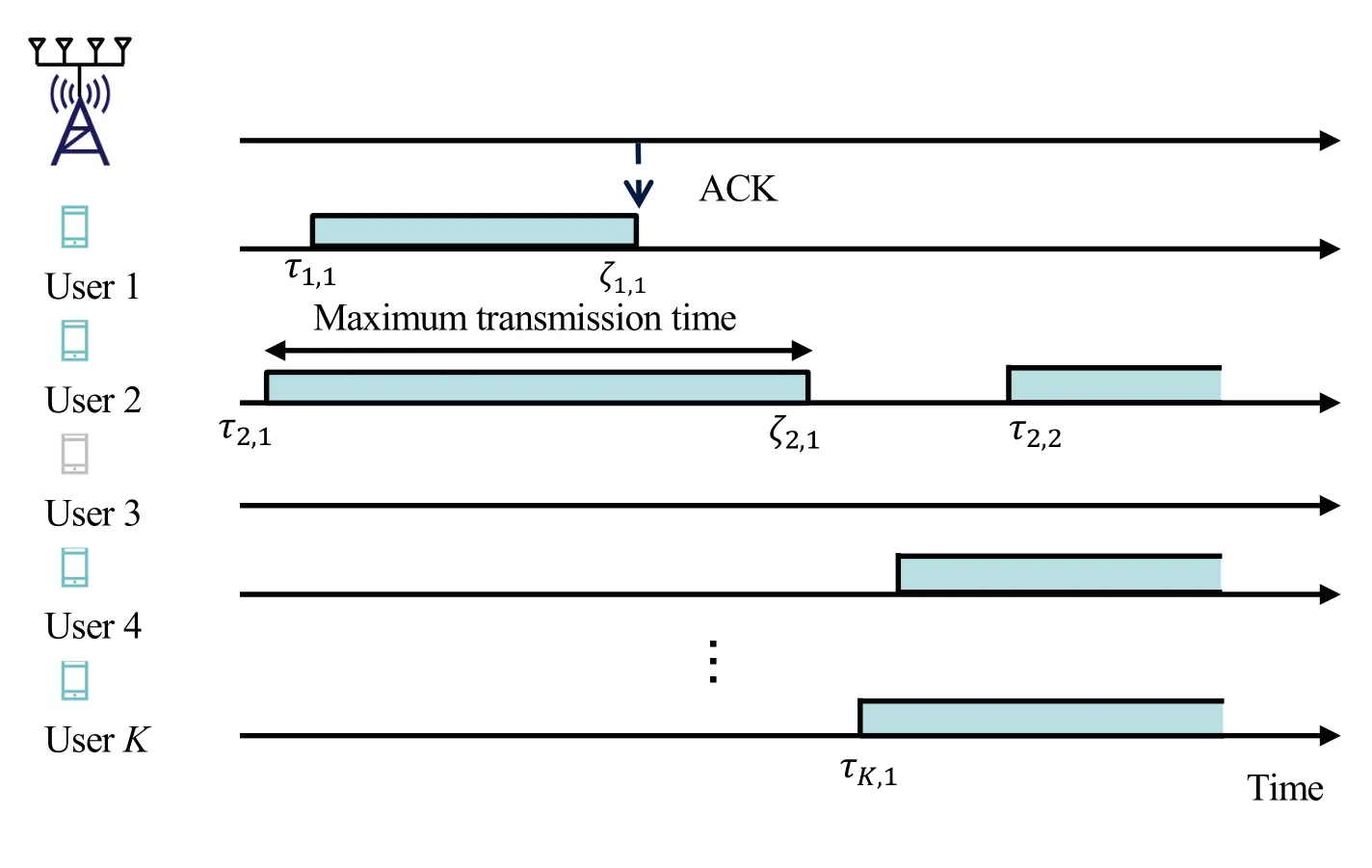
Figure 1. The sporadic and asynchronous packet transmissions in FA-GF-RMA.

2.1 Analog Fountain Codes

The analog fountain code (AFC) is a representative rateless code,initially introduced in[16].In this work,we choose AFC as a specific rateless coding scheme to exemplify the demodulation and decoding challenges of FA-GF-RMA,considering the AFC’s significant promise in achieving URLLC.For the convenience of our readers,we first provide a brief overview of AFC’s encoding and decoding processes.

Before applying AFC encoding,the entire data block ofNbinformation bits undergo binary phase shift keying (BPSK) modulation to obtainNbinformation symbolsb≜.

The encoding process of AFC is represented by an infinite-row generator matrixG,featuring a constant number of columns denoted asNb.Each row of matrixGis inherently sparse,with its non-zero elements uniformly drawn from a pre-defined setWof real-number weights,evenly distributed within the row.The number of non-zero elements,denoted asdifor thei-th row,is determined by a pre-defined degree distribution function Ω(x)=.Denote the index of thej-th non-zero element in thei-th row as,and the corresponding index of weight coefficient as,then thei-th real-domain AFC coded symbolis generated as

Regarding the coded symbols as factor nodes and information symbols as variable nodes,the AFC encoding process can also be described by a bipartite graph,as shown in Figure 2.Assuming the weight set is energy-normalized,i.e.,=1,the average power of thei-th AFC-coded symboldi.

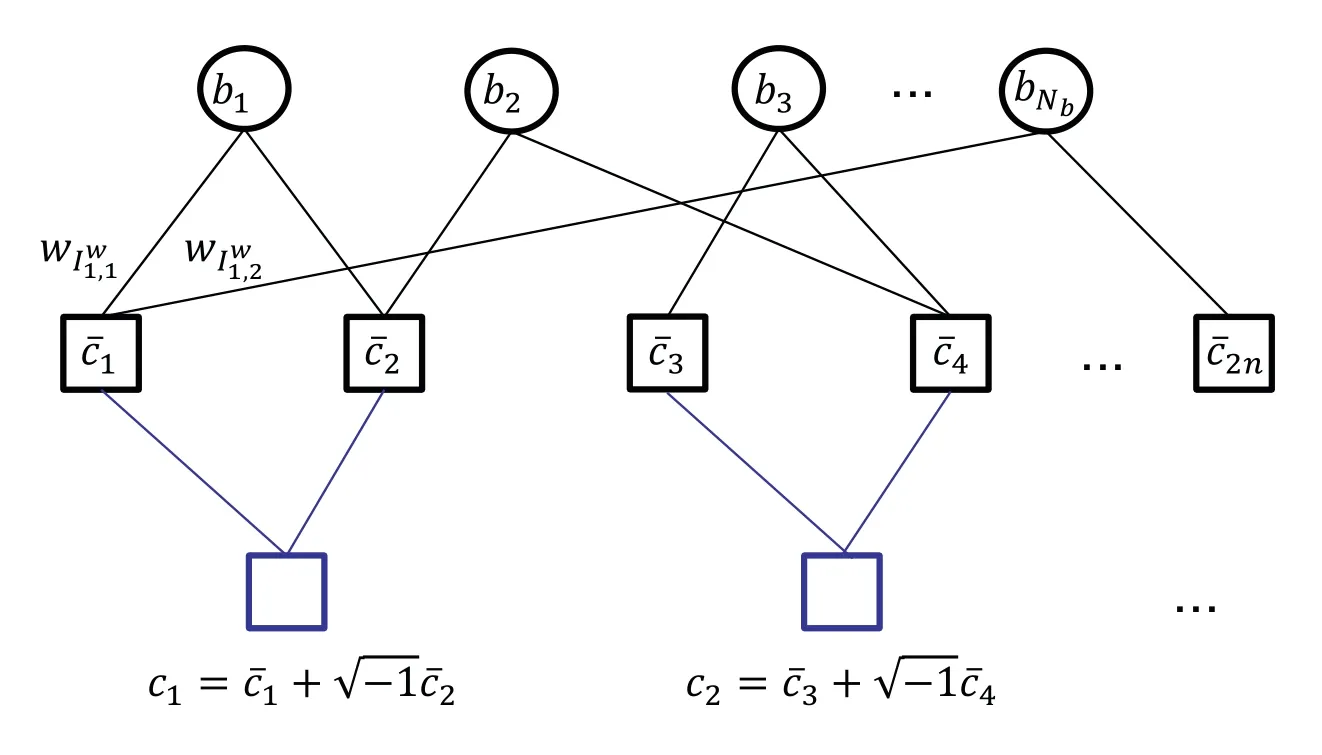
Figure 2. The encoding bipartite graph of AFC and the modulation of real-domain coded symbols.

To fully utilize the constellation plane,each two consecutive real-domain coded symbols compose one complex-domain symbol.Specifically,define a modulator Φ,that transforms the real-domain coded symbols into complex-domain symbols:

Theoretically,the AFC encoder can generate an infinite number of coded symbols.Practically,considering the maximum transmission timeL,each packet may be encoded into at most 2Lreal-domain coded symbols.The generator matrixGis of size 2L×Nb.

Upon receivingn0(n0＜2L) real-domain AFC coded symbols,the receiver attempts to decode.If the decoding fails,the receiver continues to collect additionalδsymbols and reruns the decoder.This process continues until successful decoding or the received codeword reaches the maximum length.At the stage of receivingnreal-domain coded symbols,the receiver constructs a sub-graph based on the 1st to then-th row ofGand then runs the belief propagation (BP) decoding algorithm on the graph to obtain the log-likelihood ratios (LLRs) for each information symbol [37].To mitigate error floor,in practice,a fixed-rate precoder may be concatenated to the AFC encoder,e.g.a low-density parity check precoder.

In a multi-user access scenario,each userkis allocated a unique random seed to construct the generator matrixGk.The assignment of these random seeds is known to the receiver,enabling the retrieval of the generator matrices on the receiver’s side for decoding.

2.2 Signal Model

Lethkdenote the channel vector of userk,following a complex Gaussian distributionCN(0,βkIG),whereβkrepresents the path loss and large-scale fading andGis the number of antennas.

Letck,j=[ck,j(1),...,ck,j(L)]T∈CL×1represent the AFC codeword of thej-th data packet of userk,andsk,trepresents the signal transmitted by userkat timet.Then

wherel=t−τk,j+1 andpk,lis the power gain factor of thel-th coded symbol of userk’s packets.The average transmission powerof thel-th AFC-coded symbol of userkis given by

wheredk,lis the degree of thel-th real-domain AFCcoded symbol of userk.

At thet-th symbol instant,the received signal at the base station can be expressed as

whereH=[h1,...,hK] represents the matrix composed of channel vectors of forKpotential users,Gis the number of receive antennas,st=[s1,t,...,sK,t]Trepresents the vector of transmitted signals fromKusers at timet,andntrepresents the Gaussian white noise distributed asCN（0,σ2IG）.

This paper assumes that the channel matrixHis known at the receiver.To accomplish decoding,the receiver needs to recover the starting points of each data packet{τk,j|∀k,j}and the data packet codewords {ck,j|∀k,j}based on the received signals {yt|t≥0}.

2.3 The Sliding-Window Framework

Given user-initiated access at arbitrary times,we employ a sliding-window framework for packet detection,with window length denoted asWand the sliding step as Δ.While a largerWenhances detection performance through extended observations,it concurrently increases complexity.Given that the maximum codeword length of each packet isL,it is judicious to setW=L.This configuration allows the receiver to observe the maximum-length codeword at a minimal increase in computational complexity.

Assuming the current time ist,then the sliding window spans fromt−L+1 tot.Within this window,the signal model is denoted as

whereS(t)=[st−L+1,...,st]∈CK×L,andN(t)=[nt−L+1,...,nt]∈CG×L.

Active users,in this context,are defined as those who transmit signals within the window.As depicted in Figure 3,there are three distinct types of packets transmitted by active users within the sliding window:

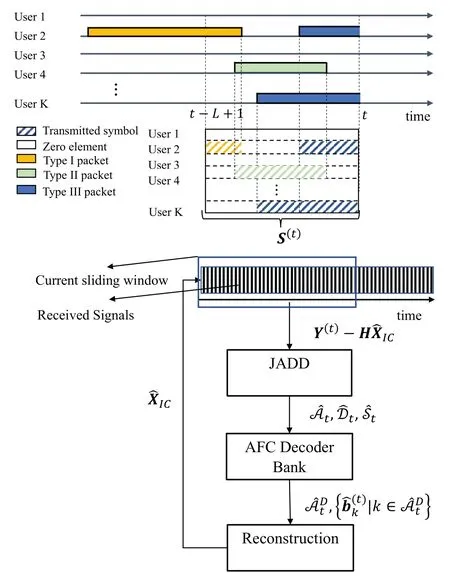
Figure 3. Illustration of the sliding-window framework and the receiver structure,where S(t) represents the transmitted signal matrix of the current window.

• Type I:packets that start transmission beforet−L+1 and stop within the window,possibly due to successful decoding or an outage event.

• Type II:packets that initiate and terminate transmission during the window,signifying successful decoding.

• Type III:packets that start transmission within the window but remain undecoded at this stage.

In each window,it is only necessary to detect type III packets.LetAt,Dt,andStrepresent,respectively,the sets of active users,the starting points,and the transmitted signals corresponding to type III packets in thet-th window,which will be formulated in the next section.

As illustrated in Figure 3,the JADD module provides the estimation ofAt,DtandSt,denoted as.Subsequently,the decoder bank concurrently attempts to decode the packets of users inbased on the estimations of the transmitted codeword signals.Upon successful decoding of packets,the respective transmitted codeword signals can be accurately reconstructed,facilitating interference cancellation to improve the performance of the JADD module.The iteration between the JADD module and the decoder bank stops when no more packets can be decoded,at which point the window advances by a step of Δ.For clarity,the receiver structure is described in Algorithm 1.

III.FORMULATION OF THE JADD PROBLEM IN FA-GF-RMA

As mentioned in the previous section,the objective of JADD in FA-GF-RMA is to identify the users with an undecoded packet that initiates transmission within the sliding window,determine their transmission start times,and estimate their transmitted codeword signals.This section is dedicated to formulating the JADD problem in FA-GF-RMA.

Given that the transmitted signals from the decoded packets are effectively canceled,within a sliding window of lengthL(equal to the maximum transmission time),only the signals of the type III packets and type I packets are received.In other words,for each active user,a maximum of two undecoded packets from the same user can be observed within a given sliding window.The first packet is of type I and represents an outage,while the second is of type III and remains undecoded.

The above observation can be formulated as follows.Let the relative ending point of the type I packet and the relative starting point of the type III packet for userkin thet-th sliding window be denoted asand,respectively.We define the tupleas theactivity modeof userkin sliding windowt.For allkandt,∈M,whereMis defined as {(ζ,τ)|1≤ζ＜τ≤L}∪{(0,τ)|1≤τ≤L}∪{(ζ,L+1)|1≤ζ＜L}∪{(0,L+1)} and |M|=3L2/2−L/2.

For the convenience of description,we refer to(0,L+1) as the inactive mode and the others as active modes.And an integer∈{0,1,...,|M|−1} is used to denote the activity mode of userkin windowt.Then the original activity mode is retrieved via two pre-defined one-to-one mappingsfζandfτas.In particular,we setfζ(0)=0 andfτ(0)=L+1,indicating thatmk=0 represents the inactive mode.

With the above notations,the set of active users of type III packetsAt,the set of corresponding starting pointsDt,and the set of transmitted codeword signalsStare formulated as follows,

Consider an arbitrary window and drop the superscript (t) for simplicity,the signal model is rewritten as

In order to provide the estimations ofAt,DtandSt,it is necessary to recover the signal matrixSand the latent activity modesm=[m1,...,mK]Tbased on the observationsY.

The minimum mean square error(MMSE)estimator ofsk,lis the posterior mean,which can be expressed as

whereSk,ldenotes the collection of all elements inSexceptsk,l,and

The factorization ofp(Y|S)andp(S)in Eq.(12)is due to the assumption of AWGN and the independence across the users,respectively.

To provide the maximum a posteriori (MAP) estimation ofmk,the posterior distribution ofmkneeds to be evaluated,which is expressed as

wheremkdenotes the collection of all elements inmexceptmk,and

IV.THE PROPOSED JADD ALGORITHM

Both the MMSE and MAP estimators necessitate the evaluation of posterior distributions that involve intractable integrals.Therefore,in this section,we propose an approximate approach to obtain the MMSE and MAP estimations.

First,exploiting the clustered sparsity structure ofS,the approximate message passing with nearest neighbor sparsity pattern learning(AMP-NNSPL)algorithm is employed to obtain ˆSand identify active users.Then,a power-pattern-based maximum a posteriori (MAP) algorithm is introduced to estimatemkfor all detected active users,given by.Finally,we propose a novel iterative scheme that combines the AMP-NNSPL and power-pattern-based MAP algorithms to enhance estimation performance.

4.1 The AMP-NNSPL Algorithm

Because of the sporadic nature of MMTC,only a small fraction of potential users are active at any given time.Consequently,the columns ofSare sparse vectors.Therefore,the recovery of each column ofScan be conceptualized as a single measurement vector(SMV)problem in the field of compressed sensing,which can be efficiently addressed using the AMP algorithm.

Specifically,considering thel-th symbol time within the sliding window,the received signal at this moment can be represented as

whereHis the known channel matrix,andsl=[s1,l,...,sK,l]Tis the sparse vector to be estimated.

To characterize the sparsity ofsl,a flexible spike and slab prior distribution is adopted,i.e.,

wheref(sk,l) characterize the distribution of thel-th AFC-coded symbol of userk’s packets.In this work,we assume a Gaussian distribution for the AFC-coded symbols2.Therefore,in Eq.(16),for allkandl,f(sk,l)=CN（sk,l;0,ψ2）with the varianceψ2evaluated as.

At theq-th iteration,the AMP algorithm provides an estimation ofp(sk,l|yl)as

which can be interpreted as the posterior distribution ofsk,lgiven an observation,whereis the independent effective Gaussian noise with zero mean and variance.Given the a priori model in Eq.(16),the estimated posterior distribution is rearranged as

It is worth noting that the estimated posterior distribution is a Bernoulli Gaussian distribution,in whichcan be interpreted as the posterior probability ofsk,lbeing non-zero or belief indicator.

Assuming that the columns ofSare mutually independent,the posterior distributionp(sk,l|Y)=p(sk,l|yl).Then the posterior expectationand varianceat theq-th iteration are respectively given as

And the estimation ofsk,lis provided as.

Nevertheless,independently recoveringLcolumns ofSvia AMP does not leverage the inherent sparsity structure and may consequently result in unsatisfactory performance.As depicted in Figure 3,the nonall-zero rows ofSexhibit a clustered sparsity structure,where the non-zero elements are grouped into a block.Similar clustered sparsity structures have appeared in the previous literature [38,39],where the nearest neighbor sparsity pattern learning (NNSPL)technique is applied to the original AMP algorithm.The rationale behind NNSPL is thatsk,land its neighboring elements,such assk,l−1andsk,l+1,tend to be either simultaneously zero or non-zero.

In this paper,we adopt the AMP-NNSPL algorithm to accommodate the clustered sparsity structure exhibited in FA-GF-RMA.In Algorithm 2,Nl≜{l−1,l+1}represents the two neighbors of thel-th element andqmaxis the predefined number of iterations.

The AMP-NNSPL algorithm directly provides the estimation of transmitted signals.To obtain,activity detection is required.A method of activity detection based on the belief indicators is developed in [39].For convenience of description,we define a symbol-level activity stateαk,las

and define a threshold functionr(x;ϵ),wherer(x;ϵ)=1 if|x|＞ϵand otherwiser(x;ϵ)=0.

The activity detection begins by making a threshold decision on symbol-level activity states,which employs

Subsequently,the user-level activity is is determined as

Then the active user set is estimated as.Note that the thresholdpthcan be considered the required proportion of active symbols to categorize a user as active.In general,a higherpthresults in a set that includes only users whose transmitted codewords are sufficiently lengthy,whereas loweringpthreduces the risk of miss detection but raises the false alarm rate.

However,activity detection can only identify whether a user is active but not able to distinguish among active modes.In the next sub-section,we develop a power-pattern-based activity mode estimation algorithm.

4.2 Power-Pattern-Based Activity Mode Estimation

As mentioned in the previous sub-section,the AMPNNSPL algorithm falls short in estimating the activity modemk,making it incapable of providing estimates for the starting points of type III packets.Despite its ability to produce belief indicators for symbol-level activity,they lack the required reliability to determine the starting point,as depicted in Figure 4.

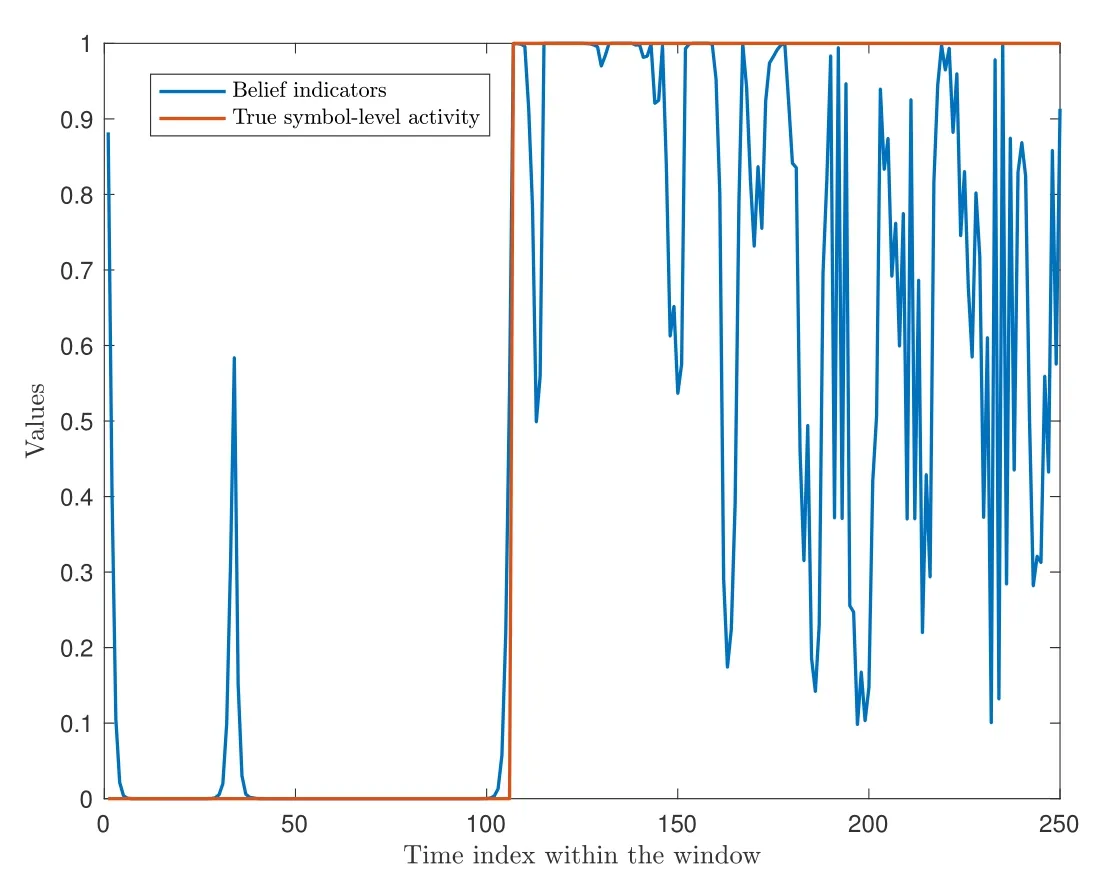
Figure 4. The typical per-symbol posterior probability curves of active users output by the AMP-SSL algorithm are shown with K=500,M=50,and λ=0.0002.

Moreover,in cases where a codeword begins with a zero symbol,which is possible with the AFC code,the related belief indicator typically approaches nearly zero.This situation will result in an erroneous identification of the packet’s starting point via the belief indicators,delayed by one symbol.

To address the activity mode estimation problem,we resort to the estimation of transmitted signals.From Eq.(4),it is evident that the transmission power of AFC-coded symbols fluctuates over time due to the variable degree or power gain factor.This power variation,referred to as the power pattern,can be harnessed.By purposefully designing the power mode to exhibit favorable auto-correlation properties,noticeable second-order statistical distinctions can emerge among the transmitted signals of packets starting at different time instances.These distinctions can subsequently be employed to distinguish the starting points of the packets.

Notice that given the activity modemk,the elements inSk,:are mutually independent.Therefore,p(Sk,:|mk)=∏l p(sk,l|mk),where

Herefk,l(·) denotes the distribution of thel-th transmitted AFC-coded symbol of userk’s packets.With the Gaussian assumption of AFC-coded symbols,fk,l(·)=CN(·;0,),whereis given by Eq.(4).

Therefore,given the activity modemk,the transmitted signals within a sliding window [sk,l,...,sk,L]can be regarded as a zero-mean,variance-varying discrete Gaussian process,where the conditional varianceofsk,lis given by

Now decompose the estimated signals as

where the estimation errorek,lis modeled as a Gaussian noise with distributionCN(0,).

Then the posterior probability ofmkgiven the estimated signalsis expressed as

and the estimated starting point is.

Note that the activity mode estimation is carried out on a per-user basis,which can be computationally intensive,especially when dealing with a large number of potential users.To reduce complexity,it is feasible to conduct the estimation solely for users within the set,which is obtained through the activity detection process.

4.3 The Proposed Power Pattern Aided AMP Algorithm

A straightforward approach for JADD in FA-GFRMA is to concatenate the power-pattern-based activity mode estimation module after the AMP-NNSPL algorithm.However,since prior information on power patterns is utilized during the activity mode estimation phase,it could be advantageous to iterate between these two steps to fully leverage the power patterns and enhance both algorithms’performance.

Notice that Eq.(27)provides a posterior distribution of the activity mode given the estimated signals.Based on the relation between the activity mode and the symbol-level activity states as shown in Eq.(21),it is feasible to derive a posterior distribution of the symbol-level activity stateαk,las

whereMl={m|∀m∈M,fτ(m)≤l or fζ(m)≥l}.

Intuitively,the activity mode estimation accuracy improves with the number of transmitted coded symbols in a window,as different modes exhibit greater distinctions in power patterns over a longer range of transmitted codewords.Consequently,the reliability of the posterior symbol-level active probabilityimproves with the codeword length.Therefore,the power-pattern information from longer-codeword users can be applied to the AMP-NNSPL algorithm by updating the corresponding symbol-level active probabilitiesγk,las,potentially enhancing the estimation quality of the signal of the shorter-codeword users.This process can be iteratively executed to fully leverage the power-pattern information from all active users in descending order of codeword length.

The above intuition is implemented in the proposed power-pattern-aided AMP(PP-AMP)algorithm 3,which can be summarized as the following 3 steps

• Step 1: Run the AMP-NNSPL to obtain the estimated signal matrixand the belief indicators.(Line 3)

• Step 2: Perform the active user detection with a decreasing thresholdpthuntil enough active users are detected.(Line 4-13)

• Step 3: Run the power-pattern-based activity mode estimation procedure for the detected active users and update their prior symbol-level active probabilities.(Line 15-21)

Notice that the thresholdpthdecreases frompINtop0with a steppδduring the iteration.A higherpINensures that users with sufficiently long codewords are initially detected.Asp0is increased,users with relatively short codewords are excluded from the iteration,as their power-pattern information might be unreliable and unhelpful.

4.4 Computational Complexity Analysis

The computational complexity of the algorithms is quantified in terms of the number of complex-valued scalar multiplications.In the AMP-NNSPL algorithm,each iteration requires approximately 7GKL+2GL+15KLmultiplications.In the power-pattern-based activity mode estimation,evaluating a posterior distribution of |M| values is necessary for each active user,with each probability value involving 3Lmultiplications,and therefore 3KaL|M|=multiplications are required in each iteration.HereKarepresents the number of active users,which is much less than the number of potential usersK.

Significant computational complexity arises from the large number of activity modesM,which scales on the order ofL2.In practice,given the infrequent occurrence of outage events,it is possible to work with a reduced set of activity modes that excludes those related to type I packets,i.e.,M={(0,τ)|1≤τ≤L+1}.In this case,the complexity of activity mode estimation is reduced to 3Ka(L2+L)per iteration.

V.SIMULATION RESULTS

In this section,Monte Carlo simulations are conducted to verify the performance of the proposed JADD algorithm in FA-GF-RMA.In the simulations,the number of users is set toK=500,and the packet size is fixed at 100 bits.Each user generates a data packet flow according to a Poisson process with an arrival rate ofλper symbol interval.The large-scale coefficients of all users are normalized,i.e.,βk=1.The signal-to-noise ratio (SNR) is defined as the ratio of average transmitting power to noise power.The information bits of user data packets are not pre-coded and are directly input to the AFC encoder after BPSK modulation.A fixed-degree AFC code with a degree of 8 and a weight set{1,2,3,4}is employed[20],and its energy is normalized3.For power pattern generation,the power gain factorpk,lin Eq.(3) is independently and uniformly sampled from the set{0.4,1.6}.The AFC code has a maximum length ofL=250,and AFC decoding is accomplished using the BP algorithm.The receiver attempts decoding whenever the window moves forward with a step size of Δ=2.Successful decoding is confirmed when the BPSK sequence of the data packet is fully restored.

First,we run simulations according to the signal model Eq.(10).In these simulations,to mimic the sparsity structure ofS,each user is activated with a probability ofKa/K,whereKaimplies the average number of active users.Each active user then selects a starting point drawn from either the range[131,250]with a probability of 0.8 or[51,130]with a probability of 0.2.For performance evaluation,we use the metrics of mean squared error (MSE),normalized mean squared error of codeword (NMSE-C),and starting point estimation error rate(SPER),which are defined respectively as

wherelrepresents the codeword length and I {·} is the indicator function.

Figure 5 presents a comparison of the MSE performance between the AMP-NNSPL algorithm and the proposed PP-AMP algorithm.The benchmark used for this comparison is the Oracle Linear Minimum Mean Squared Error (LMMSE) algorithm,which assumes knowledge of symbol-level activities and recovers the signal matrix column by column through LMMSE.The results clearly demonstrate that the proposed PP-AMP outperforms the original AMPNNSPL algorithm,closely approaching the performance of the Oracle LMMSE.The MSE reduction of PP-AMP concerning AMP-NNSPL becomes more significant as the number of antennas decreases or the average number of active users increases.This suggests that the proposed PP-AMP algorithm effectively leverages the sparsity structure,enabling support for more active users with fewer antennas.

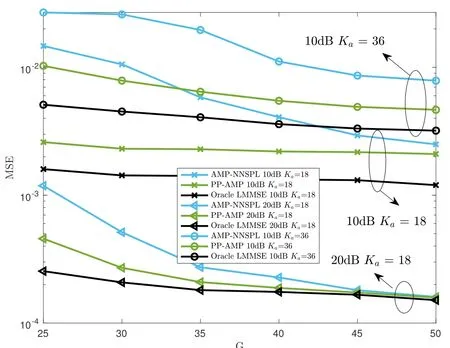
Figure 5. Comparison of MSE versus the number of antennas for the proposed PP-AMP and the state-of-art AMP-NNSPL algorithms.

Figure 6 and Figure 7 compare the NMSE-C and SPER performance for the various algorithms as a function of received codeword length.For the AMPNNSPL and Oracle LMMSE algorithms,the SPER curves are obtained by conducting the starting point estimation for the estimated signals.

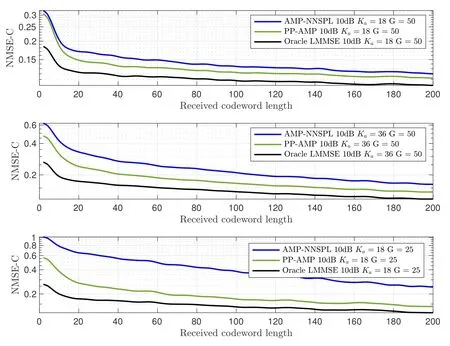
Figure 6. Comparison of NMSE-c versus the length of received codeword length l for the proposed PP-AMP and the stateof-art AMP-NNSPL algorithms.

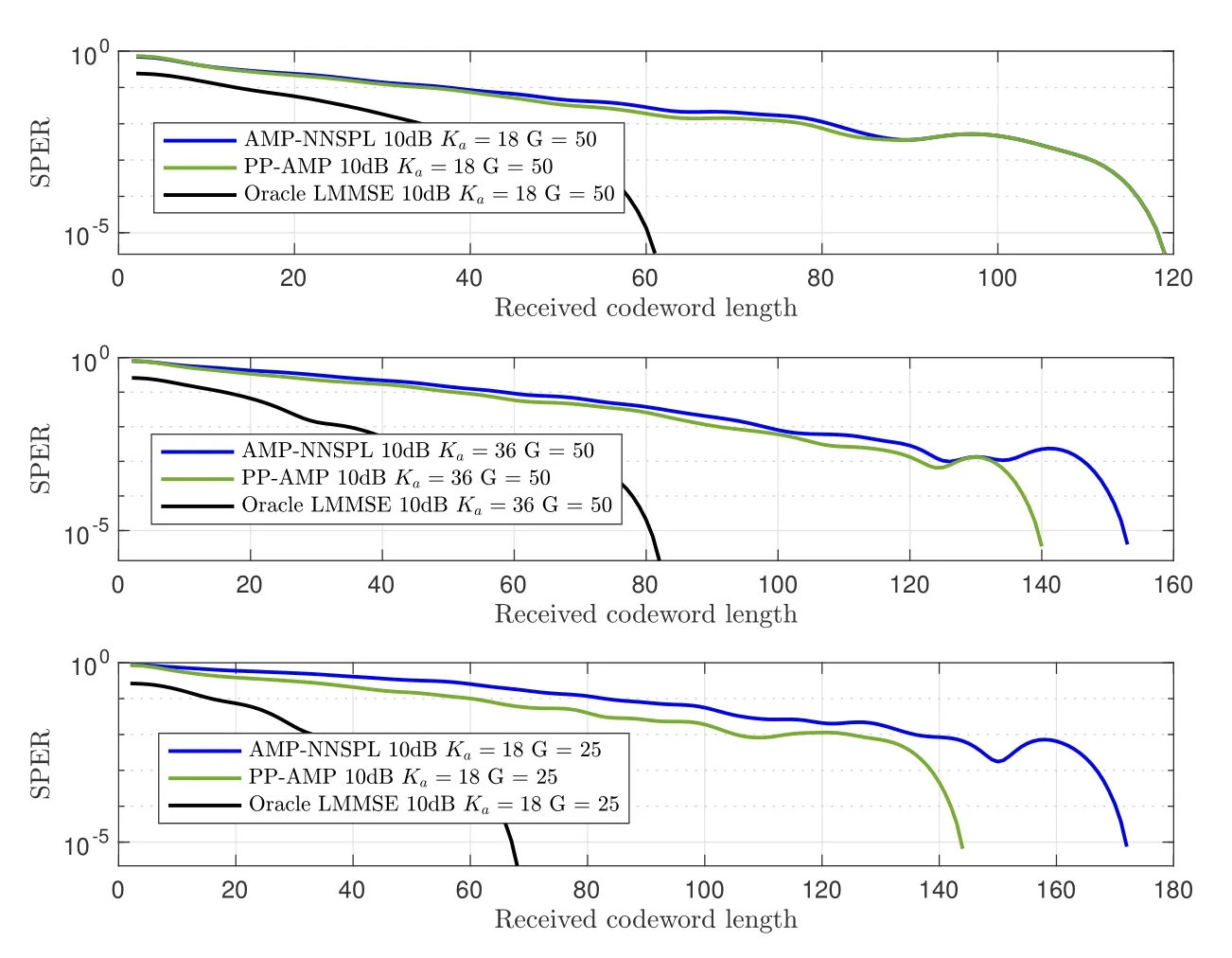
Figure 7. Comparison of SPER versus the length of received codeword length l for the proposed PP-AMP and the state-ofart AMP-NNSPL algorithms.

The results clearly demonstrate a trend where both NMSE-C and SPER decrease as the received codeword length increases,indicating that estimations for packets with longer codewords are more reliable.Notably,the NMSE-C and SPER of the PP-AMP algorithm exhibit a notably faster decrease,especially under conditions of fewer antennas or higher active probability.It is also worth noting that the NMSE-C and SPER of both AMP-NNSPL and PP-AMP algorithms are relatively higher than that of Oracle LMMSE,especially at small received codeword lengths.This might be due to the approximations of the original estimation problems in Eq.(12) and Eq.(14).Jointly estimation of the signal matrix and the latent activity modes through factor-graph-based inference techniques might alleviate this problem,which will be studied in future work.

Next,we proceed to compare the delay performance of both FA-GF-RMA and FS-GF-RMA.The FS-GFRMA scheme employed here is beacon-based,as described in [40],where the base station initiates transmission periods via downlink beacons.In this scheme,a user can only initiate access at the beginning of a transmission period.The receiver aims to decode all active users during a transmission period whenever additional Δ coded symbols are received.The transmission period concludes when all active users successfully decode their data or when the maximum codeword length is reached.In both schemes,the Oracle LMMSE algorithm provides the lower bound of delay achievable by any specific JADD algorithms.Notice that in FA-GF-RMA with Oracle LMMSE,the starting points are perfectly known.As for FA-GF-RMA with the AMP-NNSPL algorithm,the starting points are estimated by conducting the power-pattern-based activity mode estimation procedure afterward.

The overall delayDoencompasses the time duration from the moment a packet arrives until it is successfully decoded.The transmission delayDtis defined as the time interval from the point of packet access to successful decoding.The difference betweenDoandDtis the waiting delay.It’s worth noting that in FAGF-RMA,each packet initiates access upon reaching the buffer,provided the buffer is empty.As a result,Dtis almost equivalent toDoin FA-GF-RMA,i.e.,no waiting delay incurred,especially given a relatively low packet arrival rate.

Figure 8 illustrates the average delays at different SNRs with an antenna number ofG=50 and a packet arrival rate ofλ=0.0005 per symbol interval per user.As can be observed,the delays of the AMP-NNSPL and PP-AMP algorithms are close to each other,and both algorithms approach the lower bound as SNRs increase.This is because these algorithms demonstrate similar estimation performance,particularly at high SNRs and antenna numbers,as depicted in Figure 5.It’s essential to emphasize that,although the lower bound of transmission delay is smaller for FSGF-RMA compared to FA-GF-RMA,the substantial waiting delay in FS-GF-RMA,which accounts for approximately half of the transmission delay,results in a significantly longer overall delay compared to FA-GFRMA.

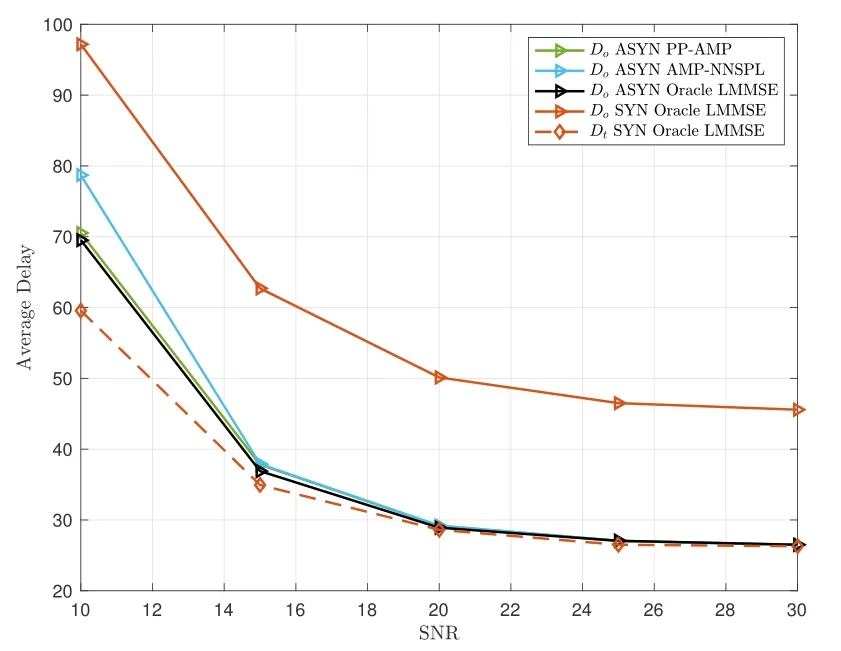
Figure 8. Comparison of average delays of FA-GF-RMA and FS-GF-RMA at different SNRs with G=50 and λ=5×10−4 packets per user per symbol interval.

Figure 9 provides a comparison of delays about the number of antennasG.The proposed PP-AMP algorithm approaches the delay achieved by Oracle LMMSE.However,it’s important to note that FA-GFRMA with the AMP-NNSPL algorithm becomes unstable when the number of antennas is less than 40.As a result,delay values for these configurations are not displayed.This instability arises because the NMSEC of the AMP-NNSPL algorithm decreases too slowly when the number of antennas is small,as depicted in the third sub-graph in Figure 6.Consequently,the decoder fails to decode packets and perform interference cancellation at a sufficient rate before more newly arrived packets enter the observation window.

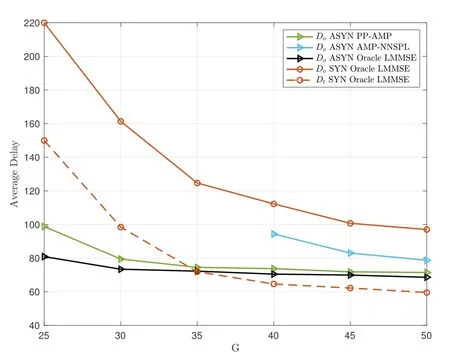
Figure 9. Comparison of average delays of FA-GFRMA and FS-GF-RMA at different antenna numbers with SNR=10dB and λ=5×10−4 packets per user per symbol interval.

To illustrate this,a sample trajectory of the number of active users in the observation window atG=30 is presented in Figure 10.As can be seen,with the AMPNNSPL algorithm,the number of active users continues to increase after surpassing 25,ultimately exceeding the total number of antennas,which is 30.It’s also worth noting that the count of active users in an observation window changes over time in FA-GF-RMA.When the system reaches a stable state,the average number of active users is roughly equivalent toλKDt,which is approximately 0.0005×500×80=20 in the example presented in Figure 10.

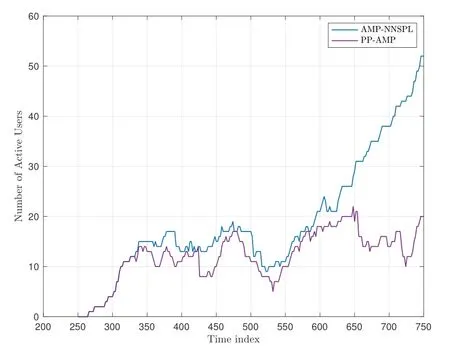
Figure 10. A sample trajectory of the number of active users versus time in FA-GF-RMA at G=30,λ=5×10−4 packets per symbol per user and SNR=10 dB.

Figure 11 illustrates the delays of both FA-GF-RMA and FS-GF-RMA using different algorithms versus the arrival rate.Similarly,the proposed PP-AMP algorithm exhibits delays close to the lower bound,while the AMP-NNSPL algorithm renders FA-GF-RMA unstable at high arrival rates.It’s also noticeable that FSGF-RMA is unstable,even with the Oracle LMMSE algorithm,at a high arrival rate of 0.0011 packets per symbol interval.The rationale behind this phenomenon is as follows: In FS-GF-RMA with Oracle LMMSE and a sufficient number of antennasG,the multi-user interference is nearly completely suppressed.Nevertheless,with an excessively high arrival rate,the number of newly arrived users during the current transmission period can surpassG,resulting in the degradation of interference suppression during the following transmission period.Consequently,the transmission period extends and encompasses even more newly arrived users,ultimately leading to system divergence.

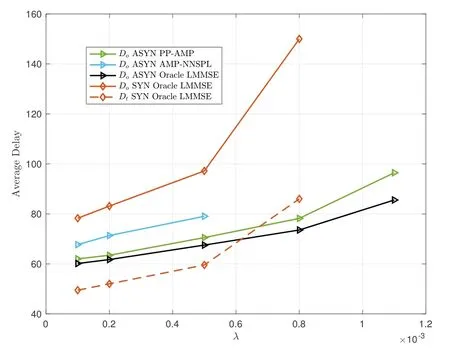
Figure 11. Comparison of average delays of FA-GF-RMA and FS-GF-RMA at different arrival rates with G=50 and SNR=10dB.

VI.CONCLUSION

In this work,a joint user activity and data detection algorithm is proposed for the FA-GF-RMA system.Considering the sparsity in user activities,an existing AMP-based algorithm for solving the JADD problem in synchronous grant-free access is directly applied.To address the limitation of the AMP algorithm in estimating the transmission starting point,the intrinsic power pattern in the rateless codeword is exploited to tackle this issue.Simulation results demonstrate that the proposed power-pattern-aided AMP algorithm outperforms the existing AMP-NNSPL algorithm in recovering the signal matrix with the unique sparsity structure observed in FA-GF-RMA.The delays achieved by the proposed solution in FA-GF-RMA with AFC approach the delay lower bound across various system configurations,verifying the proposed solution achieves the delay advantages of FA-GF-RMA over FS-GF-RMA in the practical scenario with unknown user activity information and practical rateless codes.

ACKNOWLEDGEMENT

This work is supported by the projects as follows,Key Research and Development Program of China (2018YFB1801102),Fundamental Research Funds for the Central Universities under Grant 2242022k60006,the Key Research and Development Program of China (2020YFB1806603),Tsinghua University-China Mobile Communications Group Co.,Ltd.Joint Institute,Civil Aerospace Technology Project (D040202),National Natural Science Foundation of China(Grant No.92067206,Tsinghua-Qualcomm Joint Project,Tsinghua University Initiative Scientific Research Program(20193080005).

NOTES

1It is assumed that the ACK is transmitted through an error-free channel with zero delays.

2Notice that an AFC-coded symbol is essentially the summation of independent random variables.According to the central limit theorem,when the degree is sufficiently large,the AFC-coded symbol approaches a Gaussian random variable.

3The optimization of pre-code,degree distribution and weight set are beyond the scope of this paper.