OFDMA-Based Unsourced Random Access in LEO Satellite Internet of Things

Jiaqi Fang ,Gangle Sun ,Wenjin Wang,* ,Li You ,Rui Ding

1 National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China

2 Purple Mountain Laboratories,Nanjing 211100,China

3 Institute of Telecommunication Satellite,CAST,Beijing 100094,China

Abstract: This paper investigates the low earth orbit(LEO)satellite-enabled coded compressed sensing(CCS)unsourced random access(URA)in orthogonal frequency division multiple access (OFDMA) framework,where a massive uniform planar array(UPA)is equipped on the satellite.In LEO satellite communications,unavoidable timing and frequency offsets cause phase shifts in the transmitted signals,substantially diminishing the decoding performance of current terrestrial CCS URA receiver.To cope with this issue,we expand the inner codebook with predefined timing and frequency offsets and formulate the inner decoding as a tractable compressed sensing (CS) problem.Additionally,we leverage the inherent sparsity of the UPA-equipped LEO satellite angular domain channels,thereby enabling the outer decoder to support more active devices.Furthermore,the outputs of the outer decoder are used to reduce the search space of the inner decoder,which cuts down the computational complexity and accelerates the convergence of the inner decoding.Simulation results verify the effectiveness of the proposed scheme.

Keywords: LEO;OFDMA;satellite;unsourced random access;UPA

I.INTRODUCTION

The Internet of Things (IoT) plays a pivotal role in 5G,aiming to provide services for massive devices to make the Internet more immersive and pervasive [1–3].However,current terrestrial networks,restricted by geographical limitations and high costs,struggle to serve remote areas like deserts,oceans,and forests.Recognizing the wide coverage of low earth orbit(LEO) satellites,the 3rd Generation Partnership Project(3GPP)has initiated a study on supporting the LEO satellite-enabled IoT networks with the 5G New Radio (NR) to provide services in these remote areas [4].In the wide coverage area of a single LEO satellite,there may be a vast number of devices to serve,with their data packets being sporadic and short[5].For such scenarios grant-based random access schemes result in significant excessive overhead,network congestion,and high transmission latency[6,7].To address this issue,there has been a surge in researches dedicated to incorporate the LEO satelliteenabled IoT networks with the grant-free random access,in which devices transmit signals to LEO satellites directly without a scheduling process[8–11].

Preceding researches mainly focus on integrating the grant-free sourced random access (SRA) with the LEO satellite-enabled IoT networks[8–11].Each device in the SRA should be allocated a unique pilot for the channel estimation (CE) and the active user dectection (AUD).As the number of devices in the LEO satellite-enabled IoT network proliferates,however,the SRA scheme becomes increasingly inefficient and unfeasible due to the arduous task of allocating unique pilots to each device.Alternatively,the grant-free unsourced random access (URA) is more competitive[12].In the URA scheme,all the devices share a common codebook,and the primary responsibility of the receiver is to recover the transmitted messages without necessarily identifying the specific devices.As it is independent from the number of devices in the network,the URA scheme,in theory,supports an unlimited number of devices[13–16].However,the original URA encounters a challenge in that its codebook size expands exponentially with the number of information bits transmitted,resulting in high decoding complexity [17].To mitigate this computational burden,the coded compressed sensing(CCS)URA is proposed to divide device messages into shorter segments,considerably reducing the codebook size [18–20].In current terrestrial IoT networks,CCS URA stands out for its low implementation cost[21–25].Considering the power limitations of LEO satellites,investigating the CCS URA is crucial for the LEO satellite-enabled IoT networks[26].

In order to mitigate the implementation costs and optimize the interaction procedure,it is essential for the LEO satellite-enabled IoT networks to exploit the technology commonalities with the current 5G NR,where the orthogonal frequency division multiple access (OFDMA) is adopted [3].In this context,we propose the LEO satellite-enabled CCS URA scheme in the OFDMA framework,where a massive uniform planar array (UPA) is equipped on the satellite for improving the system spectral and energy efficiency[27,28].In LEO satellite communications,long propagation delay and large Doppler frequency offset,attributable to the long transmission distance and the high relative speed between the satellite and devices,can be mitigated to an extent through the precompensation at the device side [26].However,for IoT devices operating under stringent cost constraints,residual timing and frequency offsets after compensation are inevitable [29,30].These residuals induce phase shifts in signal transmissions,rendering conventional terrestrial CCS URA receivers ineffective.We delve into addressing this challenge,and our primary contributions are summarized as follows:

• We propose the OFDMA-based CCS URA scheme for the UPA-equipped LEO satelliteenabled IoT networks.

• We expand the inner codebook with predefined timing and frequency offsets,and then formulate the inner decoding as a tractable compressed sensing(CS)problem.

• By harnessing the intrinsic sparsity of the UPAequipped LEO satellite angular domain channels,we design an outer decoder that leverages the discriminating power of the angles to supprot more active devices.

• Building on the proposed inner decoder and outer decoder,a joint inner and outer decoder is proposed to further enhance the system performance,where the output of the outer decoder are employed to reduce the search space of the inner decoder,thereby reducing the computational complexity and facilitating the convergence of the inner decoding.

The rest of this paper is organized as follows: Section II illustrates the system overview and the channel model.The details of the proposed OFDMA-based CCS URA is given in Section III.Section IV elaborates the design of the receiver.Numerical simulation results are presented in Section V.Finally,Section VI concludes this paper.

II.SYSTEM MODEL

2.1 System Overview

In the considered scenario,a LEO satellite equipped with a half-wavelength spacedM=MxMyUPA provides services toKtotsingle-antenna devices.Within a given time interval,Ka≪Ktotdevices are active and send messages to the LEO satellite.Taking into account the implementation cost,we propose the OFDMA-based CCS URA scheme for this LEO satellite-enabled network,where all active devices transmit on the shared OFDMA resource elements.Within the OFDMA resource elements grid,an OFDM symbol encompassesNTsubcarriers,in whichNcadjacent subcarriers are available for active devices.The transmission of each active device occupies the sameNsymOFDM symbols,i.e.,the total number of available resource elements isNcNsym.

DenoteLas the set of messages transmitted by active devices.The system performance is expressed in terms of the PUPE

2.2 Channel Model

In light of the considerable altitude of the LEO satellite,it is reasonable to posit that the angles of arrival(AoA) of all propagation paths emanating from the same device are congruent.Following this,the channelhk∈CM×1of device-kcan be written as[27]

where⊗represents the Kronecker product,βkrepresents the channel gain exhibiting the Rician fading distribution with the Rician factorκ,i.e.,

III.OFDMA-BASED CCS URA

Following the works in[13],we propose the OFDMAbased CCS URA scheme shown in Figure 2,which includes the outer encoding,the inner encoding,the OFDMA mapping,the inner decoding,and the outer decoding processes.The outer encoder partitions original messages into numerous segments,each of which is appended with parity check bits.Subsequently,in the inner encoding process,the outer codewords are mapped to codewords in a common inner codebook,which will be further mapped to different OFDMA resouce elements to be transmitted.Upon successful transmission,the inner decoder identifies the transmitted segmented messages,and then the outer decoder stitches these segmented messages to recover the origianl messages.

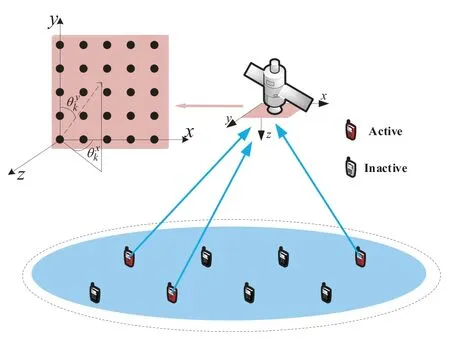
Figure 1. The LEO satellite-enabled CCS URA system.

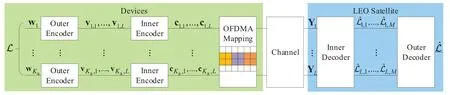
Figure 2. The block diagram of the OFDMA-based CCS URA.

3.1 Outer Encoding

Letwk∈{0,1}B×1denote the original message of device-k.In the outer encoding process,wkis divided intoLsegments,i.e.,wk,1,wk,2,...,wk,L,wherewk,l∈and=B.The parity check bitspk,l∈is generated by

whereGl,i∈is the generation matrix whose elements follow the Bernoulli distribution with the parameterindependently,andpk,lis computed using modulo-2 arithmetic which makespk,lremain binary.Subsequently,pk,lis appended towk,lto form the fixed-length outer codewordvk,l∈{0,1}J×1,whereJ=Bl+Pl,i.e.,

3.2 Inner Encoding

The inner encoder maps the outer codewordvk,lto the inner codeword employing the inner codebookA∈,whereAis a Gaussian random matrix with entries followingCN(0,) andR=[13].More precisely,the inner codewordck,l∈CR×1of device-kin segment-lis given by

wheremk,l∈denotes the inner codeword indicator vector with only its((vk,l)b→d+1)-th entry being one,and (·)b→ddenotes the binary to decimal conversion.

3.3 OFDMA Mapping and Signal Transmission

In the OFDMA mapping process,the inner codewords are mapped to the OFDMA resource elements for being transmitted to the LEO satellite.As illustrated in Figure 3,the inner codewordck,lis uniformly devided intoNs=fragments,i.e.,=ck,l,1,ck,l,2,...,,and thenck,l,t=∈=is transmitted over the ((l−1)Ns+t)-th OFDM symbol.

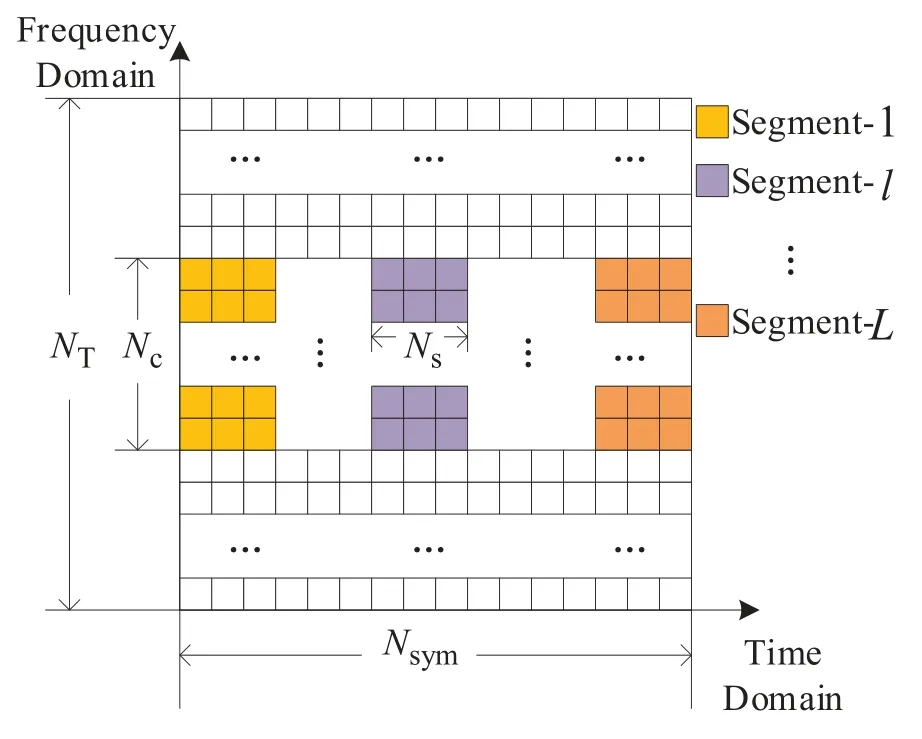
Figure 3. The OFDMA resource elements grid.

In LEO satellite communications,long propagation delay and large Doppler frequency offset can be ameliorated to a certain degree via the pre-compensation mechanism implemented on the device side.However,for cost-constrained IoT devices,residual timing and frequency offsets persist following the compensation process.Letτk∈{0,1,...,τmax} andϵk∈[−ϵmax,ϵmax]denote the inevitable residual timing and frequency offset coefficients of device-k,respectively.The frequency domain received signals of thel-th segment(specifically,the signals received over the((l−1)Ns+1)-th to thelNs-th OFDM symbols)Yl∈CR×Mcan be written as[3]

whereKawith the cardinality |Ka|=Karepresents the active devices set,Zl∈CR×Mrepresents the noise matrix with its entries independently followingCN(0,),Dk,l∈CR×Rrepresents the phase shift matrix associated withck,l,which is given by

the phase shift matrixDk,l,t∈associated withck,l,tis given by

Ncprepresents the length of the cyclic prefix,andQk∈represents theτkleft cyclic shift matrix.

IV.RECEIVER DESIGN

4.1 Inner Decoding

To overcome the path loss challenge in LEO satellite communications,the receiving beamforming technique is often adopted.Given the innate directivity of the UPA-equipped LEO satellite channels,we employ the beamforming method rooted in the extensively utilized DFT beamforming codebook [27].DenoteF=Fx⊗Fyas the beamforming codebook,whereFd∈,d=x,y,represents theMd-point DFT matrix.Subsequent to the receiving beamforming process,the angular-frequency domain received signals∈CR×1of angle-sin segment-lcan be written as

The role of the inner decoder is to recover the set of the transmitted outer codewordsLl=Ll,1∪Ll,2∪···∪Ll,M,whereLl,s={vk,l|k ∈Ka,s}.For conventional terrestrial IoT networks,where the phase shift matrixDk,lcan be represented as an identity matrix,the estimation ofLl,scan be obtained employing the direct CS method based on (10) [13].However,for the LEO satellite-enabled IoT networks,the presence of the unknownDk,lmakes the direct CS method inapplicable.To circumvent this obstacle,we expand the inner codebookA=[a1,a2,...,]with predefined timing and frequency offsets,and then formulate the inner decoding as a tractable CS problem.

To build the inner decoding model,we postulate that the timing and frequency offsets for the active devices are uniformly distributed within the discrete setsT={η1,η2,...,η|T|} andE={ν1,ν2,...,ν|E|},respectively.It should be highlighted that this assumption is employed primarily to facilitate building the inner decoding model,rather than representing an inherent property of the timing and frequency offsets.With a little bit of notations abusing,denoteEl,i,jas the phase shift matrix,where the timing and frequency offsets areηiandνj,respectively.In essence,El,i,jis obtained by replacingτkandϵkinDk,lwithηiandνj,repectively.We expandAto

for thel-th segment,where∈CR×|T||E|is given by

As a result,the signal transmission model(10)can be rewritten as

where the timing and frequency offsets indicator vectorek∈{0,1}|T||E|×1has only one non-zero entry whose index indicates the timing and frequency offsets of device-k,andis a sparse vector.

Denotegl,s=withgl,s,b∈C|T||E|×1.It is important to note that,in our model,”gl,s,b0” implies that there exists at least one device from the setKa,stransmittingabin segment-l.Therefore,the inner decoding is equivalent to the estimation ofgl,sbased on (13),which is a traditional CS problem.We resort to the AMP algorithm in[31]to obtain the log-likelihood ratiorl,s∈with its entry being

Then,the inner decoding results of angle-sin segment-l(i.e.,the estimationofLl,s),is given by

where(·)d→brepresents the decimal to binary conversion.

4.2 Outer Decoding

The outer decoder should stitch the candidate outer codewords from the inner decoders across different segments together for reconstructing the original messages.The traditional tree outer decoder in the CCS URA[13]achieves this task relying solely on the discriminating power of the parity check bits.Nevertheless,such mechanism will end up with incorrect decoding results when the number of active devicesKaexceeds the discriminating power of the parity check bits.The sparsity of the UPA-equipped LEO satellite angular domain channels indicates that the discriminating power of the angles can be employed as an additional tool to stitch the candidate outer codewords.With the discriminating power of the angles,wrong decoding results will only occur when the active devices number |Ka,s| ＜Kaof angle-srather thanKasurpasses the discriminating power of the parity check bits.In light of this,we perform the tree outer decoding in the angular domain.Based on,the tree outer decoding is performed for getting the outer decoding resultsof angle-s(i.e.,the estimation ofLs={wk|k∈Ka,s}).Then,the outer decoding result(i.e.,the estimation ofL={wk|k∈Ka}) is obtained by aggregating the results corresponding to all angles i.e.,.

Specifically,for any angles: Each outer codewords inis chosen as a root node.For each root node from,there arecandidate outer codewords to be stitched in segment-2,thus formingpaths.Then,the valid paths fulfilling(4)are retained.Denote the set of the valid paths in segment-2 as.Accodingly,there existpaths in segment-3.Once more,reserve the valid paths matching(4)to get the set of the valid paths in segment-3,denoted as.This segment-by-segment progression continues up until segment-L.Then,is obtained by extracting the message parts of the valid paths set.

We summarize the proposed decoding algorithms in Section 4.1 and Section 4.2 as Algorithm 1.

4.3 Joint Inner and Outer Decoding

To further improve the decoding performance and reduce the decoding complexity,we propose the joint inner and outer decoder on the basis of the decoding process proposed in section 4.1 and section 4.2.Based on,the joint inner and outer decoder outputs the estimation,and thenis get by combining the results of all angles,i.e.,.As depicted in Figure 4,the operation of the inner and outer decoders is orchestrated in an alternating manner.The output of the outer decoder are utilized to reduce the search space of the inner decoder,thus reducing the computational complexity and facilitating the convergence of the inner decoding.For the sake of argument,we will detail the decoding procedure specific to angle-sin segment-(l+1)in the remainder of this section.

Denote then-th valid path in the valid paths setof angle-sin segment-las

wherevl,s,n,i∈{0,1}J×1represents thei-th outer codeword from the inner decoding of segment-iassociated with the valid path.According to the parity check equation (4),the check components for the transmitted outer codewords of angle-sin segment-(l+1),which can be stitched to the valid path,are confined within the check pattern:.Consequently,any transmitted inner codewordabof angle-sin segment-(l+1)must adhere to the condition:

In segment-(l+1),we prune the inner codebookAtoAl+1,s∈by only reserve the inner codewords that comply with (17),where the dimensionKl+1,s≤2J.Following this pruning operation,we expandAl+1,stowith the predefined timing and frequency offsets to acquire the inner decoding resultof angle-sin segment-(l+1)(See section 4.1.),and then the valid paths setof angle-sin segment-(l+1) is obtained with the tree outer decoder(See section 4.2.).It is pertinent to note that the search space in segment-(l+1)’s inner decoding of angle-shas been reduced form 2J|T||E|toKl+1,s|T||E|.

Remark 1.Given the sparsity of UPA-equipped LEO satellite channels in the angular domain,|Pl,s|is significantly less than |Pl,1∪Pl,1∪··· ∪Pl,M|.The result suggests that angle distinctiveness aids in further pruning the inner codebook,thereby reducing the computational complexity and facilitating the convergence of the inner decoding.

The proposed joint inner and outer decoding algorithm is summarized in Algorithm 2.

V.SIMULATION RESULTS

In this section,we provide numerical simulations to evaluate the performance of the proposed OFDMAbased CCS URA scheme in the LEO satellite IoT network.The energy per bit to noise power spectral density ratio is given by

The OFDMA-based CCS URA is configured as follows: The length of original message isB=24,the number of segment isL=7,the length of the outer codeword isJ=9,the lengths of the parity check bits are [P1,P2,P3,P4,P5,P6,P7]=[0,5,5,5,6,9,9],the number of the total subcarriers isNT=2048,the length of the cyclic prefix isNcp=144,the number of the available subcarriers isNc=72,the available subcarriers indices are 1001,...,1072,and the number of OFDM symbols for transmission isNsym=14.Besides,the channel Rician factor is set asκ=10dB,the physical angle,∀kand,∀kare uniformly distributed in(−1,1][27],devices’timing offsetsτk,∀kand frequency offsetsϵk,∀kdistribute uniformly in {0,1,...,τmax} and [−ϵmax,ϵmax],whereτmax=20 andϵmax=0.2[32].In the proposed receiver,we setT={0,5,...,20} andE={−0.2,−0.1,...,0.2}.

We compare the following decoding schemes,with their respective computational complexities delineated in Table 1.

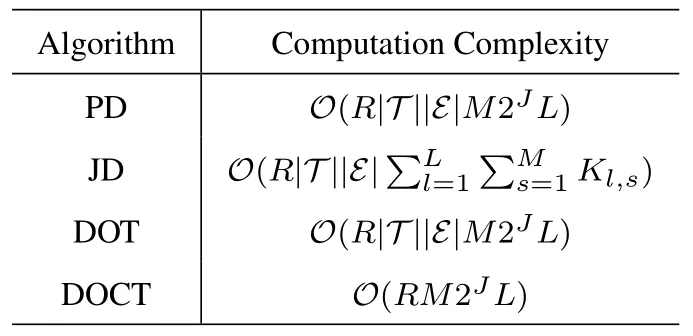
Table 1. Computational complexity of different decoding schemes.

1.Proposed decoding algorithm in section 4.1 and section 4.2(PD).

2.Joint inner and outer decoding algorithm in section 4.3(JD).

3.Decoding with original tree outer decoder(DOT):This method aligns closely with the PD,with the key distinction that the outer decoding in DOT exclusively utilizes the distinguishing capacity of the parity check bits(In essence,it inputs,l=1,...,L,to the tree outer decoder to directly get.).

4.Decoding with original inner codebook and original tree outer decoder(DOCT):The DOCT is the conventional terrestrial CCS URA decoder [13].It parallels the DOT,but the inner decoding in DOCT employs the original inner codebookA,as opposed to the expanded inner codebook.

In Figure 5,we assess the PUPE performance for various algorithms under the assumption of zero timing and frequency offsets.The result validates the effectiveness of the baseline DOCT approach.Additionally,in the absence of the timing and frequency offsets,the performance of DOCT is equivalent to that of DOT.Figures 6 through 8 illustrate the performance of the proposed OFDMA-based CCS URA under conditions involving timing and frequency offsets.In Figure 6,the decoding performance of several algorithms is investigated against the variation in the number of active devices.We can observe that the DOCT is almost ineffectual.All the algorithms manifest degradation in performance with the increase of the number of active devices.Comparing the DOT and the DOCT,it can be inferred that the expanded inner codebook significantly mitigates the effects of timing and frequency offsets.Moreover,the distinguishing capacity of the angles enables the PD to outperform the DOT.Due to the reduced search space which expedites the convergence of the inner decoding,the JD with lower computational complexity,demonstrates superior performance compared to the PD.Figure 7 shows the performance of different algorithms with respect to the number of antennas.As the number of antennas escalates,the distinguishing power of the angles is progressively augmented.This results in a widening performance gap between the DOT and the proposed algorithms PD and JD.Figure 8 illustrates the decoding performance of several algorithms against the.The proposed algorithms PD and JD outstrip the baseline algorithms across an extensiverange.Furthermore,consistent with previous observations,the proposed JD algorithm achieves the optimal performance.

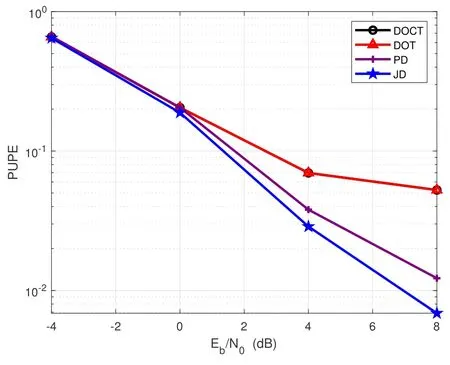
Figure 5. The PUPE of different decoding schemes versus,where Ka=50 and Mx=My=4.

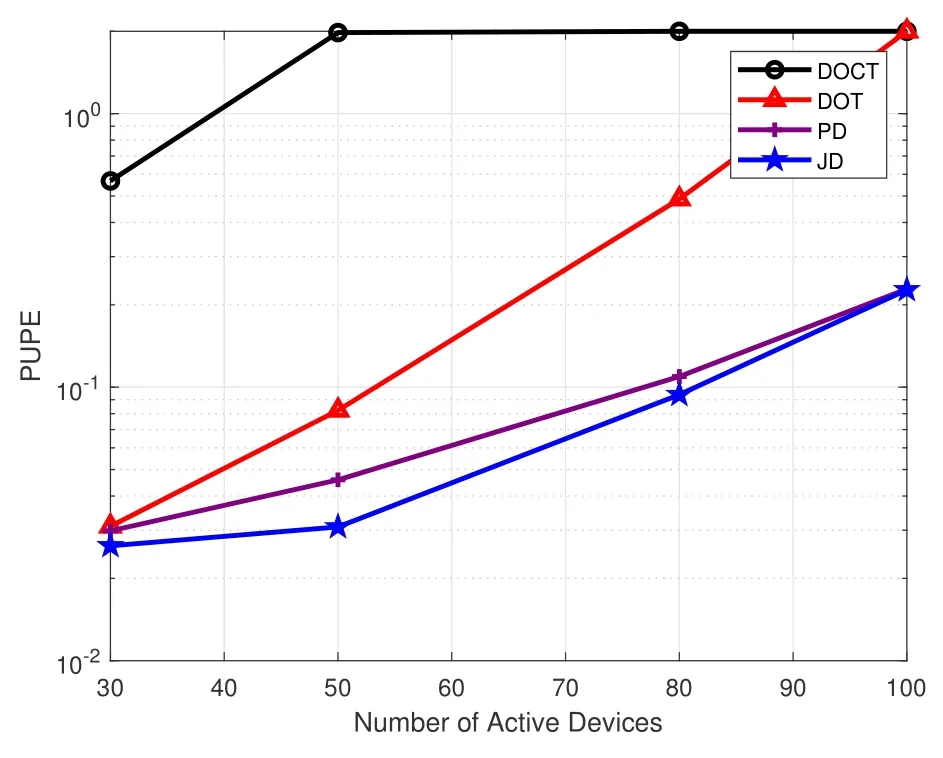
Figure 6. The PUPE of different decoding schemes versus the number of active devices Ka,where =5dB and Mx=My=4.

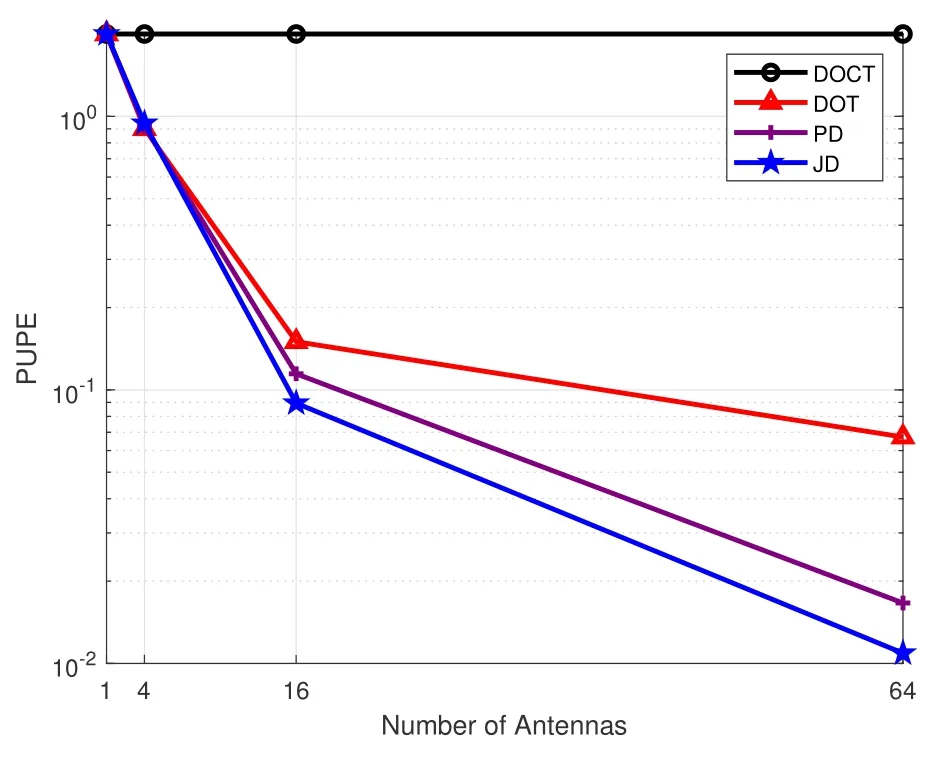
Figure 7. The PUPE of different decoding schemes versus the number of antennas M,where Mx=My=,=3dB,and Ka=50.

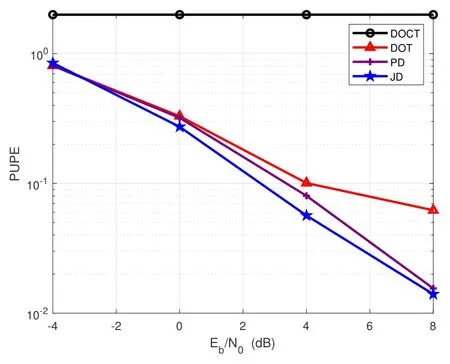
Figure 8. The PUPE of different decoding schemes versus,where Ka=50 and Mx=My=4.

VI.CONCLUSION

In this paper,we combined the CCS URA and the LEO satellite communication in the framework of the OFDMA to serve massive devices in remote areas.With the presence of the inevitable timing and frequency offsets,we formulated the inner decoding of the CCS URA as a soveable CS problem,and proposed the angular domain outer decoding algorithm.Then,the joint inner and outer decoding algorithm was proposed to reduce the computational complexity and further improve the system performance.Simulations revealed the effectiveness of the proposed scheme.

ACKNOWLEDGEMENT

This work was supported by the National Key R&D Program of China under Grant 2023YFB2904703,the National Natural Science Foundation of China under Grant 62341110,62371122 and 62322104,the Jiangsu Province Basic Research Project under Grant BK20192002,and the Fundamental Research Funds for the Central Universities under Grant 2242022k30005 and 2242023K5003.