A Blind Batch Encryption and Public Ledger-Based Protocol for Sharing Sensitive Data

Zhiwei Wang,Nianhua Yang,Qingqing Chen,Wei Shen,Zhiying Zhang

1 School of Computer Sciences,Nanjing University of Posts and Telecommunications,Nanjing 210023,China

2 Dept.of Intelligent Science and Information Law,East China University of Political Science and Law,Shanghai 201620,China

3 Key Laboratory of Computational Science and Application of Hainan Province,Hainan Normal University,Haikou 571158,China

4 State Key Laboratory of Public Big Data,Guizhou University,Guizhou 550025,China

5 Yunnan Key Laboratory of Blockchain Application Technology,Yunnan Innovation Research Institute of Beijing University of Aeronautics and Astronautics,Kunming 650233

Abstract: For the goals of security and privacy preservation,we propose a blind batch encryption-and public ledger-based data sharing protocol that allows the integrity of sensitive data to be audited by a public ledger and allows privacy information to be preserved.Data owners can tightly manage their data with efficient revocation and only grant one-time adaptive access for the fulfillment of the requester.We prove that our protocol is semanticallly secure,blind,and secure against oblivious requesters and malicious file keepers.We also provide security analysis in the context of four typical attacks.

Keywords: blind batch encryption;data sharing;onetime adaptive access;public ledger;security and privacy

I.INTRODUCTION

Many Internet of things (IoT) applications,such as smart homes [1],smart transportation [2] and smart cities [3],are significantly changing our lives [4–6].IoT devices generate massive quantities of measured data every day,but determining how to share these data,especially sensitive data,is a major problem.Ideally,the data owner should be able to give onetime adaptive access,which means that access is only granted for a small part of the data when it is really needed for the fulfillment of service.When the service is finished,the corresponding parts of the data should be revoked from the requester’s database.Public ledgers based on blockchains [7] provide a good solution for this problem and can guarantee the immutability and accountability of the data.However,security and privacy preservation are great challenges when a pubic ledger is used to store sensitive data,such as patient health records in smart health systems[8–10].This kind of data should not be tampered with.Furthermore,in some cases,the requester should only have access to certain parts of the data [11–13].For example,if a cardiologist requests patient Bob’s health records in a hospital (data owner),then it may be disclosed that Bob has heart disease.According to the security definition,blind batch encryption scheme[14,15]may be a great solution for privacy preservation.

The approach used to realize a one-time adaptive access system is based on the fact that it is usually expensive to maintain a local copy of the data and that the requester avoids copying the data that have been accessed.Riccardo et al.recently proposed a public ledger with one-time access [16].In their system,they encrypt plaintext with a one-time-pad scheme.To maintain the one-time access property,the pad is periodically regenerated so that a new key is needed to decrypt the data again.However,there is a shortcoming in their system: when the requester makes an access request to the data,the data owner sends the whole one-time-pad ciphertext as well.Usually,the size of data sets is very large,and thus,the communication costs are very high.Our idea is that the data owner only sends a small part of the one-time-pad ciphertext that can satisfy the fulfillment of the requester and that other parts of the data need not be sent to the requester.

Another cryptographic primitive used in our system is blind batch encryption,which is the blindnesspreserving version of a batch encryption primitive[14,15].If a random plaintext is encrypted by a blind batch encryption scheme,then the ciphertext is completely independent of the public key and the plaintext.Blind batch encryption is a great solution for balancing security and privacy in our system,which not only protects the ciphertext but also hides both the public keys and the identities of the requesters.

The scenario in our system is as follows: a data owner D stores its data safely in the cloud with the option to share some parts of the information with a requester R for some time with the guarantee that an independent third party can audit the integrity of the data.This third party is called the public ledger.Another party called the file keeper F should maintain the storage and revocation mechanism,which is not responsible for the confidential property,so it is not a trusted third party.To save on storage costs of the public ledger,the encrypted data should be stored on less expensive space for remote access,and the metadata used to audit the integrity of the data and the behaviors of F should be stored in the public ledger.This kind of metadata includes an encryption token used to synchronize with updating of the ledger and D’s encapsulated session keys.To share a small part of the data with R,D encrypts the corresponding part of the ciphertext using the blind batch encryption scheme,generates unlock keys using its current encapsulated session keys and then sends them to R.Anyone,even D,cannot know exactly which parts of the data R has accessed,and the unlock keys are automatically revoked after F updates the public ledger.

The contributions of this paper are as follows.1)We propose a blind batch encryption and public ledgerbased protocol for the sharing of sensitive data.Our protocol not only assures the integrity of the sensitive data using a public ledger but also achieves privacy preservation using the blind batch encryption scheme.2) We prove that our protocol is semantically secure,blind,and secure against oblivious requesters and malicious file keepers.We also analyze the security properties in the context of four typical attacks.The implementation of our protocol shows the communication and computation costs of our protocol on resourcelimited platforms.

Organization.Related preliminary concepts are introduced in Section II.A blind batch encryption and public ledger-based protocol for the sharing of sensitive data is proposed in Section III.The security proofs for four properties are proposed in Section IV.The security and privacy-preserving analysis of our protocol in the context of four typical attacks are presented in Section V.The performance analysis of our protocol is presented in Section VI.Finally,we conclude our paper in Section VII.

II.PRELIMINARY

2.1 Mathematical Assumption

Definition 1(Bilinear Pairing).Let G and GTbe the cyclic groups with the same order p and a bilinear map e that is defined as e : G×G→GTand has the following properties:

• Bilinear property: ∀g,h ∈G and ∀a,b ∈Zp,e(ga,hb)=e(g,h)ab.

• Nondegeneracy property: for a generator g ∈G,e(g,g)1G.

Definition 2(Computational Diffie-Hellman(CDH)Assumption[17,18]).The CDH assumption over group G states that,for any probability polynomialtime (PPT) attackers,given a tuple (g,ga,gb) ∈G3for a randomly chosen a,,the advantage for obtaining a solution gabis negligible in λ.

Definition 3(Decisional Bilinear Diffie-Hellman(DBDH) Assumption[16]).Let a,b,s,z ∈ Zpbe chosen at random and g be a generator of G.Let A=ga,B=gb,S=gs.The DBDH assumption states that for any probability polynomial-time(PPT)attackers,given two tuples(A,B,S,e(g,g)abs)and (A,B,S,e(g,g)z),the advantage of distinguishing these two tuples is negligible.

Definition 4(Interactive Decisional Diffie-Hellman(IDDH)Assumption[16]).There are two roles in the IDDH assumption.One is a challenger,C,and the other is a simulator,B,who interacts with C as follows.

• C randomly chooses a,b,z ∈Zpand g is a generator of group G.

• C sends A=ga,B=gbto B.

• B randomly chooses s ∈Zpand sends S=B1/sto C.

• C chooses a random bit ι ∈{0,1} and answers B with Z=Sa=gab/sif ι=0 and Z=gzif ι=1.

• Given(A,B,S,Z),B outputs a guess ι′for ι.The IDDH assumption states that for any probability polynomial-time (PPT) simulators,the probability that Pr[ι′=ι]−1/2 is negligible.

2.2 Goldreich-Levin Hardcore Bit-based One-Time Encryption

The one-time encryption scheme based on the Goldreich-Levin hardcore bit[19]consists of three algorithms.

Setup(1l):This algorithm outputs a secret key x ∈{0,1}lfor a security parameter l.

Enc(x,µ):This algorithm takes the secret key x and a one-bit plaintext µ ∈{0,1} as input and then chooses a random bit string α ∈{0,1}l.It computes ＜ α,x ＞as an inner product over the binary field and the ciphertext ct=(α,σ=＜α,x ＞⊕µ)where ＜α,x ＞.

Dec(x,ct):This algorithm takes the secret key x and the ciphertext ct=(α,σ)as input and outputs the plaintext as σ⊕＜α,x ＞.

It always holds that Dec(x,Enc(x,µ))=µwith a probability of 1 for all x,µ.The Goldreich-Levin Theorem[19]proves that Enc(x,µ)is uniformly random regardless of x ifµis random.

2.3 Definition of l×2 Blind Batch Encryption

In l×2 blind batch encryption[13],the plaintext M is formalized as an l×2 matrix.The secret key x should be parsed as x ∈{0,1}l,and only the decryptor with x can obtain exactlyfor each row of M.A blind batch encryption scheme typically consists of six algorithms as follows[15].

Setup(1λ,1n):This algorithm outputs a common reference string crs for the security parameter λ and the key length n.

Gen(crs,x):This algorithm takes the common reference string crs and the secret key x as input and outputs the corresponding public key h.

SingleEnc(crs,h,i,Mi):This algorithm takes the common reference string crs,the public key h,an index i ∈{1,···,l}and a single row of plaintext Mi=(Mi0,Mi1)as input and outputs the ith single ciphertext cti,which can be written in two parts as cti=(cti0,cti1) for the blindness property.Enc(crs,h,M):This algorithm takes a matrix M ∈Gl×2as input.For each row of M,the algorithm runs the SingleEnc algorithm to obtain the single ciphertext ctiand outputs the final ciphertext ct={cti}i∈{1,···,l}.

SingleDec(crs,x,i,cti):This algorithm takes the common reference string crs,the secret key x,an index i ∈{1,···,l}and a single ciphertext xias input and outputs the ith single plaintext.

Dec(crs,x,ct):This algorithm takes the common reference string crs,the public key h and the ciphertext ct as input and runs the SingleDec algorithm to obtain each single plaintext.Finally,it outputs the plaintext Mx=.

III.DESIGN OF THE PROTOCOL

In this protocol,a data owner D publishes its encrypted data on a public ledger that is maintained by a file keeper F.To gain access to a small part of the encrypted data,a requester R should ask D for a decrypting key with some masking shards that are published in the public ledger.To protect privacy information,the requester cannot ask the data owner directly but must use the blind batch encryption scheme.F should update the masking shards periodically,and thus,the older decryption keys will become invalid.Our protocol is an improvement of the Riccardo et al.protocol [16].There are two differences for our protocol.The first difference is that D should be able to grant one-time adaptive access to R but not one-time access,which means that D can only grant partial access privilege to R for the fulfillment of R.The second difference is that R must make the request to access the data using blind batch encryption for privacy preservation.Let the plaintext M be an n×2 matrix;then,the protocol can be described as follows.

Step 1:In this step,F will setup the public ledger and publish the initial masking shards.It takes as input a security parameter λ and generates a bilinear group G with a prime order p,where g is a generator of G.Let e : G×G→GTbe the bilinear pairing and GThave the same order p as G.F randomly chooses ui∈Zpfor 1 ≤i ≤n where n is the number of rows in the plaintext matrix.Finally,F randomly chooses an initial time key∈Zpand publishes the initial masking shards1 ≤i ≤n,and(G,p,g,e).

Step 2:F should update the masking shards periodically by choosing a new time key∈Zpand computing,1 ≤i ≤n.

Step 3:D chooses two secret values µ,ν ∈Zpand sets up his or her public key as q=gµ.

Step 4:To put an encrypted file on the public ledger at time tj,D asks F for an encryption token.F uses the public key of D to compute the token as.

Step 5:Let Mi=(Mi0,Mi1)be the ith row of plaintext M.When D wants to encrypt Mi(1 ≤i ≤n) at time tj,it first selects two random values k0,k1∈Zpand computes the ciphertexts as follows:

where ci1=for 1 ≤i ≤n.After receiving the encrypted shards,F inserts them into the next block of the public chain.

Step 6:In this step,D computes the encapsulated keys at time tjby using its secret value ν,

After receiving the encapsulated keys,F inserts them into the updated public ledger.

Step 7:For the last row of the plaintext matrix,F computes the control shards,

Then,F inserts the control shards into the updated public ledger.

Step 8:Once the encrypted plaintext M has been published,F should periodically update not only the masking shards as in Step 2 but also the encapsulated keys asfor b ∈{0,1}.

Step 9:D only authorizes R to access a small part of the plaintext M,and R does not want others to know which parts of M it will access.We assume that R is only granted access to the plaintext blocks from γ to θ where 1 ≤γ ＜θ ≤n,and |θ−γ|=l ≪n.For privacy preservation,an l × 2 blind batch encryption scheme [13] is used for accessing encrypted data.R first chooses αi∈Zpfor γ ≤i ≤θ and publishes gi=for γ ≤i ≤θ.Following this,R selects an l-bit secret key x,where the ith bit of x is denoted by xi,and only R can obtain exactlyfor each row of M in the blind batch encryption scheme.Finally,R computes its public key as h=and sends it to D.

Step 10:D randomly chooses r ∈Zp.For all ji and b ∈{0,1},D computesand gib=.Following this,it computes vib=gib·cibfor b ∈{0,1} and i=γ,···,θ.Then,to grant a one-time adaptive permission,D computes the unlocked keys for the current time tjfrom the encapsulated keyin the updated ledger.The unlocked keycan be computed as follows:

Finally,D sends

to R.

Step 11:By using its secret key x and the unlocked keys at time tj,R can decrypt the ciphertexts.First,it computes,and then,it obtainsfor i=γ,···,θ.Second,it computes

IV.SECURITY PROOF

4.1 Semantic Security

We define the semantic security of our protocol as follows,which is similar to the security definition of blind batch encryption[15,13].

Definition 5.The semantic security of our protocol can be defined using the following game between a challenger C and an attacker A.

Setup:For the security parameter 1l,the attacker A chooses a secret key x with length l and sends it to the challenger C.

Challenge:For the security parameters 1λand 1l,C generates a common reference string crs and sends it to A.A chooses c(0),c(1)∈{0,1}l×2such thatfor each row ofand sends them to C.C computes the public key h,chooses a bit β and encrypts vβ=Enc(crs,h,c(β)).C then sends{vβ}β∈{0,1}to A.

Output:A outputs a guess bit β′for β;if β′=β,then the attacker wins the game.

We define the advantage of a probability polynomialtime (PPT) attacker as.If−1/2|≤1/poly(λ),then we say that our protocol is semantically secure.

Theorem 1.Our protocol is semantically secure under the CDH assumption.

Proof.From the security definition,if an attacker,A,can distinguish two challenging ciphertexts,then it wins the game.In our protocol,if A can distinguish,then it is equivalent to distinguishing two challenging ciphertexts,and it also can win the game since the ciphertext is vib=.To prove this theorem,consider the following game between a challenger,C,and an attacker,A.

Setup:The attacker,A,chooses x ∈ {0,1}land i ∈{γ,···,θ}.Next,it sends (n,x,i) to the challenger,C.

4.2 Blind Property for Privacy Preservation

In this section,we define the blindness property for privacy preservation as follows,which is similar to the blind definition in[15,16].

Definition 6.Suppose the ciphertext v of our protocol can be written in two parts(v1,v2);then,the encryption algorithm can also be decomposed into two parts,Enc(crs,h,c;r)=(ct1=Enc1(crs;r),ct2=Enc2(crs,h,c;r)).Obviously,v1is independent of both the public key and the plaintext.Furthermore,our protocol should be satisfied that no PPT attacker A can win the following game with the probability≥1/2+1/poly(λ).

Setup:The attacker A takes the secure parameters 1λand 1las input and sends the secret key x with length l to the challenger C.

Challenge:C generates the common reference string crs and computes the public key h.C then chooses a random bit β and a random c ∈ {0,1}l×2and encrypts c as (v1,v2)=(Enc1(crs;r),Enc2(crs,h,c;r)).Finally,C generates the ciphertext according to β.

• If β=0,then v=(v1,v2).

• If β=1,then it randomly chooses a stringwith the same length as v2and sets v=(v1,).

Then,C sends v to the attacker.

Output:A outputs a guess bit β′for β;if β′=β,then A wins the game.

The blindness property can ensure that the ciphertexts are independent of the public key and the plaintext,which can protect the requester’s privacy.Anyone,even the data owner D,cannot know exactly which part of the data the requester has accessed.

Theorem 2.Our protocol is blind for privacy preservation under the Goldreich-Levin one-time encryption.

Proof.The security definition for the blindness property does not allow any association between the ciphertexts and the public key or the encrypted plaintext.In Step 10 of our protocol,the first part of the ciphertext{gj}is independent of the public key h and the plaintext Miand thus is uniform.From the properties of the Goldreich-Levin one-time encryption,the second part of the ciphertext {{vib}b∈{0,1}}i=γ,···,θis also uniform since the plaintext values Mib(i=γ,···,θ) are uniformly distributed.Thus,any PPT attacker can only win the blindness game with an exact probability of 1/2.

4.3 Security Against Oblivious Requesters

In this protocol,an authorized requester R can only read a small part of the plaintext once at a time t if and only if it obtains an unlocked key for this time t from the file owner F.One security definition in this protocol is proven in terms of chosen-plaintext indistinguishability against oblivious requesters[16,20].

Definition 7.The security against oblivious requesters in our protocol can be defined using the following game between a challenger C and an attacker A.Our protocol should be satisfied such that no PPT attacker can win the following game with a probability≥1/2+1/poly(λ).

Setup:Suppose that the maximum number of rows for a plaintext matrix is n.The attacker A chooses two index numbers γ and θ such that|γ−θ|≪n.For a data owner D,the challenger C computes its public key q and then takes on the role of the file keeper F by setting up the initial masking shardsfor 1 ≤i ≤n.

Update query1:In this phase,A can make queries about the updates of the masking shardsfor each time period,tj.

Token and encapsulated key query:For the time tj,A makes queries about the encryption tokenand the encapsulated keysfor b ∈{0,1}.

Update query2:In this phase,A makes update queries about the encapsulated keys at time tj.Then,A makes queries about either the corresponding unlocked keysfor b ∈{0,1} or the masking shardsfor 1 ≤i ≤n.

Challenge:For each γ ≤ l ≤ θ,A chooses two 2×1 message matrixes Mlb0=and Mlb1=where |Ml00|=|Ml01| and|Ml10|=|Ml11|.Then,A sends Mlb0and Mlb1to C,and C chooses a random bit ω ∈{0,1}and computes the challenge ciphertexts clbωfor b ∈{0,1}and γ ≤l ≤θ.

Update query3:The attacker A can make the same queries as above.

Output:A outputs a guess bit ω′for ω;if ω′=ω,then A wins the game.

Theorem 3.Our protocol is secure against oblivious requesters under the DBDH assumption.

Proof.Suppose an attacker acts as an oblivious requester who wants to access unauthorized plaintext.Then,a challenger C can construct a solution of the DBDH assumption.The game proceeds as follows.

Setup:The challenger C takes g,A=ga,B=gb,C=gc,T as inputs of the DBDH assumption.Then,C randomly chooses µ′,ν′,ui∈Zpfor 1 ≤i ≤n,and it implicitly setsµ=µ′b,ν=,ui=.Then,it publishes the users’public keys as

and the initial masking shards as

Update query 1:In this phase,C answers the update queries of the masking shards.In each time period tj,it randomly chooses a time key∈Zpand computes

Token and encapsulated key query:In this phase,the attacker makes queries on the encryption token and encapsulated keys before creating a ciphertext.The challenger C computes

as the encryption token at time tjand then randomly chooses∈Zpfor b ∈{0,1},which implicitly sets kb=,and computes

as the encapsulated keys at time tj.

Update query 2:In this phase,C answers the update queries of the encapsulated keys at time tj.It randomly chooses∈Zp,which implicitly setsand computes

In this phase,C answers to the queries of the corresponding unlocked keys or the masking shards.For the unlocked keys,it computes

For the masking shards,it computes

Challenge:For each γ ≤l ≤θ,A chooses two 2×1 message matrixes mlb0=and mlb1=where |ml00|=|ml01| and |ml10|=|ml11|.C chooses a random bit ω ∈{0,1} and creates the ciphertexts as

If and only if the input of the DBDH assumption is valid,then

Update query 3:In this phase,C answers the the update queries of the masking shards,the encryption token,the encapsulated keys and the corresponding unlocked keys,as above.

Output:Finally,A outputs a guess bit ω′for ω.If ω′=ω,then C outputs 0 to guess that T=e(g,g)abc;otherwise,it outputs 1 to indicate that T is a random element GT.

In fact,when T is a random element in GT,the messages mlbωare completely hidden from the attacker’s point of view.Thus,C can play the DBDH game with a nonnegligible advantage.

4.4 Security Against Malicious File Keepers

In this protocol,it should be assured that the file keeper F cannot read the plaintext at any time.Thus,one security definition in this protocol is proven in terms of chosen-plaintext indistinguishability against malicious file keepers.There are two scenarios for F to maliciously read the encrypted data content stored on the ledger.The first situation is when F is assumed to take over the role after shard initialization,and the security can be proved using the DBDH assumption.The security proof is almost identical to the proof of Theorem 3 since the masking shards are still initialized by the challenger.In the second scenario,the malicious F is powerful in that it can independently set up the masking shards and freely interact with the requesters.We define only the second scenario as the following game.

Definition 8.Security against a malicious file keeper in our protocol in the second scenario can be defined using the following game between a challenger and an attacker.Our protocol should be satisfied such that no PPT attacker can win the following game with a probability ≥1/2+1/poly(λ).

Setup:Suppose that the maximum number of rows for a plaintext matrix is n.The attacker A chooses two index numbers γ and θ such that|γ −θ|≪n.For a data owner D,the challenger C computes its public key q.However,C does not need to initialize the initial masking shardsfor 1 ≤i ≤n since the attacker A has complete control over them.

Query1:For the time tj,A makes queries on the encryption tokenand the encapsulated keysfor b ∈{0,1}.

Challenge:For each γ ≤ l ≤ θ,A chooses two 2×1 message matrixes Mlb0=and Mlb1=where |Ml00|=|Ml01| and|Ml10|=|Ml11|.Then,A sends Mlb0and Mlb1to C,and C chooses a random bit ω ∈{0,1}.Before computing the challenge ciphertexts,C asks for the updated version of the masking shards.Then,C outputs clbωfor b ∈{0,1}and γ ≤l ≤θ.

Query2:A can make the same queries as above.

Output:A outputs a guess bit ω′for ω;if ω′=ω,then A wins the game.

Theorem 4.Our protocol is secure against malicious file keepers under the IDDH assumption.

Proof.There are three roles in the game.The first role is an attacker,A,acting as a malicious file keeper who wants to decrypt the ciphertexts stored in the ledger.The second role is a simulator,B,who also acts as an attacker to the IDDH assumption.The third role is a challenger,C of the IDDH assumption.The game proceeds as follows.

If and only if the input of the IDDH assumption is valid,then

Finally,A outputs a guess bit ω′for ω.If ω′=ω,then the simulator B outputs 0 to guess that Z=;otherwise,it outputs 1 to indicate that Z is a random element G.

From the above,we can see that if the attacker,who acts as a malicious file keeper,can win the game with a probability of ϵ,then the simulator B can win the IDDH game with a probability of ϵ/2.

V.SECURITY AND PRIVACY ANALYSIS

The above protocol is designed for the security and privacy preservation of sensitive data storage and sharing,which is based on blind batch encryption and the public ledger.The protocol should achieve three security and privacy properties:

1.Anyone,including the data owner and the file keeper,cannot know exactly which parts of the plaintext the requester has read;

2.The file keeper and any outsiders cannot read the plaintext at any time;

3.The requester can read the plaintext only once at time tjon the condition that the data owner sends it an unlocked key for the time tj.

Here,we show the security and privacy-preserving properties of our protocol in the context of four typical attacks on a public ledger system.[21,22]

5.1 Outside Attack

Outside attackers can listen in on the communication channel between the requester and data owner to obtain unauthorized information or alter the ciphertext.The proof of Theorem 1 shows the semantic security of the ciphertext in our protocol.Furthermore,the plaintext has been encrypted using the encryption token and the masking shards cib=for 1 ≤i ≤n,which are generated from the data owner’s public key.Thus,if the outsiders do not know the data owner’s secret key,they cannot decrypt the ciphertext.The outsiders also cannot alter the ciphertext since the file keeper has inserted all the encrypted shards into the public chain.

5.2 Inside Attack

The inside attacker may take the role of a file keeper who reads the plaintext.Theorem 4 has proved that our protocol is secure against malicious file keepers under the IDDH assumption.Thus,the insider acting as a file keeper still cannot read the plaintext.The inside attacker may take the role of an authorized requester at time tjwho wants to access the plaintext at times other than tj.Theorem 3 has proved that our protocol is secure against oblivious requesters under the DBDH assumption.The encapsulated keyis updated for each time period,and the unlocked keycan only be computed for the current encapsulated key.Thus,the requester is only granted a onetime adaptive permission.

5.3 Reuse Attack

If an attacker acts as an authorized requester at time tjand intercepts the communication between the other requester and the data owner at time tj+1to reuse its unlocked keys,this is called a reuse attack.In our protocol,we use the updated masking shardsand the updated encapsulated keysto prevent this attack.If an attacker only has the unlocked key at time tjand wishes to access the ciphertext at time tj+1,it needs to obtain the updated masking shardsand the unlocked key,which is computed from.Obviously,this is impossible.

5.4 Privacy Attack

An attacker may wish to know exactly which parts of the plaintext the requester has accessed,from which it can infer privacy information about the requester.In the worst-case scenario,the attacker may collude with the data owner.In our protocol,we use the blind batch encryption scheme to encrypt the ciphertext matrix vib=gib·cibfor b ∈{0,1}and i=γ,···,θ even if the data owner cannot know the relation between vib,h and cib.The proof of Theorem 2 shows that our protocol is blind under the Goldreich-Levin onetime encryption.From the attacker’s point of view,the encrypted ciphertext vibhas no relationship to the requester’s identity information since vibis independent of the requester’s public key h.On the other hand,vibalso has no relationship to the ciphertexts cib,which provides stronger protection of the cib.

VI.PERFORMANCE ANALYSIS

6.1 Communication Costs of Our Protocol

For achieving 192-bit security as recommended by NIST [23],our protocol over the CDH and DBDH assumptions requires the elliptic curves of 256-bit to 383-bit order.Thus,the length of one element in the group is approximately 383 bits.We first analyze the communication channel between the requester R and the data owner D.Suppose that n ≥104and|δ−θ|=l ≪n.The communication cost in the channel between R and D can be seen the Figure 1.

Second,we analyze the communication channel between the file keeper F and the data owner D.In this channel,D sends all the encrypted shards to F;thus,the communication cost is very heavy,as shown in Table 1.

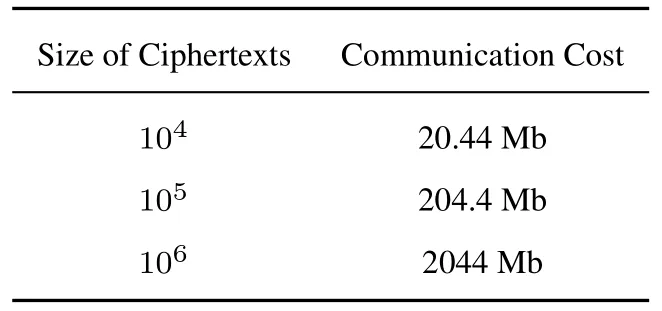
Table 1. Communication cost between F and D.

6.2 Computational Costs of Our Protocol

In this section,we discuss the computational performance of our protocol.We use an Edison platform to simulate the requester R,which is resource-limited with a dual-core,dual-threaded Intel Atom CPU at 500 MHz with 1 GB RAM running Yocto Linux v1.6.In many IoT applications,the requester R is a mobile device,and thus,we implement the prototype of R on the Edison development platform.We use two MacBook Pro platforms with Intel Core i5 CPUs(2.7 GHz)running Os X 10.11.6 with 8 GB RAM to simulate the file keeper F and the data owner D.We implement our protocol in C using the GNU Multiple Precision(GMP) arithmetic library [24] and the pairing-based cryptography(PBC)library[25]for the underlying basic arithmetic and pairing operations.

Suppose that the number of file blocks n ≥104and the number of requested blocks|γ−θ|=l ≤100.We first test the computational costs of R as shown in Figure 2,which carries out the computational operations at Steps 9 and 11 of the protocol.

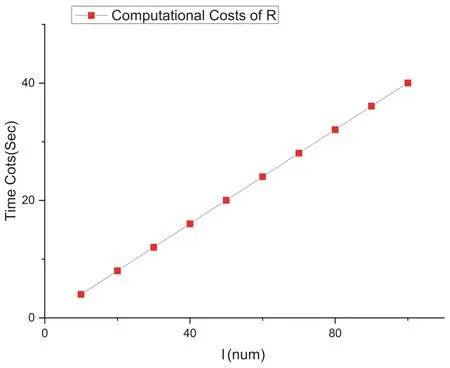
Figure 2. Computational costs of R on the edison platform.

Second,we test the computational costs of F as shown in Figure 3,which carries out the computational operations at Steps 1,2,4,7 and 8 in the protocol.Usually,file keepers are powerful devices for computation and storage;thus,we test it on the MacBook Pro platform.Note that our testing only involves one time period.

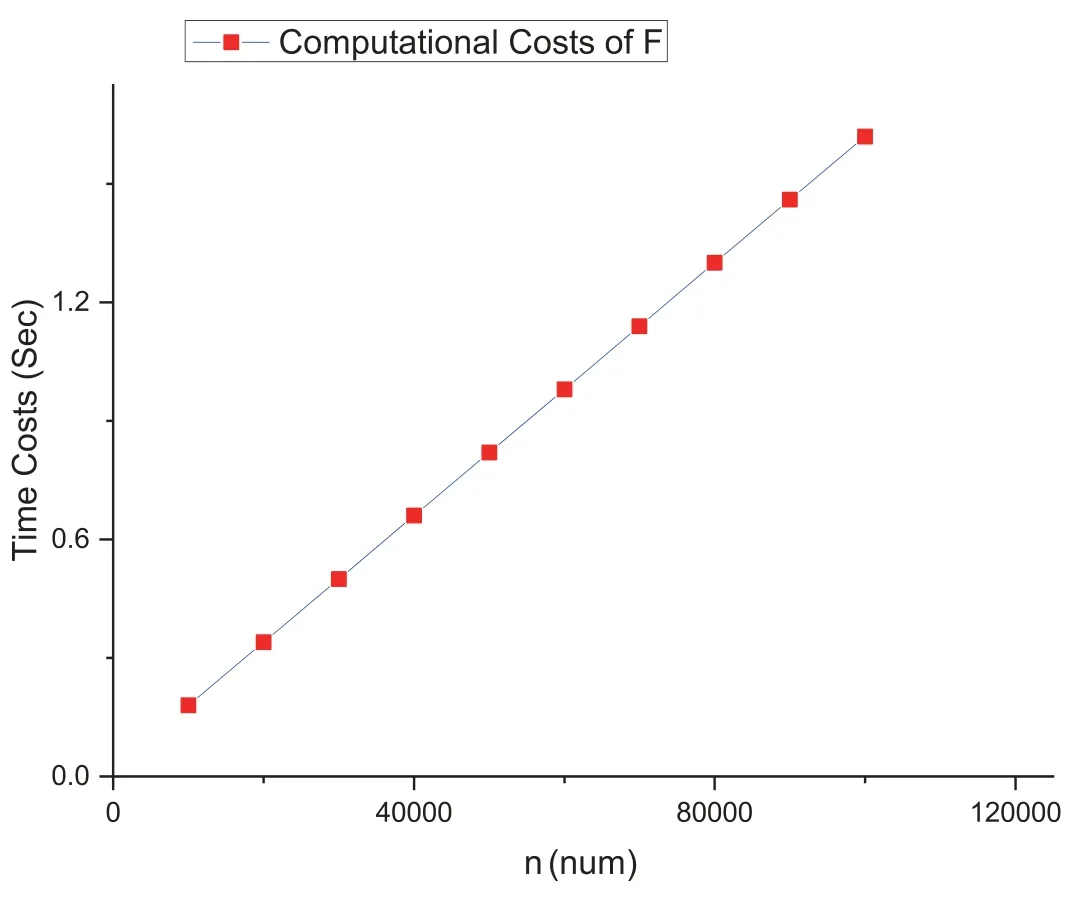
Figure 3. Computational costs of F on the macBook pro platform.

Finally,we test the the computational costs of D as shown in Figure 4,which carries out the computational operations at Steps 3,5,6,9 and 10 in the protocol.Unlike the testing above,the computational costs of D rely not only on the number of l but also on the number of n.We also test in only one time period.

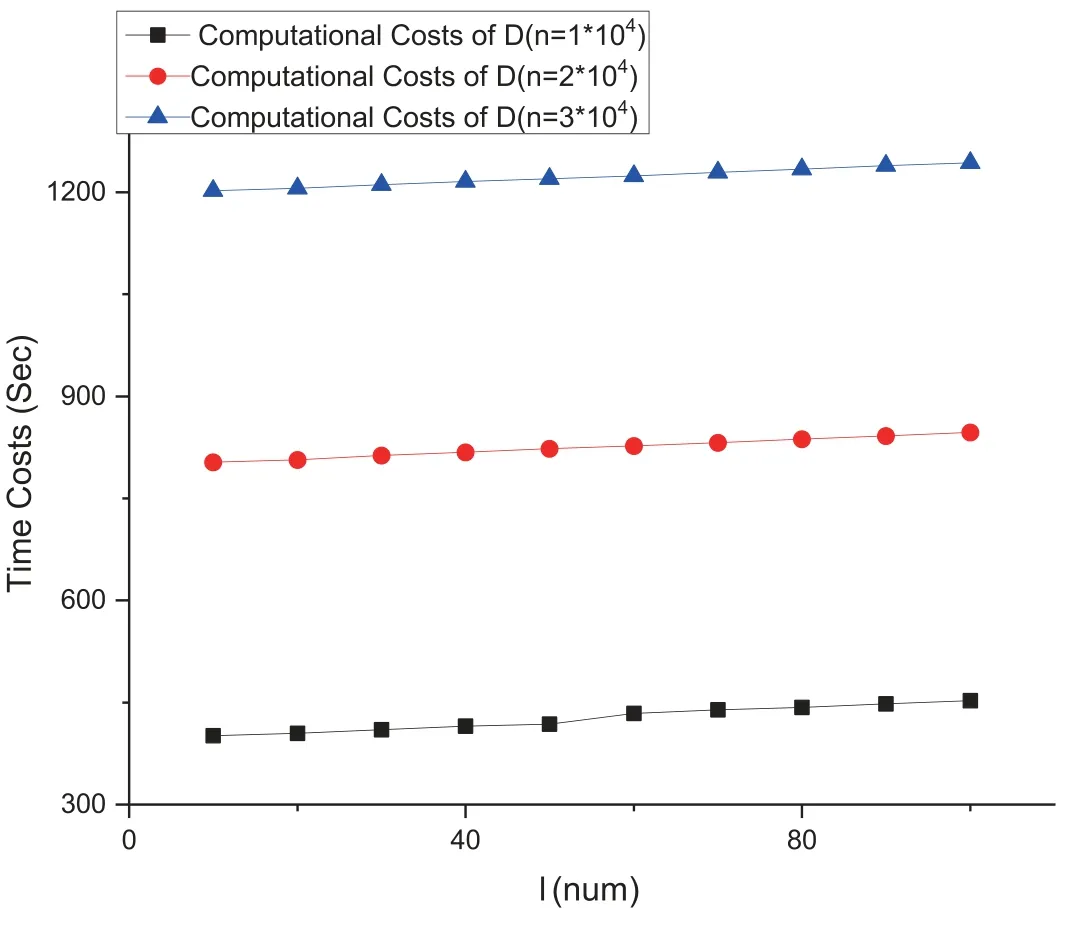
Figure 4. Computational costs of D on the macBook pro platform.

VII.CONCLUSION

Security and privacy concerns are very important in sensitive data sharing for many IoT applications,such as smart health systems.Most data owners want to tightly manage the sharing of their data with one-time adaptive access,which means that the data owner only grants the requester partial access privilege for the fulfillment of the request and that the unlock keys will be revoked after the corresponding time period.In some applications,exactly which parts of the data have been accessed by the requester should also be preserved since this may be related to privacy information.In this paper,we propose a blind batch encryption-and public ledger-based sensitive data sharing protocol.The public ledger can assure the immutability and accountability of the data,and the blind batch encryption can protect the privacy information disclosed by the ciphertexts.The security proofs and analysis of our protocol are also provided in this paper.To test the performance of our protocol,we implement it on the Intel Edison platform and the MacBook Pro platform.

ACKNOWLEDGMENT

This research is partially supported by the National Natural Science Foundation of China under grant no.62372245,the Foundation of Yunnan Key Laboratory of Blockchain Application Technology under Grant 202105AG 070005;in part by the Foundation of State Key Laboratory of Public Big Data;in part by the Foundation of Key Laboratory of Computational Science and Application of Hainan Province under Grant JSKX202202.